基于分形几何的湿式制动器制动噪声分析
2015-06-10罗天洪王云璐罗文军
罗天洪,王云璐,罗文军,林 超
(1.重庆交通大学 机电与汽车工程学院,重庆 400074;2.重庆长安汽车股份有限公司,重庆 400023; 3.重庆大学 机械传动国家重点实验室,重庆 400030)
基于分形几何的湿式制动器制动噪声分析
罗天洪1,王云璐2,罗文军3,林 超3
(1.重庆交通大学 机电与汽车工程学院,重庆 400074;2.重庆长安汽车股份有限公司,重庆 400023; 3.重庆大学 机械传动国家重点实验室,重庆 400030)
湿式制动器的制动噪声产生机理与其摩擦介质的黏滑振动特性有关。为了研究摩擦系数对制动噪声的影响,建立了摩擦系数的分形几何计算模型,将摩擦系数作为变量,分别在忽略与考虑接触斑点的微粒间相互作用时,分析摩擦系数的变化对系统不稳定的影响趋势。在这两种情况下,系统的不稳定趋势完全不同。由此得到了多个参数影响系统的稳定性,在研究湿式制动器制动噪声的时候需要匹配各个参数,使制动系统趋于稳定。
车辆工程;湿式制动器;摩擦系数;分形几何;噪声
0 引 言
湿式多片盘式制动器由于抗污染能力强、制动力矩大、磨损小以及使用寿命长等特点,大量使用于工程机械制动系统中。但装有湿式多盘制动器的车辆在制动开始和结束的时间内,由于摩擦衬片和对偶盘间摩擦系数不是一直不变,而是会发生变化的,使车体产生剧烈振动,并发出低频噪声[1]。
制动器的制动噪声研究虽然已研究了十多年,但制动器噪声仍然是个未解的问题。已经有许多不同的理论提出表面自激振动造成噪声。R.P.Jurvis等[2]最早提出了黏滑现象的不稳定性,负摩擦斜率;F.Massi等[3]采用复杂的固有值分析提出了对噪声预测的数值分析,探究噪声接触表面的摩擦学分析可证实数值结果,接触表面噪声频率局部波动,容易在接触表面产生疲劳,导致发生表层剥落和裂纹;赵文清等[4-6]针对湿式多盘制动器的工作特性,建立了湿式多盘制动器制动时的数学模型,应用模态分析方法研究了其制动噪声产生的机理;付薛洁等[7]对制动器进行了复模态分析,得到了制动过程中产生制动噪声的主要影响因素,并提出了减小制动噪声的改进措施。
综上所述,国内外对制动器噪声的产生机理已经做了非常多的研究,但对于制动器在制动时,表面接触状态的微观变化尚未研究。表面微观状态的改变,对制动器的噪声频率有显著影响。
分形几何作为一种工具用于表征表面结构形态,已越来越受到广泛应用。A.Majumdar等[8]建立了粗糙表面间弹塑性接触的分形模型;F.P.Bowder等[9]采用分形几何方法研究黏着摩擦系数。笔者引入制动器的相关参数,利用分形几何的摩擦系数计算方法,分别在考虑与忽略接触斑点的微粒间的相互作用,对制动噪声进行数值分析,两种情况下结果完全不同。因此,在研究湿式制动器制动噪声需要匹配各个参数,使制动系统趋于稳定。
1 用分形几何描述的摩擦因素
根据摩擦分子机械理论,摩擦表面在载荷作用下的相互作用可分为机械作用和分子作用。分子作用由于分子的活动性和分子力作用使接触微凸体黏附在一起而产生滑动阻力;机械由于微凸体间的相互啮合、碰撞、弹塑性变形和梨沟效应等而阻碍相对滑动。表面间的分子作用力与机械阻力之和的切向分量即为摩擦力。
1.1 摩擦表面接触状态分析
滑动摩擦系数μa被定义为:
(1)
式中:p为液体摩擦副黏性剪切应力;W为摩擦副上作用的法向载荷;Aa为实际接触区域面积。
实际接触区域面积Aa为:
Aa=W/s
(2)
式中:s为法向应力。
表面变形模式主要包括弹、塑性效应,实际总接触面积Aa是弹性接触面积Aae与塑性接触面积Aap之和[10]:
Aa=Aae+Aap
(3)
首先,考虑弹性接触区,Aae为分别弹性接触斑点面积∂上面累加,即:
(4)
式中:n(∂)为摩擦副斑点自身面积分布;∂e2,∂e1分别为在弹性接触区域中最大、最小斑点面积。
在表面接触斑点∂上,选择一种代表性的剪切应力分布,它是接触斑点边缘上的剪切应力:
(5)
式中:W∂e(∂)为作用于弹性接触斑点∂上的法向载荷;v为泊松比。
如果各别弹性接触斑点的泊松比v均一样,将式(5)带入公式(1)则弹性接触区域的摩擦系数μae表示为:
(6)
再考虑塑性接触区域。接触面积Aap同样是各别塑性接触斑点面积∂的累积:
(7)
式中:∂p2,∂p1分别为塑性接触区域中最大、最小的斑点面积。
依据Tabor理论[12],当法向、剪切应力满足如下关系,模型将发生塑性迁移:
(8)
式中:sm为屈服作用力,下文将提到其与屈服应力的关系;γ为实验给定常数,取值位于3~25之间。
将式(8)代入到式(1),从而得到摩擦副塑性接触区域滑动摩擦系数为:
(9)
式中:q为摩擦副塑性接触区域剪切平均应力。
综合以上,系统总滑动摩擦系数μa可表示为:
(10)
式中:W∂p(∂)为作用于塑性接触斑点∂上的法向载荷。
1.2 用分形几何描述的摩擦系数
根据摩擦理论,有如下关系:
(p)∂=μ∂p(s)∂
(11)
将方程(11)带入方程(8),得到
(12)
当接触点处于弹性变形时,接触斑点上的法向弹性载荷W∂e(∂)由Hertizian理论给定:
(13)
式中:E为综合弹性模量;R为摩擦副接触区域斑点微粒顶部的曲率半径。
根据A.Majumdat等[8]的曲率半径表达式
(14)
式中:D为分形维数;G为表面的一种特征长度。
将方程带入得到
(15)
当接触斑点处于弹性变形,则
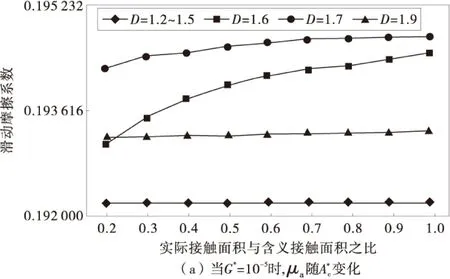
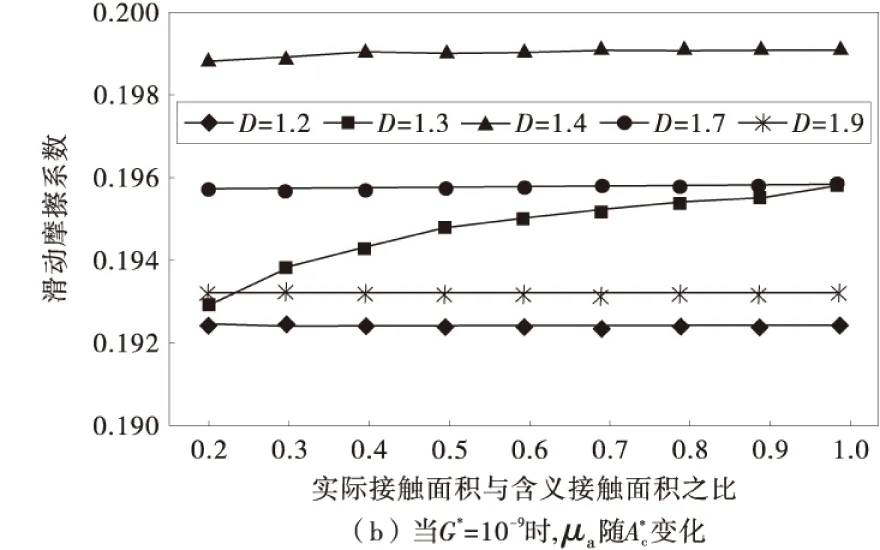
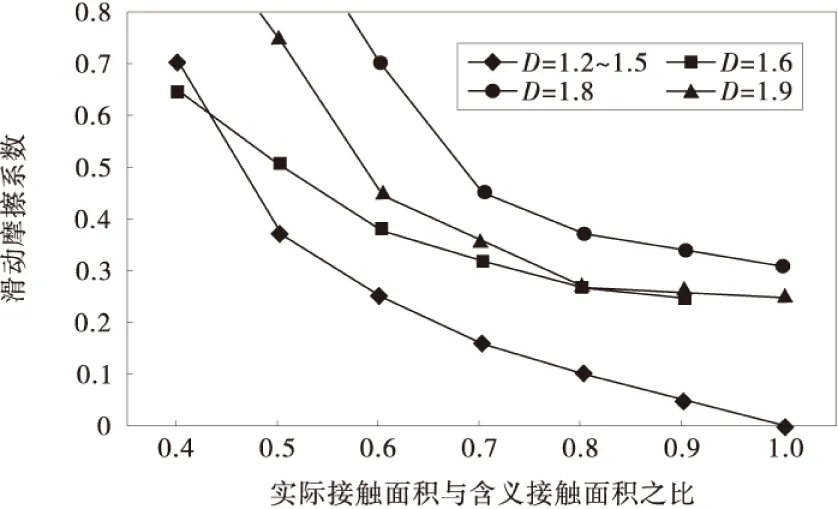
W∂e(∂) (16) 区分弹性与塑性区域的临界面积 ,求出 (17) 如果∂>∂c,接触斑点处于弹性变形状态,接触斑点上的载荷由W∂e(∂)确定。 如果∂<∂c,接触斑点处于塑性变形状态,接触斑点上的载荷为: (18) 因此,总的滑动摩擦系数可以写成 (19) (20) 式中:∂m和∂l分别为最大和最小接触斑点的面积。 接触斑点的面积分布函数n(∂)为: (21) 真实接触面积Ac为: (22) 为便于计算,将(sm)∂,γ∂及μ∂p考虑成不依赖于接触斑点且等于塑性接触区中相应平均值的情况,用如下表达式给出滑动摩擦系数。 μa= (23) 式中: (24) (25) (26) A∂为名义接触面积,载荷We和Wp来自文献[8]。 由于依据Trseca屈服条件,剪切流动应力q具体为: q=0.5δy (27) 式中:δy为拉压条件下屈服应力。 屈服压力sm与应力δy的具体关系表达式为: sm=qδy (28) 对于摩擦衬片的材料为纸基材料,在发生完全塑性变形时: K=2.8~3.0 (29) 根据J.Pullen等[11]研究成果接触斑点微粒间的相互作用,发现屈服压力sm变化存在以下关系: (30) 当最大的接触斑点面积∂m大于临界面积∂c,此时屈服压力sm表示为: (31) (32) 为了研究制动器噪声如何受分形几何参数及归一的接触面积的影响,选取了一些主要计算参数,见表1。 表1 主要计算参数 图1 忽略接触斑点的微粒间的相互作用Fig.1 The interaction between the particles when spots is ignored 因此,在忽略接触斑点微粒间的相互作用,对于每一分形维数,总的摩擦系数随归一面积的增大而增大,系统将更加不稳定。此时如考虑接触斑点微粒之间相互作用关系,对每一分形维数,总摩擦系数随归一接触面积的增大,而急剧减小,系统趋于更加稳定,然而,不能通过单一的1对分形维数及归一接触面积来判定摩擦系数。 采用分形几何的方法研究了制动器在制动时摩擦系数的变化特征,建立利用分形几何推导摩擦系数的方法,通过对各参数特征的数值分析,得到了各重要参数的变化对摩擦系数的影响规律,进而影响系统的不稳定性,得到了以下结论: 1)总的摩擦系数被表示为弹性接触区及塑性接触区中摩擦系数的组合。 2)提出了基于分形几何的摩擦系数求解算法,推导出相应的理论公式,摩擦系数的变化,导致制动噪声的变化明显。 3)对于每一类分形维数,总摩擦系数随归一接触面积的增大而增大,同时增大规律对于不同的分形维数的变化规律也是不同的,当考虑接触斑点微粒间的相互作用时,对于一定的分形维数,模型总体摩擦系数随归一接触面积的增大,呈现明显减少趋势。 4)在不影响制动性能的情况下,对于单纯地降低摩擦衬片和对偶钢盘之间摩擦系数时,需考虑到表面粗糙程度对应最佳分形维数值的关系。 制动噪声是一个复杂的物理行为,许多参数都会影响其发生变化,还包括温度、湿度等参数,在接下来的分析中,将考虑制动时,摩擦表面温度的分形模型,以便更加准确的预测制动噪声的产生。 [1] 管迪华,宿新东.制动振动噪声研究的回顾、发展与评述[J].工程力学,2004,21(4):150-155. Guan Dihua,Su Xindong.An overview on brake vibrations and noise [J].Engineering Mechanics,2004,21(4):150-155. [2] Jarvis R P,Mills B,Jarvis R P,et al.Vibrations induced by dry friction [J].Proceedings of Institution of Mechanical Engineers,1963,178(32):847-857. [3] Massi F,Giannini O.Effect of damping on the propensity of squeal instability:an experimental investigation [J].Journal of the Acoustical Society of America,2008,123(4):2017-2023. [4] 赵文清.湿式多盘制动器制动噪声机理研究[J].中国公路学报,2002,15(4):118-120. Zhao Wenqing.Modeling and restraining study of brake noise on wet multiple brakes [J].China Journal of Highway and Transport,2002,15(4):118-120. [5] 赵文清,盖雨聆.湿式多盘制动器制动噪声建模的研究[J].农业机械学报,2003,34(2):11-13. Zhao Wenqing,Gai Yuling.Modeling of braking noise from wet multiple-disc brakes [J].Transactions of the Chinese Society of Agricultural Machinery,2003,34(2):11-13. [6] 赵文清.湿式多盘制动器制动噪声建模及其噪声抑制的研究[J].兵工学报,2004,25(6):662-665. Zhao Wenqing.Modeling and restraint of braking noise of wet Multi-disc brakes [J].Acta Armamentarii,2004,25(6):662-665. [7] 付薛洁,石博强,姜勇,等.基于ABAQUS的湿式多盘制动器制动噪声研究[J].煤矿机械,2012,33(2):99-101. Fu Xuejie,Shi Boqiang,Jiang Yong,et al.Analysis on wet Multi-disc brake noise based on ABAQUS [J].Coal Mine Machinery,2012,33(2):99-101. [8] Majumdar A,Bhushan B.Role of fractal geometry in roughness characterization and contact mechanics of surfaces [J].Joumal of Tribology,1990,112(2):205-216. [9] Bowden F P,Tabor D.Friction and Lbrication of Solids [M].Oxford:Clarendon Press,1964. [10] 陈大年,陈建平,尹志华,等.粘着摩擦系数的分形几何研究[J].力学学报,2003,35(3):296-301. Chen Da’nian,Chen Jianping,Yin Zhihua,et al.On adhesive friction coefficient with fractal geometry [J].Mechanics Journal,2003,35(3):296-301. [11] Pullen J,Williamson J B P.On the plastic contact of rough surfaces [J].Proceedings of the Royal Society of London Series A,1972,327:159-173. [12] Tabor D.Junction growth in metallic friction:the role of combined stresses and surface contamination [J].Proceedings of the Royal Society of London Series A,1959,251:378-379. Wet Brake Noise Analysis Based on Fractal Geometry Luo Tianhong1, Wang Yunlu2, Luo Wenjun3, Lin Chao3 (1. School of Mechatronics & Automobile Engineering, Chongqing Jiaotong University, Chongqing 400074, China; 2.Chongqing Chang’an Automobile Co.Ltd.,Chongqing 400023, China; 3. The State Key Laboratory of Mechanical Transmission, Chongqing University, Chongqing 400030, China) The generation mechanism of brake noise of wet brakes is related with the stick-slip vibration characteristic of its friction media. In order to study the effect of friction coefficient on the brake noise, the fractal geometry model of friction coefficient was established, regarding the friction coefficient as a variable. The influence trend of friction coefficients change on the instability trend of system was analyzed, when the interaction of particles between contact patterns was ignored or considered. In both cases above, the instability trends of system were completely different. So it is concluded that multiple parameters affect the stability of system. When the brake noise of wet brake is studied, each parameter needs to be consistent with each other, which makes the brake system trend to be stable. vehicle engineering; wet brake; friction coefficient; fractal geometry; brake noise 10.3969/j.issn.1674-0696.2015.05.32 2014-02-01; 2014-04-11 重庆市科学基金重点资助项目(035679);2012年高等学校博士学科点专项科研资助项目(20020183061) 罗天洪(1975—),男,四川乐至人,教授,博士,主要从事工程机械设计、机电液一体化、多领域仿真等方面的研究。E-mail: Tianhong.luo@163.com。 U463.51+2 A 1674-0696(2015)05-160-05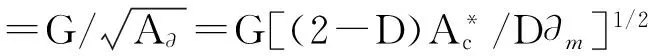
2 分形几何对于湿式制动器制动噪音的效应

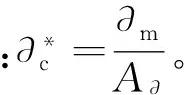

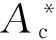
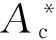

3 结 论
