Mathematica软件在高职数学教学中的应用
2015-06-09牛立尚
牛立尚

摘 要 高职学生数学基础比较薄弱,有些基本的数学概念、定义、定理理解起来非常困难,使得高等数学的授课非常困难,本文将Mathematica①软件应用于教学,除了Mathematica通常的计算和作图功能外,着重强调Mathematica软件在互动性、模型的动态性和教学的交互性上非常符合高职教学要求。
关键词 高职数学 数学软件 Mathematica
中图分类号:G424 文献标识码:ADOI:10.16400/j.cnki.kjdkx.2015.05.052
Application of Mathematica Software in Vocational
College Mathematics Teaching
NIU Lishang
(Fushun Vocational Technology Institute, Fushun, Liaoning 113122)
Abstract Vocational students' math foundation is weak, some basic mathematical concepts, definitions, theorems, it is very difficult to understand, so that is very difficult to teach higher mathematics, this article will Mathematica software used in teaching, in addition to the usual Mathematica calculation and graphing functions, focusing on emphasizes Mathematica software in a dynamic and interactive teaching model of interaction on higher education is consistent with the requirements.
Key words vocational mathematics; mathematics software; Mathematica
Mathematica是当今世界上最流行的数学软件之一,它是美国物理学家Stephen Wolfram领导的小组开发研制,现在成立了Wolfram公司。它功能强大,能解决各种符号计算和数值计算问题,而且能够轻松绘制各种函数图形。
1 Mathematica软件在高职数学教学中的传统应用
1.1 利用Mathematica的计算功能,增强学生计算能力
极限、导数、积分是高等数学中的主要概念和基本运算,传统的教学中我们重在要求学生的笔算能力,但这个过程繁琐无趣,而且在实际中遇到问题时要么是遗忘方法不会算,要么是问题太复杂算不出,而将Mathematica②软件引入教学,轻松几个命令就可快速解决,即使遗忘命令也可以借助帮助功能快速查到。
例如:极限命令Limit[∣]用来计算 ()。
导数命令D[,{}]用来计算 对的阶导数 ()。
积分命令Integrate[]用来计算不定积分。
1.2 利用Mathematica软件的作图功能,完善学生解决问题的手段
例如:绘制由伽马分布生成数据集的一个直方图。
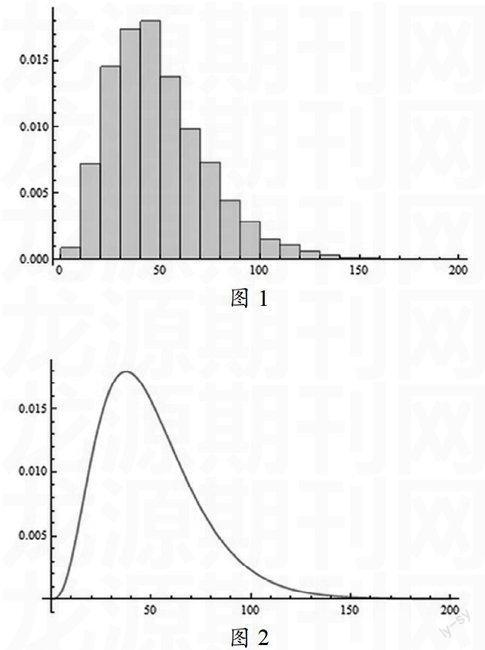
先生成数据集,Mathematica可以由RandomVariate和某种分布来生成抽样的几何,Data=RandomVariate[GammaDistribution[4,12.5],104];再按照此数据集来绘制直方图(图1),这里我们只对概率密度感兴趣,Hist=Histogram[data,Automatic,“ProbabilityDensity”]。
当然我们还可以直接绘制出伽马分布的概率密度函数图形(图2):Pl=Plot[PDF[GammaDistribution[4,2.5],],{,0,200}]
图1
图2
2 Mathematica软件在高职数学教学中的创新应用
高等数学中的一些概念、定义、定理对高职学生来说非常难理解,单单靠画出图形仍不能想象出内在的变化过程,因而仅靠Mathematica的上述应用还是不够的,还要能够动态、互动地呈现一些变化过程。
例如在讲定积分的概念时,我们想用一个实例呈现极限值随着分割的加细而趋向一个定值。
用Mathematica③软件可以计算出sinx函数在0到的区间内的定积分为2,我们还可以动态显示出在这个闭区间内,无论怎样进行取样分割,只要它的子区间长度足够小,函数的积分和都会趋向于一个确定的值。
Manipulate[
Show[
RectangleChart[({}&)/@Sin[Range[0,,/,/]BarSpacing ∣∣,
PlotLabel→NumberForm
[,4]],
Plot[Sin[x],{x,0,}]
],
{n,5,100}
]
在下面的动态模型中(图3),用鼠标操纵滑竿,使得子区间的划分数量不断增大,这时查看sinx在[0,]区间内的积分和是如何逐渐接近积分值2的。
图3
又如,在学习导数定义时,我们先通过一个小实例瞬时速度来引出导数,瞬时速度是很短一段时间内平均速度的极限,即路程对时间的导数。谈到速度,我们很容易想到汽车上显示速度的仪表盘,仪表盘上的数字实时地显示了当前时刻车辆的速度,也就是路程函数的导数,那么我们能不能做一个实例,也像仪表盘一样实时显示函数在某点的导数呢?答案是可以得Mathematica9以上,有一个函数AngularGauge,它可以直接绘制显示某个数值的仪表盘,非常快捷。
先来定义一个函数,然后绘制出它的函数图像和导数图像。④
Fun[x_]:=x^3+2x^2-2;
Plot[{fun[x],fun[x]},{x,-3,3},ImageSize∣ 400,AxesStyle∣ Lighter[Gray],
PlotLegends∣ ”Expressions”,PlotStyle∣ Thick]
运行结果如图4:
这只是一个静态的图像,然后把仪表盘以及函数封装到Manipulate里面,曲线上点的导数就会在仪表盘上显示出来了。
Manipulate[
Row[{AngularGauge[(D[fun[x],{x,1}]/.x∣ p),{-35,35},
GaugeLabels∣ {Placed[“1”Derivative,{.5,.7}],Automatic}],
Plot[fun[t],{t,-4,4},
Epilog∣ {PointSize[Large],Red,Point[{p,fun[p]}]}
ImageSize∣ Medium,AxesStyle∣ ighter[Gray]]}],{{p,-3.5},-4,2}]
运行结果如图5:
图4
图5
这样的讲解,使学生能够轻松地理解概念,这样的动态呈现也更有说服力,学生对这样的课堂教学积极性更高,兴趣更浓。这样的实例还有很多,在此不一一列举。
总之高职数学中引入Mathematica软件,给传统的教学注入了新的活力,学生的学习激情被彻底唤起。我们这些教育工作者要不断学习,挖掘Mathematica软件的更多功能,助力高职教学,为高职教学改革画上炫彩的一笔。
注释
① 丁大正.Mathematica基础与应用[M].北京:电子工业出版社,2013.1.
② 嘉木工作室.Mathematica应用实例教程[M].北京:机械工业出版社,2002.3.
③ 徐安农.Mathematica数学实验[M].北京:电子工业出版社,2004.8.
④ Mathematica实战范例:导数的可视化_百度经验.http://jingyan.baidu.com/article/624e74599ff6df34e9ba5a10.html.
