基于加权BDD的飞行器多阶段任务系统可靠性分析*

范文亮,张永进

(安徽工业大学数理科学与工程学院,安徽马鞍山 243002)

基于加权BDD的飞行器多阶段任务系统可靠性分析*

范文亮,张永进*

(安徽工业大学数理科学与工程学院,安徽马鞍山 243002)

针对不可修的多阶段任务系统可靠性问题,在二元决策图(BDD)方法基础上,提出一种基于加权二值决策图(WBDD)的飞行器飞行任务系统可靠性算法。将飞行器飞行系统视为一个多阶段任务系统,采用任务剖面描述任务时序逻辑关系,考虑系统部件或者产品从完美状态到完全失效的过程中,除了两种状态还存在不完好状态,且能保证阶段的任务完成。利用边扩张构建WBDD,递归遍历WBDD结构,假设部件故障统计独立并计算任务系统的可靠性。通过一个实例,证明此方法的实用性。

多阶段任务系统;加权的二元决策图(WBDD);可靠性

0 引 言

飞行器飞行系统的可靠性直接关系到飞行器的起飞,巡航和降落等阶段任务能否顺利完成。任何一个阶段的失效都会导致整个飞行任务的失败,而且这些阶段之间存在相关性,设备部件在各个阶段也存在相关性。要使得整个任务顺利完成,这就要求整个系统具有较高的可靠性,因此研究多阶段任务系统的可靠性,精确计算系统可靠性具有重要的意义。

关于多阶段任务系统的可靠性分析,采用二元决策图(binary decision diagram,BDD)的思想,它是布尔函数表示的一种图形方式,可以直观地反映出函数的逻辑结构,本身的性质就决定了能完全包含全部不相交路径集(SDP),与其他方法相比具有占用空间小,计算效率高特点[1-3]。根据各阶段故障树得到每个阶段的BDD,对各阶段的二值决策图(BDD)也进行组合分析[4]。最后阶段代数来处理阶段间的依赖性,获得系统BDD。针对任意一个排序系统BDD,构造算法——两阶段算法[5-6]。然后采用 Zang Xinyu和Mo Yuchang[7-8]提出的算法对系统中的设备单元进行排序生成单阶段BDD,最后生成系统BDD计算可靠性。此外包含多状态失效的多阶段任务系统问题,基于二元决策图的相依失效分析方法[9-13]具有较高的效率。

然而,这些多阶段可靠性研究一般假设部件故障统计独立,且仅考虑处于多个阶段间及在同一阶段的相关性。飞行器飞行工作处于长期工作和恶劣环境中,会导致设备部件不仅仅只有两种状态(完美和失效),还会处于不同性能水平状态。事实上满足:①当组成系统的二态元件对系统性能影响具有累计效应;②当组成系统元件随着时间而发生恶化(疲劳,局部故障)或者外部环境的变化而导致元件性能下降。统称为多状态系统(MSS)。这里用“带伤工作”部件为统称来代替处于除完美和失效外的一切状态。综合考虑这种复杂的相关性和多态性,建立多状态BDD的可靠性模型。提出一种基于加权BDD的飞行器多阶段任务系统可靠性算法。

1 飞行器飞行任务系统可靠性模型

本文研究飞行器飞行任务可靠性,即规定时间内飞行任务在多个阶段之间成功完成的概率。不完好状态性是设备元件的性能随着阶段的进行,各设备出现磨损,消耗或不同程度的破损,使得出现各种不同性能的状态,但又能保证系统任务的完成。

对飞行器飞行任务可靠性分析基于三个假设条件:

(1)系统具有不可修复性:系统完成结束之前,在某阶段失效,系统无法完成。

(2)设备单元失效具有独立统计性,且失效率寿命服从指数分布。

(3)每个阶段持续工作时间不受系统状态影响。

飞行器飞行可以看成多阶段任务系统,分为上升,巡航和着陆(返回)等阶段,在每个任务阶段里,需要不同的设备单元来完成不同需求的阶段任务。有可能一个设备元件在所有阶段都参与工作,也有可能一个设备元件仅在某一阶段工作。

假设某飞行器所进行的飞行任务由0时刻开始, t3时刻结束,期间需要系统的设备单元A,B,C,D,E, F,G,H提供业务情况。如图1所示。

图1 飞行器设备工作时序图

在时间[0,t1]段,设备A,D必须正常工作,B,C至少有一个正常工作,才能保证该阶段任务完成;在[t1,t2]段,设备A,F,G必须正常工作,B,E至少有一个正常工作,才能保证该阶段任务完成。在[t2,t3]段,设备A,D,H都正常工作,才能使得该阶段任务完成。只有三个阶段都正常工作才能使得整个飞行任务系统的完成。飞行器各设备如表1所示。

表1 各设备对应编号

考虑同一部件不仅仅只有两种状态(完美和失效),还会处于不同性能水平状态。每个设备分别处于三种不同状态为:

其中:pi1+pi2+pi3=1,i=A,B,C,D,E,F,G,H。

在各设备失效的独立统计性基础上,假设设备失效时间服从指数分布,且彼此相互独立,则上述时序逻辑关系转化成任务剖面表见图2,进而建立飞行器飞行任务PMS模型。

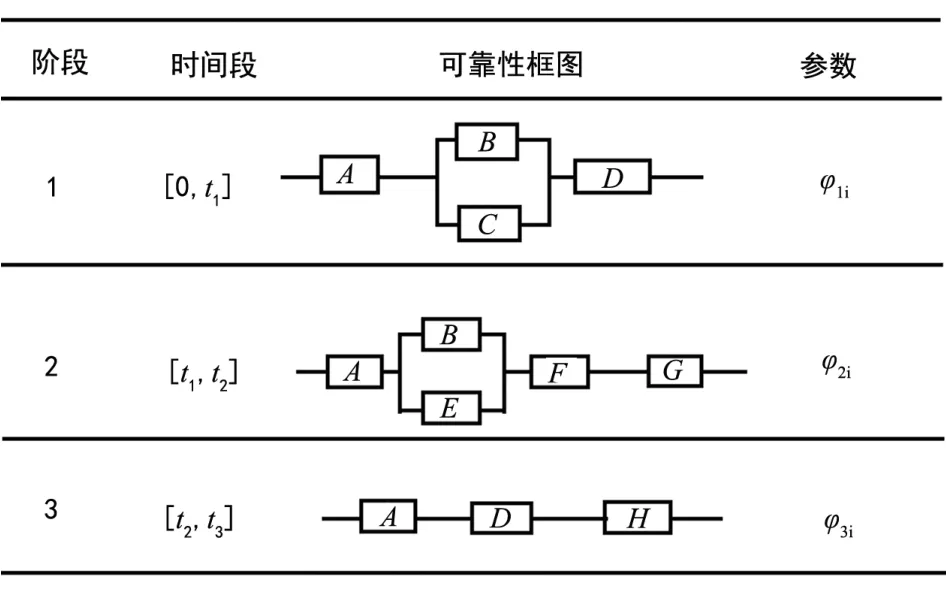
图2 任务剖面图

图2中,在第k个时间段中设备i的失效率参数,用φki表示。

2 WBDD建立

2.1 WBDD

BDD是一种对布尔函数进行表示和操作的高效方法,是一种有向无环图。WBDD对BDD附加了约束条件,是布尔表达式的一种规范型。考虑同一部件不仅仅只有两种状态(完好和失效),还会处于不同性能水平状态。通过用“带伤工作”单元的状态概率进行加权由系统建模,分析并得到PMS的数据后,再进行可靠性分析,得到基本流程见图3。

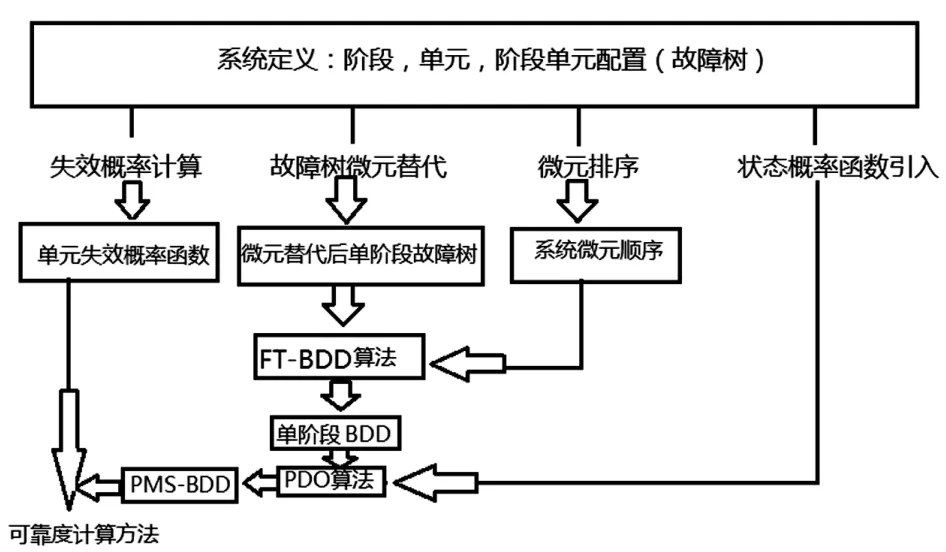
图3 算法PMS-WBDD的流程图

主要由以下步骤:微元替代与排序,失效概率函数计算,状态概率函数的引入,单阶段BDD构建,系统加权BDD构建和系统可靠性计算。

2.2 阶段间相关性处理

解决各阶段之间相同设备单元的相关性。采用Esary J D提出的微元替代和阶段代数的方法。例如,在PMS的各个阶段中,用和阶段所需要的相同微元Ai(1,2,3...)来代替设备单元A,然后运用阶段代数来处理同一设备单元的不同微元之间的关联性(见图4)。因此,微元置换PMS中故障树,可得到对应微元替代的阶段故障树。最后构建阶段BDD。

图4 微部件思想

其中:A1A2...An为设备A的相同微元,设备元件在阶段k失效。

通过对系统中各微元进行排序,得到单阶段的BDD。Mo Yuchang分为两个步骤对微元排序:系统微元和替代微元排序。在系统故障树的基础上对系统单元排序,飞行器飞行任务系统的成功必须要求各设备单元在相应阶段顺利完成规定任务。否则只要有一个阶段失败,则系统飞行任务失败。因此系统故障树就是各阶段的故障树并联。

由阶段的并联特性,可对各微元进行排序得到规模较小的BDD,需要采用后向PDO排序算法,它是由Zang Xinyu所提出的。此算法按照系统单元的顺序将每一设备单元的替代微元按照阶段从后至前的顺序排列在一起。例如,在PMS中,由所有的阶段故障树所组成的系统故障树排序,得到的结果为A＜B＜...＜H,然后运用后向PDO排序算法对单元在各阶段的替代微元进行排序结果为:

A2＜A1＜B2＜B1＜...＜H2＜H1

式中:Ai,Bi,...,Hi(i=1,2)为设备单元各阶段替代微元。

2.3 失效概率函数计算

当各阶段的设备单元失效概率,随时间的变化,我们称为失效概率函数。通过阶段代数可知,单元的失效概率不仅受单元所在当前阶段影响,而且与之前阶段的替代微元的失效率也有关系。不防设单元的失效率服从指数分布,由指数分布的无记忆性,即设备单元工作时间t后,寿命与已工作的时间长短无关。则各阶段设备单元的替代微元失效概率函数为:

这里,阶段i持续时间长度用t来表示;设备单元在阶段i的失效率用λi来表示。

然后得到设备单元的概率失效函数计算表达式:

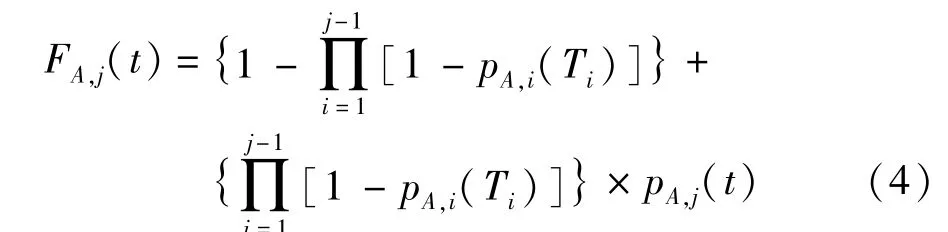
式中:第i(i≥j)阶段的时间长度为Ti。式(4)的前部分表示设备单元A在阶段j之前失效概率,后部分表示设备单元A在阶段j阶段失效概率。

2.4 单阶段的BDD

为得到单阶段BDD,通常采用至上而下,至左到右依次遍历各个阶段故障树方法,对基本事件变量进行排序。由于BDD是对布尔函数进行图形化表达和操作的一种方法,通常用BDD的操作来表示逻辑运算。在实际操作中,BDD的构造通常采用逻辑运算而不直接采用香农分解;另外还有成分组合法。这里我们运用递归思想进行ite构造方法。假设布尔函数表达式的香农展开:

这里任何一个逻辑运算符用Δ表示。

对布尔代数表达式g和h的子表达式G1,G2,H1和H2用相同规则进行递归操作,当表达式出现常数值1或0为止。最后得到故障树所对应的BDD。

2.5 系统BDD和加权BDD构建

引入微元替代以及阶段代数,目的是解决阶段间的依赖性。在处理阶段代数关系时,我们采用阶段依赖性运算 PDO排序算法,由 Zang Xinyu和 Mo Yuchang提出。根据PDO依赖变量顺序的特点,可分为两类:

①前向PDO:变量的编号排序相似于 A1,A2, A3...,An

②后向PDO:变量的编号排序相似于An,An-1,An-2...,A1

要得到系统的BDD,根据PMS的特点,需选择运用合适阶段依赖性算法。依次对各阶段BDD进行运算并进行加权状态概率函数。最后得到系统相应的加权BDD。

3 系统可靠度计算

根据生成的系统二值决策图计算不可维修的多阶段任务系统的可靠性,需要考虑跨阶段依赖性,因此可靠性计算分三步进行:

(1)由式(3)、(4)计算各设备元件在各阶段的失效率和可靠度。

(2)计算各二值决策图中结点的可靠度。

(3)通过加权后二值决策图,按照自底向上搜索出从终结点“0”到根结点的各条路径。各路径的概率为路径中结点的可靠度之积。各条路径的可靠度之和为系统的可靠性。

在Zang Xinyu的分析上知,不同设备单元的两个微元总是连接系统BDD“0”的两边,而连接系统BDD“1”边的两个微元不一定属于相同的设备单元。

p(Fm),p(Fn)为对应的单阶段BDD可靠度,n= 1,2,3,...N为设备元件个数。其中有k个设备元件“带伤工作”,对应的Pr{Xn=ζ}为“带伤工作”状态概率函数。有N-k个设备元件“完好工作”,对应的Pr {Xn=σ}为“完好工作”状态概率函数。一方面对式(10)～(13)进行递归运算,另一方面运用式(14)对各个设备单元进行加权,得到系统BDD的可靠度。

4 算例分析

结合飞行器飞行任务系统模型和表1,假设飞机各设备元件的失效率服从指数分布。A,C,D设备元件平均无故障时间166 h,E,F,H设备元件平均无故障时间666 h,B,G设备元件平均无故障时间分别为333和500 h。由指数分布特点得到相应的失效率及式(1)和(2)得到状态概率函数如表2,各设备元件在飞行起飞阶段到爬升结束的持续时间为10 min,巡航阶段为30～300 min,降落阶段持续时间需用20 min。

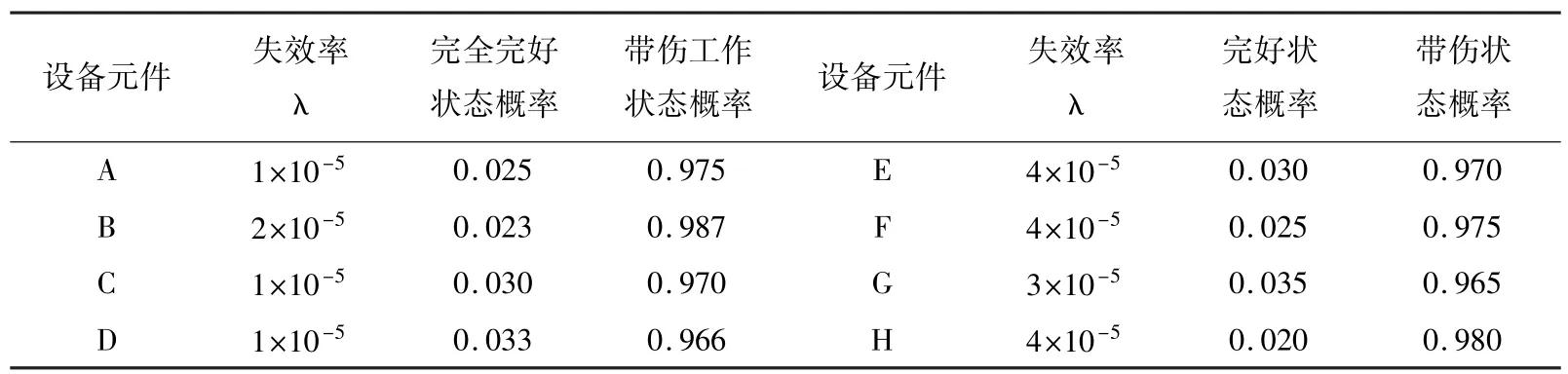
表2 设备元件参数

通过2.2节的微元替代和排序方法,并对设备单 元进行逻辑结构运算。得到对应的PMS故障树。再由任务剖面的可靠性框图(见图2),依次建立各阶段故障树(见图5)。其设备单元A故障用A-=1表示。

图5 任务阶段故障树

先对系统故障树进行排序得到:A＜B＜...＜H,然后运用后向PDO排序算法对各阶段的替代微元单元进行排序,进而得到系统中的微元排序:

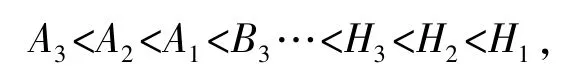
最后通过2.3节中的方法,对微元替代后的各阶段故障树分别构建各阶段相应BDD,如图6所示。这里=1和=0分别代表设备单元A在阶段j故障和正常。为得到系统BDD见图7,运用2.4节后向PDO排序算法,依次对各阶段的BDD进行逻辑运算。

图6 单阶段的BDD

图7 系统BDD

由2.2节计算失效概率函数方法,得各阶段末,系统所有测控单元可靠度为:

最后运用2.5的方法,对图7所示的系统BDD进行递归和加权求解,得到系统在巡航时间30 min的可靠性为Rs′=0.9818。不加权的系统BDD可靠性Rs=0.9964。两者相比可知加权后的系统可靠性更具合理性。

5 结 语

综合考虑系统单元在阶段之间的依赖性以及多模式失效的依赖性,建立了飞行器多阶段飞行任务系统可靠性模型,进一步对得到的系统BDD进行加权,

通过遍历BDD结构综合分析多阶段任务系统可靠性,给出求解方法。避免过程的重复计算,且加权计算只需创建和保存一个系统BDD结构,节省计算时间和存储空间。

[1] X.Zang,D.Wang,H.Sun,et al.A BDD-Based Algorithm for Analysis of Multi-state Systems with Multi-state Components[J]. IEEE Trans.Computers,2003,52(12):1608-1618.

[2] 张 涛,郭 波.一种基于BDD的多阶段任务系统可靠度新算法[J].系统工程与电子技术,2005,27(3):446-470.

[3] Guangyu Chen,Xizi Huang,Xiaowo Tang.A BDD&SEA based analysis of generalized phased-mission reliability[J].Reliability and Maintainability Symposium,2006(3):456-463.

[4] Zhihua Tang,Joanne Bechta Dugan.BDD-Based Reliability Analysis of Phased-Mission Systems With Multi-mode Failures[J]. IEEE trans.on Reliability,2006,55(2):350-360.

[5] Zang Xingyu,Sun H,Trivedi K S.A BDD-based Algorithm for Reliability Analysis of Phased-mission Systems[J].IEEE Trans.on Reliability,1999,48(3):50-60.

[6] 段 珊.二元决策图排序的排序优化及故障树转化方法的研究[D].长沙:中南大学,2008.

[7] 曾令国,莫毓昌.PMS故障树分析中的变量排序策略库研究[J].计算机工程,2011,37(20):39-41.

[8] Xing Liudong,Dugan J B.Comments on PMS BDD Generation in A BDD-based Algorithm for Reliability Analysis of Phased-mission System[J].IEEE Trans.on Reliability,2004,53(2):169-173.

[9] Mo Yuchang.New Insights into the BDD-Based Reliability Analysis of System[J].IEEE Trans.Reliability,2009,58(4):667-678.

[10] Tang Z,Dugan J B.BDD-based reliability analysis of phasedmission systems with Multi-mode failures[J].IEEE Trans.Reliability,2006,55(2):350-360.

[11] L.Xing,Y.Dai.A new decision diagram based method for efficient analysis on Multi-state Systems[J].IEEE Trans.Dependable and Secure computing,2009,6(3):161-174.

[12] 陈 瑶,李 峭,等.基于OBDD的航空电子网络可靠性分析[J].系统工程与电子技术,2013,35(1):230-236.

[13] 罗 航,廖俊必,等.实现最优BDD结构的联合改进方法[J].电子科技大学学报,2012,41(1):48-53.

Reliability Analysis of Aircraft Phased-Mission System Based on the Weighted BDD

FAN Wen-liang,Zhang Yong-jin
(School of Mathematical Science and Engineering,Anhui University of Technology,Maanshan Anhui 243002,China)

In terms of reliability problems for the immutable multi-phased mission system,aircraft flight mission reliability analysis model and the algorithm are proposed based on the binary decision diagram(BDD)method and weighted binary decision diagram(WBDD).Regarding aircraft flight system as a multi-stage task system,this mission profile table is adopted to describe the logical relationship of task and order,consider that there is incomplete state in addition to the two kinds of state in the process from the perfect state to complete failure of the system components or products,and guarantee the phase of the task to complete.Weighted binary decision diagram is proposed afterward,and the reliability of task system is calculated with assumption that the statistic of components failure is independent.Finally,the effectiveness of the proposed method is verified by a numerical example.

phased-mission system(PMS);weighted binary decision diagram(WBDD);reliability

TB114.3

A

1007-4414(2015)05-0064-05

10.16576/j.cnki.1007-4414.2015.05.021

2015-07-07

国家自然科学基金项目(编号:70971064)

范文亮(1986-),男,河南安阳人,硕士,主要从事可靠性优化与算法方面的研究。

张永进(1976-),男,博士,副教授,主要从事机械可靠性设计方面的研究。