舰炮身管的对流换热系数热化学计算方法*
2015-06-09任华杰周传晟胡景豫
任华杰,周传晟,胡景豫
(海军驻齐齐哈尔地区军代室,黑龙江齐齐哈尔 161000)
舰炮身管的对流换热系数热化学计算方法*
任华杰,周传晟,胡景豫
(海军驻齐齐哈尔地区军代室,黑龙江齐齐哈尔 161000)
火炮射击身管处于高温高压时,通过有限元热化学分析方法,输入参数,来获得对流换热系数的值。在沿火炮身管轴线方向,通过考虑火药燃烧速度、压力波速度、密度、燃烧气体混合物的热传导率的变化来评估雷诺兹和普朗特系数。这两个数值被用来计算努塞尔系数以确定不断变化的对流换热系数。它通过模拟发射过程和其相应的热化学有限元分析方法确定了这个系数,较好的反应了数值的真实性。
身管;对流换热;热机械;热化学
0 引 言
火炮身管是暴露在高动态载荷和高热输入下,会导致在射击过程中温度急剧升高,这些输入的来源是炮弹火药燃烧产生的热应力。火药燃烧一般认为有三个阶段:第一阶段,火药开始在定容条件下燃烧直到推动炮弹开始运动;第二阶段,火药继续燃烧直到推动炮弹到达炮口;第三阶段,炮弹刚刚离开火炮身管在大气条件下燃烧。在炮弹动态的复杂热化学过程下的热性能需要火炮身管建模和计算机辅助分析才能确定。
火炮身管热分析的实验方法在许多文献中都有涉及,如“反求法”和“函数估计方法”这类分析研究,在试图确定热通量和温度迭代的时候也存在需要提前测定温度的缺点[1-2],直接的分析方法也由于复杂的时间依赖性也只能有限发展[3-4]。
从以上描述可以推断,在热态机械的热烤温度设计阶段,通过火炮身管壁传递热量的多少是非常必要且重要的信息。火药燃烧的混合气体与身管内壁的对流换热量直接依赖于传热系数。笔者旨在通过遵守身管内热量流动方向规律的一个新的热化学方法来确定传热系数。本实验基于美军MK75型舰炮,口径76 mm,身管长度4 712 mm,初速1 120 m/s,最大发射率85 r/min。
1 身管内压力和速度的变化
想计算该传热系数必须做假设,放热燃烧率假设为线性,燃烧混合气体假设为理想气体,混合气体压缩比KC=1.34[5],火炮身管内膛直径 D= 76 mm。压力和速度随时间和身管轴线方向的变化如图1、2。
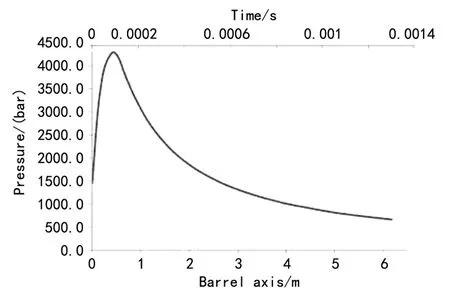
图1 身管内压力图
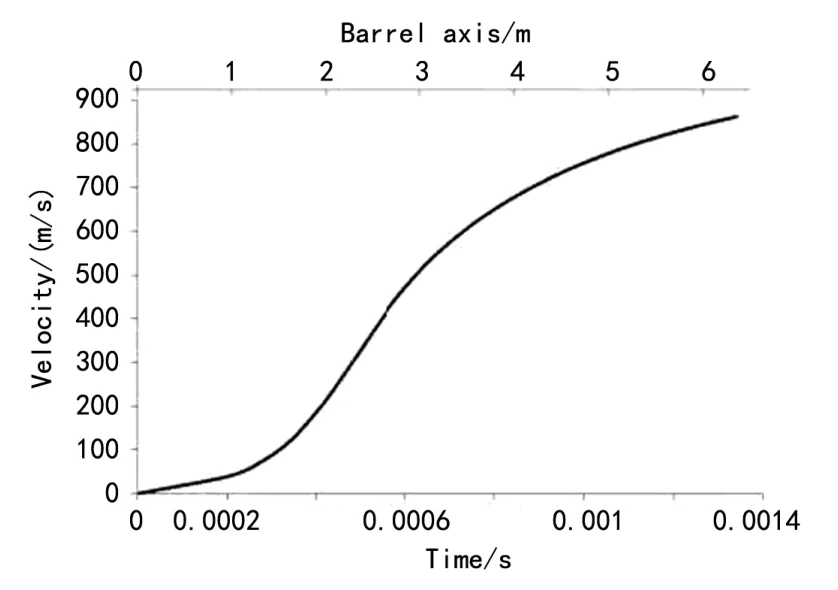
图2 炮弹速度
2 炮弹脉冲气体成份和化学反应
硝化棉和硝化甘油燃烧产生脉冲混合气体,化学反应方程式如下:

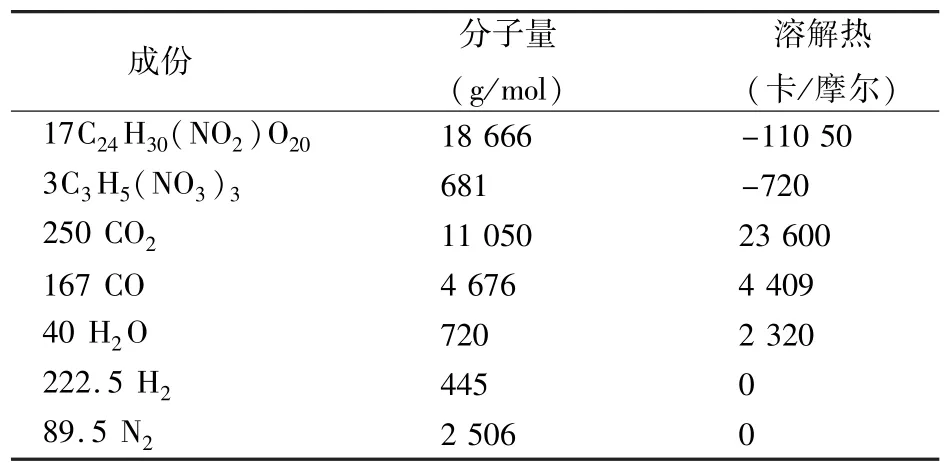
表1 反应物化学成份
3 气体混合物与身管内表面的对流换热系数
3.1 大气条件下的混合气体
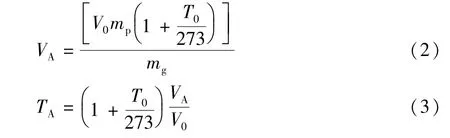
当火药在大气条件下燃烧时可以计算出混合气体的体积VA、温度TA分别根据下面的理想气体定律得出:式中:mp表示混合气体摩尔数;T0表示室温(20℃);V0表示每摩尔气体混合物体积为22.4 L;mg表示物质反应后摩尔数。利用这些方程,这些物质燃烧后计算出VA为956 L,TA为797℃。
3.2 身管内混合气体温度的计算
计算混合气体沿身管轴线方向温度Tb可将式(3)~(4)中计算出的结果带入式(4):
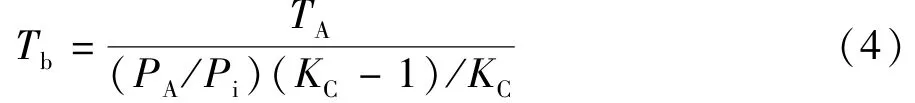
式中:Pi表示沿身管轴线方向身管内压力的变化值, KC代表恒定压缩比,Tb由式(4)计算得出,绘制出曲线如图3所示。
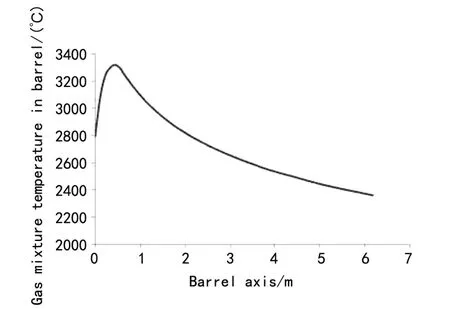
图3 气体混合物沿身管轴线方向温度变化曲线
3.3 混合气体雷诺兹数的计算
下面的等式定义了沿身管方向混合气体的雷诺兹数计算公式,其中直径d为76 mm。

式中:0.000 2≤c≤0.000 86,0.6≤n≤0.86。根据火药的成分即85%的纤维素和15%硝基甘油,得出式(8)和式(9)的值为0.000 548和0.775。随着vg的增加,c和n分别达到0. 000 86和0.86,ρ、μm、vg随身管轴线方向的数值曲线如图4~6,应用这些数值,根据式(5)得出雷诺兹数曲线,如图7所示。
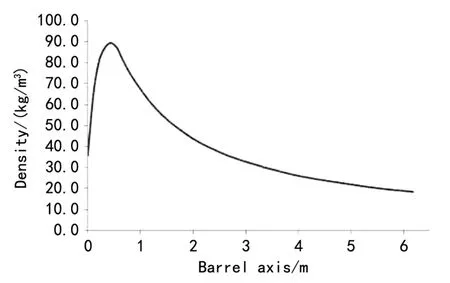
图4 混合气体密度随轴线方向变化曲线
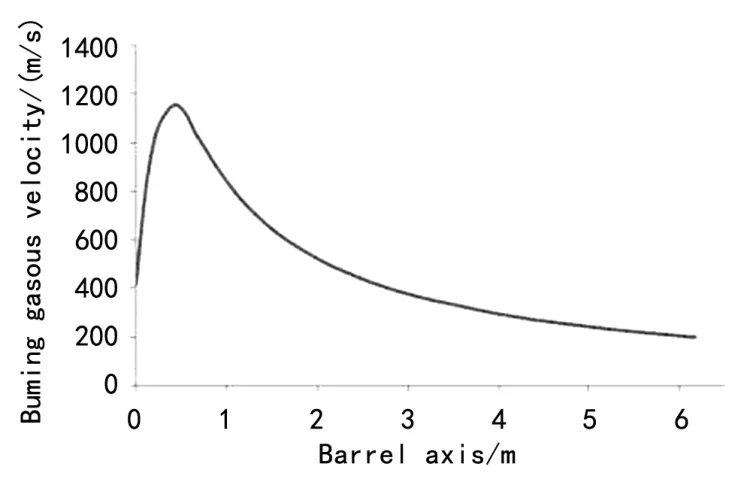
图5 混合气体随轴线方向膨胀速度变化曲线
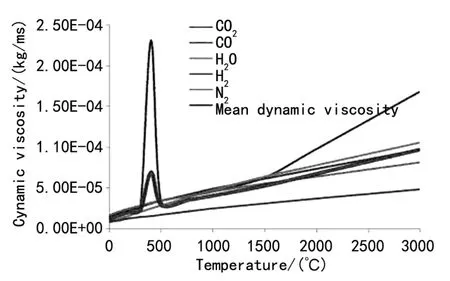
图6 混合气体随温度变化的动力粘度曲线
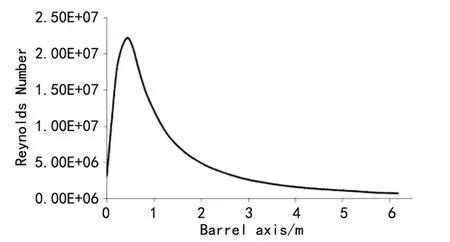
图7 混合气体雷诺兹数随身管轴线方向变化曲线
3.4 混合气体平均普朗特数的计算
醋酸阿比特龙为一种针对雄激素的生物合成抑制剂,在体内被转化为阿比特龙,可以特异性抑制17α-羟化酶/C17,20-裂 解 酶(cytochrome P450 17α-hydroxylase/17,20-lyase,CYP17)的活性,从而减少肾上腺和肿瘤中雄激素的合成。阿比特龙的作用依赖于AR,适用于与泼尼松联用,治疗既往接受含多烯紫杉醇化疗的转移去势难治性前列腺癌患者。由此提示,使用醋酸阿比特龙可以减少雄激素的生成,从而提升针对AR阳性乳腺癌患者的药物疗效。
根据反应式(1),随温度变化的每种反应物的普朗特数根据参考文献[5]、[6]得出。应用这些数值,计算出混合气体的平均普朗特数,如图8所示。
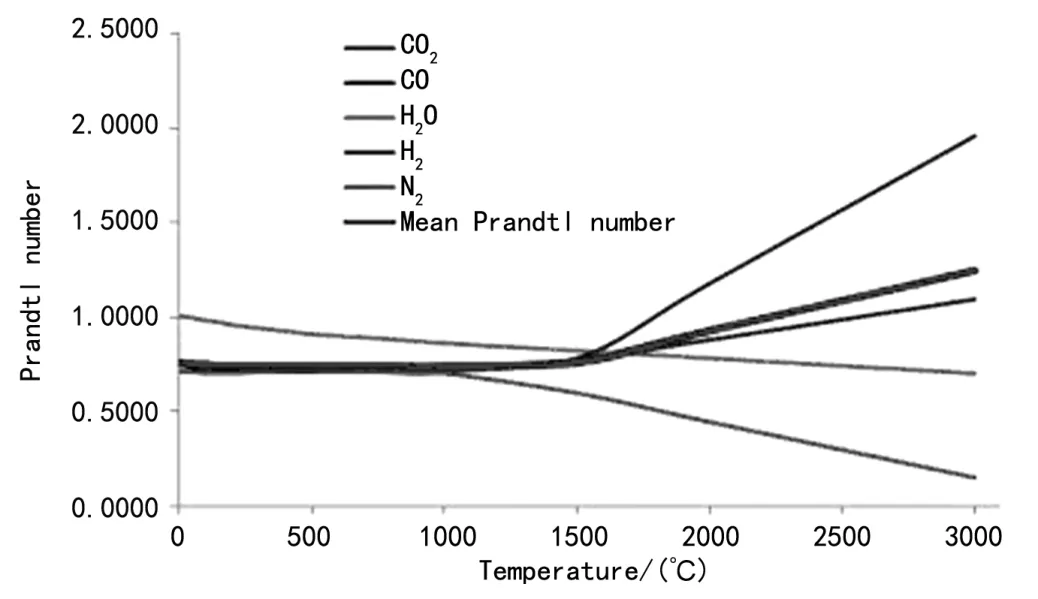
图8 身管内混合气体的平均普朗特数
3.5 混合气体努赛尔数计算
根据参考文献[5]、[6],努赛尔数计算根据式(10)得出:

式中:Re>>10000,L/D≥10。
3.6 身管内混合气体传热系数计算
沿着身管轴线的对流换热系数h由据式(11)得出:

式中:对流换热系数h的曲线如图11,其中混合气体的努赛尔数Nu、热传导系数k的曲线如图9、10。
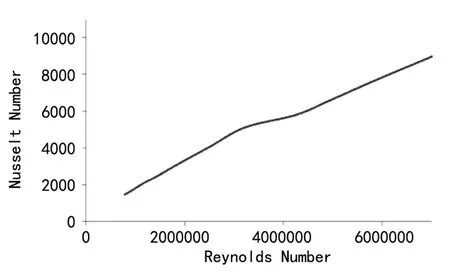
图9 身管内混合气体的努赛尔数曲线
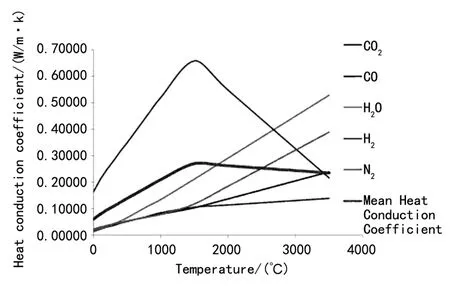
图10 身管内混合气体的平均热传导系数曲线
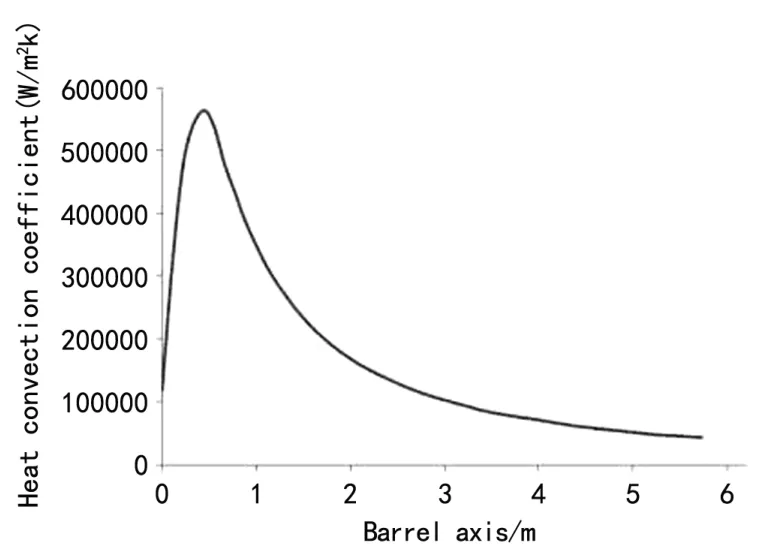
图11 身管内混合气体的对流换热系数曲线
4 试验结果和结论
为了验证计算的混合气体对流换热系数的有效性,对身管温度进行了测量,也建立了ABAQUS热机械有限元模型如图12,图13为计算和测量的身管表面温度图。

图12 身管内ABAQUS热机械有限元模型
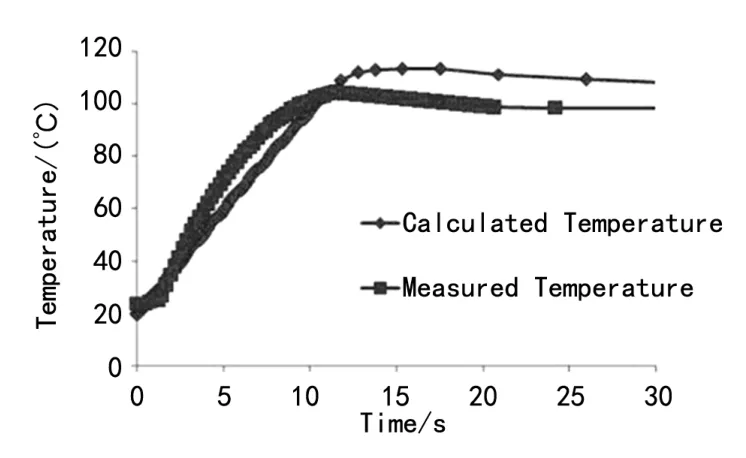
图13 计算和测量的身管表面温度
应用三热激光传感器对身管表面温度进行10 s的测量,并进行1.3s左右的连续拍摄,得出在相同条件下射击时两种方法身管内温度达到最大值的位置,这种方法使得比较外表面的计算温度和实际温度有了可能,结果如图13。
由图12、13可知,计算和测量的外表面温度几乎遵循相同的趋势,它们之间最大差异为8%,这表明所开发的热化学方法对射击时身管内对流换热系数的计算具有有效性。
[1] T.C.Chen,C.C.Liu,H.Y.Jang,P.C.Tuan.Inverse Estimation of Heat Flux and Temperature in Multi-layer Gun Barrels[J]. Heat Mass Transfer,2007(50):2060-2068.
[2] Y.Hwang,S.Deng.Applying Neural Networks to the Solution of the inverse Heat Conduction Problem in a Gun Barrel[M].Vessel Technol Press,2008.
[3] S.Singh,P.K.Jain,Rizwan-uddin.Analytical Solution to Transient Heat Conduction in Polar Coordinates with Multiple Layers in Radial Direction[J].Thermal Sci,2008(47):261-273.
[4] S.Jaramaz,D.Mickovie,P.Elek.Two-phase flows in gun barrel: theoretical and experimental studies[J].Multiphase Flow,2011 (37):475-487.
[5] Y.A.Cengel.Heat Transfer:A Practical Approach[M].McGraw-Hill Press,2003.
[6] F.M.White.Fluid Mechanics[M].McGraw-Hill Press,2003.
A Thermo-chemical Approach for Calculation of Convection Heat Transfer Coefficients in Naval Gun Barrel
REN Hua-jie,ZHOU Chuan-sheng,HU Jing-yu
(Navy Representative Office in Qiqihaer,Qiqihaer Heilongjiang 161000,China)
A finite element thermo-mechanical analysis of firing through a gun barrel requires the convection heat transfer coefficient values under high temperature and pressure among input parameters.Considering the variable burning speed for a typical gunpowder configuration,the variation of pressure wave speed,density,and heat conduction of the burning gas mixture are used to evaluate the Reynolds and Prandtl numbers along the barrel axis.These two numbers are then used to calculate the Nusselt numbers from which the continuously changing convection heat transfer coefficients are determined.It is confirmed from an experimental firing process and its corresponding thermo-mechanical finite element analysis that the calculated coefficients present good estimate of the real coefficients.
gun barrel;heat convection;thermo-mechanical;thermo-chemistry
TJ391
A
1007-4414(2015)05-0050-03
10.16576/j.cnki.1007-4414.2015.05.016
2015-08-02
任华杰(1987-),男,辽宁沈阳人,硕士,助理工程师,主要从事火炮技术研究方面的工作。
