影像法测量齿轮径向跳动偏差不确定度及误差分析

2015-06-09许耀东

计量技术 2015年1期

关键词：蜗轮齿圈极差

许耀东郑卫

(上海工程技术大学，上海 200437)

影像法测量齿轮径向跳动偏差不确定度及误差分析

许耀东郑卫

(上海工程技术大学，上海 200437)

为解决齿轮离线单件测量中，需要额外配置心轴的工序，试验中对在无心轴的条件下，采用影像测量仪对齿轮测量进行了研究，并结合实例评定影像法测量的误差及不确定度，实现对不同规格齿轮径向跳动的测量目的。试验中通过误差来源分析，消除了存在的系统误差，并对测量结果进行了不确定度A类和B类综合评定，另外通过极差统计控制图法分析得到了近似的结果，两种途径对齿圈径向跳动精度等级判定结论一致，验证了误差分析的有效性。

影像测量；齿轮径向跳动；不确定度；误差修正；极差控制

0 引言

齿轮的齿圈径向跳动是指各齿间的固定弦到其旋转轴心线间距离的最大变动量，该值主要用来评定由齿轮几何偏心所引起的径向误差，齿圈径向跳动在齿轮传动中将引起齿轮传递运动的准确性[1]，它是评价齿轮传动精度的指标之一。目前对齿轮精度的测量理论主要有基于几何形状和位置精度的几何精度理论、基于齿轮传动质量和位置精度的传动精度理论、基于齿轮形状位置精度和传动精度的整体误差理论和基于统计学的统计精度理论[2]。按齿轮测量时序的不同，可分为离线测量、在机测量和在线测量。

齿圈径向跳动常用测量方法是直接法测量，可通过跳动检查仪、万能测齿仪和偏摆仪等，采用齿轮加装心轴并顶尖装夹的方法。选择合适的测头安置在齿槽中，一般测头直径为1.68倍的齿轮模数[3]。直接法测量时，齿轮需配置心轴，对心轴的制造精度、心轴与齿轮的安装精度及顶尖的同轴度都有很高的要求[4]。

伴随着光学影像技术和计算机软件技术的发展，一种基于机器视觉的影像法测量[5]，开始得到广泛应用。影像法测量在测量小模数齿轮及刚性差的齿轮方面发挥着很大的优势。实际上，机器视觉的影像法测量，属于静态条件下测量，而对于齿圈径向跳动来说，是反映齿轮旋转一周过程中所出现的误差。

为反映齿轮径向跳动的形态，试验中采用影像测量仪加回转工作台的办法进行测量。将齿轮放置于回转工作台上，事先调整齿轮中心、回转中心及投影仪十字线中心重合，然后移动十字线中心，使其落在齿轮分度圆的齿廓边缘上，按齿轮一定的分度角度旋转齿轮，观察十字线中心离开齿廓边缘的偏移量，实际上就是齿圈径向跳动偏差，取齿轮旋转一周，十字线中心离开齿廓的最大偏移与最小偏移之差即为齿圈径向跳动的数值。试验中采用影像测量仪加回转工作台的方法进行测量，减少了对心轴的依赖。可以在无心轴、顶尖装夹的条件下对多种规格齿轮进行单件测量。

1 齿轮径向跳动误差检测

图1 齿轮中心与回转工作台中心重合

试验中被测塑料齿轮模数m=3mm，齿数z=41。

图2 十字线中心落在齿廓边缘上

1.1 齿轮径向跳动公差说明

根据GB/T 10095.2—2001渐开线圆柱齿轮精度、径向综合偏差与径向跳动的定义和允许值，5级精度齿轮径向跳动公差通式为

(1)

d=50/125/180/…

mn=0.5/2/3.5/…

经计算被测齿轮分度圆直径d=mz=123mm

1.2 试验预处理

1.3 试验数据记录

齿轮转动2周，分别做2次试验，记录试验数据如表1和表2所示。

1.4 试验数据分析

将2次测量共16个数据，通过折线图进行分析，并添加趋势线，如图3所示。

61.862-61.500=0.362mm=362μm

式中，真值=理想分度圆半径值=mz/2=3×41/2=61.500mm。

表1 齿轮转动第1周测量数据

表2 齿轮转动第2周测量数据

图3 齿圈径向跳动分析图

这系统误差包括：人员测量的习惯性误差；蜗轮蜗杆传动返程间隙误差；齿轮转台十字线的同轴度误差。

根据图3分析，第1、2次试验测得齿轮径向跳动误差分别为520μm、1030μm。第1次的误差小于第2次的误差，通过线性趋势线分析，误差有增大的趋势。另外齿轮径向跳动误差呈现周期性的变化，如多项式趋势线所示。原因分析：由于蜗轮蜗杆传动中，存在返程间隙。每次旋转11圈即44°再反向旋转6′的角度，会造成手轮上读数变化而实际转台不动，这样随着测量次数的增加呈现测量误差有递增的趋势；另外由于在测量前需调整十字线中心和转台中心轴，以及十字线中心与齿轮中心轴重合对齐。而实际上转台、齿轮及十字线轴心不可能完全重合，存在一定的同轴度误差，由于偏心的存在，造成齿轮旋转过程中会出现近点和远点的差别，及在图中表现出周期变化的规律。

实际上十字线与转台的同轴度误差可控制在≤40μm。根据趋势线所示，蜗轮蜗杆返程间隙误差在1次试验中等于(62.1-61.6)/2=0.250mm=250μm。

通过测量该齿轮在1次测量中径向跳动误差为520μm，实际齿轮跳动误差应在520μm的基础上减去同轴度误差和蜗轮蜗杆返程间隙误差。通过误差调整，实际该齿轮在1次测量中径向跳动误差Fr=520-40-250=230μm,在2次测量中径向跳动误差Fr=1030-40-250=740μm。

2 测量误差

齿轮径向跳动测量过程存在齿轮安置偏心误差、蜗轮蜗杆回程间隙误差、蜗轮分度误差、仪器示值误差和重复测量误差[8]。其中齿轮安置偏心误差和蜗轮蜗杆回程间隙误差存在一定的变化规律，属于系统误差，可通过判断对结果进行修正。蜗轮分度误差、仪器示值误差和重复测量误差属于随机误差，可通过不确定度来进行评定。

2.1 系统误差

2.1.1 齿轮安置偏心误差δ1

试验中，十字线与转台的同轴度误差可控制在≤40μm，偏心误差δ1=40μm。

2.1.2 蜗轮蜗杆回程间隙误差δ2

根据趋势线所示，蜗轮蜗杆返程间隙误差在1次试验中

δ2=(62.1-61.6)/2=0.250mm=250μm。

结合上述两种误差，系统误差为40+250=290μm，误差修正值C=-290μm。

2.2 B类不确定度

2.2.1 蜗轮分度误差δ3

已知蜗轮分度误差有如下计算式

(2)

式中，Δφx为回转工作台的制造误差，此处取±30″(±0.000145rad)；rb为被测齿轮基圆半径；a 为被测齿轮分度圆压力角，取20°。

通过计算δ3=25μm。

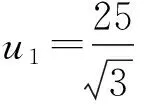
2.2.2 仪器示值误差δ4

试验中，选用的影像测量仪的分辨力为±5μm，所以测量仪器示值误差δ4=±5μm。根据数字式仪器在分度值内的示值误差服从均匀分布的原则[10]，示值误差产生的标准不确定度

2.3 A类不确定度

对齿轮径向跳动的重复测量会产生A类不确定度，可通过单值测量的实验标准差来衡定[11]。根据JJF 1059—1999《测量不确定度评定与表示》规定：在重复性条件下，对Xi进行n次独立观测，计算结果极差R，对于单次测量结果的实验标准差s(Xi)，当测量次数较小时可按下式近似评定[12]

s(Xi)=R/C=u(Xi)

(3)

式中系数C及自由度ν如表3所示。

根据表3数据，当测量次数N=8时，系数C=2.85，自由度ν=6.0。

表3 极差系数C及自由度v

可进行如下计算：

第1次独立测量的实验标准差为

(4)

第2次独立测量的实验标准差为

(5)

合成实验标准差为

(6)

已知R1=230，R2=740，C1=C2=2.85，ν1=ν2=6.0，代入上式，计算得s=191μm。

所以A类标准不确定度u3=s=191μm。

2.4 合成标准不确定度u

2.5 扩展不确定度U95

由于测量过程具有随机性，为表达测量结果，取大多数情况下包含因子k95=2，扩展不确定度U95=±k95·u=±2u=±384μm，置信概率p=95%。

3 极差统计控制

对于齿轮径向跳动的误差来说，是反映的最大值和最小值之差。根据2次独立测量的数据，如表4所示，这2组数据可以看作是总体中抽取的2个样本。而齿轮径向跳动实际上是样本的极差。应用统计过程控制方法[13]，对2组数据的极差分析如下。系统误差修正值C为-290μm。

表4 样本极差统计数据单位(mm)

应用极差R控制图的统计特性可得：

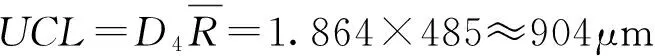
式中，D4、D3为查控制图统计表得到的系数。

经分析，A类和B类综合评定不确定度的测量结果485+384=869μm，比极差统计控制分析的UCL结果904μm偏小，而通过单值实验标准偏差±3s大小为903μm与极差控制图的UCL的结果904μm几乎一致。根据齿轮精度等级评定685<(869、904)<968，两种方法判定的齿轮径向跳动公差等级都为17级。然而值得注意的是，被测齿轮精度等级已经超出了根据GB/T 10095.2—2001所规定的齿轮径向跳动精度的13个等级，其中0级最高，12级为最低精度等级。究其原因是因为塑料齿轮在机械加工过程中，受到机械力和温度的影响，在齿廓上产生机械应力和热应力，进而导致齿廓产生应变，最终使齿廓出现非圆弧和飞边现象[7]，影响了齿廓精度。齿廓偏差过大最终导致齿轮径向跳动误差过大。

4 结论

影像法测量齿圈径向跳动，可实现在无心轴和顶尖装夹的条件下，对多规格的齿轮进行单件测量。测量前需调整齿轮中心、回转中心和投影十字线中心重合。由于回转偏心误差、回转分度误差、回程间隙误差及重复性测量误差的存在，使测量结果存在一定的系统误差和随机误差。为反映测量的不确定度，对系统误差进行修正，并运用A类和B类不确定度进行综合评定，另外通过极差控制图法对极差的控制极限也进行了评定。结果发现，两种方法对齿轮精度等级的判定结果一致，而极差统计控制图法计算误差极限相对更简单。由于被测机加工塑料齿轮齿廓加工中受到机械应力和热应力的作用，导致齿廓偏差过大，最终导致齿圈径向跳动过大。

[1] 王跃国,卢杏普.齿轮齿圈径向跳动测量结果的不确定度评定[J].计量技术,2009(6):68-69

[2] 谢华锟,冯刚,傅瑛,等.齿轮精度理论和测量技术的发展[J].工具技术,2009(11):3-7

[3] 张泰昌.齿轮检测500问[M].北京：中国标准出版社,2007

[4] 郭敬滨,张大厦,张继承,等.大齿轮测量中补偿安装偏心的研究[J].计量学报,2011(2):118-122

[5] 徐俊成,张莉彦,阎华,等.基于机器视觉的小模数塑料齿轮的在线检测[J].组合机床与自动化加工技术,2011(3):57-60

[6] 国家标准化管理委员会全国齿轮标准化技术委员会.GB/T 10095.2—2001渐开线圆柱齿轮精度第2部分:径向综合偏差与径向跳动的定义和允许值[S].北京：中国标准出版社,2002

[7] 许耀东,郑卫.软质齿轮影像法测量及系统误差和随机误差分析[J].光学技术,2010(5):744-748

[8] 陈刚,金雷鸣.齿轮跳动检查仪示值误差测量结果的不确定度评定[J].计量技术,2011(8):64-66

[9] 方仲彦,李岩.质量工程与计量技术基础[M].北京：清华大学出版社,2002

[10] 陈慧灵,钱征宇.试验筛影像测量新方法及其测量不确定度分析[J].计量技术,2011(6):35-37

[11] 常青.重复性测量在测量不确定度评定中的作用[J].中国计量,2006(10):82-83

[12] 国家质量技术监督局.JJF 1059—1999测量不确定度评定与表示[S].北京：中国计量出版社,1999