输电塔-线体系简化模型地震作用下的连续性倒塌分析①
2015-06-09王文明林清海曹丹京
徐 震, 王文明, 林清海, 金 树, 曹丹京, 田 利
(1.山东电力工程咨询院有限公司,山东 济南 250013; 2.山东大学土建与水利学院,山东 济南 250061)
输电塔-线体系简化模型地震作用下的连续性倒塌分析①
徐 震1, 王文明1, 林清海1, 金 树1, 曹丹京1, 田 利2
(1.山东电力工程咨询院有限公司,山东 济南 250013; 2.山东大学土建与水利学院,山东 济南 250061)
采用输电塔-线体系的简化模型,利用大型有限元软件ABAQUS对某输电塔进行地震作用下的连续性倒塌分析,研究输电塔的薄弱部位和倒塌全过程。分析结果表明,采用简化模型得到的输电塔薄弱环节和连续性倒塌过程与采用三塔四线模型得到的结果具有较好的一致性,简化模型可用于输电塔-线体系的连续性倒塌分析。
输电塔-线体系; 简化模型; 连续性倒塌分析; 地震作用
0 引言
高压输电线路是重要的生命线工程,在地震中一旦发生破坏,不但会造成重大的经济损失,还会给人们的生活带来严重影响。在历次大地震中,均有输电线路发生不同程度破坏的现象,输电塔倾斜或倒塌、断线、基础沉陷和绝缘子破坏是主要的破坏形式[1-4]。
近几十年,国内外很多学者研究了输电塔在地震作用下的响应。李宏男等[5]研究了大跨越输电塔的动力特性;岳茂光等[6]研究了输电塔-线体系在行波激励下的纵向地震响应;田利等[7]研究了输电塔-线体系在多点激励下的侧向地震响应;沈国辉等[8]研究了大跨越输电塔在地震作用下的响应。在以上的研究中,均未考虑材料的非线性。近十年来,国内外学者对输电塔进行了弹塑性分析。李宏男等[9]采用导(地)线简化为节点质量的方法,对不同类型输电塔的塑性极限状态进行了研究;王文明等[10]研究了材料的应变率效应对输电塔和导(地)线响应的影响;Albermani[11]建议对输电塔进行弹塑性分析,通过弹塑性分析可以对输电塔的设计进行修改和改进,从而提高输电塔的性能;王文明等[12]编制了ABAQUS软件的连续性倒塌分析子程序,对某输电塔-线体系进行了地震作用下的连续性倒塌分析,研究了输电塔在地震作用下的灾变过程。
输电塔-线体系在地震作用下的非线性时程分析较为复杂,为了简化计算,李宏男等根据大量的统计结果,提出了导(地)线简化为节点质量的方法。本文采用这种方法对某输电塔-线体系进行连续性倒塌分析,并与文献[12]的分析结果进行对比,研究这种简化模型在连续性倒塌分析时的可行性。
1 连续性倒塌分析子程序简介
结构的连续性倒塌是指由于外界作用(如地震、风和爆炸等)造成结构的局部破坏,并导致结构产生连续的破坏发展,使结构的大部分或全部发生坍塌。研究输电塔的连续性倒塌过程有助于确定输电塔的薄弱环节和破坏机理,可为改善结构体系或提高结构抗倒塌能力提供参考。结构连续性倒塌的数值模拟涉及几何非线性和材料非线性,单元间的接触和碰撞,以及结构的稳定性或机构运动等诸多问题。主要方法包括离散单元法、有限单元法、有限单元-离散单元组合方法和应用单元法[13-16],其中有限单元法是应用最为广泛的方法。
ABAQUS有限元分析软件具有强大的非线性分析功能,可用于各种大型复杂结构的分析。该软件提供了子程序接口,用户可以根据自己的需求编制子程序。文献[12]编制了可用于输电塔-线体系的连续性倒塌分析子程序。采用该子程序时,可根据材料的状态和失效准则对单元的状态进行时时控制。该子程序采用的本构关系如图1所示,在分析过程中,如果构件材料的应变达到极限应变,则认为该构件丧失承载能力。
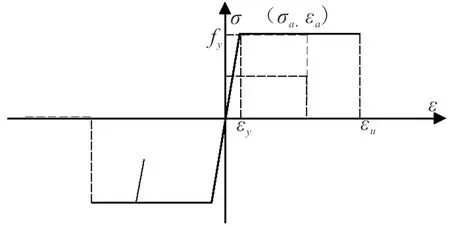
图1 钢材的应力-应变关系Fig.1 Stress-strain relationship of the steel
钢材单调加载应力-应变曲线关系为:
(1)
式中,ε和σ为应变和应力;Es为弹性模量;εy和fy为屈服应变和屈服强度;εu为极限应变,本文取为0.02。
钢材反复加载应力-应变关系为:
(2)
式中:σa为卸载点的应力;εa为卸载点的应变。
2 导(地)线简化方法
输电塔-线体系由输电塔、导(地)线和绝缘子组成。与输电塔的质量相比,导(地)线的质量较小,档距较大时导(地)线对输电塔的影响不可忽略。经过对输电塔-线体系大量的地震反应分析,李宏男等[8]提出了输电塔-线考虑导线影响的抗震计算简化模型(图2(图中仅显示包含横担的上部)),导(地)线简化为节点质量,将其添加到导(地)线与输电塔连接的部位。导(地)线附加质量的计算公式为:
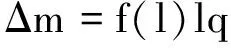
(3)
式中,l为导(地)线长度;q为导(地)线单位长度的质量;f(l)为附加质量系数,进行纵向抗震计算时的计算公式如式(4)所示,侧向抗震计算时的计算公式如式5所示。
(4)
(5)
式中,l0为界限档距,在纵向计算和侧向计算时的取值不同,并且与场地类别有关。对输电塔进行纵向计算时,l0取50m。对输电塔进行侧向计算时,软土场地取300m,中硬土场地取200m,硬土场地取150m。按照式(4)计算得到的数值如果超过0.7,取0.7。按照式(5)计算得到的数值如果超过1.0,取1.0。
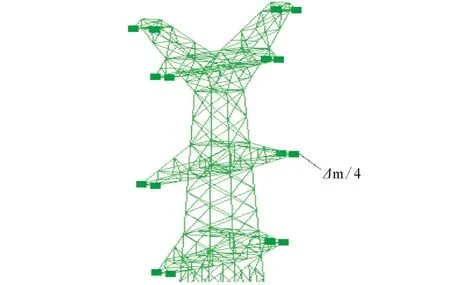
图2 塔-线体系简化模型Fig.2 Simplified model for tower-line system
3 分析模型
采用的输电塔模型如图3所示,塔体总高60.5 m,呼称高45 m,基础底宽为10.16 m,导线中点弧垂为10 m,塔-线体系的分析模型如图4所示。在ABAQUS软件中难以直接建立输电塔的模型,建模时首先在SAP2000中建立模型并找形,然后将未施加重力的模型导入ABAQUS软件中。
输电塔主材、斜材和辅材分别采用Q345和Q235的角钢,Q345钢和Q235钢的材料参数见表1。输电塔的每根构件划分为一个单元,单元类型为B31,输电塔杆件的截面信息参见文献[17]。导线采用LGJ-400/35型钢芯铝绞线,地线采用LGJ-95/55型钢芯铝绞线,绝缘子材料为陶瓷,导(地)线和绝缘子的截面及力学参数见表2。
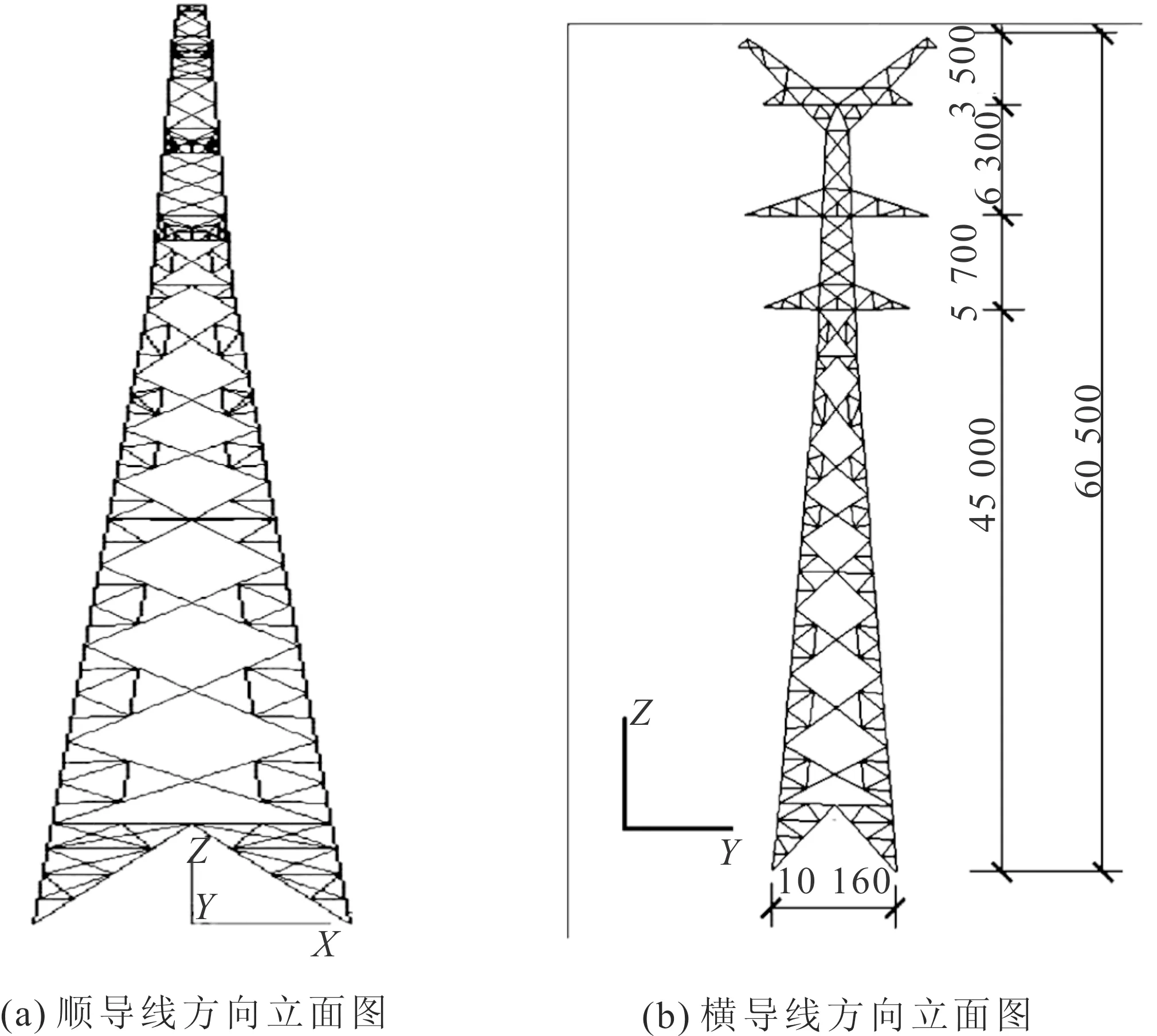
图3 输电塔立面图(单位:mm)Fig.3 Elevation of the transmission tower

图4 塔-线体系三维有限元模型Fig.4 Three-dimensional finite element model of the tower-line system
表1 Q345钢和Q235钢的力学参数
Table1 Mechanical parameters of steal Q345 and Q235

材料屈服强度/Pa弹性模量/Pa泊松比ρ/(kg·m-3)Q3453.45E+082.00E+110.37800Q2352.35E+082.00E+110.37800
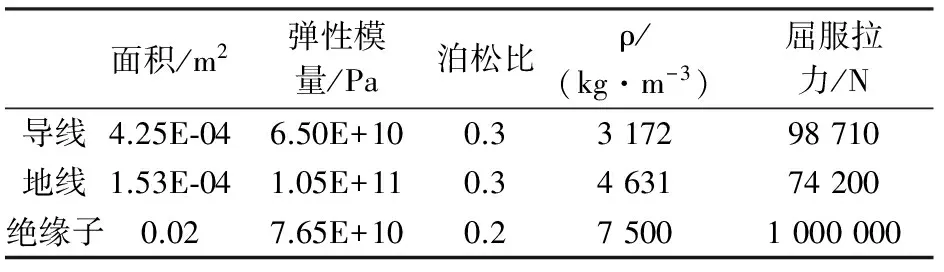
表2 导(地)线和绝缘子的力学参数
4 连续性倒塌分析
4.1 所采用的地震波
采用的地震波为Kobe波(1995)南北方向分量、Northridge波(1994)南北方向分量和El Centro波(1940)南北方向分量,峰值加速度分别调幅到20m/s2、40m/s2和25 m/s2,沿结构的横导线方向进行输入。
4.2 倒塌过程分析
采用简化模型对其进行地震作用下的连续性倒塌分析,在Kobe波作用下的连续性倒塌过程如图5所示(视图中不显示丧失承载能力的单元)。t=4.13 s时,Z=36.10 m和Z=47.97 m处的主材最先发生屈服;t=4.68 s时,Z=36.10 m和Z=34.90 m处的主材同时丧失承载能力;从t=6.00 s开始,输电塔大量的构件相继丧失承载能力;t=6.28 s时,输电塔丧失竖向传力路径。与文献[12]的分析结果进行对比,可以看出,采用简化模型时,构件发生屈服现象的时刻稍微提前,并位于相邻位置;出现构件丧失承载能力现象的时刻稍微提前,位置一致;输电塔发生连续性坍塌的范围较小;输电塔丧失竖向传力路径的时刻明显提前;Z=26.62 m处横隔的破坏较晚,与采用三塔四线模型分析结果明显不同。
简化模型在Northridge波作用下的连续性倒塌过程如图6所示。t=3.64 s时,Z=30.23 m处的主材最先屈服;t=3.65 s时,Z=36.10 m处的主材发生屈服;t=3.86 s时,Z=36.10 m和Z=34.90 m处的主材最先丧失承载能力;t=6.01 s时,输电塔丧失竖向传力路径。在整个倒塌过程中,Z=26.62 m处横隔及其以下部位的构件均未丧失承载能力。与文献[12]的分析结果进行对比,可以看出,采用简化模型时,构件发生屈服现象的时刻略微延后,处于相邻位置;构件出现丧失承载能力的时刻延后,但位置一致;输电塔丧失竖向传力路径的时刻明显提前;输电塔发生连续性坍塌的范围较小。

图5 简化模型在Kobe波作用下横导线方向的倒塌过程Fig.5 Collapse process of the simplified model alone the direction of transversal wire under Kobe wave
简化模型在El Centro波作用下的连续性倒塌过程如图7所示。t=2.31 s时,Z=41.97 m的主材发生屈服;t=2.35 s时,Z=36.10 m处的主材发生屈服;t=2.84 s时,Z=36.10 m处的主材丧失承载能力;t=5.10 s时,输电塔丧失竖向传力路径。与文献[12]的分析结果进行对比,采用简化模型时,构件发生屈服现象的时刻很接近,位置相邻;发生丧失承载能力现象的时刻明显提前,且不在同一位置;输电塔丧失竖向传力路径的时刻明显提前;输电塔发生连续性坍塌的范围较小。

图6 简化模型在Northridge波作用下顺导线方向的倒塌过程Fig.6 Collapse process of the simplified model along the direction of longitudinal wire under Northridge wave
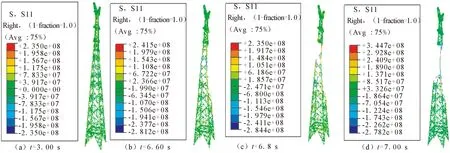
图7 简化模型在El Centro波作用下横导线方向的倒塌过程Fig.7 Collapse process of the simplified model along the direction of transversal wire under El Centro wave
由以上分析结果可以看出,采用导(地)线简化为节点质量的简化模型时,输电塔的薄弱部位位于Z=34.90 m附近,与采用塔-线体系模型的分析结果一致。采用两种分析模型得到的输电塔连续性倒塌过程也基本一致,不同之处在于横隔的破坏过程不同。采用三塔四线模型时,输电塔丧失竖向传力路径的时刻延后,发生连续性倒塌的范围较大。
5 结论
采用导(地)线简化为节点质量的方法,对某输电塔进行地震作用下的连续性倒塌分析,研究输电塔的薄弱部位和连续性倒塌全过程。通过与采用三塔四线模型的分析结果进行对比,可以看出,采用简化模型和三塔四线模型得到的结构薄弱部位和连续性倒塌过程基本一致,因此将导(地)线简化为节点质量的方法可用于地震作用下高压输电塔的连续性倒塌分析。
References)
[1] 李宏男,白海峰.高压输电塔-线体系抗灾研究的现状与发展趋势[J].土木工程学报,2007,40(2):39-46.LI Hong-nan,BAI Hai-feng.State-of-the-art Review on Staties of Disaster Resistance of High-voltage Transmission Tower-line Systems[J].China Civil Engineering Journal,2007,40(2):39-46.(in Chinese)
[2] 童林旭.城市生命线系统的防灾减灾问题:日本阪神大地震生命线震害的启示[J].城市发展研究,2000(3):8-12.TONG Lin-xu.Disaster Prevention and Relief of the Urban Lifeline System[J].Urban Studies,2000(3):8-12.(in Chinese)
[3] 谢强,李杰.电力系统自然灾害的现状与对策[J].自然灾害学报,2006,15(4):126-131.XIE Qiang,LI Jie.Current Situation of Natural Disaster in Electric Power System and Counter Measures[J].Journal of Natural Disasters,15(4):126-131.(in Chinese)
[4] 张子引,赵彪,曹伟炜,等.四川汶川8.0级地震电网受灾情况调研与初步分析[J].电力技术经济,2008,20(4):1-4.ZHANG Zi-yin,ZHAO Biao,CAO Wei-wei,et al.Investigation and Preliminary Analysis of Damages on the Power Grid in the Wenchuan Earthquake ofM8.0[J].Electric Power Technologic Economics,2008,20(4):1-4.(in Chinese)
[5] 李宏男,王前信.大跨越输电塔体系的动力特性[J].土木工程学报,1997,30(5):28-36.LI Hong-nan,WANG Qian-xin.Dynamic Characteristics of Long-span Transmission Lines and Their Supporting Towers[J].China Civil Engineering Journal,1997,30(5):28-36.(in Chinese)
[6] 岳茂光,李宏男,王东升,等.行波激励下输电塔-导线体系纵向地震反应分析[J].中国电机工程学报,2006,26(23):145-150.YUE Mao-guang,LI Hong-nan,WANG Dong-sheng,et al.Longitudinal Response of the Power Transmission Tower-cable System Under Traveling Seismic Wave Excitations[J].Proceedings of the CSEE,2006,26(23):145-150.(in Chinese)
[7] 田利,李宏男,黄连壮.多点激励下输电塔-线体系的侧向地震反应分析[J].中国电机工程学报,2008,28(6):108-114.TIAN Li,LI Hong-nan,WANG Dong-sheng,et al.Lateral Response of Transmission Tower-line System Under Multiple support Excitations[J].Proceedings of the CSEE,2008,28(6):108-114.(in Chinese)
[8] 沈国辉,孙炳楠,何运祥,等.大跨越输电塔线体系的地震响应研究[J].工程力学,2008,25(11):212-217.SHEN Guo-hui,SUN Bing-nan,HE Yun-xiang,et al.Seismic Response of Long-span Transmission Tower-line System[J].Engineering Mechanics,2008,25(11):212-217.(in Chinese)
[9] 李宏男,胡大柱,黄连状.地震作用下输电塔体系塑性极限状态分析[J].中国电机工程学报,2006,26(24):192-199.LI Hong-nan,HU Da-zhu,HUANG Lian-zhuang.Plastic Limit Analysis of the Transmission Tower System Subjected to Earthquake Action[J].Proceedings of the CSEE,2006,26(24):192-199.(in Chinese)
[10] Wenming Wang,Hongnan Li,Guohuan Liu.Strain Rate Effect on Transmission Tower-line System Under Earthquake Action[J].Advanced Materials Research,2011,243-249:5845-5848.
[11] Albermani F,Kitipornchai S,Chan R W K.Failure Analysis of Transmission Towers[J].Engineering Failure Analysis,2009,16(6):1922-1928.
[12] Wenming Wang,Hongnan Li,Tian Li.Progressive Collapse Analysis of Transmission Tower-line System Under Earthquake[J].Advanced Steel Construction,2013,9(2):161-172.
[13] Cundall P A,Strack O D L.A Distinct Numerical Model for Granular Assemblies[J].Geotechnique,1979,29(1):47-65.
[14] Lu X Zh,Lin X Ch,Ye L P,et al.Daiyuan Tang.Numerical Models for Earthquake Induced Progressive Collapse of High-rise Buildings[J].Engineering Mechanics,2010,27(11):64-70.
[15] Munjiza A,Bangash T,John N W M,The Combined Finite-Discrete Element Method for Structural Failure and Collapse[J].Engineering Fracture Mechanics,2004,71(4/6):469-483.
[16] Meguro K,Tagel-Din H.Applied Element Method for Structural Analysis:Theory and Application for Linear Materials[J].Struct Engrg/Earthquake Engrg,2000,17(1):21-35.
[17] 王文明.考虑应变率效应的结构抗震分析方法研究[D].大连:大连理工大学,2013.WANG Wen-ming.Study on the Seismic Analysis Method of Structure Considering Strain Rate Effect[D].Dalian: Dalian University of Technology,2013.(in Chinese)
Progressive Collapse Analysis of a Simplified Model for Transmission Tower-line Coupled System under Seismic Action
XU Zhen1, WANG Wen-ming1, LIN Qing-hai1, JIN Shu1, CAO Dan-jing1, TIAN Li2
(1.ShandongElectricPowerEngineeringConsultingInstituteCorporationLimited,Jinan,Shandong250013,China;2.SchoolofCivilandHydraulicEngineering,ShandongUniversity,Jinan,Shandong250061,China)
Overhead high-voltage electric-transmission lines play an important role in the operation of a reliable electrical power system.Damage to these lines can cause great economic loss and bring inconvenience to human life.A substantial number of transmission lines have been damaged by catastrophic earthquakes around the world.The transmission tower tilt or collapse,conductor breakage,foundation subsidence,and insulator destruction were the major types of failure.It is necessary to study not only the seismic response of transmission lines in the elastic and plastic phases but also their collapse process.Progressive collapse analysis is a well-understood physical occurrence in which the loss of local load-bearing capacity propagates through a system,precipitating complete collapse or a major portion of it.The vulnerable points,collapse mode,and capacity of the structure can be evaluated by it,and these data can be used for the design of new towers or for evaluating existing towers.Many scholars have studied the nonlinear responses of single transmission towers or tower-line coupled systems.Numerical simulation of progressive collapse is a challenging task,which includes material and geometric nonlinearity,contact and collision between elements,and losing the load-bearing capacity of elements.Nowadays,there are mainly four numerical analytical methods used for the collapse analysis:the discrete-element method (DEM),combined finite-discrete element method,applied-element method (AEM),and finite-element method (FEM).The FEM,based on continuum mechanics,is the most widely used method in structural engineering.For linear elastic problems,the method has proved to be advantageous.Furthermore,the method is very effective for solving nonlinear problems by using reasonable constitutive relationships.The method can be used in the solution of large-scale and complex industrial problems,while other methods are extremely difficult to use.During the collapse process under an earthquake,some elements lose load-bearing capacity,which is a problem for the FEM.Commonly,the method of removing these elements is used,which is called the birth-death element method.The conductors and ground wires can be simplified as concentrated masses for the seismic analysis of transmission tower-line coupled systems.In this paper,this method is used.With the simplified model,by using the finite-element program ABAQUS,the progressive collapse analysis of a transmission tower under an earthquake is conducted.The results show that the vulnerable points and progressive collapse process obtained are in good accord with the results obtained by using the tower-line coupled system with three towers and four span lines.Therefore,the simplified model can be used in the seismic analysis of transmission tower-line coupled systems.
transmission tower-line coupled system; simplified model; progressive collapse analysis; earthquake action
2014-07-01
国家自然科学基金项目(51208285);中国博士后科学基金项目(2012M521338)
徐 震(1981-),男,工程师,主要从事输电线路设计与研究工作.
田 利(1982-),男,博士(后),副教授,主要从事结构抗震研究.E-mail:tianli@sdu.edu.cn
TU312.3
A
1000-0844(2015)02-0304-06
10.3969/j.issn.1000-0844.2015.02.0304
