基于应力波法的锚杆（索）锚固质量动力检测数值模拟研究

邓东平，李 亮，赵炼恒

（中南大学土木工程学院，长沙 410075）

基于应力波法的锚杆（索）锚固质量动力检测数值模拟研究

邓东平，李 亮，赵炼恒

（中南大学土木工程学院，长沙 410075）

锚杆（索）大量应用于边坡工程加固，为保证锚杆（索）发挥作用，一般采用应力波法对其锚固质量进行检测，检测的2个主要指标是：锚杆（索）长度和缺陷段的位置。为此，在ANSYS/LS-DYNA中建立锚固体应力波动力分析模型，将小锤对锚杆（索）的敲击作用等效为小锤按一定激发速度v0与锚杆（索）的碰撞，并在锚杆（索）端头断面中点采集应力波信号。经算例与理论研究成果对比，验证了数值模型的可行性，同时，分析了小锤弹性模量和激发速度v0的取值对应力波信号的影响，研究了应力波法判别缺陷段位置的准确性，及对比了端头激发与端头和底端同时激发这2种方式在锚杆（索）质量检测中的适用性。研究结果表明：①小锤弹性模量的增大仅对初始应力波信号有增强作用，对经锚固体底端一次反射回的应力波信号影响不大，而小锤激发速度v0的增大对初始和经锚固体底端一次反射回的应力波信号均有利，且与后者成线性比例关系；②应力波法对锚固体缺陷段位置的判别较为可靠，且缺陷段越饱满判别准确性越高；③端头和底端同时激发方式缩短了反应锚固体断面变化处和底端位置的应力波信号时间，因而有利于工程应用。

锚杆（索）；应力波；数值模拟；锚固质量；缺陷段；饱满度；激发方式

2015，32（01）：62－69

1 研究背景

锚杆（索）作为一种可靠的加固方式，广泛应用于边坡工程处置［1－3］。然而，为了保证锚杆（索）施加的压力能够对滑动岩土体起到有效抑制作用，一方面需锚杆（索）达到设计长度，另一方面锚杆（索）必须保证锚固质量（即灌浆不存在缺陷段和预应力出现松弛），使其在寿命期内能有效工作。目前，检测锚杆（索）锚固质量的方法主要有2种：传统载荷试验法和无损检测方法［4－8］。无损检测法是通过在锚杆（索）端头激发应力波，然后，在锚杆（索）端头采集应力波信号来判别各断面变化处的信息，以此获得锚杆（索）的长度（包括自由段和锚固段长度）及锚固体缺陷段的位置。

在锚杆（索）锚固质量应力波法检测中，大多数采用实验法和数值模拟分析法，如李义等［9］通过室内试验验证了应力反射波法检测锚杆的锚固质量的可行性，刘海峰等［10］采用试验方法研究了应力波在锚固介质中的传播波速与锚固质量的定性关系，张世平等［11］基于实验探索了利用高频段多频率导波检测锚固锚杆长度的方法，张昌锁等［12］、张东方［13］、吕丹丹［14］和梁龙龙［15］等验证了采用数值模拟方法研究锚杆（索）锚固质量的可行性，并分析了相关参数取值对应力波信号的影响。然而，采用应力波法对锚杆（索）锚固质量进行检测的研究还存在一些不足需要完善，如激发应力波振源小锤的参数选取、缺陷段位置识别程度的正确性和应力波激发方式适用性分析等。

本文在ANSYS/LS-DYNA中建立锚固体质量动力分析模型。首先，比较数值模拟与理论计算结果，验证模型的可行性；然后，选取不同的小锤弹性模量和激发速度，分析其对应力波信号的影响；针对存在缺陷段锚固体，研究采用应力波法判别缺陷段位置的准确性，将端头激发与端头和底端同时激发这2种激发方式进行对比，以此探讨其对不同锚固体质量检测的可行性与适用性。

2 锚杆（索）锚固质量检测的应力波法原理

2.1 纵向应力波传播的波动方程

一般情况下，由锚杆（索）和外围注浆体组成的锚固体可等效为一个直的等截面细长杆，如图1所示，设x表示锚固体中某一横截面坐标，u（x，t）为该截面的纵向位移，σ（x，t）为该截面承受的动应力，q（x，t）为单位体积上的体积力，取锚固体中微小单元进行受力分析，可得到该微单元在x方向上的运动平衡方程，即

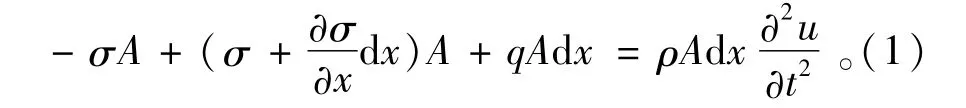
式中：A为锚固体面积；ρ为锚固体密度。

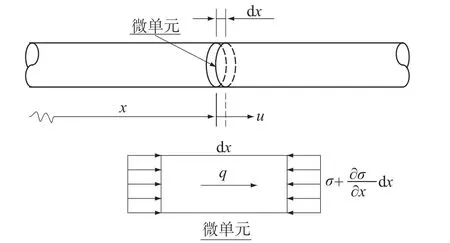
图1 锚杆（索）微单元应力模型Fig.1 M icro-element stressmodel of rock bolt（cable）

当忽略体积力q时，由式（1）可得应力波在杆中传播的一维波动方程［16］，即

式中：E为锚固体弹性模量；c0为应力波在锚固体中的传播速度，。

2.2 应力波在锚固体断面变化处的反射与透射

应力波在传播过程中，当锚固体断面尺寸发生变化（如自由段转锚固段或锚固段中存在缺陷）时，应力波会在断面变化处界面上发生反射和透射。

如图2所示，设入射应力波为I，反射应力波为R，透射应力波为T，断面变化处MN左侧锚固体的材料参数为：面积A1、弹性模量E1、密度ρ1、应力波传播波速c01。断面变化处MN右侧锚固体的材料参数为：面积A2、弹性模量E2、密度ρ2、应力波传播波速c02。

图2 应力波在锚固体断面变化处反射和透射计算模型Fig.2 Calculation model of reflection and transm ission of stresswave on changed section of anchorage body

根据应力波在锚固体断面变化处的位移、速度和力的连续条件及一维应力波的波动方程，可得反射波、透射波与入射波的应力和速度关系式如下：

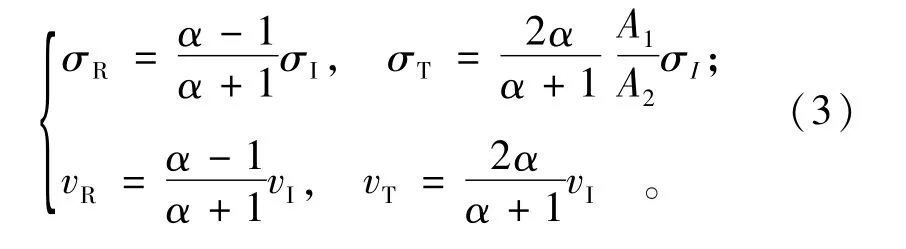
式中：σI，σR和σT分别为入射波、反射波和透射波的应力；vI，vR和vT分别为入射波、反射波和透射波的速度；α为阻抗，α＝（E2A2/c02）/（E1A1/c01），c01和c02分别为应力波在锚固体1和锚固体2中传播的速度，。

当断面变化处MN右侧为自由边界时（即σT＝0），则阻抗α＝0；当断面变化处MN右侧为固定边界时（即vT＝0），则阻抗α＝∞。

由此，可根据波动方程式（2）和锚固体断面变化处关系式（3），及应力波初始条件和边界条件，即可得到应力波整个传播过程中各断面的应力、速度和位移值。

2.3 锚杆（索）锚固质量检测指标

考察锚杆（索）锚固质量，一般采取2个指标判别：①锚杆（索）长度；②缺陷段存在的位置。这二者均可通过在锚杆（索）端头中点收集应力波信号，以此判别从端头到锚固体断面变化处和底端位置所需的时间，然后再根据已知的应力波传播速度，即可得知锚杆（索）长度及锚固体断面变化处的位置。

3 锚固体中应力波传播动力分析的ANSYS/LS-DYNA模型建立

如图3（a）所示，将实际中的锚杆（索）的横断面等效成半径为r的圆，外围注浆体等效成外径为R、内径为r的圆环，锚固体在ANSYS/LS-DYNA中建立的数值模型和网格划分如图3（b）所示。由于在锚杆（索）端头激发应力波所产生的作用较小，故不会导致锚杆（索）和外围注浆体的接触面产生相对位移，因此，在数值模型中，将锚杆（索）外表面和外围注浆体内表面的节点粘合在一起。

图3 锚固体动力检测分析模型Fig.3 Dynam ic testingmodel of anchorage body

实际应力波的激发是让小锤对锚杆（索）进行敲击，在数值模拟中将此过程简化为小锤按一定速度v0碰撞锚杆（索），如图3（c）所示，其中，速度v0的大小可表示敲击力的大小，小锤与锚杆（索）的横断面大小一致。

锚杆（索）、外围注浆体和小锤在数值模拟中所选用的材料参数如表1。

表1 实体材料参数取值Table 1 M aterial parameters

由于锚杆（索）弹性模量Es一般为定值，此时，小锤弹性模量E的取值对由其激发的应力波信号有一定影响，故将该取值作为后续算例分析的一个因素。

当小锤激发应力波后，在锚杆（索）端头断面中心点采集应力波信号，然后，根据该点收集到的初始、各断面变化处和锚固体底端反射回的应力波信号，以此判别应力波在锚固体中的传播波速（当锚杆（索）长度确定时）、锚杆（索）长度和锚固体断面变化处位置（当应力波传播波速确定时），以及应力波信号强弱（采用应力波振动速度幅值大小表示）。

4 计算对比分析

4.1 算例对比

按照第3节建立的锚固体动力分析模型，其中，为了便于与理论研究成果进行对比，将小锤按一定速度v0敲击锚杆（索）的作用简化为如图4所示的荷载曲线。模拟取锚杆（索）的长度L分别为10，15，20 m，考虑锚固体底端约束分别为固定和自由这2种工况，锚杆（索）和外围注浆体的材料参数取值见表1。

图4 载荷曲线Fig.4 Load curve

为了便于分析，现将在锚杆（索）端头断面中点采集的应力波信号说明如图5所示，其中，t1为初始应力波振动速度幅值v1对应时刻，t2为经锚固体底端一次反射回的应力波振动速度幅值v2对应时刻，由此根据已知的锚杆（索）长度L，即可得应力波的传播波速，且所得数值模拟计算结果如表2。

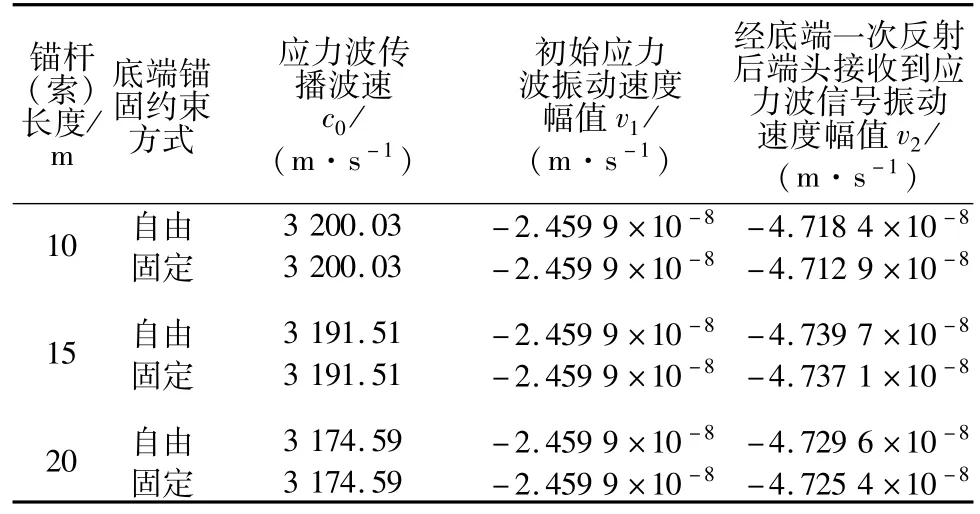
表2 数值模拟结果Table 2 Results of numerical simulation

同时，当锚杆（索）长度分别为10，15，20 m及锚固体底端分别为自由和固定约束时，采用文献［17］复合锚固体计算方法，得到应力波在锚杆（索）中传播的波速c0均为3 184.88 m/s；采用应力波特征线法理论分析，得到初始应力波振动速度幅值v1均为－2.386 8×10－8m/s和经底端一次反射后端头接收到应力波信号振动速度幅值 v2均为－4.773 6×10－8m/s。对比可知，理论研究成果与数值模拟结果基本一致，说明建立的数值模型对锚固体进行动力分析是可行的。

4.2 小锤弹性模量和激发速度取值对应力波信号的影响

小锤参数的选取必然对由其激发的应力波信号存在一定的影响。通常情况下，小锤的弹性模量（即软硬程度）E和激发速度v0是2个最为主要的影响因素。在本例中取锚杆（索）长度L＝15 m，锚杆（索）、外围注浆体和小锤的材料参数如表1，锚固体底端分别为自由和固定约束方式。当小锤的弹性模量E分别为0.5×1010，4.4×1010，8.3×1010，12.2×1010，16.1×1010，20.0×1010Pa，激发速度v0分别为1，0.8，0.6，0.4，0.2 m/s时，研究小锤弹性模量E和激发速度v0不同对应力波信号的影响。

其中，当小锤的激发速度v0＝1 m/s，弹性模量E分别为0.5×1010，20×1010Pa时，锚杆（索）端头断面中点采集到的应力波振动速度与时间的关系如图6（a）和图6（b），当小锤的激发速度v0＝0.2 m/s，弹性模量E分别为0.5×1010，20×1010Pa时，锚杆（索）端头断面中点采集到的应力波振动速度与时间的关系如图6（c）和图6（d）。

图6 在锚固体底端不同约束情况下的锚杆（索）端头断面中点应力波振动速度信号Fig.6 Vibration velocity signal of stress wave on m idpoint of the section of rock bolt（cable）top when the bottom of anchorge body is confined freely or fixed ly

由图6可知：当锚固体底端为自由约束方式时，初始与经锚固体底端一次反射回的应力波振动速度信号相位相同，而当锚固体底端为固定约束方式时，初始与经锚固体底端一次反射回的应力波振动速度信号相位反向，故与应力波传播理论结论一致，同样说明本文数值模型的正确性。

不同小锤弹性模量E和激发速度v0下，得到的应力波在锚固体中传播的波速c0如图7，初始与经底端一次反射回的应力波振动速度的相对比值（即不同小锤弹性模量E和激发速度v0时的应力波振动速度幅值与E＝0.5×1010Pa和v0＝0.2m/s时的该值之比）如图8。

图7 应力波传播波速对比Fig.7 Com parison of propagation velocity of stress wave

图8 应力波振动速度幅度相对比值Fig.8 Relative ratio of vibration velocity am p litudes of stress waves

由图7、图8可知：①小锤弹性模量E及激发速度v0的变化对应力波在锚固体中传播的波速影响不大，与前述应力波波速c0计算公式表述一致，其仅与被测物体的弹性模量和密度有关；②随着小锤弹性模量E及激发速度v0的增大，初始应力波的振动速度幅值总趋势是增大的，但变化无规律性；③经锚固体底端一次反射回的应力波的振动速度幅值与小锤激发速度v0基本成线性增大关系，但小锤弹性模量E的增大对其幅值影响不明显。

4.3 存在缺陷段锚固体动力分析

在实际锚杆（索）质量检测中，除了采用应力波法分析得到锚杆（索）的长度外，另一个主要的检测指标是缺陷段位置的判别。

如图9所示，以锚杆（索）端头断面中点为原点O，锚杆（索）长度方向为x轴，取锚杆（索）长度L＝15 m，锚固段1的长度L1＝8 m，缺陷段的长度L2，锚固段2的长度L3，锚杆（索）、外围注浆体和小锤的材料参数如表1，锚固体底端为自由约束方式，其中，小锤的弹性模量E＝0.5×1010Pa，激发速度v0＝1 m/s。当设缺陷段实际长度L2分别为0.5，1，1.5，2，2.5，3，3.5，4 m及缺陷段外围注浆体饱和度n分别为0%，30%，60%，90%时，研究采用应力波法分析得缺陷段位置与实际位置相差百分比，即缺陷段起始与终止断面位置判别值（即图9中断面1和断面2到端头的距离）和实际位置值的差值与实际位置值之比的百分数）如图10所示。

图9 存在缺陷段锚固体模型Fig.9 M odel of anchorage body w ith defective segment

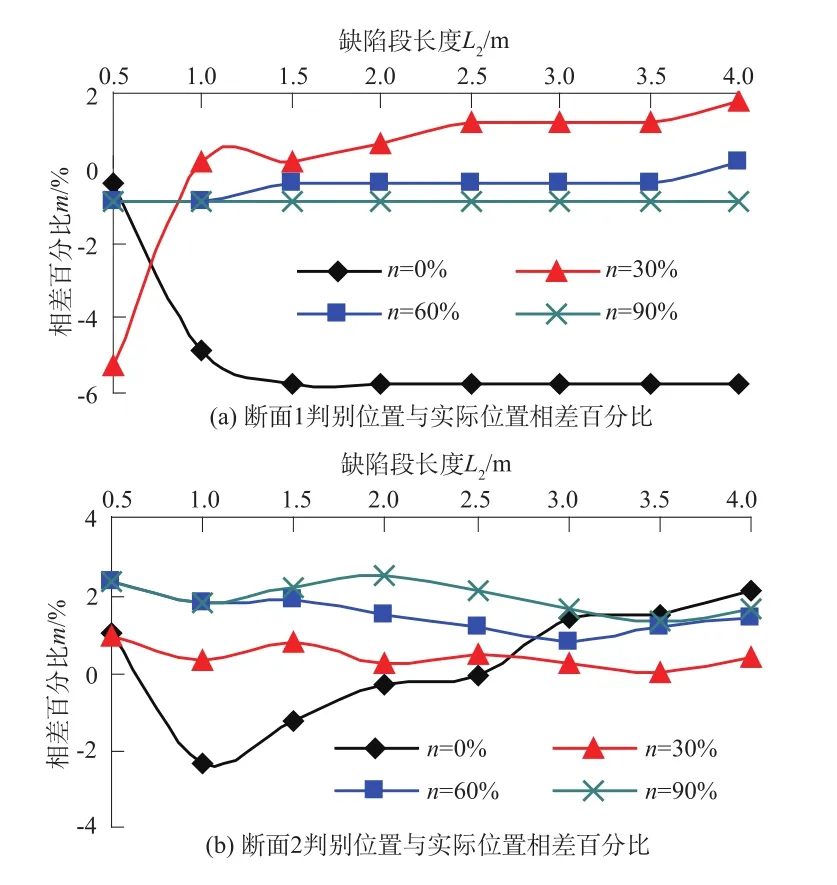
图10 缺陷段判别位置与实际位置相差百分比Fig.10 Percentage of the deviation between detected and actual position of defective segment

由图10可知：①采用应力波法判别得的缺陷段位置与其实际位置相差基本不大，说明采用应力波法来分析锚杆（索）的质量是可行的；②缺陷段外围注浆体的饱满程度越高，判别得的缺陷段位置与实际位置越接近。其原因在于锚杆（索）质量动力分析时，应力波在锚固体中的传播波速c0是以锚杆（索）全长与应力波从端头传播到底端所需时间的比值来计算的，然而，当存在缺陷段时，应力波在锚固段中的传播波速与在缺陷段中的传播波速不一致，这样使分析得的缺陷段位置与实际位置存在差别，尤其是缺陷段饱满度越低时，应力波在锚固段和缺陷段中的传播波速差别越大，因而，造成的误差也越大。

4.4 不同激发方式下锚固体动力分析

一般情况下，应力波采用端头激发方式，这种激发方式的一个特点是要获得锚固体断面变化处及底端的位置需经此界面反射回应力波信号，即判别锚固体断面变化处及底端位置需应力波来回往复一次，因此，采用此激发方式在端头接收到的应力波信号的时间较长。为此，在本例中采用端头和底端同时激发方式以缩短判别锚固体断面变化处及底端位置所需应力波的传播时间。

如图11所示，选取2种常见的锚固体型式：①存在自由段非全长注浆型锚固体，锚杆（索）长度L＝15 m，自由段长度L1＝10 m，锚固段长度L2＝5 m；②存在缺陷段全长注浆型锚固体，锚杆（索）长度L＝15 m，锚固段1长度L1＝8 m，缺陷段长度L2＝2 m，锚固段2长度L3＝5 m，且缺陷段外围注浆体的饱和度n分别为0%，50%，100%。锚杆（索）、外围注浆体和小锤的材料参数如表1，其中，小锤的弹性模量E＝0.5×1010Pa，激发速度v＝1 m/s，锚固体底端约束为自由约束方式，这2种激发方式下锚杆（索）端头断面中点采集到的应力波振动速度信号如图12、图13所示。

图11 不同锚固体型式下2种应力波激发方式模型Fig.11 M odel of two excitation modes in the presence of different types of anchorage body

由图12、图13可知：端头和底端同时激发方式与端头激发方式一样均能较清晰地判别锚固体断面变化处（即锚杆（索）自由段与锚固体交界面、锚固体缺陷段起始和终止断面）的位置及锚杆（索）的长度。同时，端头和底端同时激发方式获得反应断面变化处和底端信息的应力波信号所需时间均小于或等于端头激发方式。因此，端头和底端同时激发方式较端头激发方式更适合于实际工程中存在应力波衰减时的锚杆（索）质量分析。

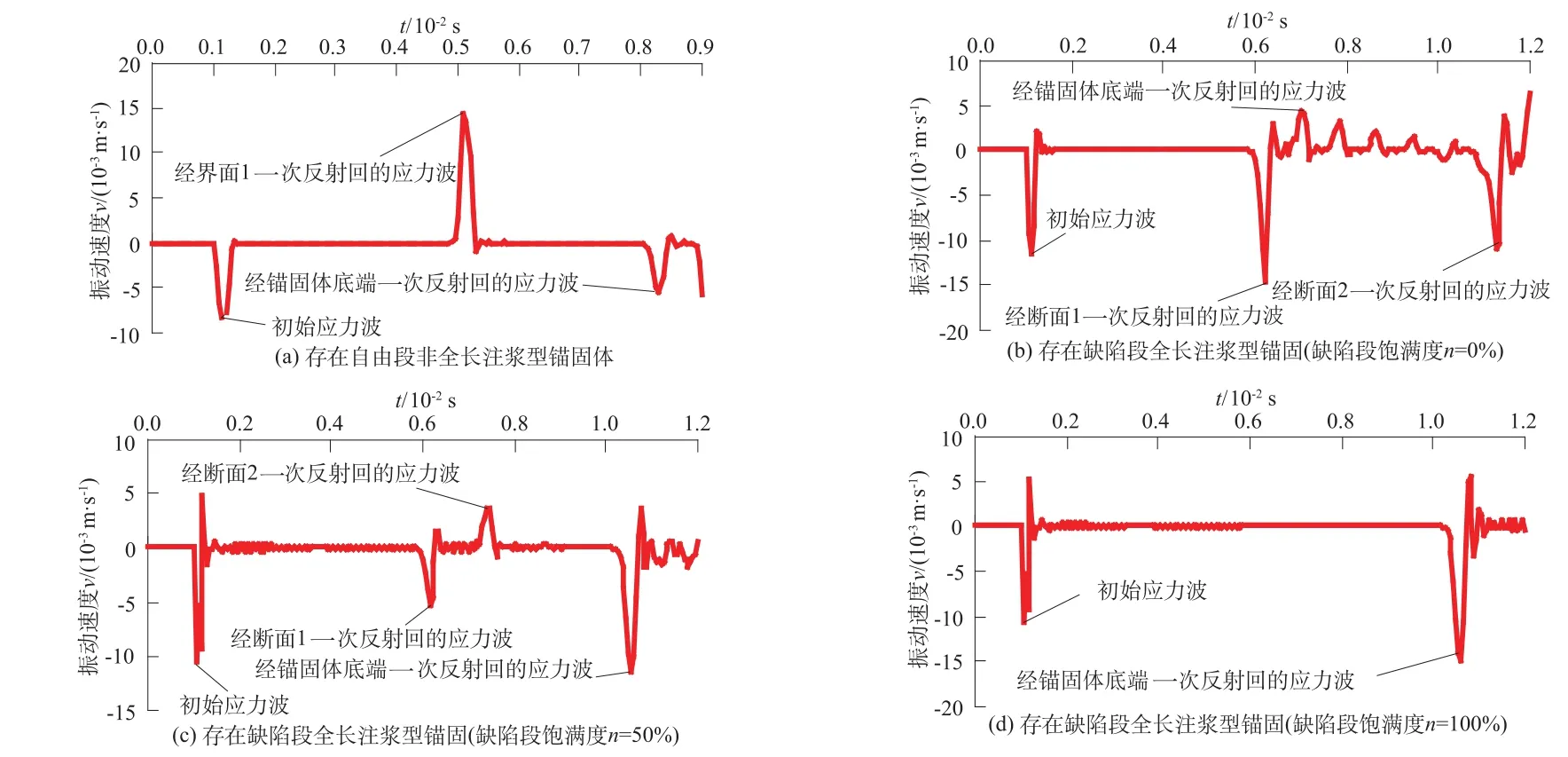
图12 端头激发方式下锚杆（索）端头断面中点的应力波振动速度信号Fig.12 Vibration velocity signal of stresswave on m idpoint of the section of rock bolt（cable）top in the presence of excitation on top

图13 端头和底端同时激发方式下锚杆（索）端头断面中点的应力波振动速度信号Fig.13 Vibration velocity signal of stresswave on m idpoint of the section of rock bolt（cable）top in the presence of excitation on top and bottom simultaneously

5 结 论

（1）经与理论研究成果对比分析可知，采用数值模拟方法分析锚杆（索）锚固质量应力波动力检测是可行的。

（2）采用小锤敲击锚杆（索）激发应力波时，随着小锤弹性模量和激发速度的增大，端头初始应力波信号同样增大，经锚固体底端一次反射回的应力波信号与激发速度成线性增大关系，但受小锤弹性模量的影响较小。

（3）对于存在缺陷段锚固体，缺陷段饱满程度越高分析得到的缺陷段位置越准确。

（4）端头和底端同时激发方式较端头激发方式明显减少了判别反应锚固体断面变化处和底端位置的应力波信号时间，因而，该激发方式更利于工程应用。

［1］付宏渊，蒋中明，李怀玉，等.锚固岩体力学特性试验研究［J］.中南大学学报（自然科学版），2011，42（7）：2095－2101.（FU Hong-yuan，JIANG Zhong-ming，LI Huai-yu，et al.Mechanics Properties of Anchored Rock［J］.Journal of Central South University（Science and Technology），2011，42（7）：2095－2101.（in Chinese））

［2］谌文武，张宇翔，和法国，等.基于FLAC和遗传算法的斜坡加固方案优化方法［J］.中南大学学报（自然科学版），2011，42（11）：3507－3514.（CHENWen-wu，ZHANG Yu-xiang，HE Fa-guo，etal.Optimization Methodfor Slope Reinforcement Design Based on FLAC and Genetic Algorithms［J］.Journal of Central South University（Science and Technology），2011，42（11）：3507－3514.（in Chinese））

［3］韩 斌，郑禄†n，王少勇，等.复杂破碎露天边坡的综合加固技术［J］.中南大学学报（自然科学版），2013，44（2）：772－777.（HAN Bin，ZHENG Lu-jing，WANG Shao-yong，et al.Synthetic Reinforcement of Complicated and Broken Open Pit Slope［J］.Journal of Central South University（Science and Technology），2013，44（2）：772－777.（in Chinese））

［4］BEARDM D，LOWEM JS，CAWLEY P.Developmentof a Guided Wave Inspection Technique for Rock Bolts［J］.Insight，2002，44（1）：19－24.

［5］BEARD M D，LOWE M J S.Non-destructive Testing of Using Guided Ultrasonic Waves［J］.International Journal of Rock Mechanics and Mining Sciences，2003，40（4）：527－536.

［6］IVANOVIC A，RICHARD D N，ALBERT A R.Influence of Pre-stress on the Dynamic Response of Ground Anchorages［J］.Journal of Geotechnical and Geoenvironmental Engineering，2002，（3）：237－249.

［7］PAVLAKOVIC B N，LOWE JS，CAWLEY P.High Frequency Low-loss Ultrasonic Modes in Imbedded Bars［J］.Journal of Applied Mechanics，2001，68（2）：67－75.

［8］MADENGA V，ZOU D H，ZHANG C.Effects of Curing Time and Frequency on Ultrasonic Wave Velocity in Grouted Rock Bolts［J］.Journal of Applied Geophysics，2006，59（1）：79－87.

［9］李 义，王 成.应力反射波法检测锚杆锚固质量的实验研究［J］.煤炭学报，2000，25（2）：160－164.（LI Yi，WANG Cheng.Experimental Study on Bolt Bonding Integrity with Stress Reflected Wave Method［J］.Journal of China Coal Society，2000，25（2）：160－164.（in Chinese））

［10］刘海峰，杨维武，李 义.全长锚固锚杆早期锚固质量无损检测技术［J］.煤炭学报，2007，32（10）：1066－1069.（LIU Hai-feng，YANG Wei-wu，LI Yi.Non-destructive Testing Technology of All Lengthy Anchorage Rock Bolt at Early Age［J］.Journal of China Coal Society，2007，32（10）：1066－1069.（in Chinese））

［11］张世平，张昌锁，白云龙，等.注浆锚杆完整性检测方法研究［J］.岩土力学，2011，32（11）：3368－3372.（ZHANG Shi-ping，ZHANG Chang-suo，BAIYun-long，et al.Research on Method for Detecting Integrity of Grouted Rock Bolts［J］.Rock and Soil Mechanics，2011，32（11）：3368－3372.（in Chinese））

［12］张昌锁，李 义，赵阳升，等.锚杆锚固质量无损检测中的激发波研究［J］.岩石力学与工程学报，2006，25（6）：1240－1245.（ZHANG Chang-suo，LIYi，ZHAO Yang-sheng，et al.Study on Optimum Excitation Wave in Grout Quality Nondestructive Testing of Rock Bolt［J］.Chinese Journal of Rock Mechanics and Engineering，2006，25（6）：1240－1245.（in Chinese））

［13］张东方.锚杆锚固质量动力无损检测数值模拟研究［D］.郑州：郑州大学水利与环境学院，2010：31－54.（ZHANG Dong-fang.Numerical Study on Dynamic Nondestructive Detection in Anchorage Quality of Rock Bolts［D］.Zhenzhou：College ofWater Conservancy and Environmentof Zhengzhou University，2010：31－54.（in Chinese））

［14］吕丹丹.低频信号的锚杆动态响应特征研究［D］.石家庄：河北科技大学电气信息学院，2011：7－26.（LV Dan-dan.Study on the Low Frequency Signal Anchor Bolt of Dynamic Response Characteristics［D］.Shijiazhuang：College of Electric Machines and Electronic of Heibei Universityof Science and Technology，2011：7－26.（in Chinese））

［15］梁龙龙.应力波法在边坡预应力锚索（无粘结型）结构检测中的试验研究［D］.北京：铁道科学研究院，2007：10－35.（LIANG Long-long.Study on StressWave Method in Pre-stressed（non-bonded）Anchor Cable Structure Detection of Slope［D］.Beijing：Academy of Railway Sciences，2007：10－35.（in Chinese））

［16］马宏伟，吴 斌.弹性动力学及其数值方法［M］.北京：中国建材工业出版社，2000：1－152.（MA Hongwei，WU Bin.Elastic Dynamics and Its NumericalMethod［M］.Beijing：China Building Materials Industry Press，2000：1－152.（in Chinese））

［17］李新平，江 杰，鲁志鹏，等.应力波法锚杆加固无损检测的数值模拟分析研究［J］.岩石力学与工程学报，2005，24（增1）：4647－4652.（LI Xin-ping，JIANG Jie，LU Zhi-peng，et al.Numerical Simulation Analysis of Nondestructive Detection of Stress Wave in Anchorage Bolts［J］.Chinese Journal of Rock Mechanics and Engineering，2005，24（Sup.1）：4647－4652.（in Chinese） ）

（编辑：曾小汉）

�杆（索）端头断面中点接收到的应力波信号 Fig.5

stresswave signal on m idpoint of top section of rock bolt（cable）

Numerical Study on Dynam ic Testing of Anchorage Quality of Rock Bolt（Cable）by StressWave M ethod

DENG Dong-ping，LILiang，ZHAO Lian-heng
（College of Civil Engineering，Central South University，Changsha 410075，China）

Rock bolt（cable）iswidely used in slope reinforcement.To ensure rock bolts（cables）work effectively，the stresswavemethod is generally adopted to detectanchorage quality.Length of rock bolt（cable）and position of defective segment are twomain indicators of detection.In this research，dynamicmodel of stresswave of anchoragebody is established in ANSYS/LS-DYNA.The percussion effectof hammers on rock bolt（cable）is presumed to be equivalent to the collision between hammer with a certain speed v0and rock bolt（cable），and stresswave signal is gathered on midpoint of rock bolt（cable）top section.Feasibility of the numericalmodel is verified by comparing with the results of theoretical studies in examples.Moreover，the effectof elasticmodulus and excitation speed v0of hammer on stresswave signal is analyzed，and the accuracy of defective segment position detected by using stress wavemethod is studied.The applicability of two excitationmodes（excitation on top and excitation on top and bottom simultaneously）in the detection is compared.Results reveal that：（1）Increasing the elastic modulus of hammer only affects the initial stresswave signal，but has little effecton stresswave signal reflected once back from the bottom of anchorage body；while the increase of excitation speed v0of hammer is conducive to both the signals and is linearly proportional to the latter.（2）It is reliable to use stresswavemethod to detect the defective segment position of anchorage body，and the detection accuracy is higher when defective segment ismore complete.（3）Themode of excitation on top and bottom simultaneously shortens the time of stresswave signal reflecting the positions of section change and bottom of anchorage body，so it is conducive to engineering applications.

rock bolt（cable）；stresswave；numerical simulation；anchorage quality；defective segment；plumpness；excitation mode

TU45

A

1001－5485（2015）01－0062－08

10.3969/j.issn.1001－5485.2015.01.013

2013－08－27；

2013－10－22

教育部博士研究生学术新人奖项目（114801045）；湖南省研究生科研创新项目（CX2012B056）；贵州省交通运输厅科技项目（2010－122－020）

邓东平（1985－），男，湖南岳阳人，博士研究生，从事道路与铁道工程等研究，（电话）13975150476（电子信箱）dengdp851112＠126.com。