基于PCA神经网络和D-S决策的瓦斯传感器故障辨识
2015-06-09徐平安王其军任玉东
黄 丹,徐平安,王其军,2,任玉东,严 彬
(1.安徽理工大学电气与信息工程学院,安徽淮南 232001;2.淮南职业技术学院,安徽淮南 232001)
基于PCA神经网络和D-S决策的瓦斯传感器故障辨识
黄 丹1,徐平安1,王其军1,2,任玉东1,严 彬1
(1.安徽理工大学电气与信息工程学院,安徽淮南 232001;2.淮南职业技术学院,安徽淮南 232001)
针对瓦斯传感器故障诊断时,存在提取的样本数据空间维数大、诊断实时性差、诊断结论的识别能力低和存在不确定性的问题,提出了一种基于主元分析(PCA)-神经网络和D-S证据理论集成的故障诊断策略。使用主元分析方法对高维故障样本空间数据进行降维,再结合神经网络分类器进行故障模式识别。并且运用DS证据理论对神经网络分类器的故障诊断结果进行数据融合。仿真实验表明:该诊断方法改善了神经网络对瓦斯传感器故障诊断准确率的同时提高了诊断速度,并且降低了故障结论的不确定性以及提高了结论的识别与决策能力。
瓦斯传感器;故障诊断;主成分分析;神经网络;DS证据理论
0 引言
瓦斯气体浓度的监测是煤矿安全监测的重要指标之一。瓦斯传感器也就成了煤矿安全的重要仪器。目前我国煤矿井下大都使用带有载体催化元件的瓦斯传感器。但由于井下环境恶劣,导致瓦斯传感器的卡死故障、冲击故障、漂移故障、周期故障等常见故障频发。因此研究瓦斯传感器的故障诊断方法,对提高煤矿安全监测系统的可靠性有着极其重要的作用[1]。
目前在煤矿安全监测系统中常采用的诊断方法有粗糙集与证据理论的结合,粗糙集与神经网络的结合等。其中粗糙集在原始故障数据的预处理方面已经得到很好的运用,它在处理冗余数据有其长处,而不足之处在于对噪声的敏感。神经网络主要优势在于对噪声数据不敏感,不足之处在于存在训练时间过长、实时性差、过拟合、输出结论的不确定性等问题。D-S证据理论则可以降低不确定性,可以弥补神经网络输出的不稳定性,但D-S证据理论要求每个证据都是相互独立的,并且由于其计算量大容易引起组合爆炸的问题[2-3]。据此,针对瓦斯传感器的故障诊断,提出了一种基于主元分析(PCA)——神经网络和D-S证据理论集成的故障融合诊断策略。该策略首先针对故障数据空间维数大的问题,利用PCA对故障数据进行降维。然后将降维后的数据输入到神经网络,以此简化了神经网络结构,达到实时诊断的目的。神经网络选用的是概率神经网络,并与BP神经网络作了对比仿真实验。针对单一故障诊断方法存在准确性和可靠性不高,甚至可能还会出现误诊的情况,利用了D-S证据理论将经过PCA处理的概率神经网络和BP神经网络的故障诊断结果进行融合,进而获得最终可靠的诊断结果,避免误诊的现象。故障诊断模型如图1所示。
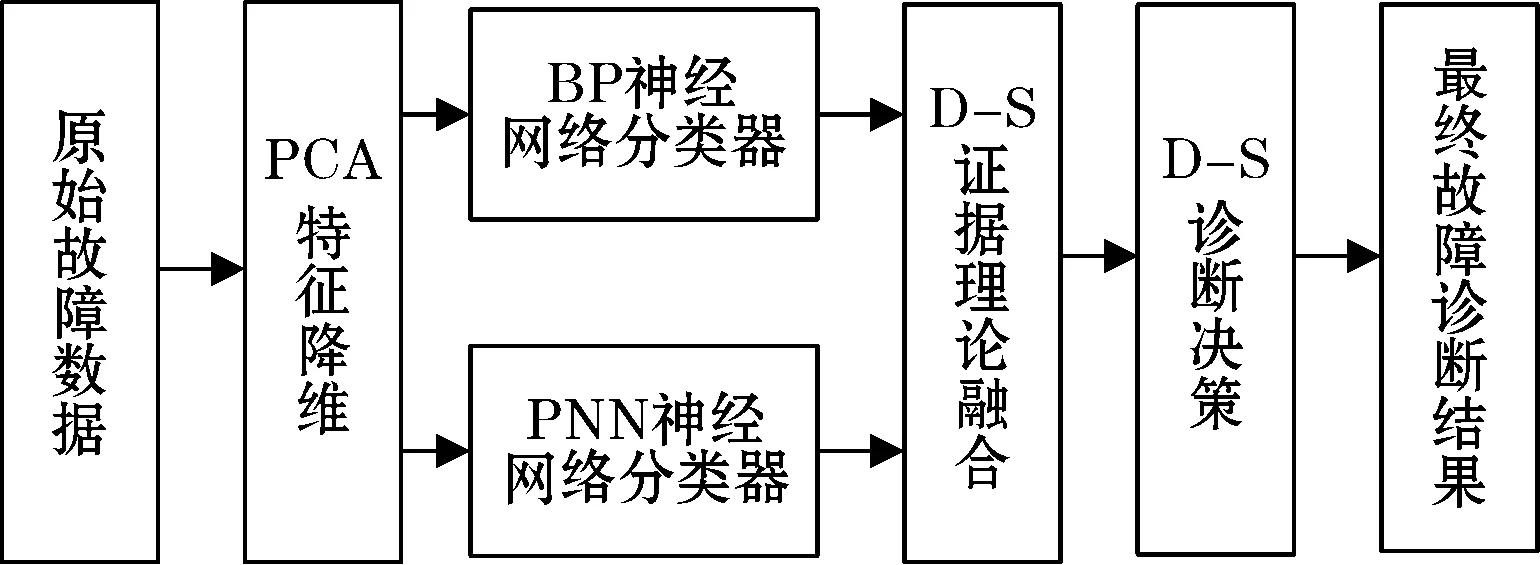
图1 故障诊断模型
1 故障诊断策略
1.1 主成分分析和神经网络
主成分分析方法(PCA)可对高维故障样本空间数据进行降维,将得到的低维故障数据输入到神经网络分类器进行故障模式识别。从而建立主成分分析和神经网络的结合。结合主成分分析,分别用概率神经网络和BP神经网络对瓦斯传感器的故障进行诊断,并且对二者的诊断效果做了对比研究。
1.1.1 主成分分析原理
主成分分析(Principle Component Analysis)[4]概念首先由Karl pearson在1901年引进,Hotelling在1933年对这个概念进行补充,将此概念由非随机向量推广到随机向量。它是最为常用的特征提取方法,通过对原始数据的加工处理,剔除冗余信息,简化问题处理的难度以改善对外界干扰的抵抗力。
在实际问题中会经常遇到需要研究多变量的情况,这会使得分析问题的复杂程度增加,因为变量较多时变量之间存在一定相关性。主成分分析就是重新组合原来具有一定相关性的众多变量,使其组成一组新的相互无关的综合变量来代替原来变量,并且按重要度从大到小排列。如果将选取的第一个线性组合即第一个综合变量记为X1,那么X1的方差Var(X1)越大,表示X1包含的信息越多。X1即为第一主成分,因为在所有的线性组合中所选取的X1是方差最大的。再考虑选取第二个线性组合X2,前提是第一个主成分不足以代表原来N个变量的信息,并且X1已有的信息不能出现在X2中,即数学表达式为Cov(X1,X2)=0 ,依此类推可以构造出第3,4,…,第N个主成分。由前所述易知主成分之间的方差是依次递减的,并且它们也都是不相关的。因此在实际的具体问题中可以挑选前几个最大主成分,这样有利于问题的分析和处理。
1.1.2 主成分分析计算步骤
设x=(x1,x2,……,xn)T为n维随机向量,则PCA具体求解步骤如下所示[5]:
(1) 将由具体的实际对象中所获得的数据组成样本矩阵X每一列为一个观察样本x,每一行代表一维数据。求解样本的协方差矩阵W;
(2) 计算协方差矩阵W的特征向量ui及相应特征值λi,其中i= 1 ,2 ,…,n;
(3)按照下式计算前m个主元的累积贡献率η(m),并按由大到小的顺序排列特征值。
累积贡献率用于衡量新生成分量对原始数据的信息代表度。当前m个主成分大于85%时即可将前m个主成分作为样本特征;
(4) 取前m个较大特征值对应的特征向量构成变换矩阵AT:
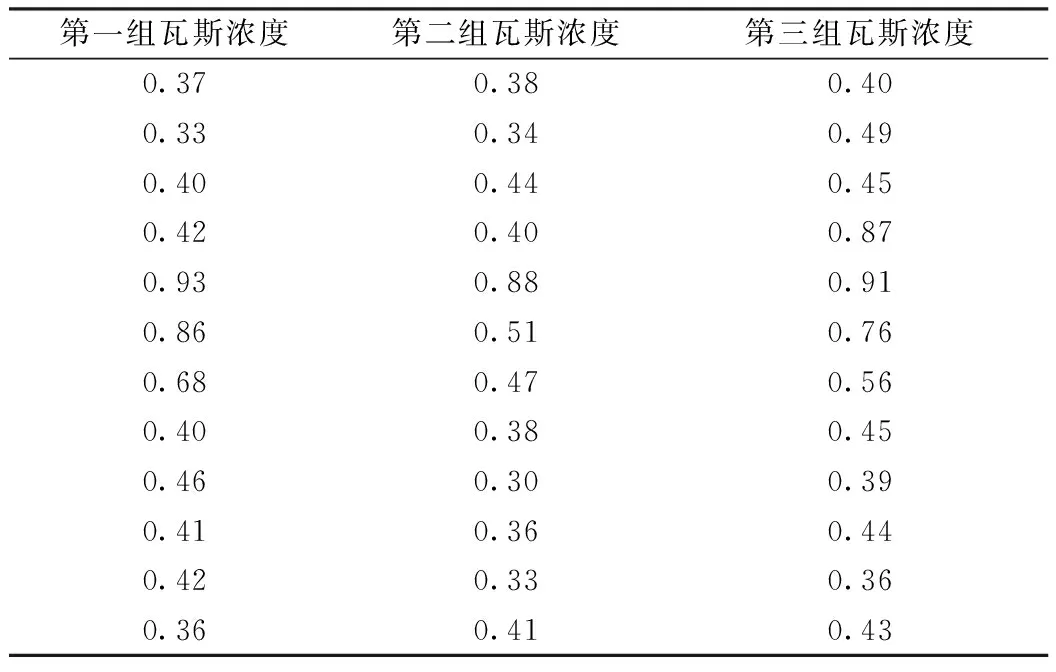
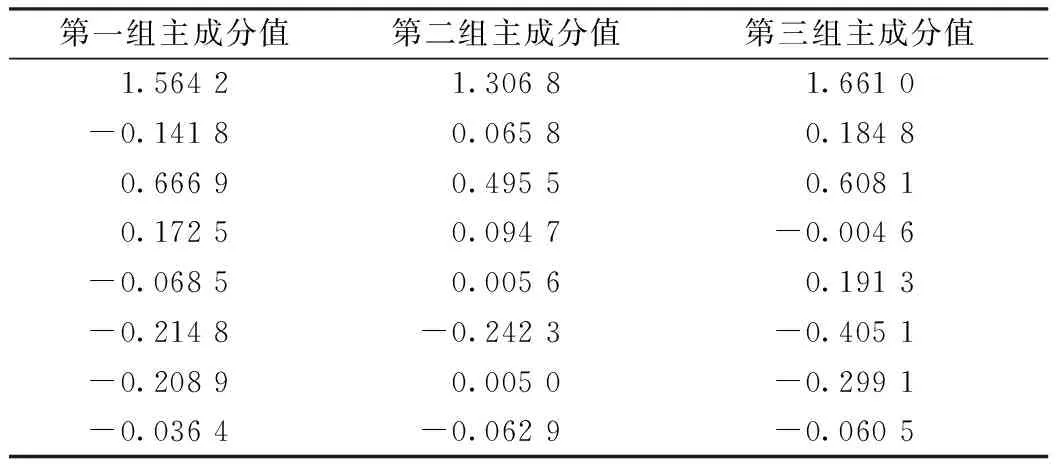
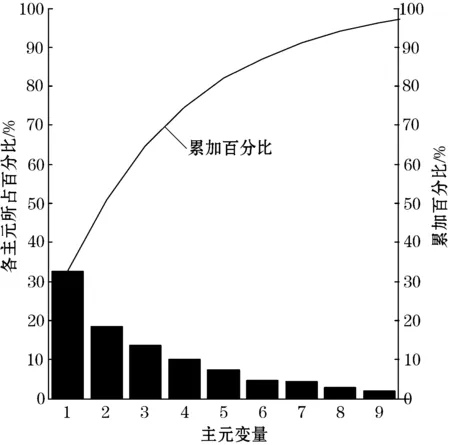
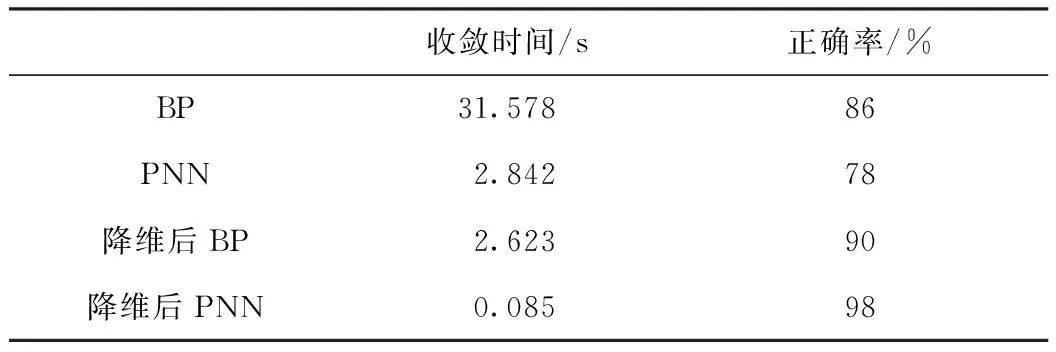
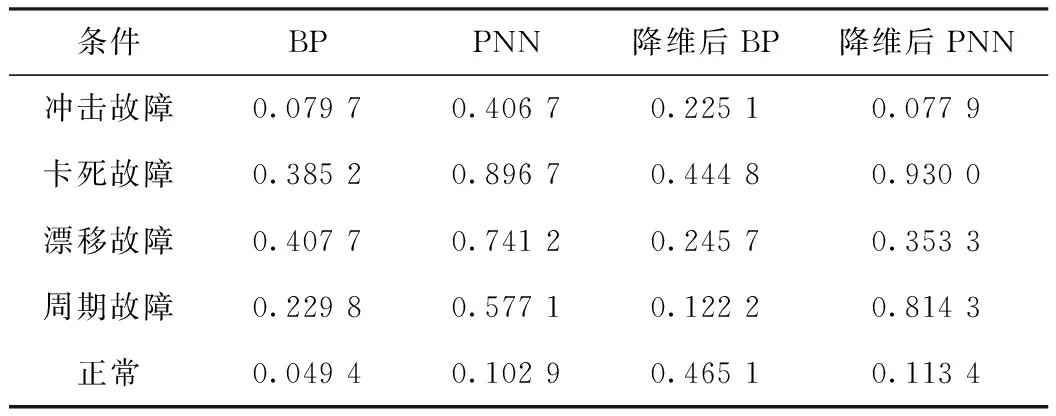
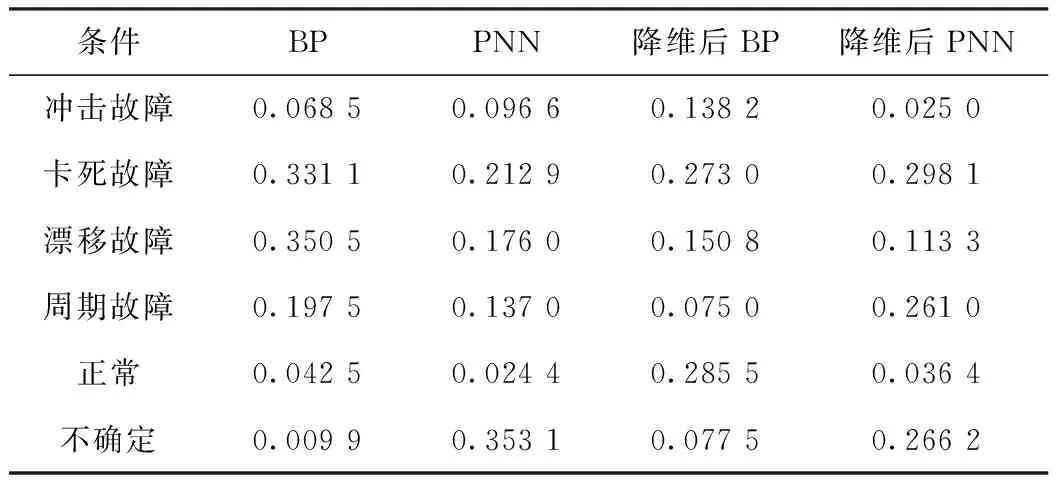
AT= (u1,u2,…,um),m (5) 通过Y=AX计算前m个主成分,达到降低维数的目的。 1.1.3 概率神经网络 概率神经网络(PNN),是D.F.Specht博士首先提出的。它是基于Parzen窗的概率密度函数估计方法与Bayes分类发展而来的并行算法。PNN是一类结构简单、训练简洁、应用广泛的人工神经网络。在解决分类问题的实际应用中,PNN的优势在于用线性的学习算法来完成非线性学习算法所做的工作,同时保持非线性算法的高精度等特性[6]。 概率神经网路属于前馈型神经网络,它是由径向基函数网络发展而来。Spread为径向基函数的扩展系数,Spread值越大其输出结果越光滑,但过大也会导致数值计算上的困难。在概率神经网络分类时,当Spread值较大时它构成训练样本的临近分类器,而当Spread值过小时它则构成了最邻分类器。PNN的层次模型总共有4层即由输入层、模式层、求和层以及输出层构成。其基本结构如图2所示。输入层将输入样本的特征向量传递给模式层的各个神经元,输入层神经元个数与输入样本矢量的维数相等。模式层神经元总数等于参加样本训练的样本数,它将输入层传递来的特征向量进行叠加计算,并通过非线性函数转化后输出给求和层。求和层则只是将属于某类的概率进行累计。输出层从求和层输出的结果中选择最大的,其对应的状态模式即为分类结果。 图2 概率神经网络基本结构 1.1.4 BP神经网络 目前在神经网络中BP神经网络已被广泛用,其结构一般由输入层,隐含层,输出层组成[7]。BP神经网络是多层前馈型神经网络,学习算法由正向传播和反向传播组成,其中反向传播时权值按Delta学习规则进行调整。在前向传递中依次按式(1)计算各层的输入输出直到输出层。 y=f(wi) (1) 式中:wi为某一层第i个节点的激活值;θj为阈值;xj为输入信号;wij为第i节点与第j节点的连接权系数;yi为某一层第i个节点的输出值。 反向传播则是根据期望与实际输出之间的误差调整权值和阈值[8]。权值的调整公式见式(2): (2) 式中:E为神经网络期望输出与实际输出的误差;η为学习速率。 1.2 D-S证据理论 1.2.1 D-S证据理论的合成规则 D-S证据理论的基本概念由基本概率分配函数M(A),信任函数Bel(A)以及似然函数PI(A)构成[9]。D-S合成规则是在给定几个同一识别框架上的基于不同证据的概率分配函数,如果这几组证据不是完全冲突,那么就可以利用该合成规则计算出一个概率分配函数,这个概率分配函数就可以作为这几组证据的联合作用下产生的概率分配函数。D-S合成规则是一个反应证据联合作用的规则。其合成公式如式(3)所示: (3) 式中:Mi(Ai)为同一识别框架U上的概率分配函数;Ai为焦元,即若A⊆U且m(A)>0,则称A为焦元;K为标准化因子,若K≠0上式有意义,存在合成后的概率分配函数,若K=0则上式无意义,原先的概率分配函数之间矛盾[10]。 1.2.2 D-S证据理论的诊断决策 计算得到每一个诊断命题和不确定性的概率分配函数,就可以由以下规则得到诊断结论[11]。 规则1:判断的故障类型应具有最大的概率数,并要大于某一阈值a,这里a取0.5。 规则2:判断的故障类型与其他类型的概率数之差要大于某个门限b,这里b取0.2。 规则3:不确定故障概率数要小于某个门限c,这里c取0.2。 规则4:判断的故障类型概率数要大于不确定性函数值。 1.2.3 D-S证据理论的融合诊断模型 单一的故障诊断方法存在缺陷,往往会影响诊断结论的准确性和可靠性。针对瓦斯传感器的故障诊断,提出基于主成分分析(PCA)-神经网络和D-S证据理论集成的故障融合诊断模型。利用了经过PCA处理后的概率神经网络和BP神经网络对瓦斯传感器进行故障诊断,以及为了作对比分析将未经过PCA处理的概率神经网络和BP神经网络也同时对瓦斯传感器进行诊断,即采取的是多种故障诊断方法共同诊断的策略。然后利用D-S证据理论对这4组故障结论进行融合,最后根据诊断决策得出最终的故障诊断结果。 2.1 故障样本获取 选取的故障样本数据来源于KG9017A低浓度甲烷传感器在4种故障(卡死故障、冲击故障、漂移故障、周期故障)和无故障的状态下反复进行实验所获取的瓦斯浓度值。共记录了200组数据,5种状态下记录的数据各占40组,每组12个数据。 2.2 PCA特征降维 考虑到主成分分析是对有一定相关性的变量重新进行线性组合和降维,并且各个故障状态下的数据显然具有一定的相关性,故利用PCA对5种数据分别进行降维以此来提高诊断的实时性。下面首先利用前面介绍的主成分分析计算方法对冲击故障数据进行降维。冲击故障数据的主成分比例分布图如图3所示,图形靠上方的曲线为累加线,是每个主成分累加后所占信息的比例线。由累加线可知前8个主成分所代表的信息已大于85%,故只需提取前8个主成分,即每组减少为8个数据作为故障样本即可。从而神经网络的输入层神经元由12个降为8个。例如选取在瓦斯传感器冲击故障下所得到的部分瓦斯浓度数据如表1所示,经过PCA降维后的数据如表2所示。 表1 选取3组冲击故障数据 % 表2 PCA降维后3组冲击故障数据 同理考虑到所提取的主成分,信息总和要大于85%以及神经网络输入层的个数的统一性,对剩下的4种状态(卡死故障,漂移故障,周期故障,正常)分别提取前8个主成分,即每组减少为8个数据作为新的故障样本数据,达到降维目的。并将降维后每种故障样本的40组数据,前30组作为故障样本训练数据,剩下的10组作为故障样本测试数据。 图3 冲击故障的主成分比例分布图 2.3 利用神经网络进行故障诊断 先利用瓦斯传感器4种故障和无故障下的200组原始数据分别设计BP神经网络分类器和概率神经网络分类器。每种故障样本为40组数据,每组12个数据,前30组用于训练,剩下的10组用于测试。神经网络的输入层用于接收故障样本每组12数据,故概率神经网络和BP神经网络输入层神经元个数为12个,输出层神经元个数都为5个,分别对应卡死故障、冲击故障、漂移故障、周期故障和正常5种状态。对于BP神经网络采用3层结构即输入层、隐含层、输出层。隐含层采用的激发函数为Sigmoid函数。而对于概率神经网络采用输入层、模式层、求和层以及输出层4层结构。其中输出层的激发函数改为purelinear函数,这是为了概率神经网络输出结果最终可以作为D-S证据理论的基本概率分配函数作铺垫。 然后用经过PCA降维后的200组故障样本数据再分别设计1个概率神经网络分类器和BP神经网络分类器,即每种故障样本为40组数据,每组已降维到8个数据,前30组用于训练,剩下的10组用于测试。以此来验证PCA的作用。概率神经网络和BP神经网络结构除输入层神经元个数为8个,其余同上。神经网络分类器诊断结果对比分析如表3所示。 表3 诊断结果比较 从表3中可知,利用PCA对各个故障样本数据进行降维处理后,神经网络的输入层神经元个数从12个减少为8个,概率神经网络和BP神经网络的收敛时间均有不同程度的降低,从而故障诊断速度得以提高。并且由于PCA具有对原始故障信息进行加工处理,剔除冗余信息,以改善对外界干扰的抵抗力的作用,故概率神经网络和BP神经网络降维后的故障诊断正确率均有不同程度的提高。另外概率神经网络的总体收敛时间要少于BP神经网络。 2.4 在诊断结论中运用D-S证据理论 将瓦斯传感器的5种状态即冲击故障、卡死故障、漂移故障、周期故障以及正常状态分别记为F1、F2、F3、F4和F5,且每个故障样本只属于这5种故障模式并且为单一故障,由此建立目标识别框架U={F1、F2、F3、F4、F5}。 BP神经网络分类器的输出数据不能直接作为D-S证据理论的概率分配函数必须进行归一化转换即 经转化后便可得到所需的概率分配函数值。 对于概率神经网络而言,将其输出层的竞争神经元的激发函数改为purelinear,则输出为测试样本属于不同故障模式的后验概率,对这组后验概率进行归一化得到的结果即可做为概率分配函数值。 瓦斯传感器常见故障类型总共5类(包括正常状态),从原始的故障数据中选取30个样本训练BP神经网络分类器1和PNN神经网络分类器1,再将这30个故障样本经PCA降维后训练BP神经网络分类器2和PNN神经网络分类器2。当瓦斯传感器发生卡死故障时,对故障传感器反复进行多组实验获取测量数据,将测量数据输入到训练好的BP神经网络分类器1和PNN神经网络分类器1,进行故障识别。再将降维后的测量数据输入到训练好的BP神经网络分类器2和PNN神经网络分类器2,同样进行故障的识别。这样便可同时得出4组故障诊断结论。表4为测量数据中的一组故障数据对应的4种神经网络分类器的诊断结果,经归一转化后所得到的概率分配函数值如表5所示。利用D-S证据理论的合成公式进行数据融合如表6所示。 表4 神经网络分类器的实际输出数据 表5 概率分配函数值 表6 利用证据理论合成公式进行数据融合 表4中虽然大部分神经网络分类器故障诊断的结论为卡死故障,但结论的区分性不高。例如降维后的BP神经网络输出值中卡死故障与正常状态对应的输出值比较接近,并且BP神经网络分类器还出现了误判的情况,即将卡死故障误诊断为漂移故障。表5是将各神经网络输出值经归一化处理得到的基本概率分配值,由于表4中神经网络分类器的输出值之间区分性不好、可靠性不高导致表5的各神经网络分类器的概率分配值基本偏低即可信度不高,利用D-S证据理论诊断决策无法作出故障诊断,故利用证据理论合成公式进行数据融合得到表6。由诊断决策可知表6最终的融合结果为卡死故障,并且表6融合后的不确定性与表5各神经网络的不确定性相比也大为降低。D-S证据理论的融合诊断方法解决了单一故障诊断方法存在误判的问题,给出了正确的故障诊断结论,将其运用于瓦斯传感器的故障诊断是可行的。 针对故障样本空间维数大、诊断实时性差的问题,提出了主成分分析法(PCA),对瓦斯传感器故障样本数据进行降维预处理。仿真结果表明:运用主成分分析方法实现了对故障样本空间的降维,在保留原始故障数据主要信息、改善神经网络故障识别率的同时,简化了神经网络结构,提高了故障诊断速度。 由于故障诊断结论的识别能力低以及结论的不确定性问题,在利用主成分分析对神经网络输入数据进行预处理的同时,对神经网络的输出结果运用D-S证据理论,降低了输出结果的不确定性并提高了输出结果的识别与决策能力。 [1] 黄凯峰,刘泽功,王其军,等.基于ASGSO-SVR模型的瓦斯传感器故障诊断.煤炭学报,王其军,2013(S2):518-523. [2] 高婷.数据挖掘和信息融合在煤矿安全监测系统中的研究:[学位论文].阜新:辽宁工程技术大学,2008. [3] 胡雅馨.基于粗糙集与证据理论的瓦斯传感器故障诊断技术的研究:[学位论文].阜新:辽宁工程技术大学,2009. [4] 苑津莎,尚海昆.基于主成分分析和概率神经网络的变压器局部放电模式识别.电力自动化设备,2013,33(6):27-30. [5] 唐宏宾,吴运新,滑广军,等.基于PCA和BP网络的液压油缸内泄漏故障诊断.中南大学学报(自然科学版),2011,42(12):3709-3713. [6] 王桂英,张世军,潘思尧,等.基于神经网络的变压器故障诊断方法研究.计算机测量与控制,2012,20(7):1760-1762. [7] 张学军.基于BP神经网络和D-S证据理论的火灾报警系统.仪表技术与传感器,2011(1):104-105. [8] 高峰,肖丽.基于改进BP神经网络的SRM 间接位置检测技术.仪表技术与传感器,2012(9):54-56. [9] 田海雷,李洪儒,许葆华.基于D-S证据理论和支持向量机的液压泵故障诊断技术.仪表技术与传感器,2013(5):81-83. [10] 陈淑娟.基于DS证据理论的多传感器数据融合危险预警系统:[学位论文].北京:北京化工大学,2010. [11] 王其军.瓦斯监测系统故障智能诊断技术研究:[学位论文].青岛:山东科技大学,2007. Fault Identification for Gas Sensor Based on PCA-neuralNetwork and D-S Evidence Theory HUANG Dan1,XU Ping-an1,WANG Qi-jun1,2,REN Yu-dong1,YAN Bin1 (1.School of Electric and Information Engineering ,Anhui University of Science and Technology,Huainan 232001,China;2.Huainan Vocational Technical College,Huainan 232001,China) For the problems existing in the gas sensor fault diagnosis such as the large space dimension of the sample data,weak real-time of fault diagnosis,poor identification ability of the diagnosis result and the uncertainty,fault diagnosis strategy was proposed based on principal component analysis (PCA) neural network and D-S evidence theory.The principal component analysis(PCA) was used to reduce the high dimension of the fault sample space data,combining the neural network classifiers to identify the fault mode,and the DS evidence theory was used for data fusion in the fault diagnosis results of the neural network classifiers.The simulation results show that the accuracy rate can be improved and the diagnosis speed can be increased by the use of the method.Furthermore,the uncertainty of fault conclusion can be reduced and the ability of the conclusion recognition and decision-making can be improved. gas sensor;fault diagnosis;principal component analysis;neural network;DS evidence theory 国家自然科学基金青年科学基金项目(51304007) 2014-07-07 收修改稿日期:2014-10-05 TP212 A 1002-1841(2015)03-0099-05 黄丹(1986—),硕士研究生,主研方向:煤矿安全监测、人工智能与故障诊断。E-mail:94609498@qq.com 徐平安(1989—),硕士研究生,主研方向:智能信号处理。 E-mail: xupingan11@ 163.com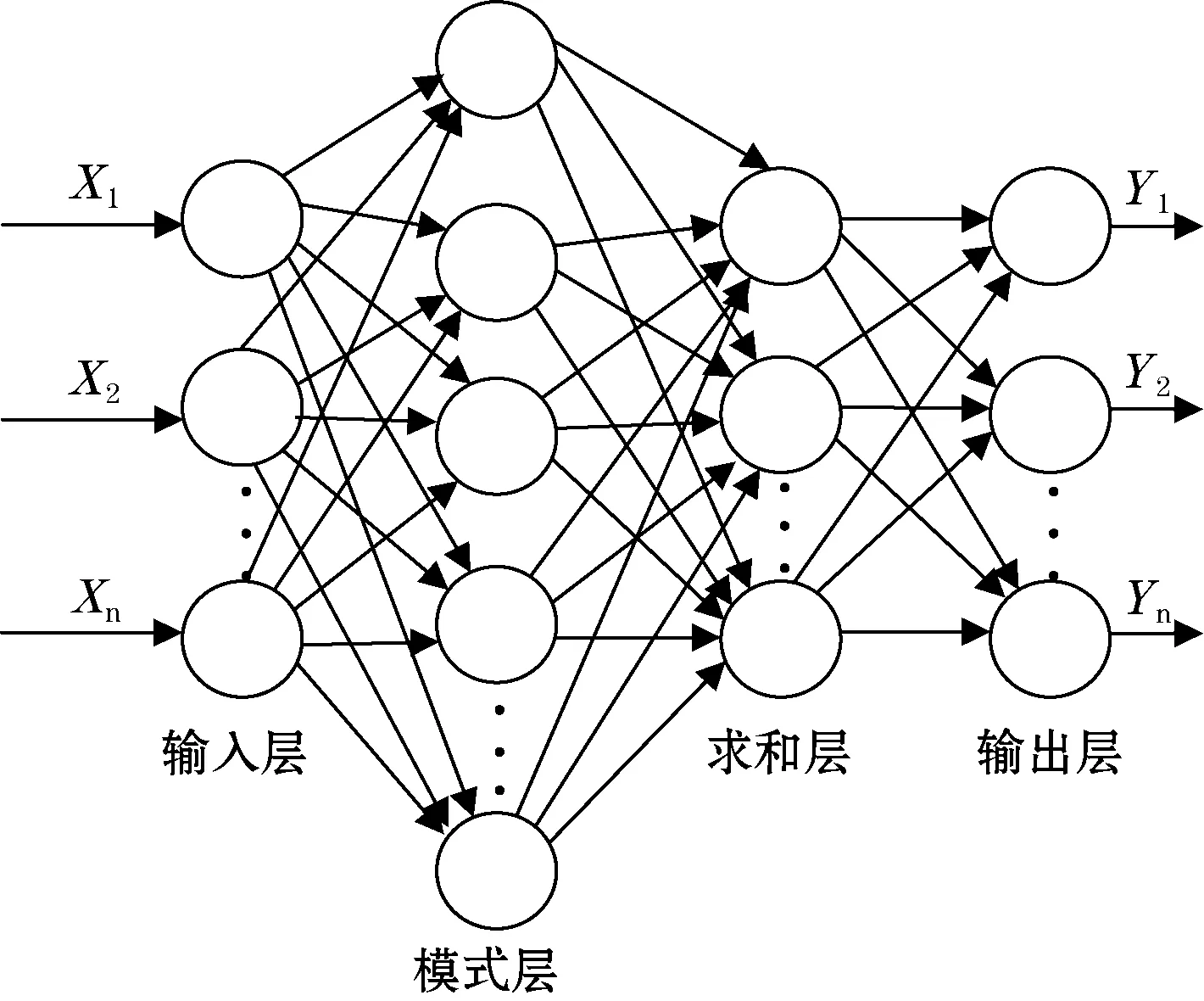
2 仿真研究

3 结论
