基于Hilbert-Huang变换的轨道车辆轴箱加速度信号分析

曹西宁，柴晓冬，郑树彬

(上海工程技术大学城市轨道交通学院，上海 201620)



基于Hilbert-Huang变换的轨道车辆轴箱加速度信号分析

曹西宁，柴晓冬，郑树彬

(上海工程技术大学城市轨道交通学院，上海 201620)

轨道不平顺是影响列车快速、安全运行的重要原因，同时轨道不平顺所引起的列车轴箱加速度变化能够反映轨道不平顺的状态信息。通过希尔伯特-黄变换(Hilbert-Huang transform，HHT)对采集到的列车轴箱垂向加速度进行分析，利用HHT能够准确地描述非线性、非平稳信号的时变特征，分析轨道不平顺引起轴箱加速度变化的主要特征频率分布。对轴箱垂向加速度信号EMD分解后时频分析，能够有效地对轨道存在的不平顺位置进行定位，实现轨道区段内一定程度的短波不平顺检测。

希尔伯特-黄变换;轴箱加速度;时频分析;轨道检测

0 引言

轨道不平顺是机车车辆振动的主要激扰源，直接影响到列车运行的平稳性、安全性和舒适性，是控制列车最高运行速度的主要因素之一[1]。轨道不平顺会对轮轨作用力产生影响，同时能够反映在列车轴箱加速度特征信息的变化上。为了保证列车运营的安全、提高旅客乘车的舒适性、合理利用现有轨道检测设备，国内外研究[2-4]在列车轴箱上安装加速度传感器获取轴箱加速度的变化信息，通过对轴箱加速度的不同分析来判断轨道的不平顺状态。

列车在轨道上运行时在轴箱上采集到的加速度信号是非平稳、非线性变化的信号。目前，对此类信号进行分析的主要工具有傅里叶变换、现代谱估计和小波变换等。傅里叶变换和现代谱估计建立在稳态信号处理基础之上，它仅能给出信号总体所包含的各种频率成分，不能解决何时出现何种频率的问题[5]。小波理论与以往其他研究方法相比，其频谱分辨率和时间定位精度都得到显著提高，但小波变换的有效性依赖于小波函数的选取，有时还会存在随着尺度增大，相应正交基函数的频谱局部性变差的缺陷，使其对信号的更精细分解受到限制。基于此，文中采用希尔伯特-黄变换方法对加速度信号进行分析处理，通过分析列车运行时由于轨道不平顺所引起的轴箱加速度频率变化特征，得出轨道不平顺频率(波长)-幅值时频分布。

1 希尔伯特-黄变换

希尔伯特-黄变换(Hilbert-Huang transform，HHT)[6]主要创新包括本征模态函数(intrinsic mode function，IMF)概念的提出和经验模态分解(empirical mode decomposition，EMD)的引入。经验模态分解依据数据本身的特征时间尺度进行信号分解，它是一种具有自适应性以及高效的数据处理方法，在处理非线性非平稳信号具有非常明显的优势。

EMD将一个复杂的信号分解为不同尺度特征的IMF之和，这些IMF要满足如下条件：

(1)极值点的数量和过零点的数量相等，或最多相差1个；

(2)任意时间点上，信号的局部极大值与局部极小值定义的包络均值必须是零。

对于原信号x(t)，可以按照如下步骤进行经验模态分解：首先找到x(t)上的所有的极大点以及极小值点，分别对其进行3次样条插值得到上包络线xmax以及下包络线xmin。包络线m1(t)的平均值定义为

m1(t)=[xmax(t)+xmin(t)]/2

(1)

利用原始数据减去均值以后得到

h1(t)=x(t)-m1(t)

(2)

如果h1(t)满足IMF的两个条件，则h1(t)即为第一阶IMF，否则将h1(t)当作新的信号重复以上步骤，即得

h12=h1-m11

(3)

重复以上过程k次，当h1k和h1(k-1)之间的方差满足终止条件的时候，那么h1k为1个IMF，即

h1k=h1(k-1)-m1k

(4)

假设c1=h1k，定义此时的残余分量为r1=x(t)-c1，重复以上过程，直到rn或cn满足终止条件时，原始信号的EMD分解结束，最后得到

(5)式中：rn为残余分量，代表信号的平均趋势。而各个IMF分量c1(t),c2(t)…cn(t),分别包含了信号从高到低不同频率的成分，且每个频率段所包含的频率成分随信号本身的变化而变化。

这样就得到了n个IMF分量和1个残余分量信号。

2 轴箱加速度信号采集

无论在直向的轨道上还是在轨道的转向处，轨道表面的波浪形磨耗、轨枕间距不平顺等现象都会引起轮轨作用力的巨大变化，特别是在列车速度很高的情况下，这些轨道缺陷不仅加速轮轨的磨损，甚至危及列车的运行安全。轨道不平顺会引起轴箱的振动，同时也能反映到轴箱加速度特征信息的变化上，通过对轴箱加速度的测量与其幅值、频率变化特征分析，能够有效地分析轨道的不平顺状态。

图1是轴箱加速度测量系统示意图，加速度传感器安装于列车轴箱上，轴箱加速度、列车速度、列车位置通过不同装置记录在车载采集设备上。图2是上海地铁2号线实验列车轴箱加速度传感器安装位置图，位于轴箱上的加速度传感器通过数据线与采集设备连接，采集列车运行时列车轴箱上加速度的变化信息。

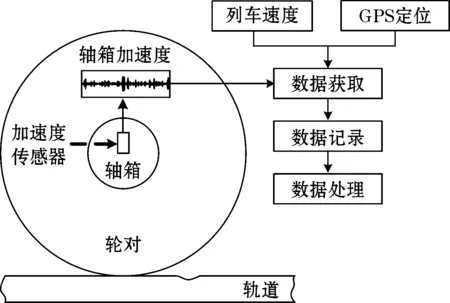
图1 轴箱加速度测量系统

图2 轴箱加速度传感器安装位置

3 应用于轴箱加速度信号分析

判断轨道状态的好坏，不仅要看它的各项指标是否满足规定要求，还要分析轨道不平顺信号的特征频率。轴箱加速度包含较大的带宽，同时含有可能存在的噪声以及多种轨道缺陷信息。通过滤波、时频谱等手段，可以对轨道的状态作1个相当可信的判断，所以采用希尔伯特-黄变换结合时频分析方法对列车运行时轴箱垂向加速度进行分析。

轨道车辆轴箱垂向加速度信号选用2013年9月上海地铁2号线龙阳路站与张江高科站之间一段49.2 m轨道列车采集数据。图3是根据列车采集到的轴箱垂向加速度数据经过低通滤波器滤波后画出的轴箱振动加速度图，图4是对轴箱垂向加速度数据处理后的频谱图。列车实验行驶速度为35.4 km/h，每m采集254点，采样频率为2 500 Hz。

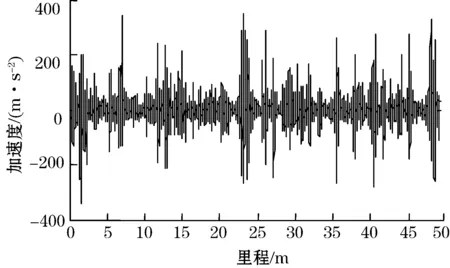
图3 轴箱垂向加速度信号

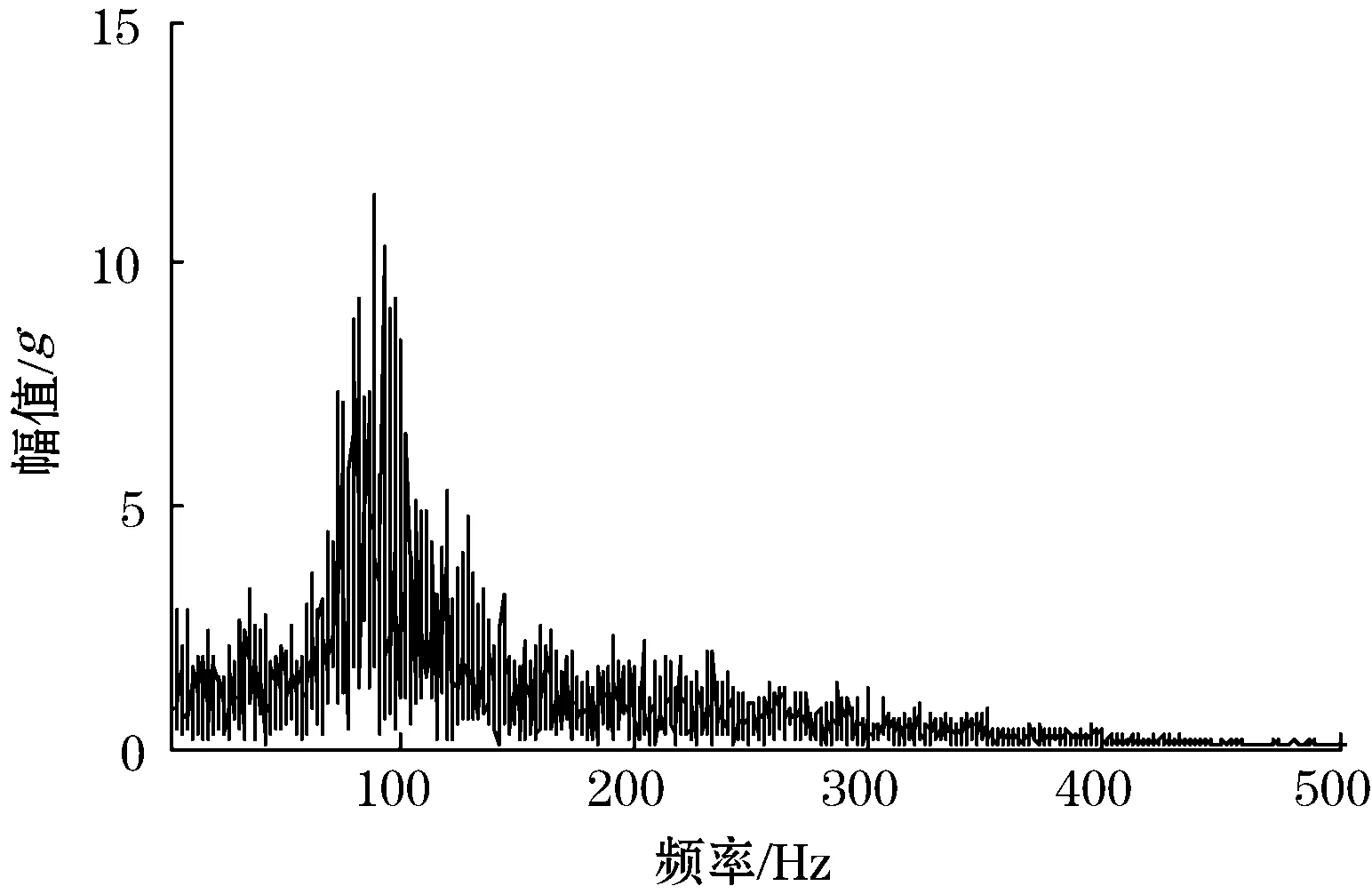
图4 轴箱垂向加速度频谱图

轨道不平顺波长在0.05～1 m的短波会引起行驶车辆的较大振动，特别是在列车轴箱垂向上的振动能很明显的体现[7]。这些轨道短波不平顺会导致列车的轴箱垂向加速度幅值上出现很大的突变。因此，在列车实验行驶速度为35.4 km/h时，0.05～1 m的短波所引起轴箱垂向的振动频率集中在9.833～197 Hz范围内。对轴箱垂向加速度进行EMD分解，图5所示为实测轴箱垂向加速度数据EMD分解结果，从上到下依次为C1,C2，…，res,为该信号依据EMD自适应地分解为12阶本征模函数(IMF)。图6中，从上到下依次为D1，D2，…，res，为各阶IMF的频谱图，显然在频率域中，EMD分解过程表现为从高频到低频的层层滤波，在整个频段内，0～300 Hz成分的振幅较大，在300 Hz以上的振幅较弱，这正是由于数据经过低通滤波器预处理后的效果。

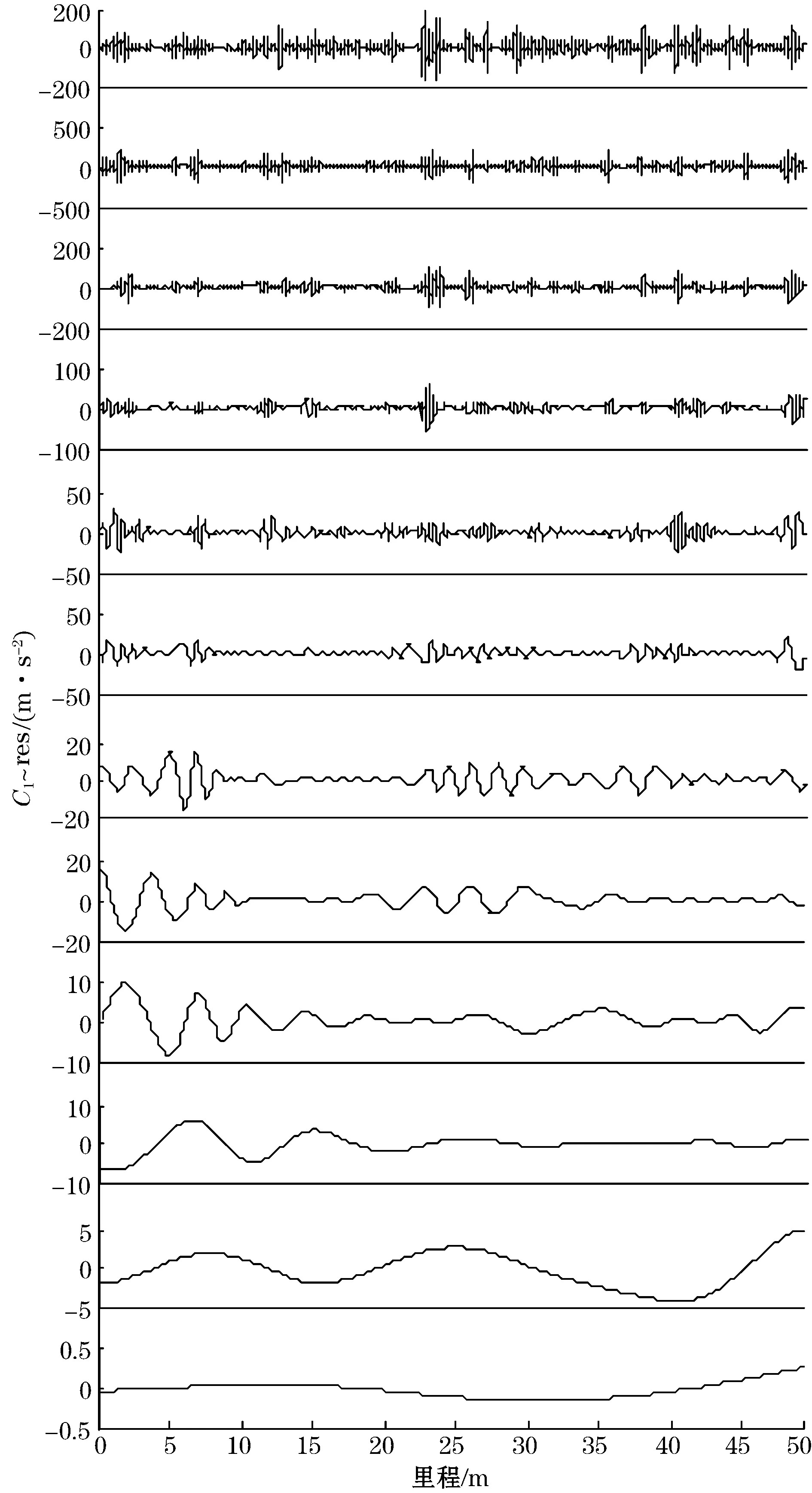
图5 轴箱垂向加速度EMD分解结果

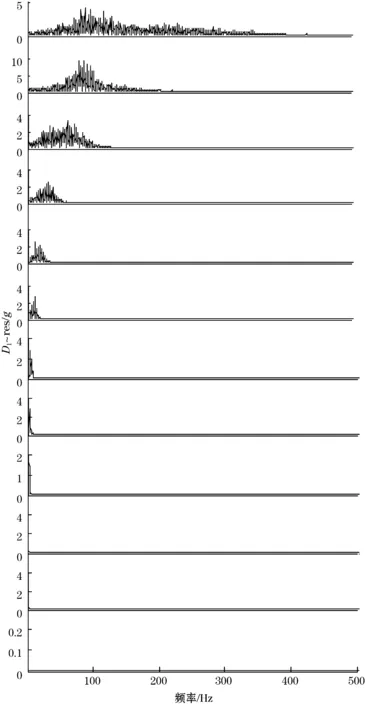
图6 各IMF分量频谱图

由于轴箱垂向加速度具有非平稳特征，数据采集过程可能出现某一时段信号强度大，信噪比较高，而在另一时段信号强度小，信噪比也较小的现象，若所采集的大部分信号强度低，则会严重降低数据质量[8]。Hilbert-Huang变换能够在时间序列中筛选信号强度大的时段数据进行处理，而舍弃信号强度小的时段数据，提高数据质量，同时能够表述信号的时频分布特性。

图7、图8所示是对图5所得的IMF经过Hilbert变换得到的时频谱。图7所示为轴箱垂向加速度信号的二维HHT时频谱图，图中各点表示能量，颜色越亮，表示能量越高，反之，能量越低。从图中可以看出信号的能量主要集中在100 Hz以内。图8所示为用Hilbert变换计算的三维时频谱，可见，时频谱具有很好的时频聚集性，瞬时能量谱直观地表明能量主要不均匀地分布在几个时间区间内(如图7、图8中1～6处)，能很好地区分能量随时间和频率的细微变化。

显然，在0～100 Hz频段内，整个时域能量比较集中，特别是在所取轨道测试段里程为7 m、12 m、23 m、26 m、36 m、48 m处能量值很大，频率分布主要集中在10～26 Hz范围内，相对应的这些轨道存在波长0.378～0.983 m的短波，这些轨道不平顺存在的点会在列车通过时引起轴箱垂向加速度明显的振动。通过与现场测试轨道区段实际情况进行对比，发现轨道存在缺陷的位置分布、波长范围与以上分析能够较好地吻合。在检测到的几百mm的短波类型中，包含轨道波浪形磨耗和轨枕间距不平顺，所以这些应为轨道工务维修的重点，通过对轨道相应的不平顺位置处维修能够及时有效保证列车的行车安全。

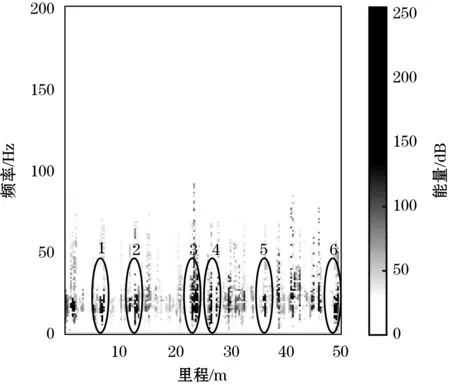
图7 垂向加速度信号的二维HHT时频谱

图8 垂向加速度信号的三维HHT时频谱

4 结论

文中首先介绍轴箱加速度测量系统构成，以及数据的采集、记录、处理等步骤。然后对经过预处理的实测列车轴箱垂向加速度信号分析，通过对其进行EMD分解后时频分析，能够有效地对轨道存在的短波不平顺分布进行定位，有利于铁路工务部门掌握轨道不平顺的波长、幅值分布情况，可以有针对性地对轨道存在的缺陷进行养护维修，提高作业效率，从而为城轨交通运营安全提供有力的保障。

[1] 李秋义.高速铁路无缝线路动力稳定性概率分析理论研究：[学位论文].长沙:中南大学,2003.

[2] WESTEON P F,LING C S,ROBERTS C,et al.Monitoring vertical track irregularity from in-service railway vehicles.Proceedings of the

Institution of Mechanical Engineers,Part F: Journal of Rail and Rapid Transit,2007,221(1): 75-88.

[3] WESTON P F,LING C S，GOODMAN C J,et al.Monitoring lateral track irregularity from in-service railway vehicles.Proceedings of the Institution of Mechanical Engineers,Part F: Journal of Rail and Rapid Transit,2007,221(1): 89-100.

[4] MORI H,TSUNASHIMA H,KOJIMA T,et al.Condition monitoring of railway track using in-service vehicle.Journal of mechanical systems for transportation and logistics,2010,3(1):154-165.

[5] COHEN L.Time-frequency analysis.New Jersey: Prentice Hall,1995：94-100.

[6] HUANG N E,SHEN Z,LONG S R,et al.The empirical mode decomposition and the hilbert spectrum for nonlinear and non-stationary time series analysis.Proceedings of the Royal Society of London Sertes A: Mathematical,Physical and Engineering sciences，1998,454: 903-995.

[7] MOLODOVA M,LI Z,DOLLEVOET R.Axle box acceleration: Measurement and simulation for detection of short track defects.Wear,2011,271(1) :349-356.

[8] 刘新厂，柴晓冬，郑树彬，等.惯性测量单元中加速度信号的去噪处理.仪表技术与传感器，2013(10):97-99.

Analysis of Acceleration of Train Axle Box Based on Hilbert-Huang Transformation

CAO Xi-ning,CHAI Xiao-dong,ZHENG Shu-bin

(College of Urban Railway Transportation,Shanghai University of Engineering Science,Shanghai 201620,China)

Track irregularity is an important reason for affecting the speed and safe operation of train,meanwhile the changing of train axle box acceleration caused by track irregularities can reflect the status information of track irregularity.Hilbert-Huang transformation was used to process the collected vertical acceleration of the train axle box and analyze main characteristic frequency distribution of the changing axle box acceleration caused by track irregularity based on its function of accurately describing time-varying characteristic of the nonlinear and non-stationary signal.Through time-frequency analysis of vertical acceleration signal of the axle box decomposed by EMD,the track irregularity position could be effectively located and the short wave irregularities within a certain degree can be detected.

HHT;axle box acceleration;time-frequency analysis;track detection

上海市自然科学基金(12ZR1412300)；上海市科委重点支撑项目(13510501300)；上海工程技术大学2012年度研究生科研创新专项项目(A-0903-13-01124)

2014-03-03 收修改稿日期：2014-10-11

TN911.7

A

1002-1841(2015)03-0092-04

曹西宁(1988—)，硕士研究生，研究方向为轨道交通检测技术。E-mail: sncxn@163.com 柴晓冬(1962—)，博士，教授，硕士生导师。研究方向为智能信息处理及轨道交通检测技术。