基于HPSO-RBF神经网络的瓦斯传感器故障诊断

王 婷，李国勇，吕世轩

(1.太原理工大学信息工程学院，山西太原 030024;2.太原理工大学,煤矿装备与安全控制山西省重点实验室，山西太原 030024)



基于HPSO-RBF神经网络的瓦斯传感器故障诊断

王 婷1，李国勇1，吕世轩2

(1.太原理工大学信息工程学院，山西太原 030024;2.太原理工大学,煤矿装备与安全控制山西省重点实验室，山西太原 030024)

针对瓦斯传感器常见故障，提出一种混合粒子群优化(HPSO)算法与径向基函数(RBF)神经网络相结合的传感器故障诊断新方法。文中首先采用HPSO算法对RBF神经网络模型参数进行了优化，在详细分析瓦斯浓度影响因素的基础上，建立了瓦斯浓度非线性预测模型。然后将瓦斯浓度预测结果与实际测量值相比较得到残差，并分析残差的变化趋势，从而实现对瓦斯传感器的故障诊断。实验结果表明，HPSO-RBF模型具有较高的预测精度，能够有效地诊断瓦斯传感器的故障状态。

瓦斯传感器;混合粒子群优化算法;RBF神经网络;故障诊断

0 引言

瓦斯传感器是煤矿瓦斯监测系统中的重要组成部分，监测系统通过它对矿井瓦斯浓度进行检测，因此其输出信号质量的优劣对煤矿生产安全程度及瓦斯监测系统性能会产生重大影响[1]。在井下高湿度、高粉尘、强电磁干扰等环境因素的长期作用下，瓦斯传感器经常会发生卡死、冲击、漂移等故障[2]，若不及时解决这些故障问题，会严重影响煤矿生产安全[3]。因此研究瓦斯传感器的故障诊断方法具有重要意义。

目前，瓦斯传感器的故障诊断方法主要有冗余法、多元回归分析法、时间序列分析法以及支持向量机、神经网络等智能方法。影响瓦斯传感器浓度的诸多因素是一种复杂的非线性关系，因此基于信息融合技术的神经网络成为主要的发展方向之一。其中，RBF神经网络是一种在曲线拟合、模式识别、图像处理、故障诊断等领域被广泛应用的神经网络，它不仅拓扑结构简单、非线性逼近能力强、收敛速度快，而且具有唯一最佳逼近的特性，但是其模型参数难以设置是应用研究的难点[4]。

针对RBF神经网络的模型参数优化问题，本文提出了一种混合粒子群优化算法，该算法将遗传算法中的交叉及变异操作引入到标准粒子群算法中，克服了粒子群算法易于陷入局部最优值的缺点。进而建立了基于HPSO-RBF神经网络的瓦斯浓度预测模型，并将其应用于瓦斯传感器故障诊断中。仿真与实验结果证明了该诊断方法的有效性。

1 RBF神经网络

RBF神经网络是一种3层前向神经网络，由输入层、隐含层、输出层组成，其结构如图1所示。RBF神经网络的基本思想是用RBF作为隐单元的“基”构成隐含层空间，隐含层对输入矢量进行变换，从而将低维的模式输入数据变换到高维空间内；而隐含层空间到输出层空间是线性映射，即通过对隐单元输出的线性加权和得到网络的输出。

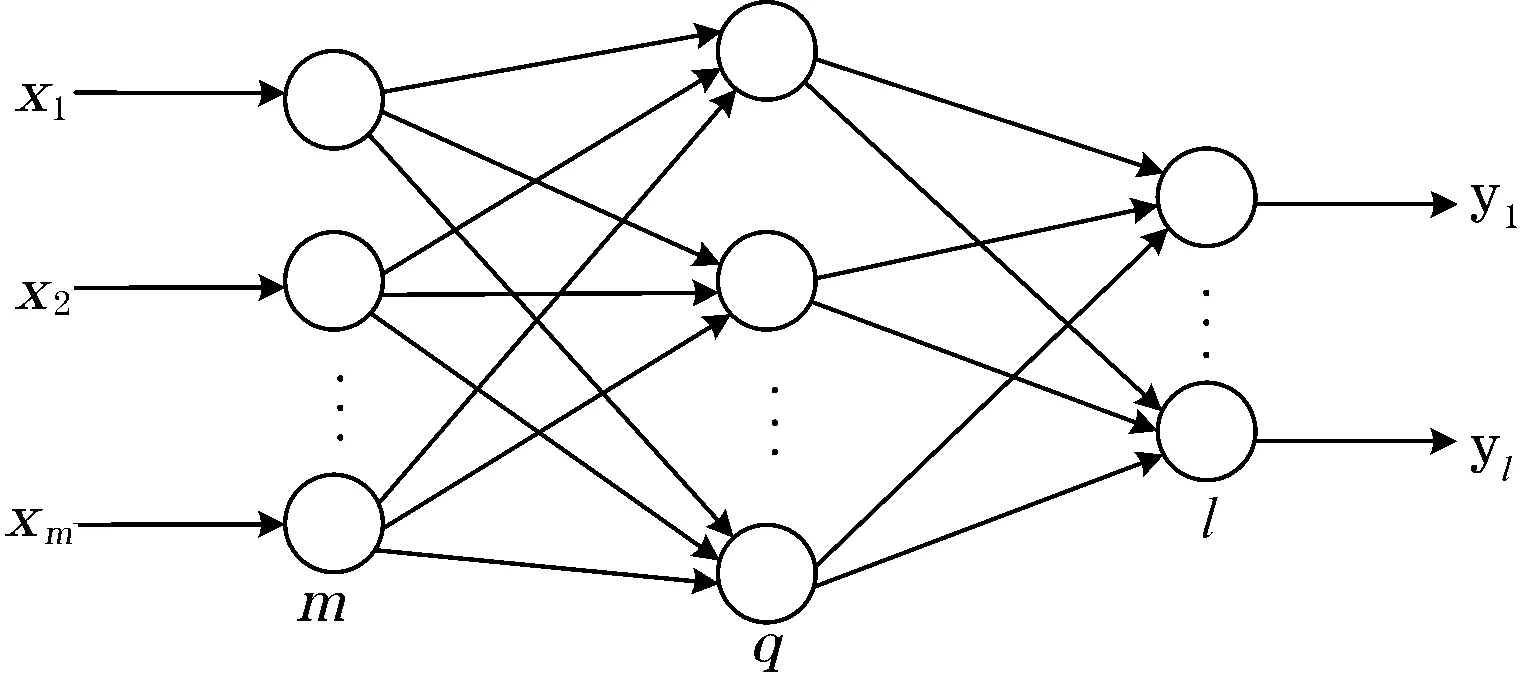
图1 RBF神经网络拓扑结构

假设RBF神经网络输入层、隐含层、输出层的节点数分别为m、q、l。RBF神经网络中常用的径向基函数是高斯函数，如隐含层第i个节点的输出可表示为

(1)

式中：i=1,2,…,q；ui是第i个隐节点的输出；σi是第i个隐节点的标准化常数；x=[x1，x2，…，xm]T为输入向量；ci=[ci1,ci2,…,cim]T为高斯函数的中心向量；‖x-ci‖为欧式范数。

RBF神经网络的隐含层到输出层实现ui(x)到yk的线性映射，如式(2)：

(2)

式中:yk是输出层第k个节点的输出；wki是隐含层到输出层的加权系数；θk是输出层的阈值。

2 混合粒子群优化算法

2.1 标准PSO算法

PSO算法是通过模拟鸟群的捕食行为来求解优化问题的。算法中每个粒子代表问题的一个潜在解，所有粒子都对应一个由适应度函数决定的适应度值，解的优劣程度由适应度值决定[5]。在每次迭代过程中，粒子通过跟踪个体极值pbest(粒子本身搜索产生的最优解)和群体极值gbest(种群中目前找到的最优解)来更新自身的速度和位置。

假设在一个D维的搜索空间中，由n个粒子组成的种群x=[x1,x2,…,xn]，粒子i表示为xi=[xi1，xi2,…xiD]T，粒子的速度表示为vi=[vi1，vi2,…viD]T，其个体极值表示为pi=[pi1，pi2,…piD]T，种群群体极值为g=[g1,g2,…,gD]T。对于每次迭代，其第d维(1≤d≤D)空间可根据以下公式更新：

(3)

(4)

式中:w为惯性权重；k为当前迭代次数；c1和c2为加速度因子，通常设置为2；r1和r2为分布于[0,1]区间的随机数；vid为粒子i的速度。

为防止粒子的盲目搜索，一般将粒子的位置和速度限制在一定的区间[-xmax,xmax]、[-vmax,vmax] 。

惯性权重w反映粒子继承先前速度的程度，实验证明，如果w采用线性递减惯性权重(LDIW)方法，将显著改善该算法的收敛性能。迭代公式如式(5)所示：

w(k)=wstart-(wstart-wend)×k/kmax

(5)

式中:wstart为初始惯性权重；wend为迭代至最大次数时的惯性权重；k为当前迭代次数；kmax为最大迭代次数。

2.2 HPSO算法

标准PSO算法具有算法收敛速度快、操作简单、易于实现等优点[6]，但PSO算法很容易陷入局部最优值，在迭代过程中，若粒子搜索到的当前最优解为一局部最优值，当所有的粒子都向该最优位置靠拢并收敛于该位置时，这些粒子将很难跳出局部最优，从而使算法出现早熟收敛现象[7]。因此，如何充分利用粒子群有价值的信息，实现粒子间信息的共享，使粒子以较快速度搜索到较优区域，同时保持种群多样性，是提高PSO性能的一个关键问题[8]。

遗传算法来源于生物进化思想，是一种借鉴生物界自然选择和自然遗传机制的随机搜索算法。在遗传算法中，通过选择、交叉、变异操作进行搜索，其全局搜索能力较强。其中交叉操作体现出信息交换的思想，变异操作可维持种群的多样性，减少早熟现象的发生。因此，本文利用两种算法之间的互补性，将遗传算法中的交叉和变异操作应用到粒子群算法中，得到一种整体性能更优的HPSO算法。

对于交叉操作，首先选择粒子使两两随机配对，然后按照一定的概率pc发生交叉。对于交叉的粒子xi、xj，计算过程如式(6)和(7)所示：

(6)

(7)

式中：α1、α2为[0,1]区间的随机数。

式(6)和(7)分别表示对粒子之间位置和速度的交叉操作。

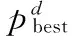
(8)

2.3 HPSO算法收敛性分析

假设适应度函数为f(x) ，HPSO算法搜索的过程是使适应度函数达到最小值，则结合适应度函数定义Lyapunov函数为

F(k)=f(gbest(k))-f(x*)

(9)

式中：gbest(k)是算法第k次迭代的群体最优值；x*为最优值。

可以看出，Lyapunov函数F(k)≥0。又因为在粒子群运动过程中式(10)必然成立。则根据Lyapunov定理可得HPSO算法是收敛的。

ΔF(k)=F(k)-F(k-1)=f[gbest(k)]-f[gbest(k-1)]≤0

(10)

3 HPSO算法优化RBF神经网络

RBF神经网络的模型参数对其性能有较大影响，本文采用HPSO算法优化RBF基函数的中心、方差以及网络的权值、阈值等参数。HPSO算法优化RBF网络的具体步骤如下：

步骤1：根据所给输入、输出训练样本集，设计RBF神经网络输入层、隐含层和输出层的节点数，确定网络的拓扑结构；

步骤2：粒子群初始化，根据神经网络的结构确定粒子总数N，初始化粒子的位置和速度，并设置加速度因子c1、c2，指定惯性权重w的初始值wstart与终止值wend，设定最大迭代次数kmax，以及交叉概率pc与变异概率pm；

步骤3：适应度值计算，根据适应度函数计算每个粒子的适应度值，并记录粒子的个体极值pbest和群体极值gbest；

步骤4：判断算法是否达到最大迭代次数或满足最小误差要求，若满足则迭代结束，输出全局最优解作为RBF神经网络相应的最佳参数；否则，继续进行下一步；

步骤5：粒子群的迭代，按照式(3)、式(4)更新粒子的速度和位置，并计算新粒子的适应度值，更新粒子的个体极值pbest和群体极值gbest；

步骤6：粒子群的交叉操作，将粒子两两随机配对并以概率pc按照式(6)、式(7)执行交叉操作；

步骤7：粒子群的变异操作，对粒子以概率pm按照式(8)执行变异操作，变异完成后，转到步骤3。

4 基于HPSO-RBF神经网络的瓦斯传感器故障诊断

4.1 HPSO-RBF神经网络瓦斯浓度预测模型

采煤工作面瓦斯传感器的设置如图2所示。图中上隅角设置瓦斯传感器T0，工作面设置瓦斯传感器T1，工作面回风巷设置瓦斯传感器T2，进风巷设置瓦斯传感器T3、T4，此外还有实时监测温度、风速、CO2浓度等传感器。

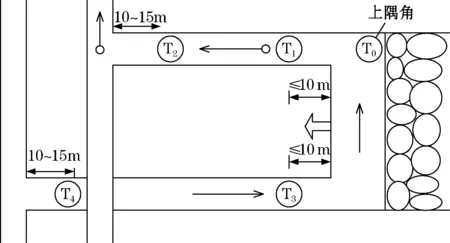
图2 某采煤工作面瓦斯传感器的设置

采煤工作面瓦斯传感器T1的浓度是在瓦斯浓度、风速、风量、温度及CO2浓度等相关因素综合作用下的结果，且T1的浓度与这些影响因素之间呈现高度非线性关系。因此，需对上述因素加以综合考虑来实现对T1瓦斯传感器浓度的高精度预测。

本文选取风速、温度、CO2浓度以及T0、T2瓦斯传感器的浓度作为RBF神经网络的输入变量，T1瓦斯传感器浓度作为输出变量，依据所提出的算法，进行仿真实验。

实验采用晋煤集团寺河矿瓦斯监测系统数据，取经过预处理和归一化处理后的36组样本数据进行RBF神经网络建模，取其中20组作为训练样本，16组作为测试样本。以RBF神经网络均方根误差RMSE(Root Mean Square Error)作为适应度评估函数，如式(11)所示：

(11)

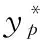
为检验预测效果，采用平均绝对误差MAE(Mean Absolute Error)和均方根误差RMSE指标对性能进行评价，MAE的定义如下：

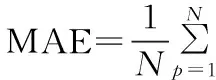
(12)

基于HPSO-RBF神经网络模型的瓦斯传感器浓度预测结果如图3所示，可以看出,HPSO-RBF神经网络模型能较好地逼近实际的测试输出数据。

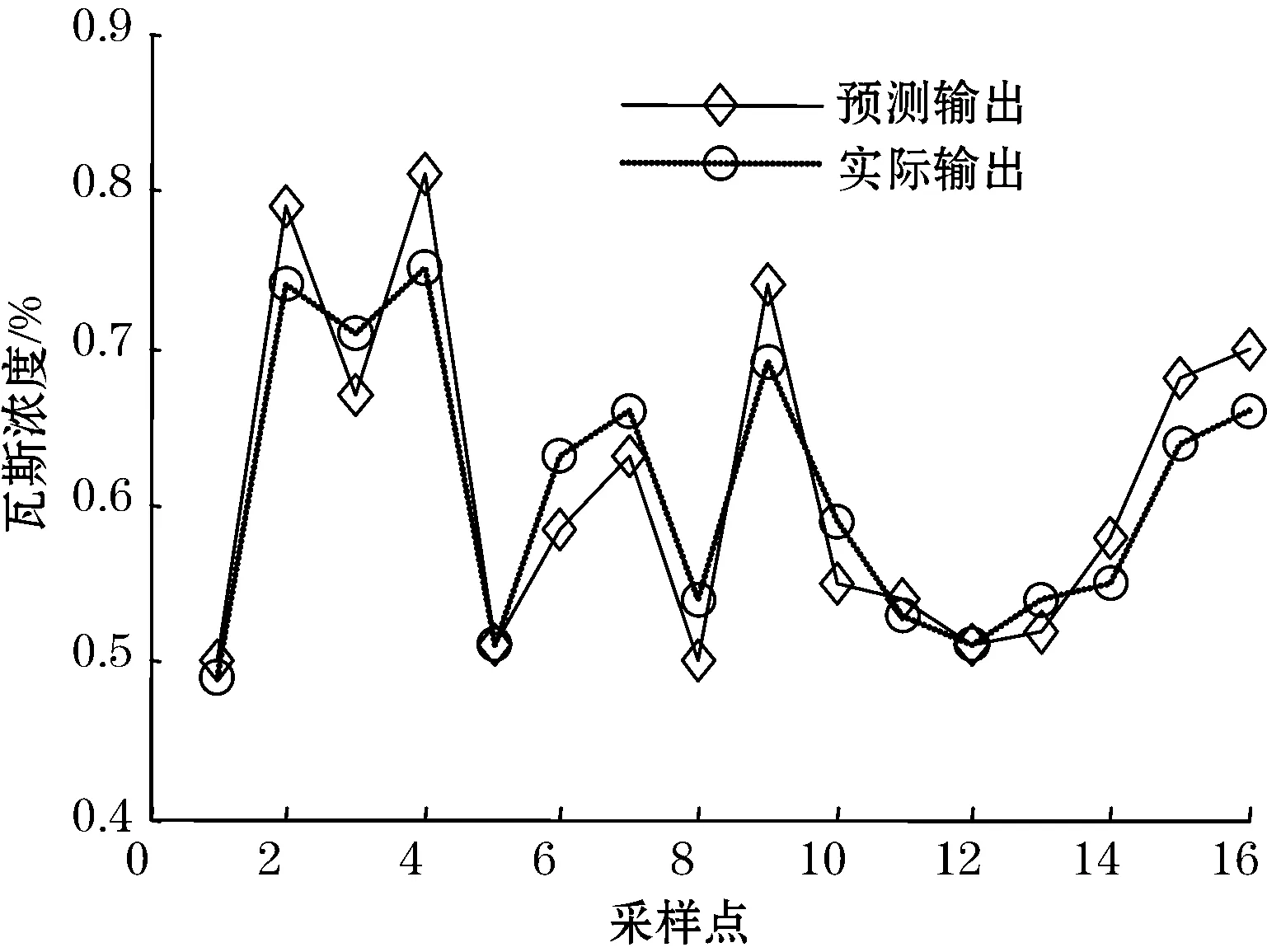
图3 HPSO-RBF神经网络的瓦斯浓度预测结果

为证明HPSO算法的优越性，表1定量比较了它与 RBF神经网络和PSO-RBF神经网络方法的预测性能指标。从表1可以看出，相比于其他2种方法，HPSO-RBF神经网络模型具有更高的预测精度。

表1 不同方法预测结果比较

4.2 故障诊断仿真分析

基于HPSO-RBF神经网络的瓦斯传感器故障诊断模型如图4所示。使学习训练好的HPSO-RBF神经网络模型在线工作，根据风速、温度、CO2及T0、T2等相应传感器测量值得到T1瓦斯浓度高精度预测值y*，并比较y*与当前时刻T1瓦斯传感器实际测量值y，得到残差σ，故障诊断系统则根据y*与y的残差及时地作出故障诊断，具体过程如下：根据经验性知识及实际数据的验证，设定阈值ε为0.79，若y*与y的残差绝对值|y*-y|≥ε，则判定T1瓦斯传感器出现故障；若y＊与y的残差绝对值|y*-y|<ε，则判定T1瓦斯传感器工作正常。

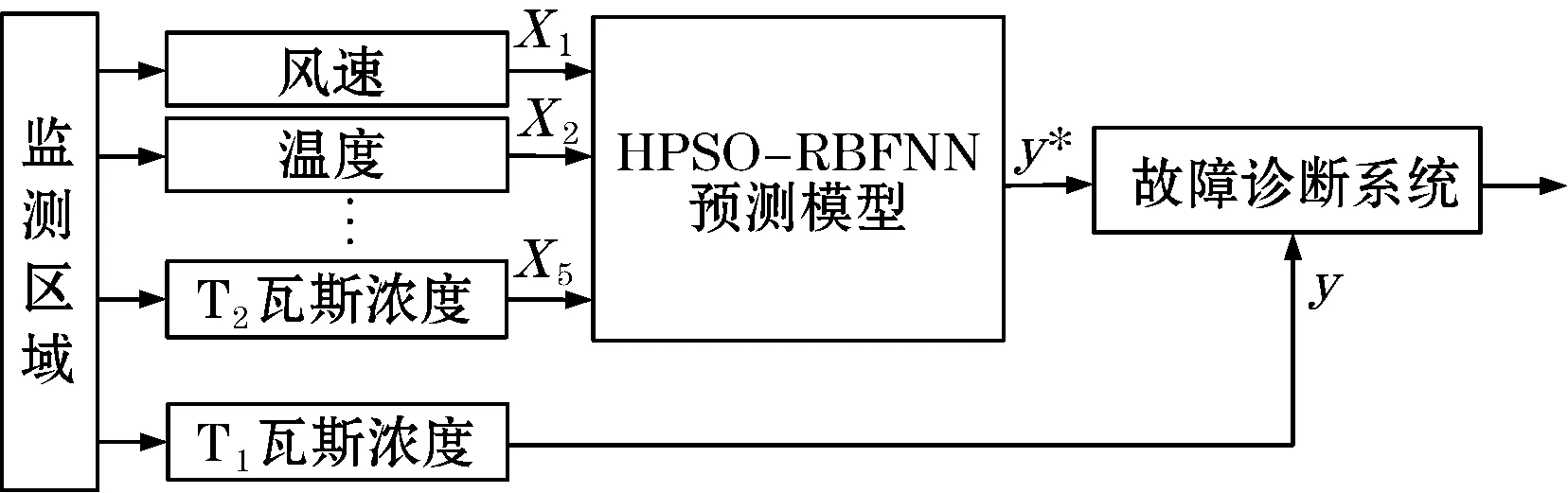
图4 瓦斯传感器故障诊断模型

图5为瓦斯传感器分别在正常、卡死、冲击、漂移4种状态下的残差信号变化曲线。从图5可以看出：瓦斯传感器处于正常工作状态时，残差信号变化很小，均值近似为零；瓦斯传感器从某一时刻开始出现卡死故障时，残差信号近似为y(t)=x(t)+Δ，出现值为Δ的恒偏差；瓦斯传感器在某一时刻出现冲击故障时，残差信号在短时间内严重超过所设定的阈值；瓦斯传感器出现漂移故障时，残差信号近似为y(t)=η·x(t)，呈现出斜率为η的恒增长的变化趋势。

当T1瓦斯传感器出现上述卡死、冲击、漂移故障时，预测值y*与实际输出值y进行比较，得到的残差超过设定的阈值，判定T1瓦斯传感器发生故障，诊断系统发出报警信号。通过仿真实验，证明该方法对瓦斯传感器常出现的故障诊断正确率较高。

5 结束语

本文提出了一种HPSO算法与RBF神经网络相结合的瓦斯传感器故障诊断方法。在HPSO-RBF神经网络的设计中，采用HPSO算法优化RBF神经网络基函数的中心、方差以及网络的权值、阈值等参数，克服了标准PSO算法易于陷入局部最优解的缺点，并建立了基于HPSO-RBF神经网络的瓦斯浓度预测模型。利用瓦斯监测系统采集的数据集训练并测试了HPSO-RBF神经网络的性能，预测结果表明该模型的预测精度要明显优于传统的RBF神经网络、PSO-RBF神经网络。将该预测模型应用到瓦斯传感器故障诊断中，实验结果表明本文提出的HPSO-RBF神经网络能够实时快速有效地诊断出瓦斯传感器常出现的卡死、冲击、漂移等故障，确保瓦斯传感器的工作可靠性，在煤矿安全生产中有较高的应用价值。

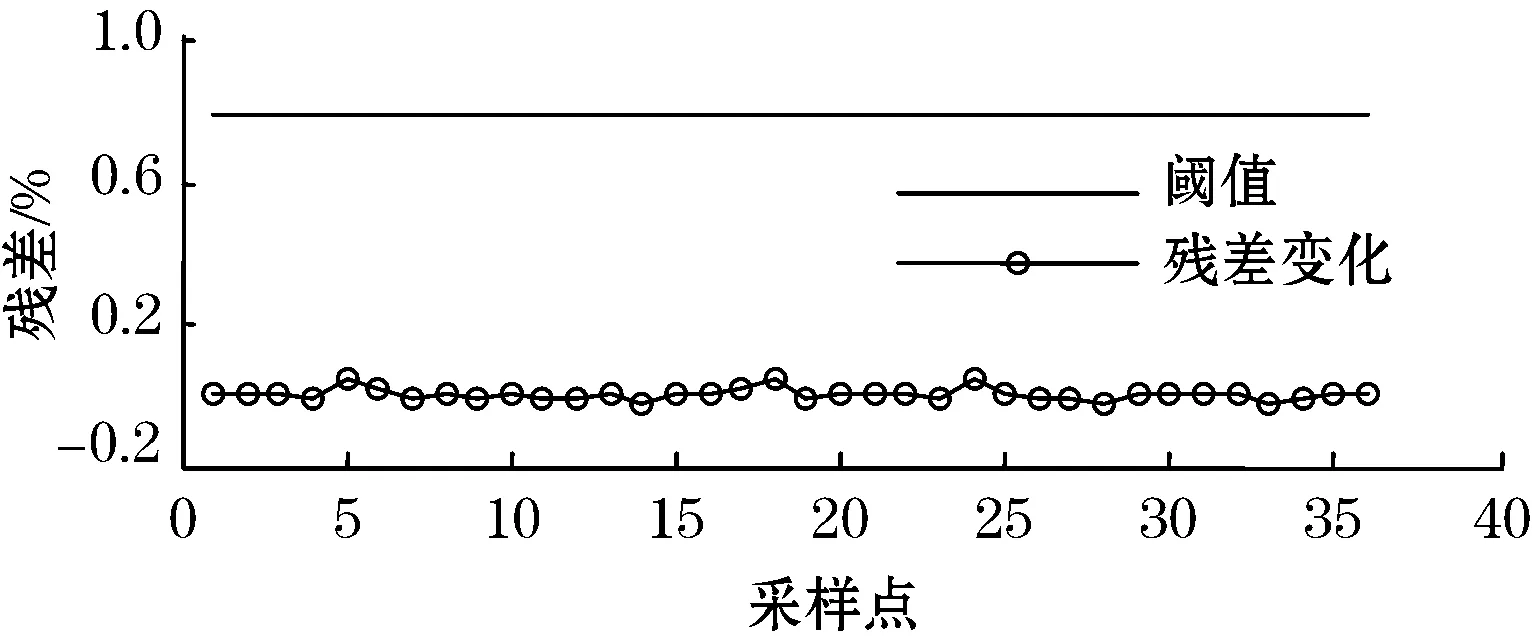
(a)正常工作状态

(b)卡死故障状态

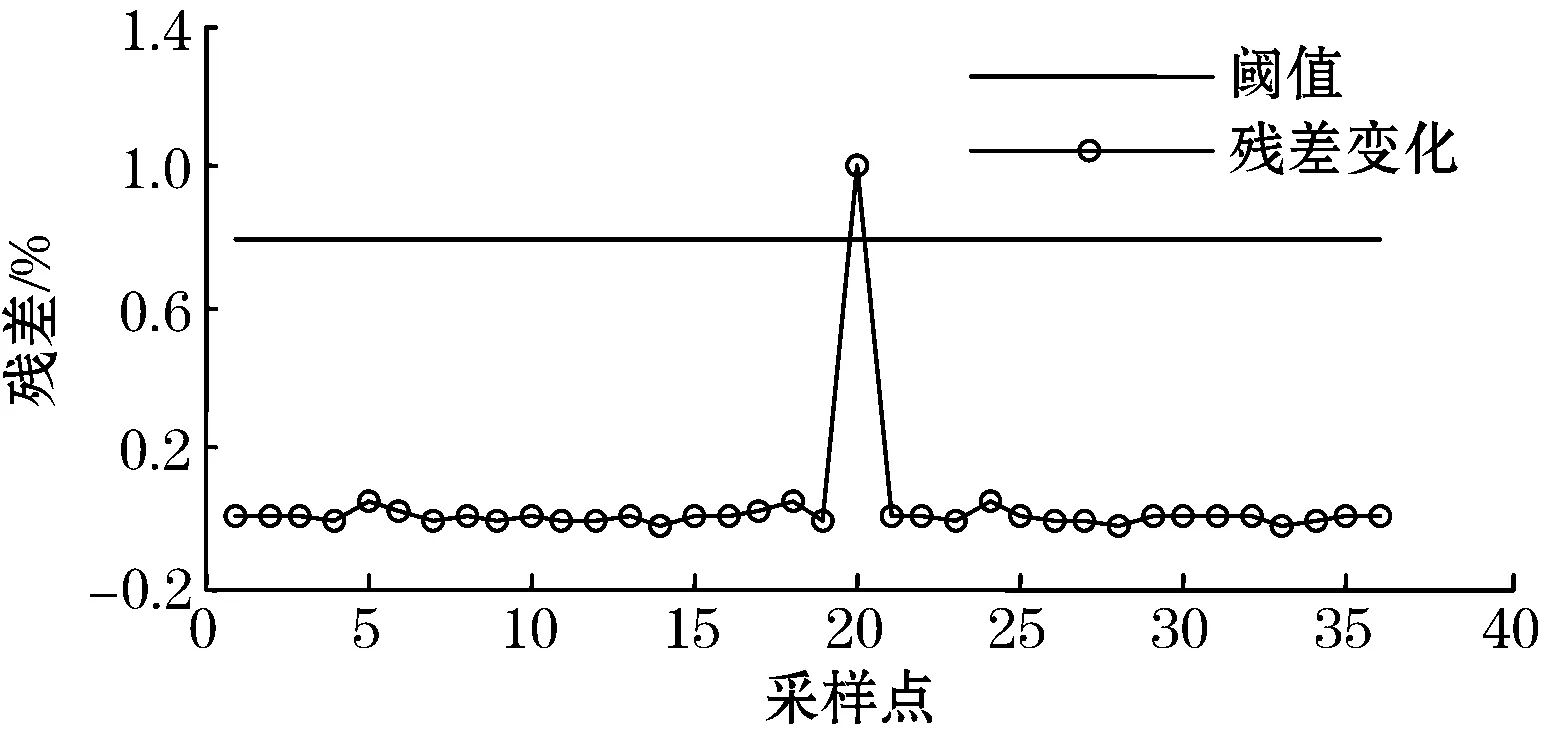
(c)冲击故障状态

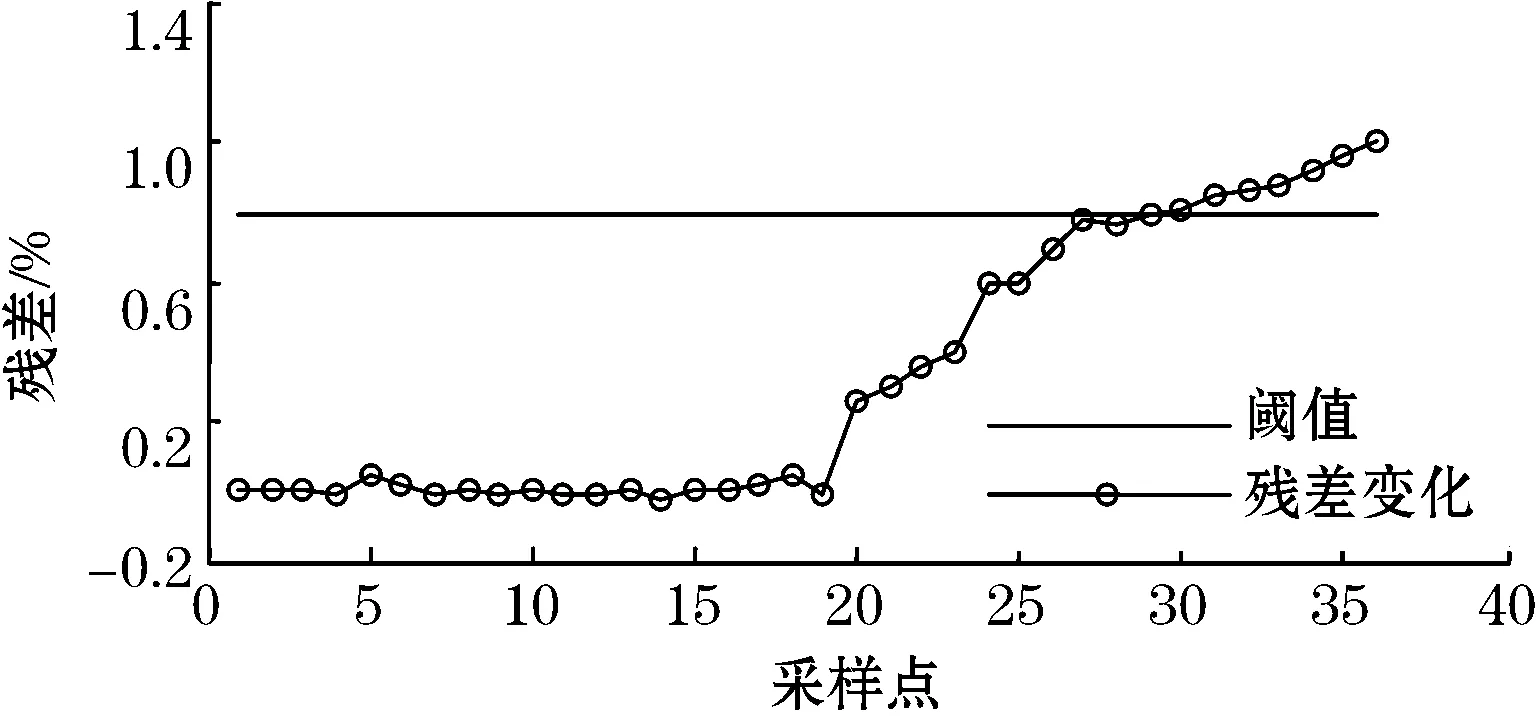
(d)漂移故障状态图5 瓦斯传感器4种状态下的残差信号变化曲线

[1] 周公博，朱真才，陈光柱.基于传感器网络的瓦斯传感器故障诊断.振动、测试与诊断，2010，30(1)：23-27.

[2] 王军号，孟祥瑞，吴宏伟.基于小波包与EKF-RBF神经网络辨识的瓦斯传感器故障诊断.煤炭学报，2011，36(5)：868-872.

[3] 刘玉珍，程政，蒋靖.基于ZigBee的井下巷道瓦斯监测系统.仪表技术与传感器，2012(9):49-51.

[4] KE M，ZHAO Y D，DIAN H W，et al.A Self-adaptive RBF neural network classifier for transformer fault analysis.IEEE Transactions on Power Systems，2010，25(3)：1350-1360.

[5] 李秀英，王光辉，韩志刚.基于高速收敛粒子群优化算法的非线性系统无模型预测控制.控制与决策，2012，27(5)：777-780.

[6] 郭通，兰巨龙，李玉峰，等.基于量子自适应粒子群优化径向基函数神经网络的网络流量预测.电子与信息学报，2013，35(9)：2220-2226.

[7] MODIRI A，KIASALEH K.Modification of real-number and binary PSO algorithms for accelerated convergence.IEEE Transaction on Antennas Propagation，2011，59(1): 214-224 .

[8] 刘黎黎，李国家，汪定伟.动态环境下带有非线性效益的复合粒子群优化算法.控制理论与应用，2012，29(10)：1253-1262.

Gas Sensor Fault Diagnosis Based on HPSO-RBF Neural Network

WANG Ting1,LI Guo-yong1,Lü Shi-xuan2

(1.College of Information Engineering,Taiyuan University of Technology,Taiyuan 030024,China;2.Shanxi Key Laboratory of Coal Mining Equipment and Safety Control,Taiyuan University of Technology,Taiyuan 030024,China)

Aiming at the common faults of gas sensor,this paper proposed a novel fault diagnosis method for gas sensor，which combined Hybrid Particle Swarm Optimization(HPSO)algorithm and Radial Basis Function(RBF)neural network.Firstly，the model parameters of RBF neural network were optimized by the HPSO algorithm.Through analyzing the influencing factors of gas concentration in detail,a non-linear prediction model for gas concentration was established.Then,the residuals between predicted results and actual measured values were calculated,and residual’s changing trend was analyzed,so as to realize fault diagnosis for the gas sensor.Experimental result indicates that the HPSO-RBF model has higher prediction accuracy and this method can diagnose faults of gas sensors effectively.

gas sensor;hybrid particle swarm optimization algorithm;RBF neural network;fault diagnosis

山西省自然科学基金资助项目(2011011011-1)

2014-02-13 收修改稿日期：2014-10-05

TP212

A

1002-1841(2015)03-0078-04

王婷(1989—)，硕士研究生，主要研究方向为预测控制、智能控制理论及其应用。E-mail:wangting_mail@163.com 李国勇( 1963—)，教授，博士，主要从事预测控制、故障诊断和智能控制理论与应用等方面的教学与科研工作。