一种二浮陀螺仪热仿真分析及试验验证

张沛勇，孙 丽，武丽花

(1.北京控制工程研究所，北京 100190； 2.天津航海仪器研究所，天津 300131)



一种二浮陀螺仪热仿真分析及试验验证

张沛勇1，孙 丽1，武丽花2

(1.北京控制工程研究所，北京 100190； 2.天津航海仪器研究所，天津 300131)

针对某卫星姿态控制系统中的重要测量部件二浮陀螺仪的精度及可靠性不断提高的要求，为了分析、掌握二浮陀螺仪的热设计及内部温度场分布对其精度和可靠性的影响，利用Ansys Fluent软件对二浮陀螺仪温度场进行仿真分析，得出其内部温度场分布情况，并与热真空试验数据进行比对，验证了二浮陀螺仪有限元模型及边界条件的准确性，根据仿真结果提出改善二浮陀螺仪热设计的优化措施.

二浮陀螺仪；热仿真.

0 引 言

二浮陀螺仪是卫星姿态控制系统中的主要测量部件之一，用于测量卫星本体相对惯性空间的运动角速度.随着卫星对二浮陀螺仪精度及可靠性需求的不断提高，二浮陀螺仪内部温度场对精度的影响凸显.之前，在进行热学特性的研究时，基本上只通过试验的方式对设计结果进行验证，对二浮陀螺仪自身的热学特性的分析很少，既不能做到提前识别存在的问题，又不利于产品的设计改进.当前，随着数值计算方法的不断发展，通过有限元分析方法可获得陀螺仪温度场的分布情况[1-4].本文通过Ansys Fluent有限元分析软件[5-6]对某卫星用二浮陀螺仪进行热仿真及分析，得到二浮陀螺仪内部的温度场分布情况，并通过热真空试验验证二浮陀螺仪热仿真模型的正确性，为后续二浮陀螺仪热设计提供参考数据.

1 二浮陀螺仪热模型的建立及仿真

1.1 二浮陀螺仪的热设计

二浮陀螺仪三大组件：浮子组件，传感器组件和壳体组件.浮子组件主要由陀螺仪马达、浮子框架和浮筒组成，其内部间隙充满氦气.二浮陀螺仪热环境复杂，陀螺仪既要加热保证浮液对浮子组件的浮力和重力完全相等，又要考虑陀螺仪内部马达的散热，因此二浮陀螺仪的热设计至关重要又有难度.

图1 二浮陀螺仪温控系统示意图Fig.1 Diagram of temperature control system of floated gyro

图1为二浮陀螺仪温控系统示意图.系统中加热元件采用带状薄膜加热片，缠绕在陀螺仪壳体上，通过传导对浮液加热.测温元件采用热敏电阻，布置在传感器组件上.感温元件采用两个热敏电阻串联，一个内热敏电阻布置在传感器组件上，另一个外热敏电阻布置在壳体外，用硅橡胶固定.上述元件和外部温控电路共同组成陀螺仪的温控系统，对陀螺仪的内部温度进行控制，进而达到浮液对浮子组件的浮力和重力完全相等，消除摩擦，提高陀螺仪精度的目的.

1.2 有限元模型的建立

二浮陀螺仪的几何结构比较复杂，几何模型的建立是前期的一项重要工作.建立的几何模型，既要保证计算模型与真实模型在结构、尺寸上的一致性，又要保证模型的计算效率.因而在建立模型前对二浮陀螺仪的结构模型进行了适当的简化.最终得到的有限元几何模型及网格模型如图2所示.

图2 二浮陀螺仪有限元几何模型及网格模型Fig.2 Geometric model and grid model of floated gyro

1.3 边界条件的确定

1)内热源的确定

二浮陀螺仪的内热源主要是陀螺仪马达功耗3.5 W.

2)主动温控热源

二浮陀螺仪的外热源为壳体外侧的加热片功率,根据测试数据陀螺仪在真空条件下各温度点加热片功率如表1所示.

表1 二浮陀螺仪稳态加热片功率

3)真空辐射边界条件

二浮陀螺仪外罩在真空下主要是辐射换热.陀螺仪外罩设为金属的半球发射率，吸收率与发射率相等，辐射环境温度为陀螺仪所处真空环境温度.

1.4 仿真结果

图3是真空环境为20 ℃时，陀螺仪温度场切片分布云图，切片位置分别是Y=0，X=0，Z=0.

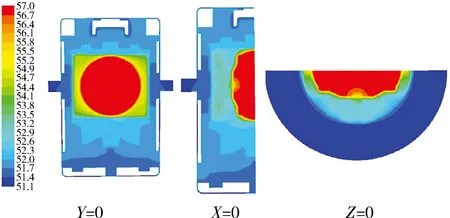
图3 陀螺温度切片分布云图Fig.3 Slices of temperature field distribution of floated gyro

图4是真空环境温度为20 ℃时，壳体与浮筒间陀螺仪浮液薄层的温度场分布云图.

图4 陀螺仪浮液薄层温度分布云图Fig.4 Slices of temperature field distribution of floated gyro oil lamella

1.5 仿真结果分析

由图3知：1)二浮陀螺仪温度场分布范围是51.1～57 ℃，温差为5.9 ℃，最高温部位是陀螺仪马达处，最低温位于陀螺仪法兰处.2)整个二浮陀螺仪的温度梯度主要集中在浮子内氦气处，温度范围53.5～55.5 ℃，温差为2 ℃，原因是氦气导热率小，其向外传热主要靠氦气的流动.

由图4知：1)陀螺仪浮液薄层内侧温度场分布范围是51.6～52.1 ℃，温度差为：0.5 ℃，浮液层四周是高温区域，马达轴正对的中间区域是低温区.原因是浮液层四周氦气流动速度快，传热快，而中间正对马达轴处氦气速度几乎为零.2)陀螺仪浮液薄层外侧温度场分布范围是51.5～51.9 ℃，温度差为：0.4 ℃，温度分布基本是两端高，中间温度最低.原因是中间正对陀螺仪的法兰，法兰通过陀螺仪支架导热，热量传递快导致中间温度低.

2 二浮陀螺仪热仿真的试验验证

2.1 热分析试验陀螺仪的设计

为了验证仿真模型的正确性，设计了热分析试验陀螺仪.热试验陀螺仪主要是在目前陀螺仪零件的基础上，在陀螺内部设置测温点[7]，通过测量测温点的温度，进而了解陀螺仪内部温度场的分布情况.

本设计中，共布置5个测点(浮子组件内部2个，浮子组件外部3个)，分别为：在浮子组件内部，安装陀螺仪电机的框架内壁(C1)、框架臂压块端面(C2)各1个测点；在浮子组件外部，浸于浮油内的左(C3)、右端部(C4)、壳体安装法兰上(C5)各1个测点.位置如图5所示.

图5 二浮陀螺仪内部测温点的位置图Fig.5 The position of thermal resistance in floated gyro

2.2 试验内容

在真空环境条件下，选取4个环境温度点，分别为10 ℃、20 ℃、30 ℃、40 ℃.试验时，将试验陀螺仪置于专用的密封罐内，利用真空泵实现真空状态，再将密封罐置于恒温箱内.试验陀螺仪的工作温度设置在50 ℃，实时测试各测温点阻值.

2.3 试验结果及分析

真空状态下，试验陀螺仪的工作温度设置为50 ℃ 保持不变，改变恒温箱的温度(即环境温度)，稳态时对应的各测温点的温度数据如表2所示.

表2 真空状态各环境温度下对应的各测点温度

从表2数据可见：1)温度最高点位于框架内壁上，比框架臂压块端面温度高0.1 ℃左右；2)浮子内温度比浮子外高1.5 ℃左右；3)环境温度为10、20、30 ℃时，表体内温度较为接近，相差0.2 ℃左右，当环境温度升至40 ℃时，表体内温度比30 ℃高4.5 ℃左右.

2.4 试验结果与仿真结果比对

在第1章仿真模型的基础上，改变环境温度，分别得到10 ℃、30 ℃、40 ℃时陀螺仪内部各测温点的温度值.

图6是真空环境温度为20 ℃时，陀螺仪内部各测温点的仿真温度值.

图6 真空环境温度为20 ℃时，二浮陀螺仪内部各测温点的仿真温度值Fig.6 The temperature values of measurement points inside floated gyro(vacuum ambient temperature is 20 ℃)

表3是真空环境温度分别为10 ℃、20 ℃、30 ℃、40 ℃时，陀螺仪热试验测温点数据与有限元仿真的温度数据对比情况.

表3 二浮陀螺仪热试验测点数据与仿真数据对比表

由表3知：通过有限元仿真得到的二浮陀螺仪温度场各测点的温度值与热试验得到的各测点的温度值相差很小，充分证明二浮陀螺仪热仿真模型准确性.

3 二浮陀螺仪热设计的优化

根据仿真及试验结果对二浮陀螺仪的热设计提出如下优化建议：

1)浮液的导热率低是温度梯度集中在浮液处的主要原因，因此在不改变浮液其他特性的情况下，提高浮液的导热率也是一种提高二浮陀螺仪内部温度场均匀性的有效措施;

2)根据仿真和试验结果，采取分区温控设计，调整加热功率分布，研制异型云图式加热片，也是进一步减小陀螺仪内部温度梯度的方法.

4 结 论

本文通过Ansys Fluent软件对二浮陀螺仪的温度场进行了仿真及分析，并通过热真空试验验证了仿真模型的正确性，同时根据仿真及试验结果提出了针对当前二浮陀螺仪热设计的优化措施，对后续二浮陀螺仪的热设计具有重要的参考意义.

[1] 李德才.基于流固耦合理论的长寿命陀螺仪浮子内部流场及温度场分析[J].中国惯性技术学报，2007，15(6)：721-723. LI D C. Analysis on temperature field and inner flow field of long-life gyro's floater with fluid-structure coupling theory[J].Journal of Chinese Inertial Technology，2007，15(6)：721-723.

[2] 卜石，刘娜.某型号液浮陀螺温度场分析[J].弹箭与制导学报，2006，26(4)：95-98. BU S,LIU N.The analysis on temperature field of a type of floated gyro[J].Journal of Projectiles, Rockets, Missiles and Guidance，2006，26(4)：95-98.

[3] 液浮陀螺温度场优化方法研究及实现[J].计算机测量与控制.2010,18(9)：2145-2147.

[4] APPEL N,HOLLAND J.Three dimensional finite element analysis of Inertial gyros[C]//AIAA Guidance and Control Conference.Washington D.C.:AIAA,1977：242-246.

[5] 韩占忠.FLUENT—流体工程仿真计算实例与应用[M].北京理工大学出版社.2004，185-265.

[6] 田杰，陈培譞，庄园.基于Fluent的ITER杜瓦的辐射换热分析[J].机械工程与自动化,2012,175(6):4-6 TIAN J, CHEN P X, ZHUANG Y. Thermal radiation analysis of ITER dewar by fluent[J].Mechanical Engineering & Automation,2012,175(6):4-6.

[7] 喻文焕 胡顺菊.液浮陀螺仪浮筒表面瞬态温度的确定[J].系统科学与数学,1983,5(3):216-222 YU W H, HU S J.Identification of transient temperature on the float surface of a floated gyroscope[J].Journal of Systems Science and Mathematical Sciences，1983,5(3)：216-222.

Thermal Simulation Analysis and Experiment Verification for a Type of floated gyro

ZHANG Peiyong1, SUN Li1， WU Lihua2

(1.BeijingInstituteofControlEngineeringBeijing100190,China；2.TianjinNavigationInstrumentResearchInstitute,Tianjin300131,China)

As one of the important measuring instruments in satellite attitude control system, the requirements for accuracy and reliability of floated gyro are increasing. In order to analyze the influences of thermal design and internal temperature field distribution of floated gyro on its accuracy and reliability, the internal temperature field is simulated and analyzed via Ansys Fluent software. By compared with the thermal vacuum test data, the accuracy of the finite element model and boundary conditions of floated gyro are verified. According to the simulation results, some optimization measures are proposed to improve the thermal design of floated gyro.

floated gyro； thermal simulation

2015-03-27

V249

A

1674-1579(2015)05-0039-04

10.3969/j.issn.1674-1579.2015.05.008

张沛勇(1978—)，男，工程师，研究方向为惯性姿态敏感器设计；孙 丽(1973—)，女，高级工程师，研究方向为惯性姿态敏感器设计.