月球上升段PEG参数自适应估计
2015-06-09王志文张洪华
王志文,张洪华
(北京控制工程研究所,北京 100190)
月球上升段PEG参数自适应估计
王志文,张洪华
(北京控制工程研究所,北京 100190)
针对月球上升器主动段制导中面临的上升器实际参数与制导计算机中存储参数不一致的问题,研究并提出PEG参数自适应估计的方法.通过分析,将对PEG制导有影响的参数如质量、质量流量、比冲、推力等转化为两个参数vex和τ,并利用加速度计输出对其进行估计.最后通过对使用参数自适应估计的PEG和未使用参数自适应估计的PEG的对比仿真,验证了PEG参数自适应估计的必要性和有效性.
参数;自适应估计;月球上升器主动段;PEG制导.
0 引 言
PEG(powered explicit guidance),即动力显式制导律,这种基于线性正切制导(linear tangent guidance)的最优制导,是在1970年为航天飞机项目提出来的,后来由NASA统一完善用于处理航天飞机大气层外的机动,包括正常上升,上升中止,离轨返回等[1].PEG实质上是两点边值问题的一个显式解,其优点在于它是闭环最优制导,有显式表达且形式简洁,可以减轻制导计算机的计算负担.
文献[2]中将PEG用于月球上升器上升主动段制导,研究了在存在初始位置、初始速度等状态偏差以及存在初始质量、质量流量、比冲等参数偏差和执行机构偏差的情况下,制导终端的高度、速度大小以及飞行路径角的偏差.文中指出,PEG作为一种预测校正的最优制导律,具有较好的鲁棒性,在存在如上的参数偏差的情况下,制导终端仍然较好地满足了要求.同时文章分析了这种结果的主要原因在于整个制导过程中上升器的实际参数和产生制导律的制导计算机中存储的相应参数是一致的,也即上升器实际参数“可观”.而在实际工程应用中,由于种种原因,在上升器上升主动段初始时刻,上升器实际参数和制导计算机中存储的相应参数往往是不一致的,也就是这两部分参数会有偏差.所以为了使得PEG制导终端状态满足要求,需要在PEG制导过程中在线估计上升器参数,并将估计的参数用于PEG制导律.
1 PEG制导律
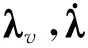
1)计算vgo
vgo,k=vgo,k-1-Δvs
(1)
式中vgo,k表示第k步的vgo,Δvs表示两步之间加速度计测得的速度增量.初始时,vgo为给定的一个值.
2)计算tgo
(2)
其中,F为推力大小,m为质量,Isp为比冲,g为地球重力加速度大小,tgo为制导剩余时间.定义
vex≜Ispg
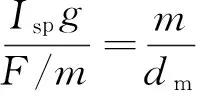
则式(2)可以写为
(3)
3)计算制导参数
(4)
(5)

rgo,k=rd,k-1-rk-vktgo-rgrav,k+rbias,k-1
S=λv·rgo,k,

(6)
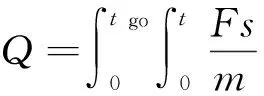
4)预测
预测终端速度
vp=v+vthrust+vgrav
预测终端位置
rp=r+vtgo+rthrust+rgrav
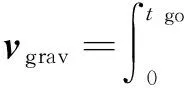
5)校正
vmiss=vp-vd
vgo(new)=vgo(old)-vmiss
其中vd为期望的速度,vgo(new)为更新后的速度增量,vgo(old)为当前的速度增量.若上述得到的偏差vmiss不满足预设的条件,则流程从第二步开始继续循环.
2 自适应估计原理
如前所述,实际上升器的比冲Isp,初始质量m0,质量流量dm,推力F等都会和制导计算机中存储的对应参数有一定偏差,自适应估计主要是利用加速度计输出对其进行在线估计,以使得二者之间的偏差趋向于零.
通过前面第二部分对PEG制导流程的分析,发现上述几个参数在PEG制导中的影响可以用τ和vex两个参数来替代,所以自适应估计的任务转化为对这两个参数进行在线估计[6].
F=ma=dmvex
(7)
(8)
令
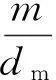

则有
(9)
此时,式(8)可以写为
取倒数
(10)
式(10)非常重要,它说明可以利用加速度计的输出a(t)来估计vex和τ0.而τ0和τ具有式(9)的关系,所以得到τ0也就可以计算出τ.
3 卡尔曼滤波方程
3.1 系统方程
上面已经得到参数自适应估计的重要公式(10),下面考虑用卡尔曼滤波的方法在线估计vex和τ0.令状态x
测量z
则状态方程
(11)
测量方程
(12)
式中v是测量噪声,R=E(v2).
(13)
离散化测量方程(12)有

Rk=E(vk2)
(14)
3.2 滤波方程
在上述分析的基础上,可以得到卡尔曼滤波方程[7]
k为卡尔曼滤波增益,由以下黎卡提方程得到
(15)
3.3 噪声等效转换
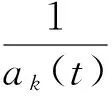
设实际加速度计的测量输出为ak+δak,加速度计的测量误差
(16)
从式(16)中可以看出
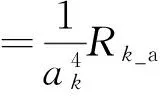
4 仿真分析
为了验证参数自适应估计的有效,分别对使用参数自适应和未使用参数自适应的PEG进行对比仿真.仿真中初始参数偏差如表1所示.

表1 仿真参数
对使用了参数自适应估计的PEG仿真发现,终端时刻高度、速度大小、飞行路径角等均满足要求,推力方向仿真曲线如图1所示,vex和τ的估计偏差如图2所示.可以看出,推力方向变化平滑,没有出现激烈跳变,且参数vex和τ均收敛到实际值.
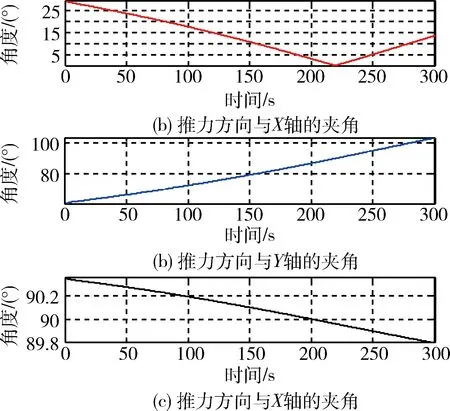
图1 使用自适应参数估计后的推力方向Fig.1 Thrustorientation with adaptive estimation
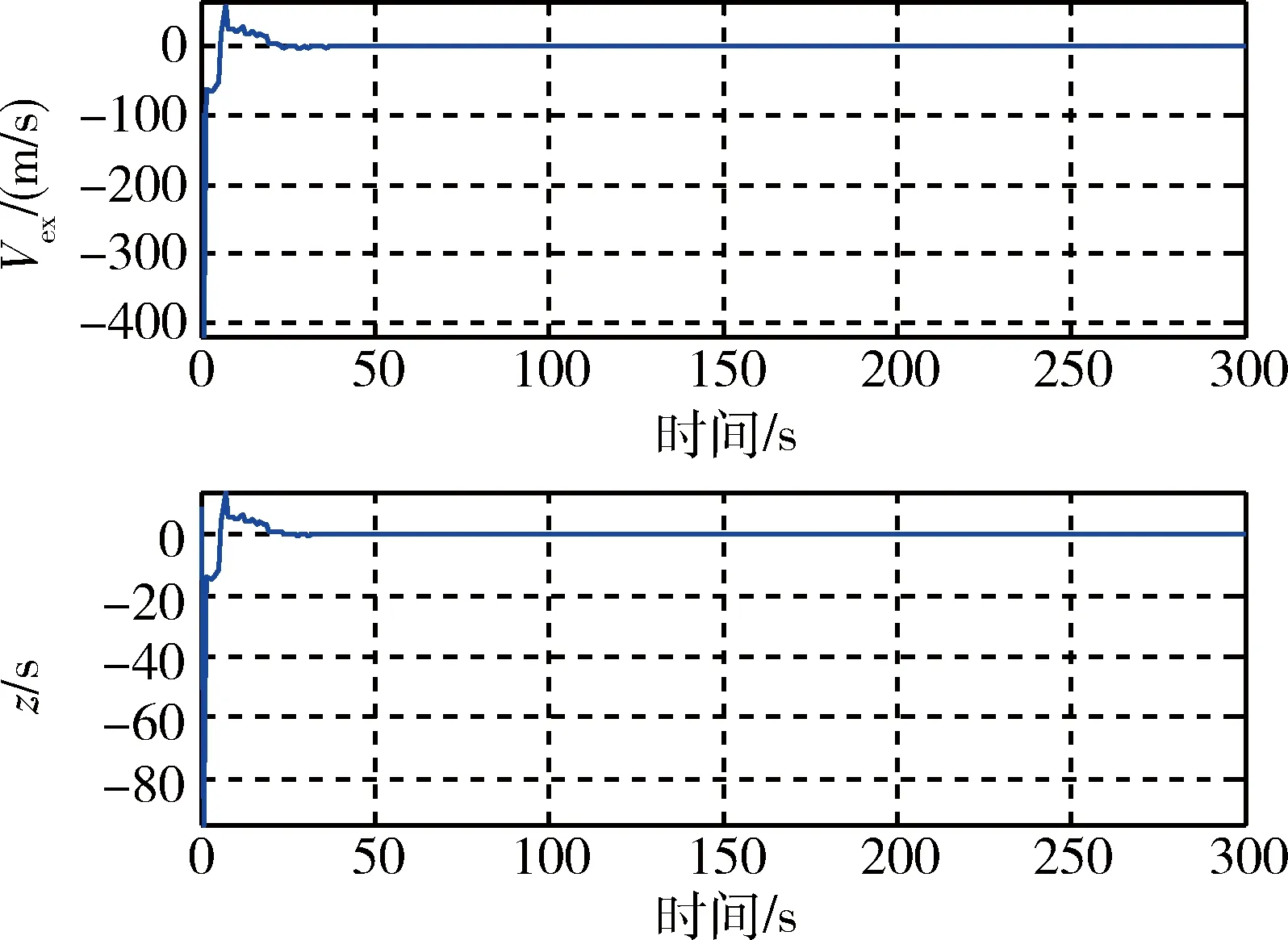
图2 参数估计偏差Fig.2 Estimation errors of parameters
未使用参数自适应估计的PEG仿真发现,终端时刻高度、速度大小、飞行路径角也满足要求,但其推力方向在接近制导末端时出现剧烈跳变,如图3~图4所示.从图4的局部图中可以看出,在这种情况下,虽然仿真时终端条件满足要求,但在实际中这其实是不可能实现的,因为制导末端推力方向剧烈变化,实际的姿控系统可能跟不上.为了避免终端推力剧烈变化,工程上采用制导末端一定时间内推力方向不更新的方法.但这种方法会导致终端制导精度变差.

图3 未进行参数估计时推力方向Fig.3 Thrustorientation without adaptive estimation

图4 未进行参数估计时推力方向(局部)Fig.4 Thrustorientation without adaptive estimation(zoom in)
通过对比仿真,可以看出进行参数自适应估计可以满足制导终端精度要求,同时终端推力变化平稳,不会出现跳变和振荡.
5 结 论
本文研究了PEG参数自适应问题.首先通过对PEG制导律的分析,将PEG中诸如质量、质量流量、比冲、推力等参数的自适应估计转化为对vex和τ的自适应估计.接着利用加速度计输出,使用卡尔曼滤波的方法得到参数的自适应估计.最后的对比仿真验证了PEG参数自适应估计的必要性和有效性.
[1] ROSE M B, GELLER D. Linear covariance techniques for powered ascent[C]//AIAA Guidance, Navigation, and Control Conference. Washiton D.C.:AIAA., 2010:1-21.
[2] 王志文,张洪华.基于线性协方差的月球上升器主动段误差分析[J].空间控制技术与应用,2014,40(3):25-30. WANG ZW, ZHANG HH. Error analysis based on linear covariance for lunar powered ascent phase[J]. Aerospace Control and Application, 2014,40(3):25-30.
[3] MCHENRY R., BRAND T J, LONG A D, et al, Space shuttle ascent guidance, navigation, and control[J]. Journal of Astronautical Sciences, 28(1):1979:1-38.
[4] SPRINGMANN P, PROULX R, Fill T. Lunar descent using sequential engine shutdown[C]//AIAA/AAS Astrodynamics Specialist Conference and Exhibit. Washiton D.C.AIAA:,2006:1-18.
[5] BRAND T J, BROWN D W; HIGGINS J P. Space shuttle GNC equation document NO.24 unified powered flight guidance[R]. Cambridge: Charles Stark Draper Laboratory, 1974:1-21.
[6] SEARS N E. Apollo guidance and navigation[R]. Cambridge: Instrumentation Laboratory,1979:495-497.
[7] ZARCHAN P, MUSOFF H. Fundamentals of Kalman filtering: a practical approach[M]. Reston, VA: American Institute of Aeronautics and Astronautics, 2000:129-182.
Adaptive Estimation of PEG Parameters During Lunar Ascent
WANG Zhiwen, ZHANG Honghua
(BeijingInstituteofControlEngineering,Beijing100190,China)
An adaptive parameter estimation method during PEG(powered explicit guidance) is proposed to solve the difference between true parameters of lunar ascent body and guidance parameters saved in guidance computer. Some parameters that have an influence on PEG are transferred to two parametersvexandτ, including mass, mass flow rate, specific impulse, force and so on. Based on accelerometer output, the parameters can be estimated. Finally the necessary and validity of the method are proved via comparing the PEG simulation results respectively with adaptive estimated parameters and the original parameters.
parameters; adaptive estimation; lunar powered ascent phase; PEG
2014-09-20
V44
A
1674-1579(2015)05-0028-05
10.3969/j.issn.1674-1579.2015.05.006
王志文(1988—),男,硕士研究生,研究方向为导航制导与控制;张洪华(1962—),男,研究员,博士生导师,研究方向为导航制导与控制,控制理论与控制工程.
