基于双目视觉的非合作目标逼近控制系统设计与仿真*
2015-06-09郭延宁郭增千马广富
郭延宁,韩 旭,郭增千,张 瑶,马广富
(1.哈尔滨工业大学控制科学与工程系,哈尔滨 150001; 2.上海卫星工程研究所,上海 200240)
基于双目视觉的非合作目标逼近控制系统设计与仿真*
郭延宁1,韩 旭2,郭增千1,张 瑶1,马广富1
(1.哈尔滨工业大学控制科学与工程系,哈尔滨 150001; 2.上海卫星工程研究所,上海 200240)
主要研究空间非合作目标近距离逼近过程的控制系统设计与仿真问题.针对采用双目视觉敏感器实现对非合作目标的观测情况,提出一种考虑成像误差的目标位置矢量计算方法,有效保证目标位置解算的可行性.在主星视线坐标系下,分别考虑逼近过程的最大相对速度约束、控制推力和力矩约束,设计了基于非线性项解耦的递阶饱和PID形式的近距离逼近位置控制律和姿态控制律,并在逼近过程中设置停泊点以确保与目标无碰撞.最后对典型航天器非合作目标抓捕任务进行了数学仿真,仿真结果表明所提出的方法可在满足各种约束的情况下有效实现任意方向的空间非合作目标的抓捕任务.
非合作目标;双目视觉敏感器;递阶饱和PID;位置控制;姿态控制;解耦控制.
0 引 言
空间非合作目标(non-cooperative target),是指并非设计用于对接或捕获任务的航天器或其他空间飞行物体,即该目标上不安装专门的抓持或对接机构以及用于辅助测量的合作标志器或特征块,不具备主动的姿态及轨道控制能力.其常泛指不能提供有效合作信息的空间目标,如未装置合作部件的卫星、燃料耗尽或发生故障的卫星、废旧弃用卫星、空间碎片,也可以是敌方卫星、敌方空间武器等[1-2].
空间非合作目标逼近过程的制导与控制系统的设计是实现抓捕或交会任务的最重要的任务之一,该问题一直受到国内外学者的重视.在相对导航的研究中,解永春等[3]提出了一种相对位置和相对速度导航方法,但其系统中采用单个敏感器,且需借助地面信息,主要工作于非合作目标远距离情况.张世杰等[4]提出了一种基于两次迭代计算的单目视觉相对位置姿态确定方法.徐文福等[5]系统地提出了基于立体视觉的空间机器人捕获非合作目标的测量与规划方法.已有研究多集中于对对象的识别与匹配,未考虑识别误差对导航计算方法的影响.
非合作目标的捕获任务最后逼近阶段指主星利用自身携带的光学载荷探测目标特性,逐渐近距离接近到达目标,然后利用机械臂或网爪等机构捕获目标的过程,该阶段是决定非合作目标抓捕任务成败的最关键的阶段[6].
已有用于合作目标交会对接任务的最终逼近段制导策略有R-bar、V-bar、基于C-W方程的反馈制导等[7-8].已有的方法在应对执行机构的控制能力、相对运动状态约束和与目标性的碰撞回避问题中均呈现诸多不足.双目视觉导航和和激光成像导航为最后逼近段的主要导航方法.
本文主要旨在解决采用双目视觉敏感器非合作目标逼近的两个问题:视觉敏感器存在测量误差情况的目标星矢量计算问题;考虑执行机构的控制约束、状态约束和碰撞约束的姿态及位置控制律设计问题.
1 敏感器建模及目标位置解算
1.1 双目视觉敏感器模型建立
双目视觉敏感器已经广泛应用于如机器人和各种飞行器的定位及导航中,工作原理图如图1.对于非合作目标捕获任务,不失一般性,认为双目视觉敏感器的基准坐标系Oxyz与主星本体坐标系三轴平行,其原点位于卫星本体系+x轴与外表面交点,其测量的相对距离信息即为卫星与目标之间的实际距离,可直接用于逼近控制阶段控制方案设计.
定义两个平行安装的敏感器焦点连线中心为基准坐标系原点O-xyz,视线方向定义为x轴,焦点连线方向定义为y轴(方向见图1),z轴构成右手坐标系,焦点距离为2a,两个敏感器的焦距均为f.视觉敏感器原点Ol在基准坐标系中的坐标为(f,-a,0),Or的坐标为(f,a,0).此外,为了描述单个敏感器观测范围,定义参考视场角θ如图1所示.
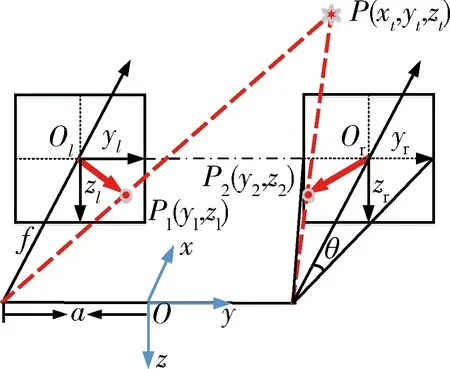
图1 双目视觉敏感器工作原理Fig.1 Structure of a binocular vision sensor
给定非合作目标中一特征点P(xt,yt,zt),不失一般性,认为该点为非合作目标且目标无高速自旋,在左、右敏感器的成像面上的像点分别为P1(0,y1,z1)和P2(0,y2,z2).由于这两个像点是空间中同一个对像点P在不同敏感器中的像,称为“共轭点”.当已知两个共轭像点和对应敏感器特性参数,分别作共轭像点与敏感器的焦点连线,在没有误差的情况下,就可以得到它们的交点,即为对像点P.
1.2 目标位置矢量解算
a)不考虑成像误差情况
在不考虑双目视觉敏感器的成像误差时,则根据透镜成像原理,有如下等式成立:
(1)
(2)
目标星的位置矢量的具体形式为:
(3)
b)考虑成像误差情况
考虑敏感器成像误差时,设左、右摄像机的误差矢量表示为(εy1,εz1)、(εy2,εz2),则有如下等式成立:
(4)
(5)
由于噪声的加入,使得左、右摄像机的共轭点与焦点连线不存在交点,进而无法得到目标位置,因此设计如下改进的位置计算策略.
根据三维空间的解析几何,有决定行列式
(6)
当Δ=2a(z1-z2)=0时,两视线相交,交点即为目标空间位置;当Δ=2a(z1-z2)≠0时,两视线异面,不存在空间交点,为使得视觉敏感器的误差折中抵消,不妨取两视线公垂线的中点为目标空间位置.
从而可知,观测的视线相交的充要条件为
z1=z2
(7)
当视线不相交时,有z1≠z2,两视线矢量为
(8)
可得两视线对应的直线方程分别为
(9)
则接下来的问题即为计算两条直线的公垂线和垂足,并将两个垂足的中点设为目标点即可,具体计算过程参见文献[9],此处不再赘述.
2 空间非合作目标逼近控制系统设计
2.1 系统总体设计
在对目标逼近过程中,利用主星配置的GPS和速率陀螺获取主星的绝对位置、速度和惯性角速度,由双目视觉敏感器解算目标的相对位置、相对速度等信息,并基于相对位置获取指向姿态,主星的轨道控制主要完成轨道机动及调整任务,不属于本文研究范畴;主星与目标的相对运动中,由主星位置控制器根据两星的相对位置及相对速度产生期望控制力指令,主星姿态控制器根据目标的视线角矢量和角速度信息提供控制力矩指令,再由推力器和反作用飞轮分别产生控制力和控制力矩作用至主星的轨道和姿态动力学模型中,最终完成空间非合作目标的逼近,系统结构如图2所示.
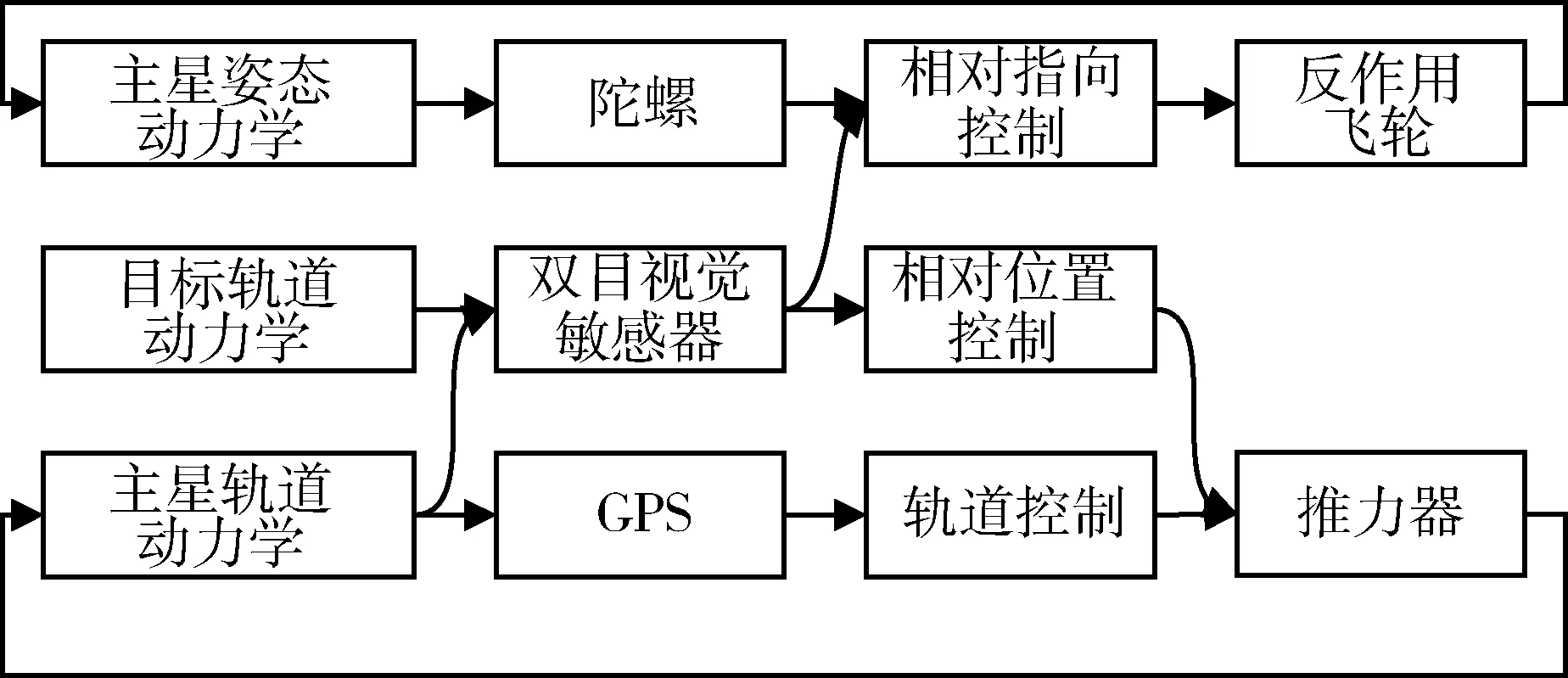
图2 空间非合作目标逼近控制系统结构Fig.2 Control system structure of non-cooperative target proximity operation
2.2 运动方程
选取地心惯性系为基准坐标系,则有考虑各种摄动力作用下的主星及目标轨道动力学方程为
(10)
(11)
式中,rs和rt分别为主星和目标在地心惯性坐标系下的三轴位置矢量,对应rs和rt分别为主星和目标地心距,μ为地球引力常数,fc为待设计的主星控制力,fsp和ftp为主星和目标的摄动集合.
不失一般性,考虑双目视觉与捕获系统安装在同一个方向,为满足以上需求,需要在视线坐标系下完成主星的控制系统设计.以主星本体系为参考系的视线坐标系,考虑忽略非合作目标和主星之间的万有引力作用,有视线坐标系的距离r、方位角α、高程角β计算如下:
(12)
对应分量表示的相对运动学方程为[8]
(13)
式中fi(i=r,α,β),Δgi(i=r,α,β)分别对应控制力和地心重力加速度差在不同运动维度的分量.对于最终逼近段而言,可以认为主星和目标所受重力加速度相同,即Δgi=0(i=r,α,β).
考虑飞轮作为执行机构,可得卫星本体系下的刚体姿态非线性动力学方程
(14)
式中,I为主星转动惯量矩阵,Tc为待设计控制力矩,Td为环境干扰力矩,ω×表示向量ω的反对称形式矩阵
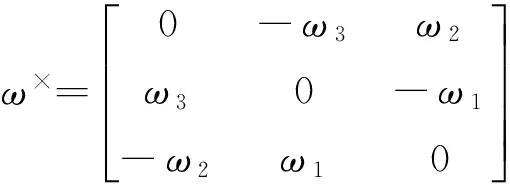
2.3 双积分系统的递阶饱和PID控制器
针对如下典型的控制受限情况下的双积分系统

(15)
其中,x为系统状态,u为控制量,k为常系数,对应U为控制量最大幅值.
对于给定期望状态xd,有时间最优控制[10]
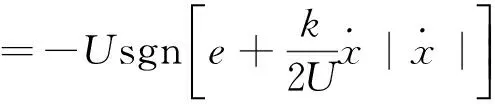
(16)
其中,e=x-xd,sgn为符号函数.
可以看出,由式(16)所示的最优控制在临界状态存在控制切换,进而带来抖动问题.因此,文献[11]提出了如下形式的PID递阶饱和控制器
(17)
其中,p、i、d分别为待选取得PID控制参数,饱和函数sat(·)定义为
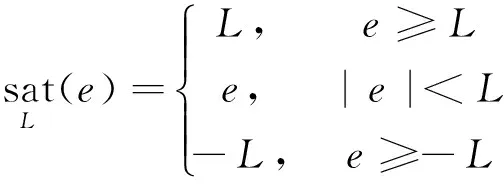
(18)
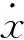
(19)
(20)
根据e的取值不同,最终对应两种可能的控制量,分别为
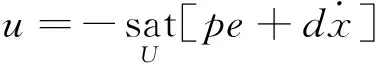
(21)
对应为普通饱和PD控制,以及
(22)
可等价对应得到时间最优控制(16).
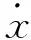
2.4 基于递阶饱和PID控制的逼近段位姿控制
在非合作目标的最后逼近段,主星需要完成以下任务:1)逼近过程始终保持目标星在主星视线范围内,或者使得视线方向与目标矢量方向重合,且两者无相对旋转;2)主星具备从任意方向逼近目标的能力,且逼近过程中两者不发生碰撞;3)主星和目标的相对距离和相对速度在一定时间内收敛到原点或指定状态;4)主星和目标的相对速度小于一定阈值,两者最终接近速度小于安全接近速度阈值.
要实现沿着任意方向逼近目标,可直接使得主星始终沿着视线方向逐渐逼近,因此可通过设计基于视线坐标系的控制策略完成位置和速度的控制,设计基于相对姿态的姿态控制策略完成指向控制.
对于位置控制而言,主星需要在视线轴方向上逐渐逼近目标,并使得视线在空间的转动角速度为零,不考虑导航误差和未建模特性,设运动过程中最大相对速度为vmax,最大控制推力为Fmax,则有基于非线性解耦的递阶饱和PID位置控制器为
(23)
式中,m为主星质量,pr、ir、dr、dα、dβ为待定参数,且
将控制器(23)代入运动学方程(13),有
(24)
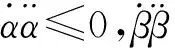
根据定义,有视线坐标系到本体坐标系的转换矩阵如下所示:
(25)
则有主星本体系下的控制力指令矢量为
(26)
对于相对姿态控制,则需要满足主星逼近过程始终指向目标,需将方位角和高程角均调节到零,且在视线轴方向无相对旋转运动,有三轴本体系对应的控制力矩分量分别为:
(27)
其中,ωx为视线轴惯性角速度,dtx,pty等均为待定控制参数,Tmax为各轴最大力矩.
2.5 停泊点设置
为保证在近距离交会过程中不发生碰撞损失,并增强任务的灵活性,在对目标星抓捕之前可增加一些特定的控制目标,即设置停泊点.在停泊点处可以实现抓捕设备的校准、故障排查以及指令等待,通过停泊点的设置可以增强最终逼近段的时间调整能力.
3 仿真系统建立与分析
为验证本文设计系统的有效性,利用Matlab/Simulink,构建了可模拟非合作目标逼近过程的仿真系统.
不失一般性,认为主星和目标处于同一轨道的不同位置,对应轨道半长轴7 000 km,偏心率0,轨道倾角97°,近地点幅角30°,升交点赤经70°,主星和目标的平近点角分别为25°和25.000 2°,对应的地心惯性坐标系的初始速度和位置参数以及系统参数如表1所示.
设初始条件下目标位于主星视线轴方向,对应目标在主星本体系相对位置矢量为[24.43 0 0] m.不考虑双目视觉敏感器视场约束和轨道摄动加速度以及干扰力矩作用,利用基于本文设计的算法构建的仿真系统,针对上述系统进行数学仿真,可得结果如图3~7所示.
由图3可以明显看出,在考虑双目视觉敏感器一定测量误差的情况下,主星依次完成了对两个停泊点的逼近和悬停任务,且始终没有与目标发生碰撞,且停泊点2可以根据主星抓捕系统配置选取,以实现安全高效逼近;图4给出的相对速度表明本文设计的位置控制器可满足对最大相对速度的约束,且以近似时间最优控制的特性依次完成不同停泊点逼近任务,其中前50 s的速度抖动主要由于初始速度误差和姿态控制的叠加作用引起;图5为主星控制推力矢量变化曲线,可以看出推力器近似呈现“bang-off-bang”的工作模式,有效发挥推力器最大控制能力,并在到达停泊点附近后切换为连续控制,避免系统振动;图6给出了目标相对主星的方位角和高程角变化曲线,可以看出两个角度在整个逼近过程始终保持在极小的范围内,说明了姿态控制的有效性,需要说明的是出于任务需求和能量节约的综合考虑,此处姿态控制的积分参数设置为0,且在目标和主星相对距离小于0.5 m时即停止姿态控制(对应约220~290 s和340~500 s),对应的控制力矩变化曲线如图7所示.

表1 卫星及控制器仿真参数表
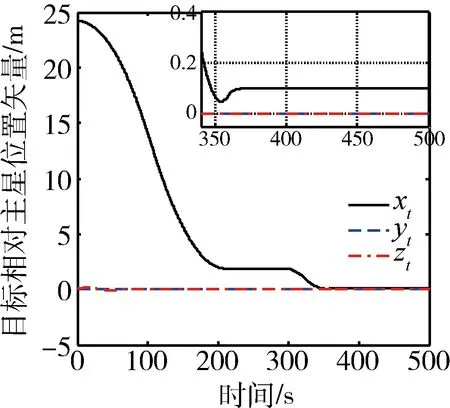
图3 相对位置变化曲线(主星本体坐标系)Fig.3 Time history of relative position in spacecraft body frame
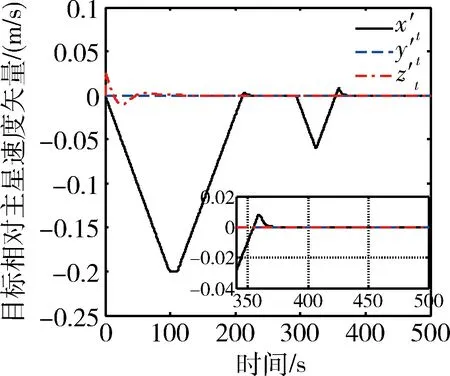
图4 相对速度变化曲线(主星本体坐标系)Fig.4 Time history of relative velocity in spacecraft body frame
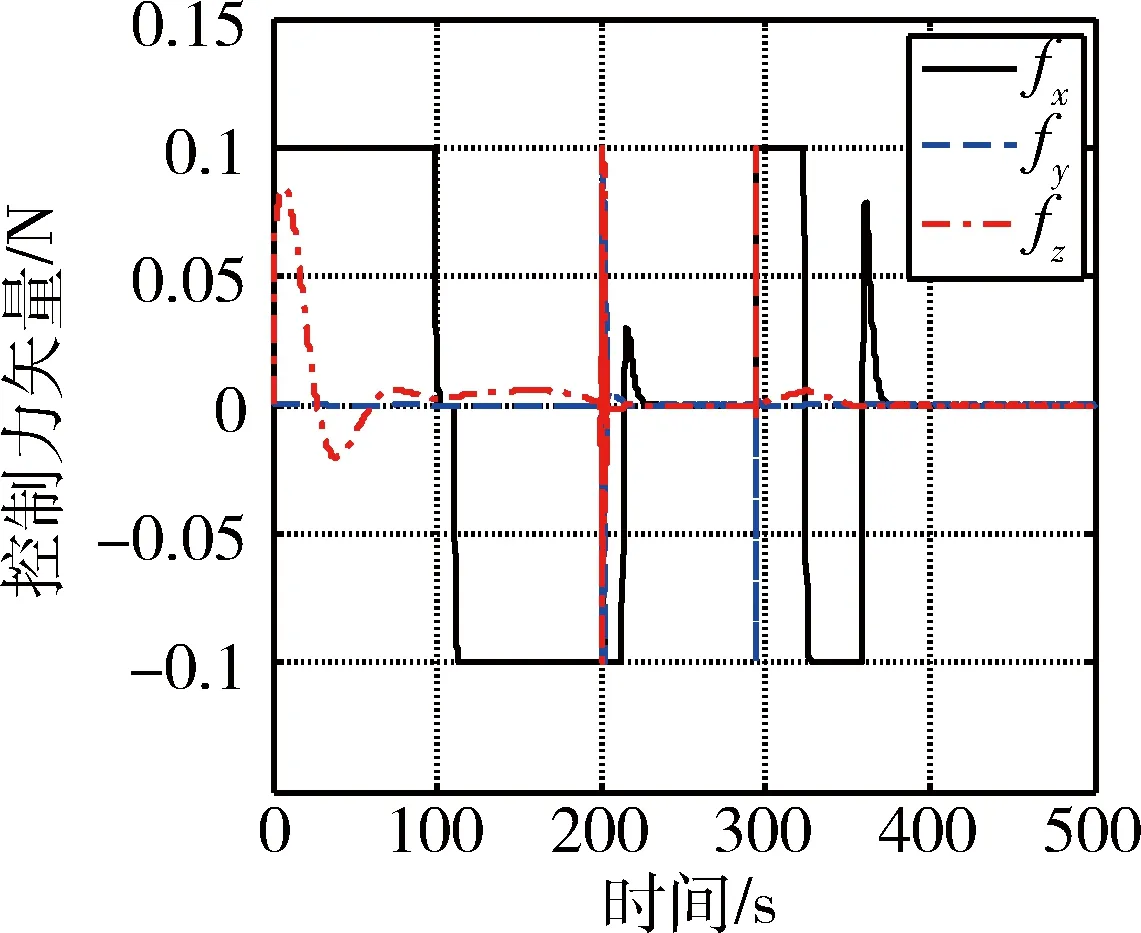
图5 控制推力变化曲线(主星本体坐标系)Fig.5 Time history of control force in spacecraft body frame
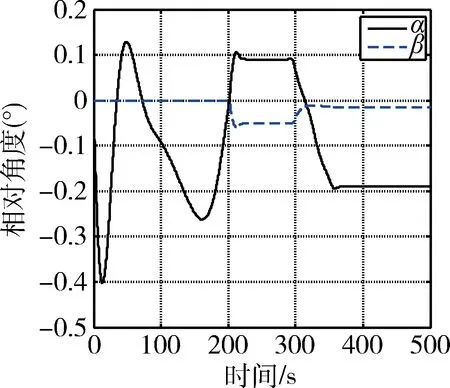
图6 目标指向角度变化曲线(主星视线坐标系)Fig.6 Time history of pointing angles of target in spacecraft line-of-sight frame
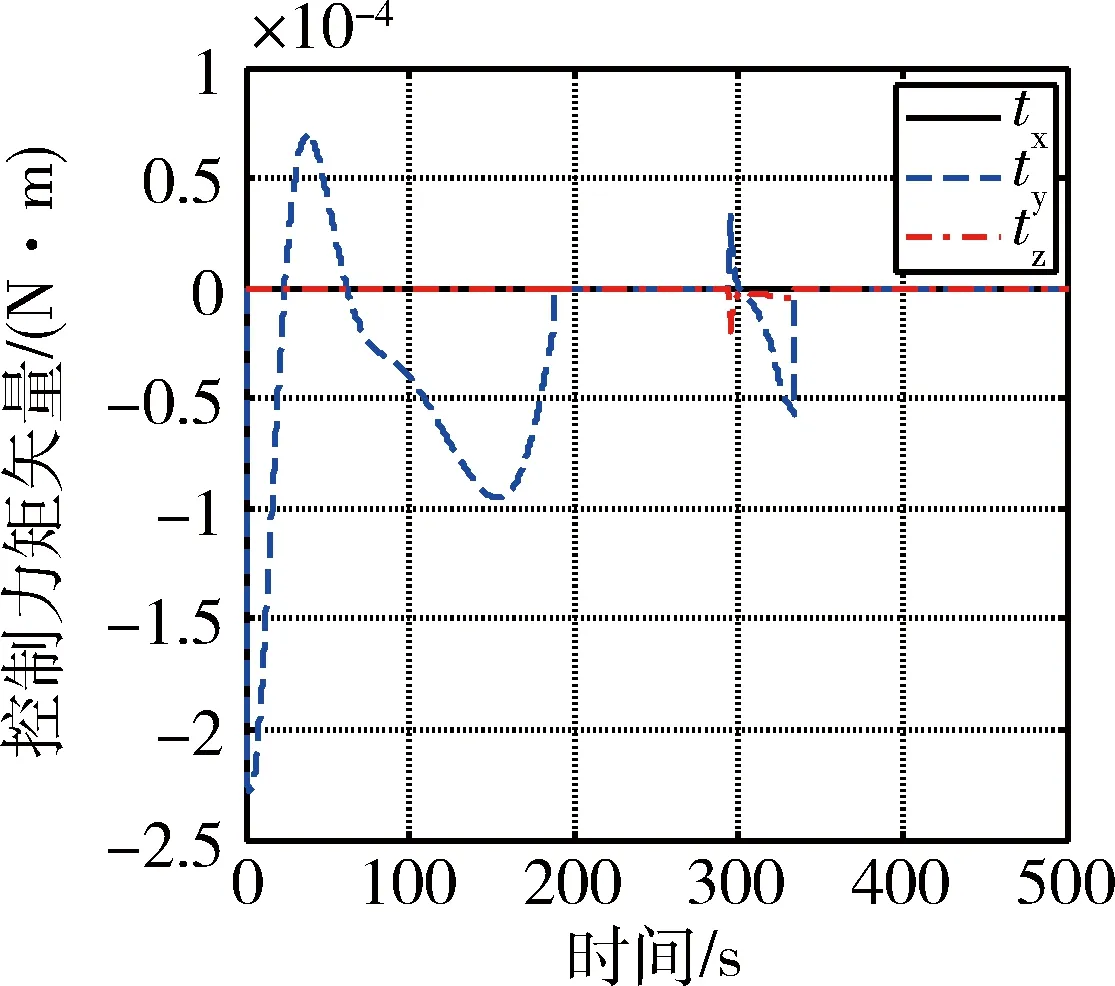
图7 控制力矩变化曲线(主星本体坐标系)Fig.7 Time history of control torque in spacecraft body frame
4 结 论
本文设计了一种带有成像误差的双目视觉敏感器目标位置矢量解算方法,用于非合作目标的最后逼近任务.考虑系统的快速性、能量消耗、可靠性需求以及速度约束和控制约束等,设计具有时间最优特性的递阶饱和PID位置控制律和姿态控制律.通过构建一个包含轨道及姿态动力学模型、敏感器测量模型、执行机构动力学模型以及控制律模块的综合仿真系统,对本文提出的方法进行验证.数学仿真结果表明,设计的控制方案可依次完成停泊点的逼近任务,结合停泊点的设计可完成任意方向的目标逼近任务,且整个飞行过程未与目标发生碰撞,充分说明了设计算法的有效性和优越性.
此外,设计过程并未考虑推力器具体配置,即考虑主星可在任意方向产生推力而无需姿态机动,并且在实际的非合作和合作目标的近距离逼近过程中,姿态和轨道的耦合动力学是需要重点考虑的重要内容,在未来研究中可针对特定推力器配置开展控制分配优化和考虑推力配置约束的位姿控制方案设计.
[1] 李金宗, 逯仁贵等. 空间交会对接技术[M]. 哈尔滨工业大学出版社,1997.
[2] 唐国金, 罗亚中等. 空间交会对接任务规划[M]. 科学出版社,2008.
[3] 刘涛,解永春. 非合作目标交会相对导航方法研究[J]. 航天控制,2006,24(2):48-53. LIU T, XIE Y C. A Study on relative navigation for spacecraft rendezvous with a non-cooperative target[J]. Aerospace Control, 2006,24(2):48-53.
[4] 张世杰,曹喜滨,张凡. 基于特征点的空间目标三维位姿单目视觉确定算法[J]. 中国科学:信息科学, 2010,40(4):591-604.
[5] 徐文福,梁斌,李成.空间机器人捕获非合作目标的测量与规划方法[J]. 机器人, 2010,32(1):61-69. XU W F, LIANG B, LI C. Measurement and planning approach of space robot for capturing non-cooperative target[J]. Robot, 2010,32(1):61-69.
[6] 陈小平.航天器自主交会对接导航与控制关键技术研究[D]. 电子科技大学博士学位论文, 2012. CHENG X P. Key techniques of navigation and control for autonomous rendezvous and docking of spacecraft[D]. Chengdu: University of Electronic Science and Technology of China, 2012.
[7] 张柏楠. 航天器交会对接任务分析与设计[M]. 北京:科学出版社,2011.
[8] 张立佳. 空间非合作目标飞行器在轨交会控制研究[D]. 哈尔滨工业大学博士学位论文, 2008. ZHANG L J. Research on control for rendezvous with noncooperative target in orbit[D]. Harbin: Harbin Institute of Technology, 2008.
[9] 董玉久,潘秀英,杨欣欣. 两异面直线公垂线垂足位置的计算方法[J]. 哈尔滨科学技术大学学报, 1990,14(1):84-88. DONG Y J, PAN X Y, YANG X X. A calculation method for finding the foot of common perpendciular of lines on different places[J]. Journal of Harbin University of Science and Technology, 1990,14(1):84-88.
[10] 李传江, 马广富. 最优控制[M]. 北京:科学出版社, 2011.
[11] WIE B, LU J. Feedback control logic for spacecraft eigenaxis rotations under slew rate and control constraints [J]. Journal of Guidance, Control, and Dynamics, 1995,18(6):1372-1379.
Control System Design and Simulation of Binocular Vision-Based Non-Cooperative Target Proximity Mission
GUO Yanning1, HAN Xu2, GUO Zengqian1, ZHANG Yao1, MA Guangfu1
(1.HarbinInstituteofTechnology,Dept.ofcontrolscienceandengineering,Harbin150001,China;2.ShanghaiInstituteofSatelliteEngineering,Shanghai200240,China)
The control system design and simulation of non-cooperative target proximity mission are investigated. Considering binocular vision sensor with imaging errors, a new relative position computation method is proposed to obtain the position of non-cooperative target. With constraints like maximum relative velocity, control force and control torque, the cascade saturation PID control based on nonlinear decoupled position control and attitude control algorithms are developed in the line-of-sight coordinate system. Further, holding points are adopted in conjunction with the proposed control methods to avoid collision with the target. Numerical simulation results in a typical non-cooperative target proximity scenario are provided to demonstrate the effectiveness and reliability of the proposed strategy.
non-cooperative target; binocular vision sensor; cascade saturation PID; position control; attitude control; decoupling control
*国家自然科学基金资助项目(61403103),中国博士后科学基金资助项目(2014M550195)和中央高校基本科研业务费专项资金资助项目(HIT.NSRIF. 2013135,HIT.NSRIF.2014035).
2015-03-03
V412.4
A
1674-1579(2015)05-0006-06
10.3969/j.issn.1674-1579.2015.05.002
郭延宁(1985—),男,博士,讲师,研究方向为航天器姿态动力学与控制,深空探测制导与控制技术等;韩 旭(1982—),男,高级工程师,研究方向为航天器系统试计与测试,航天器动力学与控制;郭增千(1994—),男,本科,研究方向为航天器控制系统设计;张 瑶(1989—),女,博士研究生,研究方向为航天器制导系统设计、非线性控制等;马广富(1963—),男,教授,研究方向为最优控制、航天器动力学与控制,非合作目标近距离操作等.
