基于Maple环境的测量不确定度评估方法

邱国平

(广东省印刷技术研究所，广州 510650)



基于Maple环境的测量不确定度评估方法

邱国平

(广东省印刷技术研究所，广州 510650)

评定测量不确定度，通常的计算方法是GUM，MCM作为GUM的补充。本文通过Maple软件用解析方法与改进的MCM成功解决大部分测量不确定度的精确评估，同时通过解析方法可以判断其他方法的精确度。最后，揭示使用Maple软件的解析方法的某些局限。

测量不确定度；Maple；GUM；MCM；概率密度函数

0 引言

测量不确定度的定义：简称不确定度，根据所用到的信息，表征赋予被测量值分散性的非负参数[1]。测量不确定度评定与表示已成为国际科技交流与贸易中一项重要的指标。《校准和检测实验室能力的通用要求》(ISO/IEC 17025)中明确要求：实验室的每个证书或报告，必须包含有关校准与测试结果不确定度评定的说明。《测量不确定度评定与表示》从原来的JJF 1059—1999到现在的JJF 1059.1/2—2012，从单一的GUM到MCM的诞生。测量不确定度评定得到进一步的深化，方法得以扩展。

可以有效采用GUM评定测量不确定度的要求[2]：1)数学模型的非线性不是很明显；2)中心极限定理适用，这意味着输出量的PDF是由高斯分布或t分布表示；3)韦尔奇-萨特斯韦特公式足够用来计算有效自由度。应用韦尔奇-萨特斯韦特公式要求假定输入量相互独立。在许多情况下，上面的条件是接近符合的，所以在实际应用中是完全可以接受的。这也是GUM应用最广泛的原因。但在某些情况下，却未必如此。MCM是一种数值计算方法，MCM的引入大大拓宽可以评定测量不确定度的范围。MCM的局限：1)如果输入量分布广，输出量的分布集中，仿真的结果不稳定，不能很好收敛。下文的例子可以说明这一点；2)MCM计算的精度有限。对于可以收敛的测量不确定评定，如果希望得到更精确的数值，需要提高仿真的数据量。这对计算机或软件的要求将大大提升。本文利用Maple的统计工具包，使用解析方法一定程度上解决以上两个问题。同时通过解析方法可以判断其他方法的精确度。最后指出解析方法的一些不足之处。解析方法与MCM都可以作为GUM的有力补充。

1 测量不确定度评定

对于单个随机变量而且不需要函数转换的，我们可以通过经验判断随机变量的概率分布函数或者用贝塞尔公式对其测量不确定度评定。但是实际中输入量与输出量有较为复杂的模型。N个输入量，记为X=(X1,…,XN)T和输出量Y之间的关系可用如下模型表示：Y=f(X)=f(X1,…,XN)。测量不确定度由X中的N个输入量的分布以及模型决定。GUM一般使用一阶泰勒级数近似的不确定度传播律评定测量不确定度。如果模型是线性的，输入量为高斯分布，而且明确输入量之间的相关性。这种情况下，GUM是无与伦比的。对于非线性的数学模型，GUM使用高阶泰勒级数展开的方法扩展了GUM的可评定测量不确定度的范围，但是泰勒级数近似计算操作性不强[2]。使用解析方法是最准确的方法，解析方法被认为是困难的方法。在Maple软件环境下，很多现实中的问题可以得到结果。过于复杂的模型，通过精确计算某些特征量可以判断其他方法的精确度。MCM[2]考虑了输入量的概率密度函数(PDF)，就是输入量的分布。MCM提供丰富的信息，通过测量模型Y=f(X)=f(X1,…,XN)传播输入量X的PDF(而不是这些量的估计值的测量不确定度)以获得输出量Y的PDF。从输出量Y的PDF，可以直接获取包含区间以及其他的统计信息。

2 Maple的统计工具包简介

Maple软件是“枫叶之国”加拿大的滑铁卢大学开发的数学符号计算软件。在Maple、Mathematica、Matlab以及Mathcad四大数学软件中以符号计算见长。Maple提供众多的函数、命令。统计工具包使用最先进的符号计算法，为概率数理统计等统计方面提供140多个函数，为Maple在处理统计方面的问题提供强大的支持。使用Maple的统计工具包处理测量不确定度问题，我们可以看出Maple软件的强大功能。

3 Maple在测量不确定度评定中的应用

3.1 不同均匀合成[3]

由上面的结果我们知道Maple提供更加准确的结果，得到的包含区间是[-17.02,17.02]。准确的数值Maple也可以计算出来。上面我们发现包含区间端值互为相反数，是否隐含Y的PDF为对称函数？同样可以使用强大的Maple软件得到Y的准确PDF(gY(x))如下：

从上面的函数我们可以看出Y的PDF的对称性。

3.2 简单的指数模型

Y=7X,X∝N(0,1)。这种模型是不适合使用GUM的，Y的期望值也出现错误。使用MCM计算，我们发现Y的标准差出现波动，Y的期望值还是能够比较好收敛的。如下现实中的两次的MCM模拟值(95%置信概率的包含区间用2.5%、97.5%代表的分位数表示)：1)均值、标准偏差以及包含区间分别为：6.62、41.02、[0.02，45.27]；2)6.61、36.79，[0.02，45.36]。下面用Maple将Y的均值、标准偏差以及包含区间精确计算出来(Maple程序略)。

由此，我们得到Y的精确的均值、标准偏差以及包含区间为6.64、43.60与[0.0245.33]。从上例我们发现：对于极端集中分布的Y，虽然MCM不能很好模拟标准偏差，但是对于均值以及包含区间的模拟却能达到比较好的结果。但是，对于形如Y=Xn(n>0),X∝N(0,1)或Y=aX(a>0),X∝N(0,1)的模型，如果n或a的数值比较大时，MCM模拟的均值以及标准偏差都会偏离。这可能是此广义积分不存在的缘故。

3.3 均匀分布与反正弦分布的合成[4-7]

Y=X1+X2;X1∝U[-a,a],X2∝As[-e,e],a>0,e>0。X1,X2独立。文献[5]通过复杂的运算将Y的概率密度函数、图形以及包含因子计算出来。这里用Maple可以实现上面的所有功能。我们发现文献[5]的包含因子可以修正(Maple程序略)。

包含因子为1.87(95%的置信概率)，与文献[5]的结果吻合。文献[5]使用大量的时间在此，因为包含因子的计算本质上是一个解方程问题。通过改变a与e的值，同时改变置信概率我们得到一系列的数值以制成通用的表格。对于与文献[4]，我们同样可以采用此方法计算得出。应用统计工具包的PDF函数，我们可以计算得出Y的概率密度函数，从而作出他们的图像。如图1所示。

3.4 质量校准[2，7]

质量校准的数学模型：

100000

mR,C∝N(100000,0.050);δmR,C∝N(1.234,0.020);ρa∝U[1.10,1.30];ρW∝U[7000,9000];ρR∝U[7950,8050].各自变量相互独立。

此模型过于复杂，Maple软件也不能使用符号计算得到测量不确定度。但是Maple计算Y的均值与标准偏差是可行的。通过精确计算Y的均值与标准偏差来给MCM计算的数值提供一定的参考。Maple可以使用Sample命令实现数值模拟。同时我们可以发现Maple数值模拟与一般软件的不同之处在于其可以直接通过模型仿真数据，这样可以减少储存空间。对于比较多的自变量更能体现其优点(Maple程序略)。

由以上的结果我们可以发现精确的均值与标准偏差为1.23400与0.075480；仿真计算得到的均值与标准偏差为1.23399与0.075486。这样我们可以比较肯定地说明仿真的结果可以接受。最后我们得到Y的95%置信概率的包含区间为[1.0843，1.3836]，区间较[1.0834，1.3825][8]略宽。同样可以使用Maple的Histogram命令作出Y的概率密度图像(图2)。

4 结束语

本文通过Maple软件用解析方法与改进的MCM

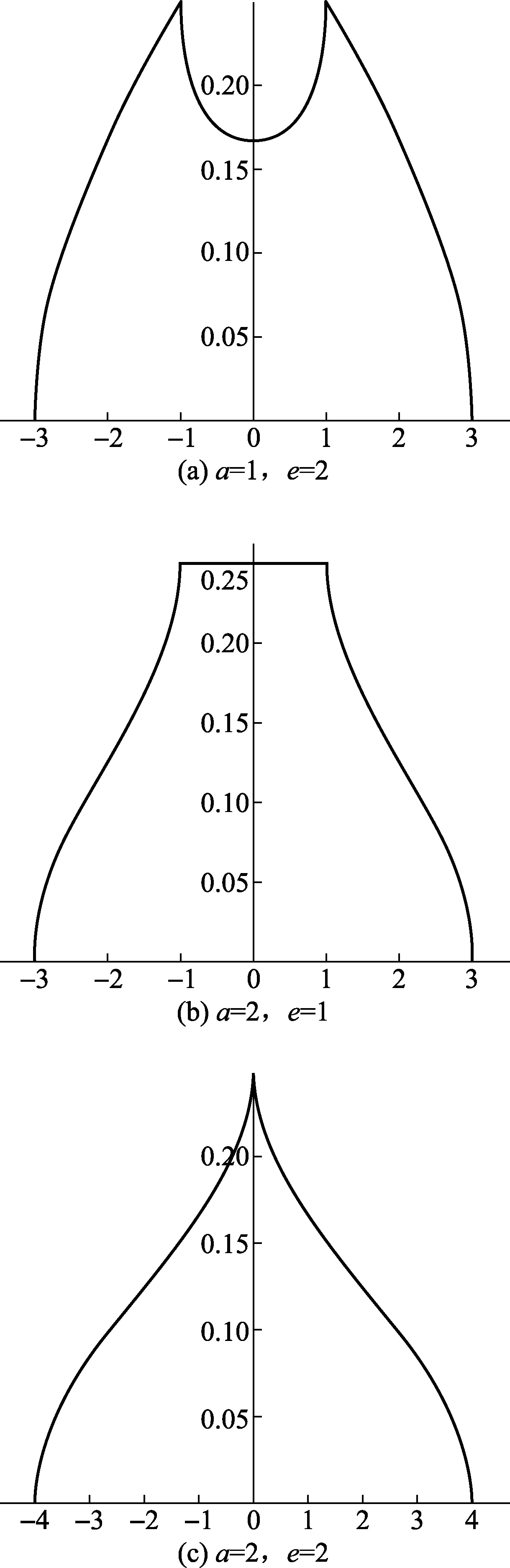
图1 均匀分布与反正弦分布的合成分布密度

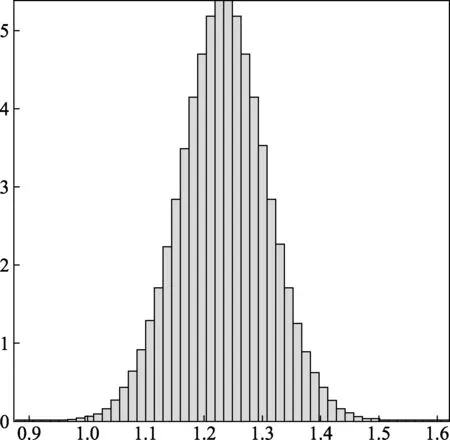
图2 Y的分布密度

成功解决大部分测量不确定度的精确评估，同时通过解析方法可以判断其他方法的精确度。对于异常复杂的数学模型，Maple也可以应用蒙特卡洛法评估测量不确定度。而且Maple的命令更为简洁、精确。Maple能够定制不同的分布、处理离散的分布。对于某些特定的分布合成，通过Maple可以制成有关包含因子的表格。这样对GUM的运用有很大的实用意义。使用解析方法，包含区间的获取可以看作一个复杂方程的求解问题，Maple能够很好胜任。Maple的解析方法的最大缺陷是不能处理有关相关变量的测量不确定度问题。当然，这问题可以使用蒙特卡洛法模拟仿真。使用Maple提供的解析方法以及改进的MCM为评定测量不确定度评估提供可行的路径，可作为GUM的有力补充。

[1] JJF 1059.1—2012测量不确定度评定与表示[S].北京：中国质检出版社

[2] 周庚桃.用蒙特卡洛法评定测量不确定度[M].北京：中国质检出版社，2013

[3] 刘智敏.用MC仿真计算不确定度[J].中国计量学院学报，2005，16(1)：1-7

[4] 刘智敏.不确定度与分布合成[J].物理实验，1998，19(5)：17-19

[5] 林世曾.均匀分布与反正弦分布的误差合成[J].计量技术，1996(5)：36-39

[6] 刘智敏.实验室认可中的不确定度和统计分析[M].北京：中国标准出版社，2007

[7] 甘晓川，周鑫，赫明钊，叶孝佑.一种不确定度的卷积评定方法[J].计量技术，2012(4)：3-6

[8] JJF 1059.2—2012用蒙特卡洛法评定测量不确定度[S].北京：中国质检出版社

10.3969/j.issn.1000-0771.2015.3.21