铝镍钴永磁体磁参量的测量不确定度评估*

许志一 李小菊 龚文杰 贺 建 侯瑞芬 张志高 范 雯 林安利

(中国计量科学研究院，北京 100029)



铝镍钴永磁体磁参量的测量不确定度评估*

许志一 李小菊 龚文杰 贺 建 侯瑞芬 张志高 范 雯 林安利

(中国计量科学研究院，北京 100029)

在中国计量科学研究院的硬磁材料磁特性检定装置上进行铝镍钴标样测试试验，分析了铝镍钴磁参量的测量不确定来源，通过独立重复试验数据的统计和数学模型的建立，评估了剩磁、矫顽力、内秉矫顽力和最大磁能积的扩展不确定度。

铝镍钴；磁测量；不确定度

0 引言

铝镍钴(以下以Alnico表示)是较早开发出来的一种永磁材料，其优点是剩磁高、温度系数小、使用温度高，广泛应用于永磁电机、仪器仪表等。Alnico永磁材料使用性能的好坏直接与其磁参量有关[1]，主要包括：剩磁Br、内禀矫顽力HcJ、矫顽力HcB和最大磁能积(BH)max。永磁材料生产企业和测试计量机构都需要对这四个参量进行测量，以判别其质量优劣，为用户选材及研究者作研发提供技术数据支撑。国际上，普遍以IEC 60404-5作为永磁材料的测量标准[2]，我国紧跟国际形势，于2013年对永磁材料测量标准进行了修订，并发布了新版本国标[3]，为国内的永磁材料磁性测量提供权威技术规范。王子生等[4]为Alnico的磁参量测量建立了不确定度数学模型并作出了详细分析，本文在硬磁材料磁特性检定装置MTP-500H上进行了Alnico标准样品的测量，对所得磁参量开展了测量不确定度评估研究。

1 试验依据和方法

按照GB/T 3217—2013规定[3]，对于HcJ≤600kA/m的永磁材料例如Alnico、铁氧体等，一般用B线圈来测量磁通密度，用基于Hall效应的高斯计或特斯拉计测量磁场强度，而磁通量Φ由磁通计测量得到。不同测试人员使用中国计量科学研究院的硬磁材料磁特性检定装置(MTP-500H)，对Alnico圆柱标样NIM0106(高度为19.06mm)进行10次独立测量；用表面温度计测得样品的温度为19.8℃。结合技术规范JJF 1059.1—2012[5]及文献[6,7]评估了测量结果的不确定度。

2 磁参量的测量不确定度评估

Alnico永磁体磁参量(剩磁Br、内禀矫顽力HcJ、矫顽力HcB和最大磁能积(BH)max)的测量不确定来源主要包括：测量装置产生的，测量时偏离正常工作条件产生的，测量重复性导致的。

2.1 剩磁Br的不确定度分析

磁通密度B的计算式为：

B=Φ/(NS)

式中，Φ是磁通计测得的磁通量；N是B线圈的匝数；S是线圈包围部分试样的截面积。由于B线圈探测到的信号中包含空气磁通，应予以修正，修正后的磁通密度为：

B=Φ/(NS)-μ0H(St-S)/S

式中，H是与磁通密度B对应的磁场强度；St是测量线圈的有效横截面积；μ0为真空磁导率。

测量过程中，B线圈采用线径为小于0.15mm的漆包线单层、均匀且紧密地缠绕于试样中部，经修正后空气磁通引入的不确定度忽略不计。B线圈匝数N是一整常数，其不确定度视为零。

2.1.1 剩磁Br的测量模型

2.1.2 测量装置产生的不确定度

2.1.2.1 样品直径测量的影响δD

因此，直径测量引入的标准不确定度为：

=[(0.0012)2+(0.001)2]1/2

≈0.0016mm

相对不确定度为：

=(0.0016/16.501)×100%

≈0.0097%

2.1.2.2 磁通计测量磁通的影响δΦ

根据磁通计的检定证书，扩展不确定度U=0.2%，k=3，其相对不确定度为：

urel(Φ)=u(Φ)/Φ=U/k=0.2%/3≈0.067%

在校准过程中，磁通量程通常选择在1/2满量程以上，磁通Φ的相对不确定度为：

urel(δΦ)=2urel(Φ)=0.067%×2=0.134%

对圆柱标样，其截面积为：S=pD2/4，因此，由测量装置产生的相对不确定度为：

urel(δBr1) =[urel2(δΦ)+(-2)2×urel2(δD)]1/2

=[(0.134%)2+(-2×

0.0097%)2]1/2

≈0.135%

2.1.3 测量时偏离正常工作条件引起的不确定度

1)磁通计分辨力对测量结果的影响δf：采用了14位A/D和D/A，其分辨力为0.01%。如果B通道磁通计的量程选用5μWb，则每一个读数值可能误差应在±0.00025μWb范围内。假定在该范围内满足矩形分布，于是所引入的不确定度分量为：

2)磁场均匀区的影响δS：从电磁铁的校准报告可知，在以电磁铁极头中心为原点，直径为20mm的区域内，磁场不均匀性不超过0.019%。校准时规定试样的最大直径为18mm，并对样品进行多次测量，取其平均值，因此，可以认为磁场不均匀性所带来的影响urel(δS)小于0.019%。

3)磁通计的漂移影响δp：由A/D对积分器输出进行实时采样，测量出积分器在固定时间间隔内的变化，再由单片机计算出合适的D/A值，然后反馈到运算放大器的输入端，补偿引起漂移的偏置电压。通过实验，将磁通计调至稳定后开始计时，3min内记录磁通计的漂移值，其变化量均在0.01%以内。如果将整个测量时间控制在3min以内，并对测量结果进行漂移修正，磁通计漂移对测量结果的影响urel(δp)可小于0.010%。

4)温度变化对Br的影响δΔT：Alnico永磁的剩磁温度系数很小(取a =0.002%/℃)，在实际测量时采用表面温度计直接测量样品温度，认为给出的是样品的实际温度，因此温度变化带来的不确定度非常小，可以忽略(即aΔT≈0)，认为urel(δΔT)=0。

6)样品端面与极面之间气隙的影响δg：气隙的影响可表达为：ΔH/H=-(2gB)/(μ0LH)，其中，B、H为退磁曲线上给定点的磁通密度和磁场强度；L为试样长度；g为试样和极面间的气隙。

测试时对试样要作出严格要求，即试样内部及外部不能有砂眼、缺口、裂纹或其他缺陷，端面应相互平行，其平行度不超过公差等级9级，端面垂直于轴线，垂直度不超过公差等级9级，表面粗糙度Ra≤1.6μm。最大气隙可视为g=1.6μm，样品两端面的总气隙为2×1.6μm=3.2μm。对于高度为19.06mm的标准样品，气隙带来的相对不确定度urel(δg)=(3.2μm/19.06mm)×100%=0.017%。

综合上述可得偏离规定的正常工作条件所引起的相对不确定度为：

urel(δBr2) =[urel2(δS)+[urel2(δp)+urel2(δg)]1/2

=[(0.019%)2+(0.010%)2+

(0.017%)2]1/2=0.027%

2.1.4 测量重复性所产生的不确定度

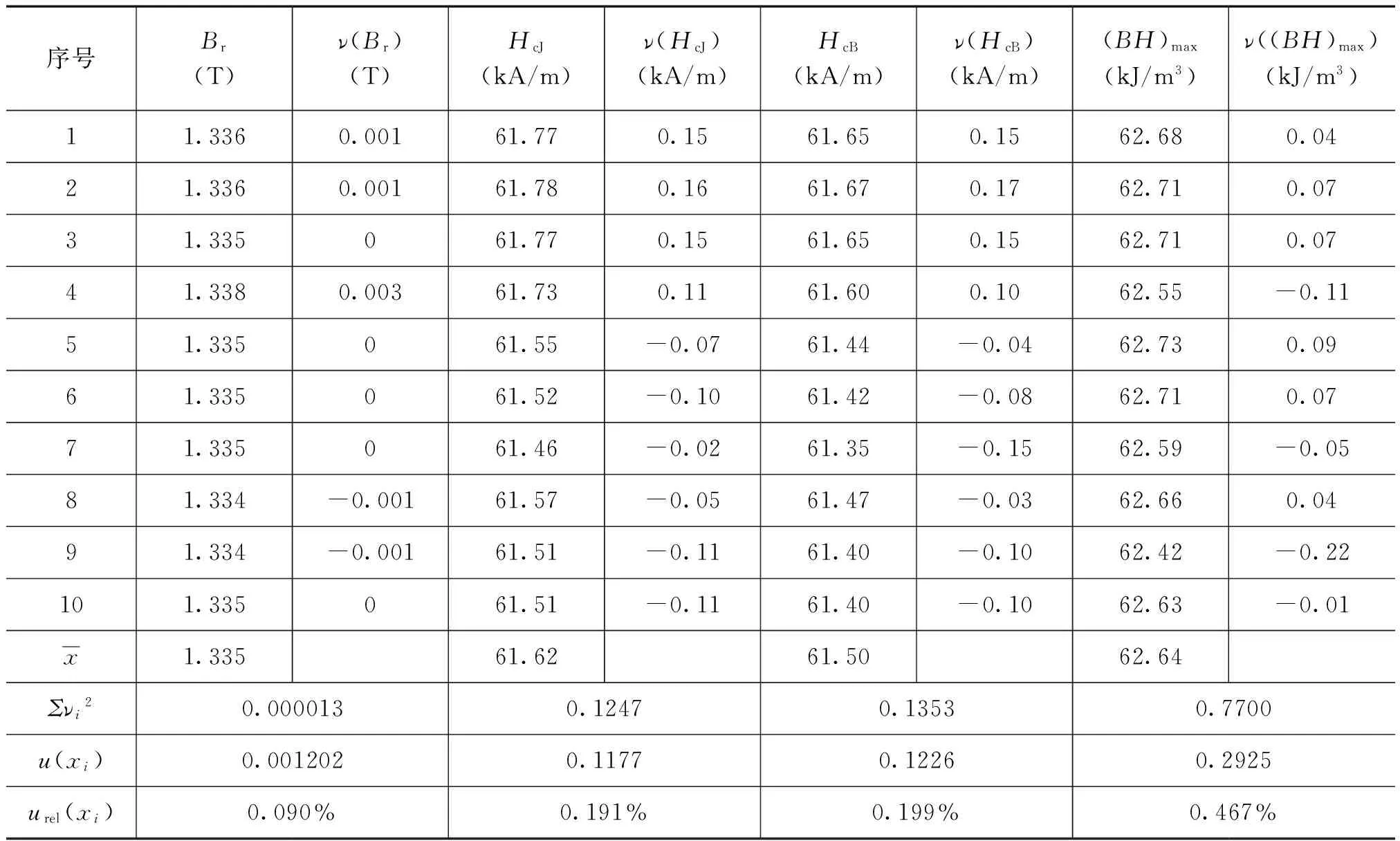
表1 Alnico标样的10次测量结果

2.1.5 剩磁Br的扩展不确定度计算

=[(0.090%)2+(0.135%)2+

(0.027%)2]1/2≈0.16%

取置信概率p=95%，k=2，则剩磁Br的扩展不确定度为：Urel(Br)=k×urel(Br)=2×0.16%=0.32%。

2.2 矫顽力HcB和HcJ的不确定度分析

2.2.1 矫顽力HcB的测量模型

其中，β为温度系数；ΔT为样品温度与测量温度之差；δH为测量装置产生的影响；δHcB为偏离正常工作条件的影响，包括温度影响δΔT、退磁速度影响δv、霍尔探头的温度系数影响δH(ΔT)、霍尔探头的非线性影响δH(L)以及特斯拉计的分辨力影响δf。

2.2.2 测量装置(特斯拉计)产生的不确定度

特斯拉计经计量部门检定合格，其准确度为0.5级，因此，在满量程内其最大允许误差为±0.5%。通常在1/2满量程以上使用，因而特斯拉计测量磁场强度引入的相对不确定度为：

2.2.3 偏离正常工作条件所引起的不确定度

1)Alnico永磁体矫顽力的平均温度系数β=0.0003%/℃，与Br分析方法相同，温度的影响予以忽略(即βΔT=0)，认为urel(δΔT)=0。

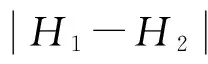
3)霍尔探头的温度系数影响δH(ΔT)：取霍尔探头的温度系数为0.01%/℃。校准时，要求测量温度控制为(20±3)℃，于是温度对HcB的影响为：

4)霍尔探头的非线性的影响δH(L)：霍尔探头的非线性可以用计算的方法进行修正。实验表明，GaAs材料的霍尔探头产生的非线性是霍尔电压的奇次函数：δH=a0V+a1V3+a2V5+…，修正后的磁场强度H′=H-δH=H-a0V-a1V3-a2V5+…。其中，ai为修正系数，V为霍尔探头输出电压。一般i取到2就可以将非线性在0.1～2.4T的范围内修正到0.10%以内。测量Alnico时，磁场强度H≤79.6kA/m，霍尔探头的非线性经修正后为0.100%，因此，可认为霍尔探头的非线性带来的不确定度影响urel(δH(L))在0.100%以内。

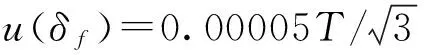
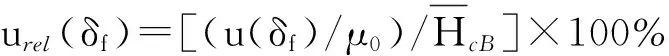
={[2.9×10-5/(4p×10-7)]/

61.50}×100%≈0.038%

综合上述可得，偏离规定的正常工作条件所引起的相对不确定度为：

urel(δHcB) =[urel2(δH(ΔT))+urel2(δH(L))+urel2(δf)]1/2

=[(0.017%)2+(0.100%)2+

(0.038%)2]1/2=0.108%

2.2.4 矫顽力HcB的扩展不确定度

HcB的合成不确定度为：

=[(0.199%)2+(0.577%)2+

(0.108)2]1/2=0.62%

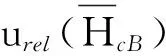
2.3 磁能积(BH)max的不确定度分析

最大磁能积(BH)max是退磁曲线上B和H乘积最大的值，即(BH)max=max{B×H}=Bd×Hd，其测量模型为：

式中，urel[δ(BH)max]=[urel2(Bd)+urel2(Hd)]1/2，Bd的相对不确定度可认为与Br相同，而Hd的相对不确定度与HcB的不确定度相同，即：urel(Bd)≈urel(Br)=0.16%，urel(Hd)≈urel(HcB)=0.62%，故：urel[δ(BH)max])=[(0.16%)2+(0.62%)2]1/2=0.64%。因此，最大磁能积的相对不确定度为：

urel2[δ(BH)max]}1/2

=[(0.467%)2+(0.64%)2]1/2

=0.79%

取置信概率p=95%，k=2，则最大磁能积(BH)max的扩展相对不确定度为：Urel[(BH)max]=k×urel[(BH)max]=2×0.79%=1.6%。

3 结论

本文从测量装置、偏离正常工作条件及测量重复性三个方面分析了影响铝镍钴磁测量的影响因素，确定了各磁参量的测量不确定度来源，通过重复试验数据的统计和数学模型的建立，逐一评估了剩磁、矫顽力和磁能积的测量不确定度。当置信概率p=95%，k=2时，扩展不确定度分别为：Urel(Br)=0.32%、Urel(HcB)=Urel(HcJ)=1.2%、Urel[(BH)max])=1.6%。

[1] Fausto Fiorillo.Measurement and Characterization of Magnetic Materials [M].Elsevier, 2004

[2] IEC 60404-5: Magnetic materials-Part 5: Permanent magnet (magnetically hard) materials- Methods of measurement of magnetic properties [S]

[3] GB/T 3217—2013: 永磁(硬磁)材料磁性试验方法 [S]

[4] 王子生，李冬云，吴琼，等.铝镍钴永磁材料磁参量测量不确定度评定 [J].电工材料，2012(4)

[5] JJF 1059.1—2012 测量不确定度评定与表示 [S].北京: 中国质检出版社，2012

[6] 叶德培.测量不确定度理解 评定与应用 [M].北京: 中国质检出版社，2013

[7] 倪育才.实用测量不确定度评定(第3版)[M].北京: 中国计量出版社，2010

中国计量科学研究院自筹基本科研业务费课题(35-JB1422)

10.3969/j.issn.1000-0771.2015.3.20