四层介质平板波导中TM波的矩阵形式及其模式本征方程

桑志文

(上饶师范学院 物理与电子信息学院,江西上饶334001)



四层介质平板波导中TM波的矩阵形式及其模式本征方程

桑志文

(上饶师范学院 物理与电子信息学院,江西上饶334001)

首先从平板波导的基础理论出发，得到三层平板波导层内TM波的转移矩阵，在此基础上进行拓展,推导出四层平板波导中的TM波的矩阵形式及其模式本征方程。

平板波导；TM波；矩阵形式；本征方程

利用多层平板介质传播光信息，其最大优势是容量大，并且平板波导在薄膜光学、电光调制等方面具有广泛的应用。利用转移矩阵的形式表示光波在多层平板介质中传播，其意义简单明了。M.玻恩和E.沃耳夫利用特征矩阵求解了多层薄膜的透射和反射问题[1]；A.Yariv等利用矩阵讨论了透镜或似透镜介质的传输问题[2]；曹庄琪利用波动方程的特解，构造出转移矩阵[3]。本文从平板波导的基础理论出发，推导出四层介质平板波导中TM波的矩阵形式及其模式本征方程。

1 介质平板波导的结构

介质平板波导的结构如图1所示，其中折射率为n1的为波导层，折射率为n0的为衬底，折射率为n2的为覆盖层，他们构成了简单的三层介质平板波导。薄膜的厚度可与光波长比较，为μm量级。其中，折射率有n1>n0>n2。如果n2=n0，则该平板波导是对称的，如果n2≠n0，则该平板波导是非对称的[3]。

2 非对称三层介质平板波导中TM导模的场分布

如图1所示，设光沿着Z方向传播，传播常数为β，对于TM偏振的(即磁场垂直于波阵面法线和分界面法线构成的入射面)的导模，磁场H=Hy，满足波动方程[3,6-7]：

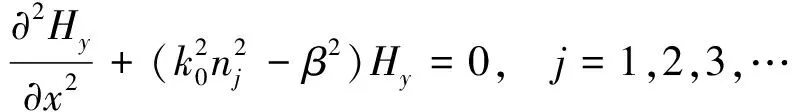
(1)

式中，k0=ω(ε0μ0)1/2=2π/λ是真空中的传播常数(或称波数)，λ为光在真空中的波长。ε0和μ0分别为真空中介电常数和真空磁导率。nj为介质的折射率。在波导层(n1)内场形成正弦曲线函数和余弦曲线函数的叠加，在覆盖层(n2)和衬底(n0)中，场是指数衰减的。其磁场的分布表示为[4]：

(2)

将上式用矩阵形式表示，则有：

(3)

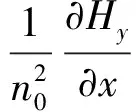
(4)

(5)

其中MTM为三层介质平板波导中TM波的转移矩阵，它仅与区间的折射率分布有关，与区间(0，h)外的折射率分布无关。

3 非对称四层平板波导中TM波的矩阵形式及其模式本征方程

图2为非对称四层平板波导的折射率分布图，其中折射率为n1，厚度为h1的区域是约束电磁场能量的导波层，覆盖层和衬底的折射率分别为n0和n3，厚度为h2，折射率为n2的区域在一定条件下也能约束电磁场能量(n1>n2>n3>n0)。

如图2所示，设光沿Z方向传播，传播常数为β，对于TM波的场分布为：

(6)

在衬底与覆盖层中磁场呈指数衰减。由转移矩阵理论[3]，可推得，此时平板波导的磁场分布方程为：

(7)

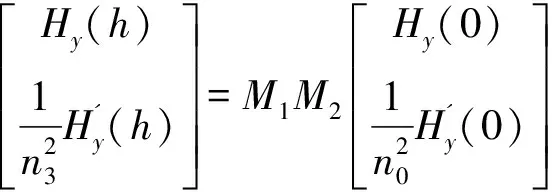
(8)

(9)

(10)

利用磁场在x=0,x=h1和x=h1+h2界面上连续，可得其模式本方程为：

(11)

4 结束语

从简单的非对称三层板波导出发，利用其波动方程以及其边界条件，导出非对称三层平板波导的转移矩阵形式，在此基础上，进一步推导出非对称四层平板波导的转移矩阵和模式本征方程。由此我们可以更加清晰地了解非对称四层平板波导中磁场的分布规律，在波导层内磁场以正弦或余弦规律分布，为了解多层非对称的平板波导中磁场分布提供了理论依据。

[1] 波恩M,沃尔夫E.光学原理[M].北京：科学出版社,1978.

[2]A.Yariv.QuantumElectronics. 2nded[M].NewYork:Wiley&Sons,1964.

[3] 曹庄琪著.导波光学中的转移矩阵方法[M].上海：上海交通大学出版社,2000.

[4] 桑志文,罗开基，况庆强.三层平板波导中TM波的转移矩阵和模式本征方程 [J].上饶师范学院学报,2004,24(3):29-32.

[5] 曹庄琪编著.导波光学[M].北京：科学出版社,2007.

[6] 方俊鑫，曹庄琪，杨傅云.光波导技术物理基础[M].上海：上海交通大学出版社，1987.

[7] 桑志文.三层介质平板波导TE波的转移矩阵和模式本征方程[J]. 上饶师范学院学报,2009，29(6)：32—35.

The Transfer Matrix and the Mode Eigenvalue Equation of TM Wave in the Four-layers Plane Waveguide

SANG Zhi-wen

(School of Physics & Electronics, Shangrao Normal University, Shangrao Jiangxi 334001，China)

From the first slab waveguide theory, acquiring the TM wave of the wave transfer matrix in the three layers waveguide field.Deduced from on the basis of the three layers planar transfer matrix.equation, it expands the TM wave transfer matrix form and mode eigenvalue equation in the four layers planar waveguide field.

slab waveguide; TM wave; matrix; eigenvalue equation

2015-11-13

江西省落地计划项目(KJLD12046)

桑志文(1962-)，男，江西玉山人，副教授，硕士，主要从事导波光学与光纤通信方面的研究。E-mail:sangzhiwen@126.com

O441.1

A

1004-2237(2015)06-0041-03

10.3969/j.issn.1004-2237.2015.06.008