一类三角矩阵的特征值反问题
2015-06-07李帅李志斌
李帅,李志斌
(大连交通大学 理学院,辽宁 大连 116028)
一类三角矩阵的特征值反问题
李帅,李志斌
(大连交通大学 理学院,辽宁 大连 116028)
对一类奇阶上三角矩阵的特征值反问题进行研究,通过两个给定特征对(λ,x),(μ,y)对矩阵的存在性及唯一性的条件进行讨论,在满足条件的前提下进行求解并给出表达式,通过数值例子验证算法的可行性.
三角矩阵;特征值;反问题
0 问题提出
矩阵的特征值反问题不仅在数值代数理论上是有意义的,而且在解决实际应用问题方面,也有举足轻重的地位[1- 4].
本文主要对如下形式的矩阵进行研究
其中,ai,bi,ci(i=1,2,…,n)∈R且ci=bi-1(i=1,2,…,n-2),c1=b0=0,n=2m-1.
问题A 给出两个非零互异实数λ,μ以及两个非零向量x=(x1,x2,…,xn)T,y=(y1,y2,…,yn)T,求n阶实矩阵J使Jx=λx,Jy=μy.
做如下约定:
(1)
(2)
(3)
(4)
(5)
(6)
(7)
1 问题A求解
1.1 当1≤i≤m-1时
由于(λ,x),(μ,y)为J的特征对,从而有
(8)
(9)
由式(8)和(9)消去ai,得
(10)
又因为
ci=bi-1,(i=1,2,…,n-2),结合式(2)、(3)、(10)可得
(11)
当i=1时,由b0=0得
(12)
当i=2时
(13)

(14)
对于式(14),若Di≠0(i=1,2,…,n-1),则xi,yi(i=1,2,…,m-1)不能同时为零,则ai,bi,ci(i=1,2,…,m-1)有唯一值.由式(14)解得
(15)
(16)
(17)
1.2 当m≤i≤n-2时
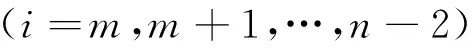
(18)
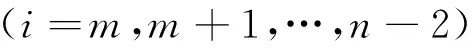
(19)
由式(18)和(19)消去ai,得
(20)
又因为ci=bi-1(i=1,2,…,n-2),结合式(2),(4)和(20)可变为
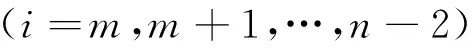
(21)
当i=m时,得
(22)
当i=m+1时,得
(23)
(24)


(25)
类似情况2.1,当Di≠0(i=1,2,…,n-1)时,ai,bi,ci(i=m,m+1,…,n-2)有唯一值,由式(25)解得
(26)
(27)
(28)
1.3 当i=n-1时
(29)
(30)
若Dn-1≠0,则an-1,bn-1有唯一值,由式(29)和(30)解得
(31)
(32)
1.4 当i=n时
①若xn≠0,yn=0,anxn=λxn则an=λ;
②若yn≠0,xn=0,anyn=μyn则an=μ;
③若xn≠0,yn≠0,anxn=λxn,从而an=λ;anyn=μyn,从而an=μ,就有λ=μ,这与λ与μ互异矛盾,从而须有xnyn=0;
④若xn=yn=0,则an解不唯一,为确保解的唯一性,需要求xn,yn不同时为零.
综上,当xnyn=0且xn,yn不同时为零时,an有唯一解,解得:
(33)
综上所述,对问题A,给出如下定理:
定理 如果以下条件满足:
(Ⅰ)Di≠0,(i=1,2,…,n-1);
(Ⅱ)xnyn=0且xn,yn不同时为零.
则问题A有解,且
(34)
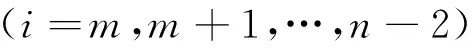
(35)
(36)
(37)
(38)
(39)
(40)
(41)
2 数值例子




c1=b0=0,c2=b1=2,c3=b2=1;


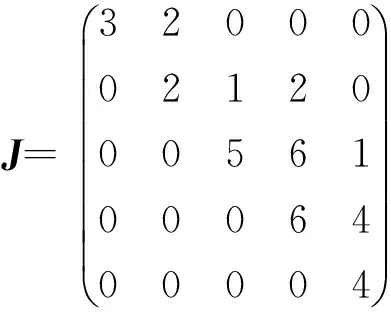
[1]李志斌,赵鑫鑫,李伟.广义Jacobi矩阵特征值反问题[J].大连交通大学学报, 2008,29(4):6- 10.
[2]戴华,姚承勇.Jacobi矩阵逆特征问题解存在的条件[J].高等学校计算数学学报,2003,25(1):40- 49.
[3]哈里曼.关于矩阵特征值正反问题的应用背景[J].新疆大学学报(自然科学版), 1997(4):26- 35.
[4]WEIWEIGU,ZHIBINLI.GeneralizedInverseEigenvalueProblemforGeneralizedSnow-LikeMatrices[C].2012InternationalConferenceonComputationalandInformationSciences(ICCIS2012),Chongqing,2012:662- 664.
Inverse Eigenvalue Problem for a Class of Triangular Matrices
LI Shuai,LI Zhibin
(School of Mathematics and Physics,Dalian Jiaotong University,Dalian 116028,China)
The eigenvalue of the a class of upper triangular matrix of odd order is studied,and the feature of existence and uniqueness of matrix via two given two characteristic pairs (λ,x),(μ,y)isdiscussed.Furthermore,thesolutionisbuilt,andexpressionisprovidedundersatisfiedconditions.Thefeasibityofthecalculationisexanimatedbyanumericalexample
triangular matrix;eigenvalue;inverse problem
1673- 9590(2015)01- 0112- 03
2014- 03- 10
国家自然科学基金资助项目(61273022)
李帅(1988-),男,硕士研究生;李志斌(1960-),教授,硕士,主要从事矩阵特征值反问题的研究
E-mail:lishuai1988214ky@163.com.
A
