面向末端刚度提升的机器人手臂关节角路径优化
2015-06-07沙智华刘延辉宿崇马付建刘宇张生芳
沙智华,刘延辉,宿崇,马付建,刘宇,张生芳
(大连交通大学 机械工程学院,辽宁 大连 116028)
面向末端刚度提升的机器人手臂关节角路径优化
沙智华,刘延辉,宿崇,马付建,刘宇,张生芳
(大连交通大学 机械工程学院,辽宁 大连 116028)
针对六自由度串联关节机器人手臂,采用D-H法对手臂的操作空间进行了描述,得到了正、逆解运动学模型,建立了机械臂运动学方程.在各运动角度优化指标下,优选末端关节角度来增加手臂的刚度和稳定性,从而实现机械臂路径规划的优化.引入目标函数和遗传算子,提出了一种基于遗传算法的多目标机械臂路径规划算法.通过Matlab工具箱进行仿真验证,证明了该算法的有效性与可行性.
机器人制造系统;末端刚度;路径规划;遗传算法;多目标优化
0 引言
在航空航天、高铁、造船等制造领域,大型构件的装配连接中多采用螺接和铆接的机械连接方式,这就需要在这些大型构件上加工大量的精密装配连接孔.由于这些构件整体尺寸巨大,难以装夹在机床上进行加工,因此机器人制孔系统以其结构简单、效率高、柔性高、适应场合广泛等突出优点,成为国内外大型构件孔群加工领域最为广泛的制孔方式[1].由于这些大型构件上连接孔的数量巨大,机械臂的路径规划问题就成为影响加工效率的首要问题,所以需要对连接孔加工路径进行规划.
目前,针对机械人机械臂路径规划的方法非常多,主要有全局路径规划和局部路径规划.全局路径规划有自由空间法、可视图发和栅格法,这些方法计算量大和实时性差等缺点.在局部路径规划中,贾庆轩等[2]采用基于A*算法的机械臂路径规划算法,在机械臂的空间进行路径搜索.徐海黎等[3]采用EGICA算法对机器人的关节进行了轨迹,同时以最优能量和最优时间为目标的路径优化.Duguleanam等[4]提出了一种基于Q-learning双神经网络的机械臂路径规划算法,这种方法具有良好的平均速度和目标达成率.这些路径规划方法从时间、能量、效率、空间避障等进行研究,但是缺乏对机器人末端刚度的考虑.
在机械孔加工过程中,多关节串联工业机器人本身刚性较差,加上末端执行器的重量,会进一步降低整个制孔系统的刚度,这会直接影响制孔的形位精度和加工质量.因此,在孔加工过程中如何保证机器人制孔系统的末端刚度十分重要.本文以六自由度机器人手臂为研究对象,建立运动学方程,基于遗传算法提出一种优选关节角的机械臂路径规划方法,增加机器人的末端刚度.
1 机器人运动方程建立
1.1 运动学正解
机械臂采用6自由度工业机器人机械臂(如图1所示),该机械臂是关节式串联结构,它由一个固定底座和六个活动旋转连杆组成.
为了方便运动学求解,采用传统的D-H法[5]对机械臂运动学模型进行描述.建立了各关节坐标系(如图1中),从X0-Z0到X6-Z6为机械臂基础坐标系、机械臂各关节坐标系、机械臂末端坐标系.用矩阵变换可以实现第i-1坐标系和第i坐标系之间的关系,用矩阵Ai表示其关系式为:
(1)
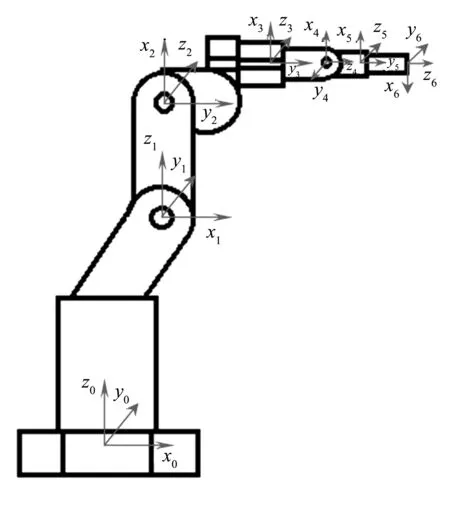
图1 机器人机械臂示意图和坐标系
根据式(1),依次建立各关节坐标系相对于前一关节坐标系变化矩阵Ai, 再按顺序右乘各关节变化矩阵,就能够得出机械臂末端相对于基础坐标系的位姿矩阵:
(2)
根据图1机械臂的物理参数和坐标系的定义可以得到D-H参数表如表1所示.
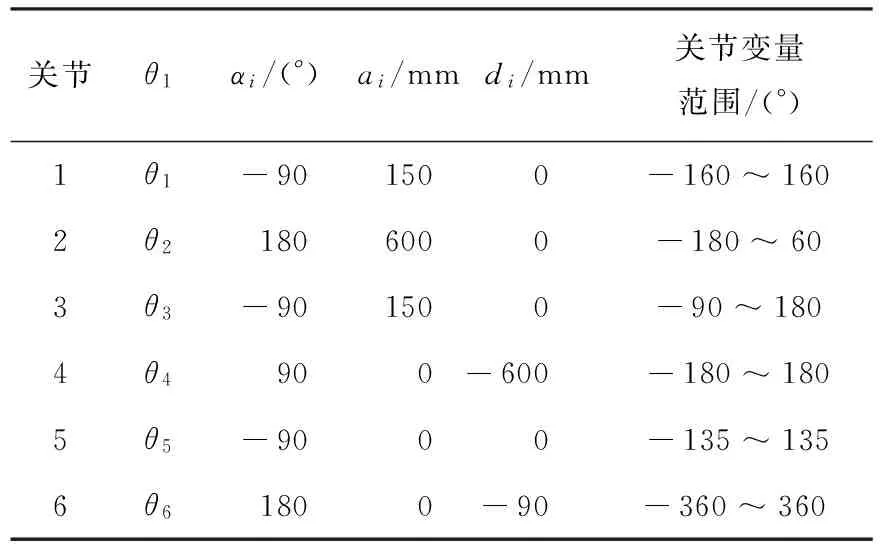
表1 D-H参数
1.2 运动学逆解
机器人末端实现运动是通过控制机械臂的各个关节转动来实现的,为了保证机械臂末端的位姿能够达到指定待加工孔和按照一定轨迹运动,必须进行运动学逆解计算.逆向运动学的求解过程是根据已知的机械臂末端相对于基坐标系的位姿,求各关节的旋转变量.运动学逆解的求解过程要比正解求解过程复杂得多,在求解时需要考虑可解性、解的存在性和多重解等问题.
采用D-H法建立的机械臂运动学模型,通常利用解析法进行求解,解析法求解机器人运动学逆解的过程就是依次求解各运动关节的转动变量.求解关节变量θ1,θ2,θ3,θ4,θ5,θ6的逆运算过程较多也比较成熟,在这里不在进行阐述.
应用机械臂逆解的求解过程,求解各个方程的参数θn1,θn2,θn3,θn4,θn5,θn6,θn7,θn8,产生8组不同的关节变量值的可行解(超出关节运动范围舍去),从解集中将选择一组解作为机械臂各关节的逆解.逆解的求解过程为接下来的路径规划工作奠定了基础.
为实现机器人末端刚度优化,本文在各个关节界限的约束下,求取机械臂各连杆从初始关节角变化到终点关节角时的一系列中间关节角[6],在得到中间关节角的同时,需要满足机械臂末端的刚度要求,实现路径的最优化.
2 面向末端刚度的优选关节角
机器人机械臂主要有机械臂杆和关节组成,具有高负载自重比、结构紧凑、功耗低、操作灵活的特点.但是,在具有诸多优点的同时,机械臂在加工中也有着明显缺陷,机械臂刚度低、易产生变形,从而严重限制了机械臂的加工应用,这就需要通过角度的优化提升机械臂的刚度.
机械臂在材料和构型确定的情况下,其刚度与部件的体积和质量正相关.由于空间机械臂的受力大小和自重的限制,机械臂臂杆的横截面面积从基座到末端依次变小,从而使得机械臂末端刚度最小,也因此影响机械臂的整体刚度.
根据静力学的要求,这里假设全部的连杆为刚性体.为了简单表述,这里将各个关节的刚度用弹簧系数ki进行表示,因此机械臂的刚度矩阵K就可以表示为:
K=diag(k1,k2,k3,k4,k5,k6)
由机械壁正解运动学末端执行器相对于基础坐标的变换矩阵为A,则可以得到机械臂末端刚度矩阵Ke:
这就是机械臂的静刚度模型[7].
在机械臂静刚度模型中可以看出,机械臂的末端刚度取决于各个连杆之间的转动关节的刚度和机械臂相对于基础坐标系的坐标变换矩阵,机械臂在各关节刚度一定的情况下,调整机械臂末端变化矩阵(也就是机械臂形位)增加机械臂的刚度.
为提升末端刚度,这里通过优选关节角,面向末端刚度的优选关节角算法流程图如图2所示.

图2 优选关节变量流程图
已知机械臂在初始位置时的各关节角度(如表1所示) 和目标点X的空间位置.
首先设定机械臂末端在X处的期望姿态.根据目标点的空间位置和机械臂末端期望姿态,利用多关节运动学逆解公式(3~8)获得各关节终点角,结果为多解,有些解会超出关节的运动范围,需要舍去.
再次通过关节角优化提升末端臂杆刚度和增加稳定性.根据本文机械臂的选型,优选第3和第5关节角,使它们相对初始关节角度变化最小,从而提升机械臂末端臂杆的刚度.
计算公式如下:
式中:n=1,2,3,4,5,6,7,8.
最后在满足整体角度变化最小的情况下,实现机械臂对孔群进行加工路径的优化.在3和5关节局部优化解集中,采用1、2、4、6关节总变化量为最小选出最优解.这样就使得机械臂运动中消耗更低的能量.
3 关节角路径规划算法
在机械加工中,有很多路径规划的方法,连续空间多目标函数的优化问题多使用传统的路径规划方法,而机械臂路径规划问题主要解决的是离散空间组合优化问题,传统的方法难以解决这类存在“组合爆炸”空间解的问题.而遗传算法[8]则提供了系统通用框架来解决这类复杂的问题.本文通过使用遗传算法中的TSP(旅行商问题)对加工路径进行优化.TSP优化求解过程需要编码、初始化孔群、确定适应度函数和遗传操作等.TSP算法流程图如图3所示.
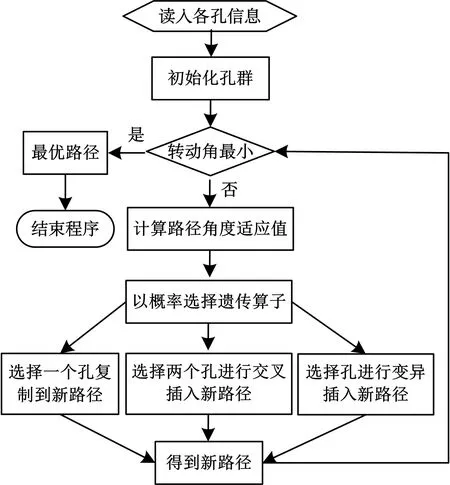
图3 TSP算法流程图
(1)编码
在读入孔群信息之前,需要确定变量的编码方式,在遗传算法TSP问题[9]中不适合二进制表达,这里以待加工孔坐标点的遍历次序作为算法编码,给每一个孔分配一个1到n的序列,这种编码方式在满足TSP问题约束条件下,还能保证每一个待加工孔只经过一次,同时还也能保证不形成回路.
(2)初始化孔群
选择N个孔作为规模大小,随机选取N个孔组成的初始化孔群,生成初始解空间.在实际孔加工中,有些孔与孔之间存在特定的加工顺序,以满足特定要求的解中再选取孔群,这使得算法具有更快的收敛性.
(3)适用度函数
机械臂在三维空间中进行路径规划,各关节在工作空间做旋转运动,所有关节的累积转动角度应在满足优选末端关节角最优解下尽可能小.因而把累积转动角作为优化目标[10].最小累积转动角度可用f(θ)表示:
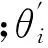
(4)遗传算子的选择
算法操作类型包括三种:选择(复制)操作、交叉操作和变异操作.
选择操作采用与适应度函数值成正相关的概率方法,从孔群中选择优良个体,优先参加下一代的优化,即使优选孔复制到路径中,产生新的路径.
交叉操作是在具有相交点的两条路径上,把交点处后边的子路径串相互交换,形成两个新的路径.
变异操作是在已经形成的路径中随机选择几个孔(2~N-1)进行交换,从中选择最优的路径作为新的路径.
(5)确定终止条件
优化过程需要反复执行(3)和(4),直到路径转动角度最小,实现路径最优化.
4 算法验证
利用计算机辅助设计软件Matlab[11],构建机械手臂的实体模型,并读取模拟程序所产生的各臂杆的关节角度资料,以进行运动模拟.由Matlab的绘图的功能,可清晰地展现出优化的结果.
本路径规划仿真有40个孔,其坐标值如图4(a)所示,孔的加工尺寸相同、加工精度也相同,在孔的加工过程中,不需要进行换刀等操作,只要找到它行走的一条角度变化值最小的路径.
遗传算法参数为孔的坐标40个、进化迭代为1 000代、交叉概率为0.7、变异概率为0.4,进行Matlab仿真,仿真结果如图4所示.
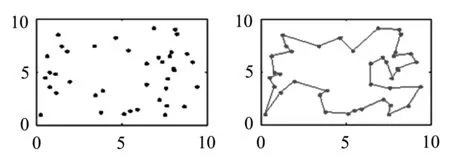
(a)待加工孔坐标 (b)优化前路径
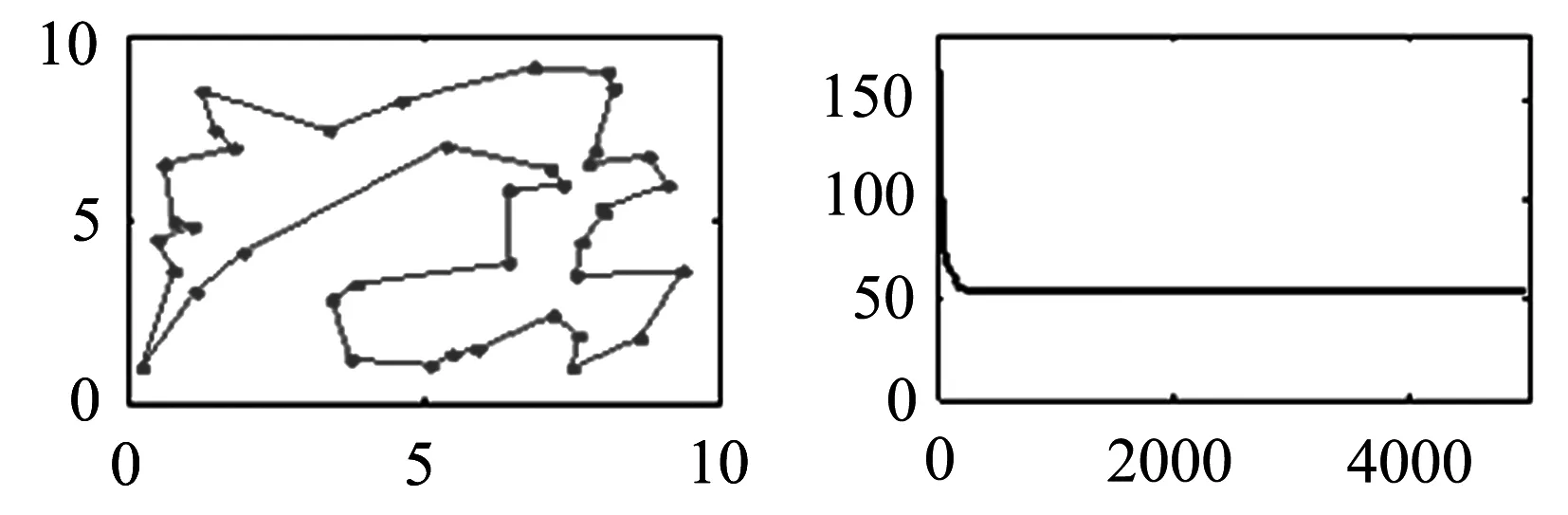
(c)优化后路径 (d)算法收敛过程
图4 仿真优化
采用TSP算法,对40个孔群进行迭代优化,最终找到最优路径.在如图4(a)所示可以看到,这个孔群分布是没有规律的,对称性也很差,用一般传统的处理方法难以得到最优路径.如果采用随机产生路径的方法,得到的路径转动角很大,空行程浪费也很多.从如图4(b)所示,随机产生路径得到的转动角度为89.134 9,而采用TSP算法转动角度相对较小,角度变化值只有53.189 5(如图4(c)所示),转动角度优化接近60%,优化结果明显.如图4(d)所示,是遗传算法运行过程中得到的总变化角度随遗传进度的变化趋势.一般而言,运用遗传算法求解路径优化问题时,优化结果总是先变化快最后趋于平缓.本文的仿真结果也是一样,在遗传算法开始运行时,优化效果显著,之后趋于平缓.
通过Matlab仿真实验数据表明,TSP算法在考虑优选末端角度的情况下,采用转动角度最小进行路径优化,具有有效性与可行性.
5 结论
针对六自由度串联关节型机械臂进行正、逆运动学分析,建立运动学方程,为机械臂路径优化提供理论基础.
机械臂末端臂杆在进行加工过程中承受负载和自重的作用,其刚度较低,影响加工质量.为解决这个缺陷,提出采用优选关节角的方法,解决机械手臂末端的刚度和稳定性的问题.同时以最小转动角为优化目标下,采用遗传算法对路径进行规划,能够大幅度提高孔群加工的效率.
基于TSP的模型,建立了孔群多目标路径优化模型,采用Matlab工具对随机产生的孔群进行优化求解,多次迭代找到最优路径,优化结果明显,优化过程收敛性强,实现了路径优化.证明方法在面向末端刚度提升的关节型机械臂路径规划中具有可行性、通用性和有效性.
[1]DEVLIEG R.High-accuracy robotic drilling milling of 737 inboard flaps[J].SAE Int.J.Aerosp.,2011,4(2):1373- 1379.
[2]贾庆轩,陈钢,孙汉旭,等.基于A* 算法的空间机械臂避障路径规划[J].机械工程学报,2010,46(13):109- 115.
[3]徐海黎,谢祥荣,庄健,等.工业机器人的最优时间与最优能量轨迹规划[J].机械工程学报,2010,46(9):20- 25.
[4]DUGULEANAM,TEIRELBARA.Obstacle avoidance of redundant manipulators using neural networksbasedreinforcement learning[J].Roboticsand Computer-IntegratedManufacturing,2012,28(2):132- 146.
[5]汪首坤,邸智,王军政,等.基于A*改进算法的机械臂路径规划[J].北京理工大学学报,2011,31(11):1303.
[6]谭晓东,刘鑫,赵岩.PUMA- 56机械手虚拟装配过程中的视觉分析和变化计算的研究[J].组合机床与自动化加工技术,2010(1):28- 30.
[7]曲巍崴,候鹏辉,杨根军,等.机器人加工系统刚度性能优化研究[J].航空学报,2013(12):2814- 2825.
[8]凌玲,王青青,张正义,等.基于改进遗传算法的箱类零件加工路线优化问题研究[J].组合机床与自动化加工技术,2009(1):76- 78.
[9]周正武,丁同梅.基于TSP和GA孔群加工路径优化问题的研究[J].组合机床与自动化加工技术,2007(7):30- 32.
[10]朱华炳,程翔宇,唐自玉,等.多目标遗传算法适应度函数权重设置的改进[J].组合机床与自动化加工技术,2007(4):11- 14.
[11]柳敏飞.基于MATLAB遗传算法的齿轮减速器的优化设计[J].组合机床与自动化加工技术,2009(8):36- 38.
End Stiffness Lifting Oriented Path Planning for Manipulator Joint Angle Optimization
SHA Zhihua,LIU Yanhui,XU Chong,MA Fujian,LIU Yu,ZHANG Shengfang
(School of Mechanical Engineering, Dalian Jiaotong University,Dalian 116028,China)
To ensure the end stiffness of the robot during the holing process,the 6-FOD series joint manipulator is studied,and the manipulation space of the manipulator with D-H method is described to obtain its positive solution and inverse solution kinematic model and equations.Taking the movement angle as optimization index,the end joint angles are selected to increase the manipulator stiffness and stability.With suitable objective function and genetic operators,a multi-objective manipulator path planning algorithm is proposed based on genetics algorithms.According to the simulation result with the help of MATLAB toolbox,the effectiveness and feasibility are verified.
robotic manufacturing system;end stiffness;path planning;genetic algorithm;multi-objective
1673- 9590(2015)01- 0038- 05
2014- 03- 29
辽宁省高等学校优秀人才支持计划资助项目(LJQ2012039);辽宁省“百千万人才工程”资助项目(2012921053);大连市科学技术基金资助项目(2013J21DW011K);中国博士后科学基金资助项目(2013M530901)
沙智华(1973-),女,教授,博士,主要研究方向为虚拟制造与网络制造
E-mail:zhsha@djtu.edu.cn.
A
