基于充电策略的纯电动公交车辆调度优化
2015-06-07唐晓宇赵长相
李 军,唐晓宇,赵长相
(中山大学 工学院 智能交通研究中心,广东 广州 510006)
基于充电策略的纯电动公交车辆调度优化
李 军,唐晓宇,赵长相
(中山大学 工学院 智能交通研究中心,广东 广州 510006)
考虑充电区间、充电速率、电池核电状态、发车策略等综合因素,提出了以最小化车辆数为目标的单线路单充电站的纯电动公交车辆调度算法。该算法采用车队整体优化的方法,使得营运的车辆数最小,并达到每辆车发车次数的均衡。以东莞松山湖公交线路为例,分析了线路发车时刻、充电速率、车辆耗电对车辆数及单车发车次数的影响,并和常规公交车辆调度算法进行比较,结果表明:改进发车策略有效地减少了所需车辆数,且车辆利用率均衡,达到了最小化车队成本的目的。
车辆工程;纯电动公交;公交调度;电池核电状态;充电策略;动态规划
0 引 言
纯电动车辆具有污染小、能量来源多样化等特点,可以缓解城市交通污染,越来越受到重视。但纯电动汽车动力电池续驶里程有限、充电时间较长,导致纯电动车辆在具体应用方面受到严重制约。在目前动力电池无法提供更长续驶里程的情况下,如果能够快速为电池补充电量,即可在一定条件下解决了电动汽车续驶里程不足的致命弱点[1]。纯电动车辆调度需要考虑续驶里程及充电时间限制[2],常规公交车辆调度的模型不适用于电动公交车辆调度,因此,需建立适用于电动公交车辆的调度模型。
电动汽车的续驶里程与动力电池容量、单程行驶耗电量等因素有关,而时刻表、充电策略等决定着充电时间的大小。电动公交的调度问题中,公交行驶路线、行车时刻表及电动车辆的车型等因素多为已知,主要优化电动汽车充电策略,合理调度车辆,降低最小车辆数,进而减少运营成本。国内外关于充电策略的研究,主要集中在管理电动汽车充电行为,减轻其对电网的负面影响[3];电动汽车充电模式的选择,及充电设施的选址定容;充电策略的变化对电动汽车动力电池的影响。笔者仅从电动公交运营的角度考虑,假设电动汽车充电站容量可以充分满足电动公交车辆的充电需求,忽略电动汽车充电行为对电网的影响。现行电动汽车充电模式,主要包括整车常规充电、整车快速充电和更换电池三类[4]。其中快速充电,可以提供短时充电服务,充电时间短,适于电动公交车辆补充电量,但对电池损害较大,对技术及安全性要求较高。通过电池快速充电控制仿真模型[5],发现选择适宜的充电速率,控制电动汽车的电池核电状态(SOC)在一定范围,可延长电池寿命。对电池组实行浅充浅放时,电池内阻小,能量转化率高,不会出现过充过放,循环寿命长,但此种情况会造成谷电利用率较低。当电动公交车辆行驶路线较短,单程耗电量较小时,可采用间歇补电[6]的方式,以小倍率为电池组补充电量,即车辆每完成一个行驶班次后利用等待时间充电,使电池组保持在“半充半放”状态下工作。
根据车场数目,公交车辆调度问题可分为单车场车辆调度(SDVSP)和多车场车辆调度(MDVSP)[7]。在应用中,车辆调度问题常被描述为整数线性规划(ILP)问题,先构造一个较大的解空间,然后利用启发式方法进行优化,但求解耗时较多[8]。SDVSP被描述为近似指派问题,采用先生成班次序列然后再组合的策略进行求解,结果较好[9-10]。MDVSP调度模型主要分为多商品流模型和集分割模型。模型的求解算法包括拉格朗日松弛启发式算法、列生成算法、搜索树方法、分值定价法等,但多数只能应用于对较小规模问题的求解,启发式算法仍然是解决公交车辆调度问题的重要方法[11-13]。求解MDVSP问题时,可基于逆差函数法采用先进站先发车方法构建班次序列[14],以实现需用车队规模最小的优化目标。电动公交车辆的调度更加复杂,不仅要满足常规公交车辆调度的约束条件,还需增加续驶里程与充电时间的限制条件[2],现行的解决方法多将电动公交车辆调度问题划分为两阶段求解,分别为有续驶时间约束的车辆调度问题和有充电时间约束的车辆调度问题,对第一阶段的解进行优化得到最终的优化解[15],但这样可能导致第二阶段的方案部分丧失了获得最优化的机会。
笔者研究单线路单站点的纯电动公交车辆运营问题,假设充电站与终点站重合,在运营过程中动力电池采用“间歇补电,浅充浅放”的方式补充电量,考虑考虑车辆续驶里程及充电时间的双重限制,优化充电策略,改进发车算法,实现车辆数最小。并用常规公交代替电动公交,保持其他条件不变,得到该条件下所需要的车辆数,与纯电动公交车辆的调度结果进行对比。
1 纯电动公交调度模型
纯电动公交车辆由于动力电池续驶里程及充电时间的局限性,在调度时需重点关注纯电动公交车辆的SOC变化。公交行驶路线、线路站点的设置,决定车辆的单程行驶时间、单程行驶耗电量,影响车辆类型的选择、动力电池的额定电量、最大续驶里程。线路时刻表,是车辆调度的核心,确定各车次的发车时间。充电设施的选址及容量,则直接影响电动公交车辆充电模式的选择及充电时间的大小。
1.1 电动公交充电策略
由于纯电动公交受到电池续航能力的限制,公交线路长度较短,车辆单程行驶耗电量较小。动力电池SOC较高时会减少电池寿命,SOC较低时电动汽车续驶里程不足,而电池组维持在“半充半放”的状态下工作时,可在满足电动汽车续驶里程的要求的基础上,延长电池循环寿命。综合考虑,笔者的充电策略具体为:
1)采用“浅充浅放”的充电模式,避免电池SOC经常处于较高或较低状态,减缓电池衰减并避免电池续驶里程不足。
2)在整个运营过程中,分别设置动力电池SOC工作区间的上限SOCmax下限SOCmin,且SOCmax<1,SOCmin>0。
3)车辆每完成一个行驶班次后可利用等待时间充电,当某车辆SOC达到SOCmax时,车辆终止充电,或者当距离下个行驶班次的发车时刻,剩余时间大于或等于发车准备时间Td时,该车辆SOC电量可以足够完成单次行驶任务且整个过程中车辆SOC不低于下限,按照指定的发车策略,该车辆恰被选中执行车次任务,可终止充电,执行车次任务。
1.2 相关变量及假设
为描述纯电动公交运营规划中车辆的状态变化,定义下列变量,如表1。
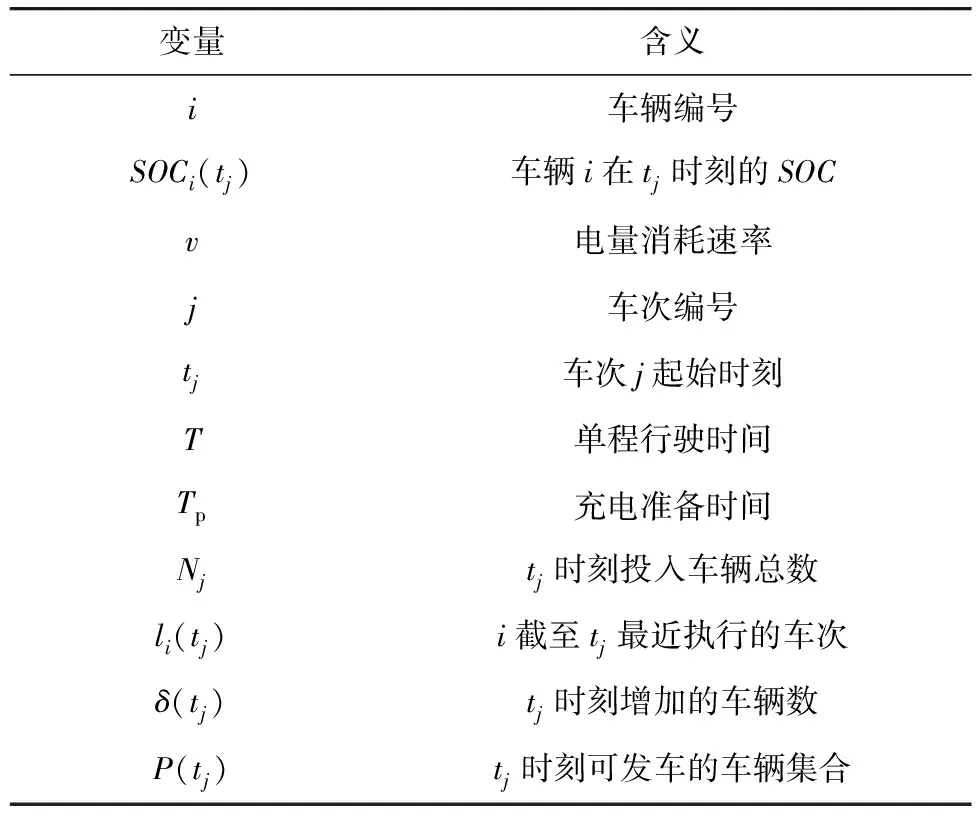
表1 纯电动公交运营规划相关变量
为简化问题,笔者做出如下假设:
1)公交线路站点、时刻表、车辆类型、充电站等相关信息为已知条件;
2)电动公交充电需求可被充分满足,即任意车辆经过充电准备,即可充电,无需排队等待车位;
3)采用恒流充电,充电速率为c,充电量和充电时间呈线性关系;
4)当天行车任务开始时,车场内所有车辆SOC均为SOCmax。
1.3 发车限制条件
某车辆若执行车次任务,则该车辆首先需满足最低电量要求,即在该车次的发车时刻,车辆SOC不小于SOCmin与单程行驶耗电量之和,如式(1):
SOCi(tj+1)≥SOCmin+v·T
(1)
同时还应满足时刻表的限制,即车辆上次执行的车次的结束时刻与发车准备时间Td之和应不大于该车次的发车时刻,如式(2):
tli(tj)+T+Td≤tj+1
(2)
1.4 车辆状态变化过程
在车辆调度运营期间,将车辆i在某时刻的状态分为5种,如表2。

表2 运营期间电动公交车辆状态
1.4.1 充电条件
当车辆上次执行的车次的结束时刻与tj+1的间隔大于Tp,则表明在tj+1时刻车辆可进行充电作业,如式(3):
tli(tj)+T+Tp≤tj+1
(3)
1.4.2 执行条件
当车辆上次执行的车次的结束时刻与tj+1的间隔大于Tp和Td之和,则表明车辆可进行充电作业,且当该车辆电量满足式(1)时,可被挑选执行车次j+1,如式(4):
tli(tj)+T+Tp+Td≤tj+1
(4)
1.4.3 车辆转移方程
针对表2中车辆的5种状态,分别给出下一个发车时刻的车辆状态。
1)车辆xi(tj)=0
在tj+1时刻,车辆i状态变化如下:
若tj+T>tj+1,即车辆i仍在执行车次j,则xi(tj+1)=1;若tj+T ①若同时满足式(1)、式(2)、式(4),即车辆i结束车次j行车任务后,可进行充电作业,并且满足发车时刻及最低电量限制,利用式(5)计算车辆SOC,同时i∈P(tj+1),xi(tj+1)=0: SOCi(tj+1)=SOCi(tj)-v·T+c·[tj+1-(tj+ T+Tp+Td)] (5) ②若满足式(1)、式(2),不满足式(4),即车辆i结束车次j行车任务后,满足发车时刻及最低电量限制,但无足够时间进行充电作业,利用式(6)计算车辆SOC,同时i∈P(tj+1),xi(tj+1)=0: SOCi(tj+1)=SOCi(tj)-v·T (6) ③若满足式(3),不满足式(1)或式(2),即车辆i结束车次j行车任务后,可进行充电作业,但不满足发车时刻或最低电量限制,则xi(tj+1)=2。 ④若不满足式(3)、且不满足式(1)或式(2),即车辆i结束车次j行车任务后,不满足发车限制,且无足够时间进行充电作业,则xi(tj+1)=3。 2)车辆xi(tj)=1 在tj+1时刻,车辆i状态变化如下: 若tli(tj)+T>tj+1,车辆i仍在执行车次li(tj),此时xi(tj+1)=1;若tli(tj)+T ①若同时满足式(1)、式(2)、式(4),即车辆i结束车次li(tj)行车任务后,进行充电作业,并且满足发车时刻及最低电量限制,利用式(7)计算车辆SOC,同时i∈P(tj+1),xi(tj+1)=0: SOCi(tj+1)=SOCi(tj)-v·(tli(tj)+T-tj)+ c·[tj+1-(tli(tj)+T+Tp+Td)] (7) ②若满足式(1)、式(2),不满足式(4),即车辆i结束车次li(tj)行车任务后,满足发车时刻及最低电量限制,但无足够时间进行充电作业,利用式(7)计算车辆SOC,同时i∈P(tj+1),xi(tj+1)=0。 ③若满足式(4),不满足式(1),即车辆i结束车次li(tj)行车任务后,可进行充电作业,但不满足最低电量限制,则xi(tj+1)=2。 ④若满足式(3)、且不满足式(1)、式(4),即车辆i结束车次li(tj)行车任务后,可进行充电作业,但不满足电量限制,则xi(tj+1)=2。 ⑤若不满足式(3)、且不满足式(1)或式(2),即车辆i结束车次li(tj)行车任务后,不满足电量或发车时刻限制,且无足够时间进行充电作业,则xi(tj+1)=3。 3)车辆xi(tj)=2 在tj+1时刻,车辆i状态变化如下: ①若满足式(1)、式(2),即车辆i在tj+1时刻,满足发车限制,利用式(8)计算车辆SOC,同时i∈P(tj+1),xi(tj+1)=0: SOCi(tj+1)=SOCi(tj)+c·[tj+1-(tj+Td)] (8) ②若满足式(2)、不满足式(1),即车辆i在tj+1时刻,不满足最低电量限制,xi(tj+1)=2。 ③若不满足式(2),即车辆i在tj+1时刻,不满足发车时刻限制,利用式(9)计算车辆SOC,若SOCi(tj+1) SOCi(tj+1)=SOCi(tj)+c·(tj+1-tj) (9) 4)车辆xi(tj)=3 在tj+1时刻,车辆i状态变化如下: ①若满足式(1)、式(2)、式(4),即车辆i在tj+1时刻,可进行充电作业,且满足发车限制,利用式(10)计算车辆SOC,同时i∈P(tj+1),xi(tj+1)=0: SOCi(tj+1)=SOCi(tj)+c·[tj+1-(tli(tj)+T+ Tp+Td)] (10) ②若满足式(1)、式(2),不满足式(4),即车辆i在tj+1时刻,满足发车限制,但无足够时间进行充电作业,利用式(11)计算车辆SOC,同时i∈P(tj+1),xi(tj+1)=0: SOCi(tj+1)=SOCi(tj) (11) ③若满足式(4),不满足式(1),即车辆i在tj+1时刻,可进行充电作业,但不满足最低电量限制,则xi(tj+1)=2。 ④若满足式(3),不满足式(1)、式(4),即车辆i在tj+1时刻,可进行充电作业,但不满足最低电量限制,xi(tj+1)=2。 ⑤若不满足式(3),且不满足式(1)或式(2),即车辆i在tj+1时刻,不满足发车限制,且无足够时间进行充电作业,xi(tj+1)=3。 5)车辆xi(tj)=4 在tj+1时刻,车辆i状态变化如下: ①若满足式(2),即车辆i在tj+1时刻,满足发车时刻限制,利用式(11)计算车辆SOC,同时i∈P(tj+1),xi(tj+1)=0。 ②若不满足式(2),即车辆i在tj+1时刻,不满足发车时刻限制,xi(tj+1)=4。 1.5 电动公交优化算法 单条线路条件下的常规公交车辆调度,不允许跨线调度和插入空驶车次,可利用先到站先发车(FIFO)策略,构造车次链,从而得到该线路所需要的最小车辆数[14]。笔者在车辆满足时刻表及电量限制的基础上,将FIFO发车策略应用于电动公交车辆调度,调度过程如下: 1)当j=1,由车辆i=1执行车次1; 2)当j=j+1时,从集合P(tj+1)中挑选出li(tj)最小的车辆执行该车次,δj+1=0; 3)如果在tj+1时刻,集合P(tj+1)为空集,则增加一辆新车,δ(tj+1)=1,由新增加的车辆执行车次j+1,截至tj+1时刻,由公式(12)计算所需的车辆数; 4)重复上述步骤,直至完成当天所有行车任务,即j=n,调度所需要的车辆总数等于Nn: Nj+1=Nj+δj+1 (12) 从提高电动公交车辆的电量利用率、均衡车队中车辆状态的角度,提出改进发车算法(OPT)调度电动公交车辆,算法流程如图1。 图1 优化算法流程 具体车辆调度过程如下: 1)当j=1,由车辆i=1执行该车次; 2)当j=j+1时,从集合P(tj+1)中挑选出总发车次数及车辆编号最小的车辆执行该车次,δj+1=0; 3)如果在tj+1时刻,集合P(tj+1)为空集,则增加一辆新车,δ(tj+1)=1,并将车队初始规模更新为截止到j+1车次需要的车辆总数Nj+1,返回步骤1; 4)重复上述步骤,直至完成当天所有行车任务,即j=n,调度所需要的车辆总数等于Nn。 2.1 案例数据 以东莞松山湖公交线路为例,该线路为环形线路,全程行驶时间约为66 min,车辆仅在终点站可以补充电量。电动车辆电池组[6]相关信息如下:电池额定容量336 V/250 Ah;电池充电准备时间及发车准备时间均为10 min。 为研究时刻表、SOC区间及单程耗电量对电动公交车辆调度的影响,共做了7组实验,各实验条件如表3。首、末班车时刻分别为7∶00和20∶00,高峰时段为8∶00—9∶00,11∶00—12∶00,18∶00—19∶00。 表3 实验条件设置 2.2 公交车辆调度结果 利用上述两种发车策略,改变充电速率,调度电动公交(EV)车辆,得到不同条件下的最小EV车辆数及车队运营状态。同时保持公交线路站点、时刻表条件不变,调度常规公交(CV)车辆,得到最小CV车辆数及车队运营状态。 上述实验的调度结果如表4。 表4 调度结果(FIFO/OPT/CV) 2.3 结果讨论 2.3.1 单组实验分析 以实验1为例,由表4可以看出: 1)当选用同种充电速率,OPT发车策略需要的车辆数更小,且车队最大与最小发车次数之差较小,说明OPT发车策略较优,车辆利用率高。 2)采用同种发车策略,增大充电速率,车辆数会减少,车队最大与最小发车次数之差也缩小,而充电速率较大,如1.0 C或1.5 C,最小车辆数相同。说明充电速率直接影响车队规模,但当充电速率足够大时,最小车辆数由其他因素决定。 3)当充电速率为1.0 C或1.5 C,采用OPT策略,所需要的EV数目比CV多1辆,同等条件下,CV数目仅由线路时刻表决定,说明在时刻表已知时,可通过提高充电作业效率,减小充电准备时间,降低充电时间的限制,从而减小最小车辆数。 2.3.2 时刻表影响 为分析时刻表对电动公交车辆调度的影响,对比实验1~实验3的调度结果可知:制定合适的线路时刻表对车辆调度至关重要,当车辆发车间隔较小时,车辆数目完全由时刻表限制,当车辆发车间隔较大时,车辆充电时间充足,车次总数少,较小的充电速率也可能得到与CV相同的车辆数。 2.3.3SOC区间影响 为分析SOC区间对电动公交车辆调度的影响,对比实验1、实验4及实验5的调度结果,选用OPT发车策略调度车辆,0.3 C充电速率补充电量,SOC利用区间较大时,最小车辆数会减少,而采用大充电速率补充电量,结果完全相同。说明增大SOC区间,当充电速率较小时,车辆可更多的满足发车电量限制条件,从而减少最小车辆数。当SOC区间范围相等时,最小车辆数相同,但采用FIFO策略调度车辆时,SOC位于中等区间,车辆最大和最小发车次数之差会缩小,车队状态更加均衡。 2.3.4 单程耗电量影响 为分析单程耗电量对电动公交车辆调度的影响,对比实验1、实验6和实验7的调度结果,在充电速率较小时,增加车辆的单程耗电量, OPT策略较FIFO策略对最小车辆数的优化效果减弱。但充电速率足够大时,最小车辆数仍相同。3组实验的车辆单程耗电量差距不多,因此当充电速率增至1.5 C时,可以得到相同的最小车辆数。 OPT发车策略旨在缩小车辆发车次数差异, 平衡车队中车辆运行状态,采用该发车策略调度车辆,需要的车辆数目小于传统FIFO发车策略,在充电速率较小时,表现更为明显。 当电池充电策略固定时,时刻表直接决定最小车辆数,且车辆发车间隔过大或过小时,EV数目均可能与CV数目相同。 当时刻表一定时,电池SOC区间及充电规则是最小车辆数目的重要决定因素。充电速率较小时,可通过调整发车策略,优化最小车辆数,而当充电速率较大时,决定车辆数目的因素则是时刻表、充电规则等,与采取的发车策略无关。 [1] 康继光,卫振林,程凡明.电动汽车充电模式与充电站建设研究[J].电力需求侧管理,2009,11(5):64-66. Kang Jiguang,Wei Zhenlin,Cheng Fanming.Research on electric vehicle charging mode and charging stations construction [J].Power Demand Side Management,2009,11(5):64-66. [2] Robert B,Ahmed E.Modeling transit trip time using archived bus dispatch system data [J].Journal of Transportation Engineering,2003,130(1):56-67. [3] 张志伟,顾丹珍.电动汽车智能充电策略研究[J].中国电力,2013,46(6):91-95. Zhang Zhiwei,Gu Danzhen.Study on strategies for smart charging of Electric Vehicles [J].Electric Power,2013,46(6):91-95. [4] 姚伟峰,赵俊华.基于双层优化的电动汽车充放电调度策略[J].电力系统自动化,2012,36(11):30-37. Yao Weifeng,Zhao Junhua.A charging and discharging dispatching strategy for electric vehicles based on bi-level optimizaiton [J].Automation of Electric Power Systems,2012,36(11):30-37. [5] Kristien C,Edwin H,Johan D.The impact of charging plug-in hybrid electric vehicles on a residential distribution grid [J].Power Systems,IEEE Transactions on,2010,25 (1):371-380. [6] Tang X,Li J,Yu H.Charging Strategy Optimization for Plug-In Pure Electric Vehicle Based on Generalized Cost [C].America:ASCE,2013:2836-2841. [7] 王大勇,臧学运.公交区域车辆调度优化研究现状与发展[J].北京交通大学学报:自然科学版,2008,32 (3):42-45. Wang Dayong,Zang Xueyun.Reasearch on situation and developing trend for optimization theory and method of public transit vehicle scheduling problem [J].Journal of Beijing Jiaotong University,2008,32(3):42-45. [8] Andre P,Robin L.Optimal timetables for public transportation[J].Transportation Research Part B:Methodological,2001,35(8):789- 813. [9] Baita F,Pesenti R,Ukovich W.A comparison of different solution approaches to the vehicle scheduling problem in a practical case [J].Computers & Operations Research,2000,27(13):1249-1269. [10] Yan S,Chi C,Tang C.Inter-city bus routing and timetable setting under stochastic demands [J].Transportation Research Part A:Policy and Practice,2006,40 (7):572-586. [11] 李晋.基于时空网络的城市常规公交多车场车辆调度问题研究[D].北京:北京交通大学,2012. Li Jin.Research on Multiple Depot Vehicle Scheduling Problem of Urban Bus System Based on the Time-space Network[D].Beijing:Beijing Jiaotong University,2012. [12] Haghani A,Banihashemi M,Chiang K H.A comparative analysis of bus transit vehicle scheduling models [J].Transportation Research Part B:Methodological,2003,37(4):301-322. [13] Ali H,Qiang T,Hu H.Simulation model for real-time emergency vehicle dispatching and routing [J].Transportation Research Record:Journal of the Transportation Research Board,2004,1882(1):176- 183. [14] Avishai C.Public Transit Planning and Operation: Theory, Modelling and Practice[M].关伟,等译.北京:清华大学出版社,2010:128-130. Avishai C.Public Transit Planning and Operation: Theory, Modelling and Practice[M]. Guan Wei,et al,translate.Beijing:Tsinghua University Press,2010:128-130. [15] Wang H,Shen J.Heuristic approaches for solving transit vehicle scheduling problem with route and fueling time constraints [J].Applied Mathematics and Computation,2007,190(2):1237-1249. Dispatch Optimization of Pure Electric Buses Based on Charging Strategy Li Jun, Tang Xiaoyu, Zhao Changxiang (Research Center of Intelligent Transportation system, School of Engineering, Sun Yat-Sen University,Guangzhou 510006, Guangdong, China) An algorithm to optimize the fleet size of pure electric buses for single route and single charging station was proposed in consideration of charging range, charging rate, battery’s state of charge and dispatch strategy etc. The algorithm utilized a global optimization method to reduce the required number of electric buses and minimize the difference among bus departure frequency. A case study for Dongguan Songshan Lake bus line was presented to test the algorithm, and the bus schedule, charging rate, the influnce of bus power consumption, on running numbers of buses were analyzed. The proposed algorithm was compared with conventional buses dispatch algorithm. It is found that the proposed algorithm can effectively reduce the required number of buses and keep the balance of bus’ utilization rate, so that the cost of fleet operation can be optimized. vehicle engineering; pure electric bus; bus dispatch; state of charge; charging strategy; dynamic programming 10.3969/j.issn.1674-0696.2015.04.21 2014-03-20; 2014-06-18 国家自然科学基金项目(51178475) 李 军(1968—),男,湖北江陵人,副教授,博士,主要从事交通规划与政策方面的研究。E-mail:stslijun@mail.sysu.edu.cn。 U492.22 A 1674-0696(2015)04-107-06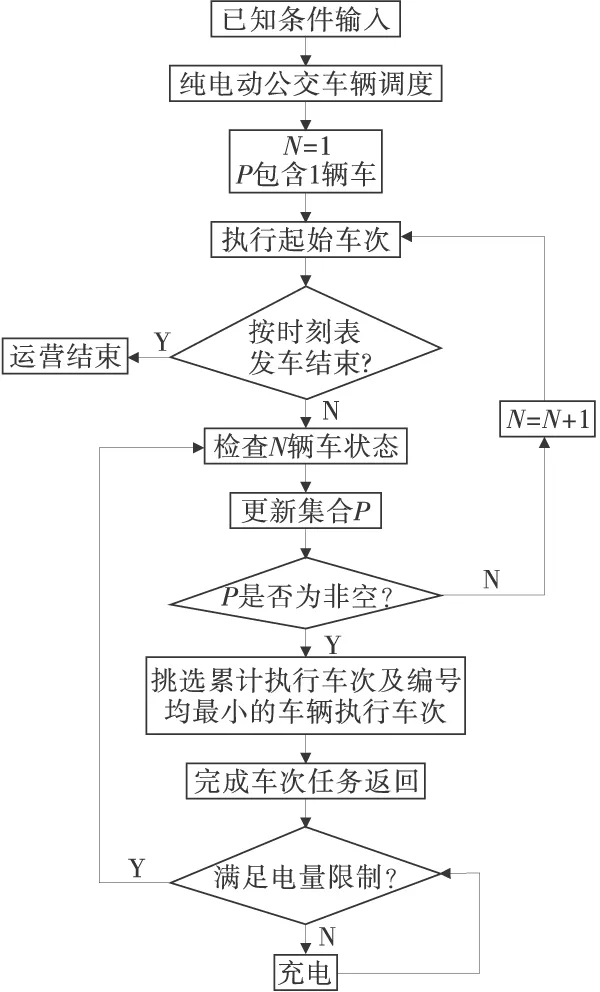
2 案例分析

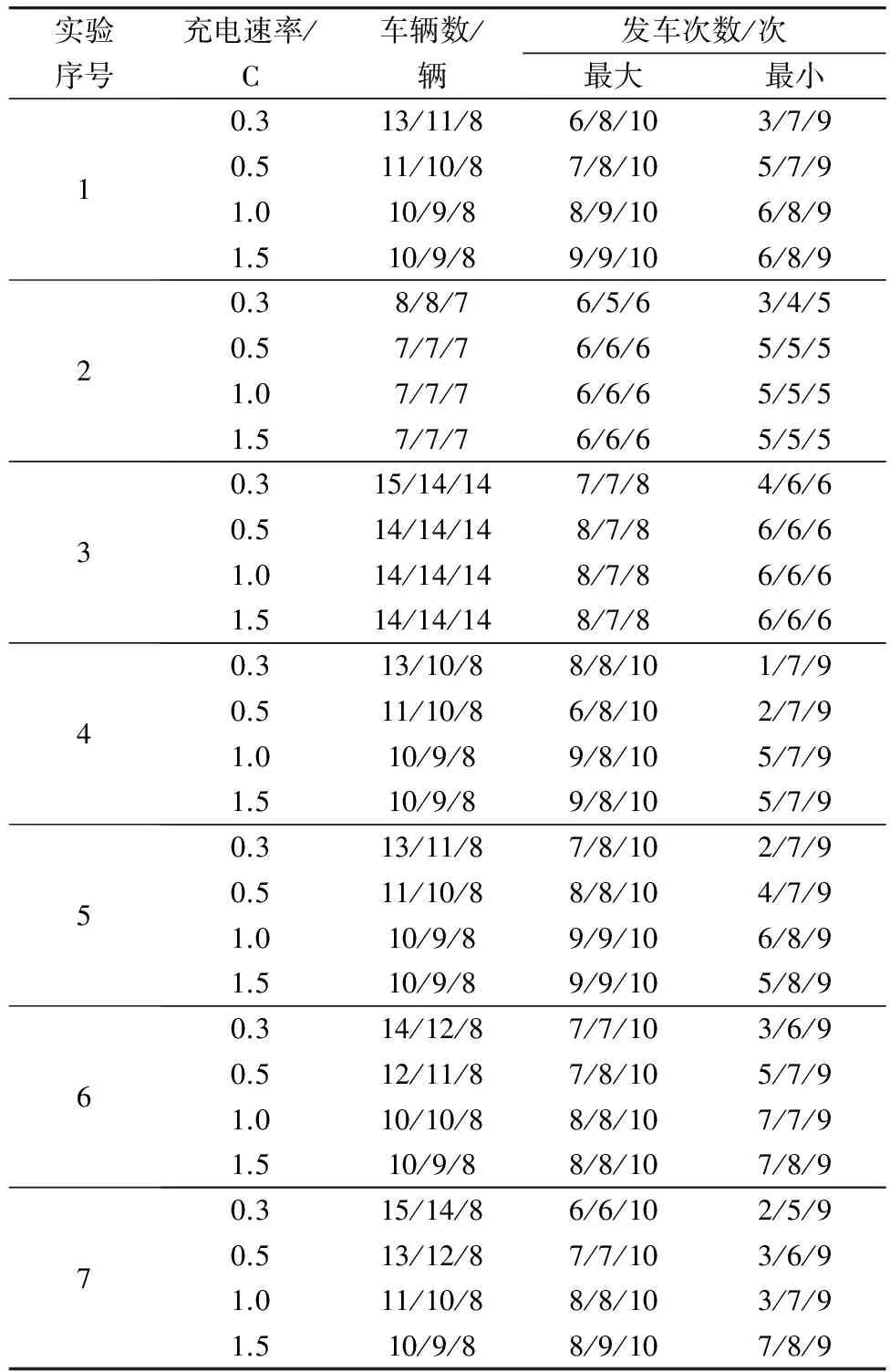
3 结 语
