一类Petri网可达标识数的有效计算方法

洪 良，周 健

（西安工程大学电子信息学院，陕西西安 710048）

一类Petri网可达标识数的有效计算方法

洪 良，周 健

（西安工程大学电子信息学院，陕西西安 710048）

S3PR网是Petri网的一个子类，基于组合学提出一种计算S3PR网可达标识数的代数方法.首先，通过组合学计算S3PR网可达标识数的上限.然后，基于资源回路理论，计算包含2个以及3个资源库所的信标，进而找到大部分甚至全部不可达标识的数量.最后，由可达标识数上限减去不可达标识，得到估算的可达标识数.该方法的性能通过例子计算与分析进行了验证.结果显示该方法可以在较短时间内计算出S3PR网的可达标识数，有助于可达图的生成.

柔性制造系统；Petri网；信标；可达标识

0 引 言

Petri网作为一种强有力的建模与分析工具，广泛地应用于资源分配系统中.在一个柔性制造系统中，原料通过不同的加工进程进入系统，并需求资源进行下一步的加工.事实上，一种资源往往被不同的加工进程所共用，由此形成的循环等待使系统陷入死锁状态.死锁问题是柔性制造系统中一个不可回避的问题.

人们基于Petri网研究了很多方法来处理柔性制造系统中的死锁问题［1－2］.文献［3］提出S3PR网是Petri网的一个子类，用于建模每一个工序只需要一种资源的生产系统；许可标识数是检验一个监督控制器的重要指标，文献［4－5］中基于信标的控制器设计方案计算复杂度低，但通常情况下得不到最优控制，也就是许可标识数最大；在离散事件系统的监督控制中，区域法成为一种重要的方法［6］；文献［7］通过对一个S3PR网进行区域分析，可以得到一个最大许可的监督控制器，但是，他们的方法需要可达图.计算可达图是一个极其耗费时间与资源的工作，当研究一个规模较大的网时，由于内存耗尽，研究者往往在计算机前守候数天、数周甚至数月却得不到任何结果［8］.

因此，在计算可达图之前，最好预先知道待计算网的可达标识数，然后基于当前的计算能力再判断能否得到结果或者权衡是否有进行计算的必要性.文献［9－11］基于组合学找出了部分S3PR网可达标识的数量，但他们的方法并不适用于所有的S3PR网.

文中的方法适用于所有S3PR网，可以在很短时间内估算出一个S3PR网的可达标识数，为可达图的计算提供帮助.

1 基本定义

Petri网是一个四元组，可表示为N＝（P，T，F，W）.其中，P代表库所的集合，用圆圈表示；T代表变迁的集合，用方框表示；F⊆（P×T）∪（T×P）称为流关系或者有向弧的集合；W：（P×T）∪（T×P）→N是一个映射，称为Petri网N的权函数，若f∈F，则W（f）＞0，若f∉F，则W（f）＝0.

N的P－向量I是映射：I：P→Z，P－向量是以P为序标的列向量，Z是整数的集合.P－向量I是Petri网N的P－不变式当且仅当I≠0，且IT［N］＝OT，其中［N］是一个以为序标的整数矩阵，称为关联矩阵.称P－不变式I是N的P－半流当且仅当I中的元素均为非负.‖I‖＝｛p｜I（p）≠0｝称为I的支撑.称P－不变式I是极小的若其支撑不是N的其他不变式支撑的严格超集，且其元素的最大公因子为1.

Petri网N＝（P，T，F，W）的标识M是一个从P到N的映射，（N，M0）称为网系统，M0称为N的初始标识.从M0可达的所有标识的集合称为（N，M0）的可达集，记为R（N，M0）.令X是一个矩阵，它的每一列都是N的一个P－半流，Ix（N，M0）＝｛M∈N｜p｜／XTM＝XTM0｝表示（N，M0）的不变式标识的集合.文中，标识跟不变式可以表示为多集形式.

S3PR网是Petri网的一个子类，其特点是每一个工序只需要一种资源的参与，一个资源不能连续参与两个工序的加工.由于S3PR网是普通网，一个S3PR网可表示为N＝（PA∪P0∪PR，T，F），其中PA代表工序库所的集合，P0代表闲置库所的集合，PR代表资源库所的集合.使用资源库所r的工序库所集合称为r的持有者.令S是N的严格极小信标，称为信标S的补集，其中，SR＝S∩PR.极小P－半流I称为极小资源P－半流或极小Pr－半流若其支撑仅包含一个资源库所r以及r的持有者，也就是说，‖I‖＝｛r｝∪H（r），此时I表示为Ir.

2 计算方法

2.1 可达标识数上限的计算

2.2 不可达标识的移除

3 算 例

如图1所示是一个典型的S3PR网.应用所提出的方法，通过计算此网的不变式标识数，可知此网包含7个Pr－半流，分别找到这7个Pr－半流导出的标识子网的不变式标识数，进而得到此网状态数的上限为675 000.可以找到4个包含2个资源库所的严格极小信标，并找到这4个严格极小信标对应的2－configuration，进而分别找到这4个2－configuration导出的此网的不可达标识数.这些不可达状态相加起来一共是54 000个.通过分析，可知其中有两对2－configuration是没有共享的资源库所的，重叠的个数一共是360个.这样得到计算的不可达状态数是53 640个.可以找到6个包含3个资源库所得严格极小信标，其中，只有一个信标中的资源库所不包含其他严格极小信标的资源库所，根据性质3，可以得到不可达状态为2 500个，重叠的个数一共是225个，最终的不可达状态数为2 275个.因此，总共的不可达状态数为55 915个.从此网的不变式标识数减掉不可达状态的数量最后得到，估算的此网的状态数一共是619 085个.而实际上，此网的可达状态数是600 424.因此，估算出来的结果跟实际结果是很接近的.

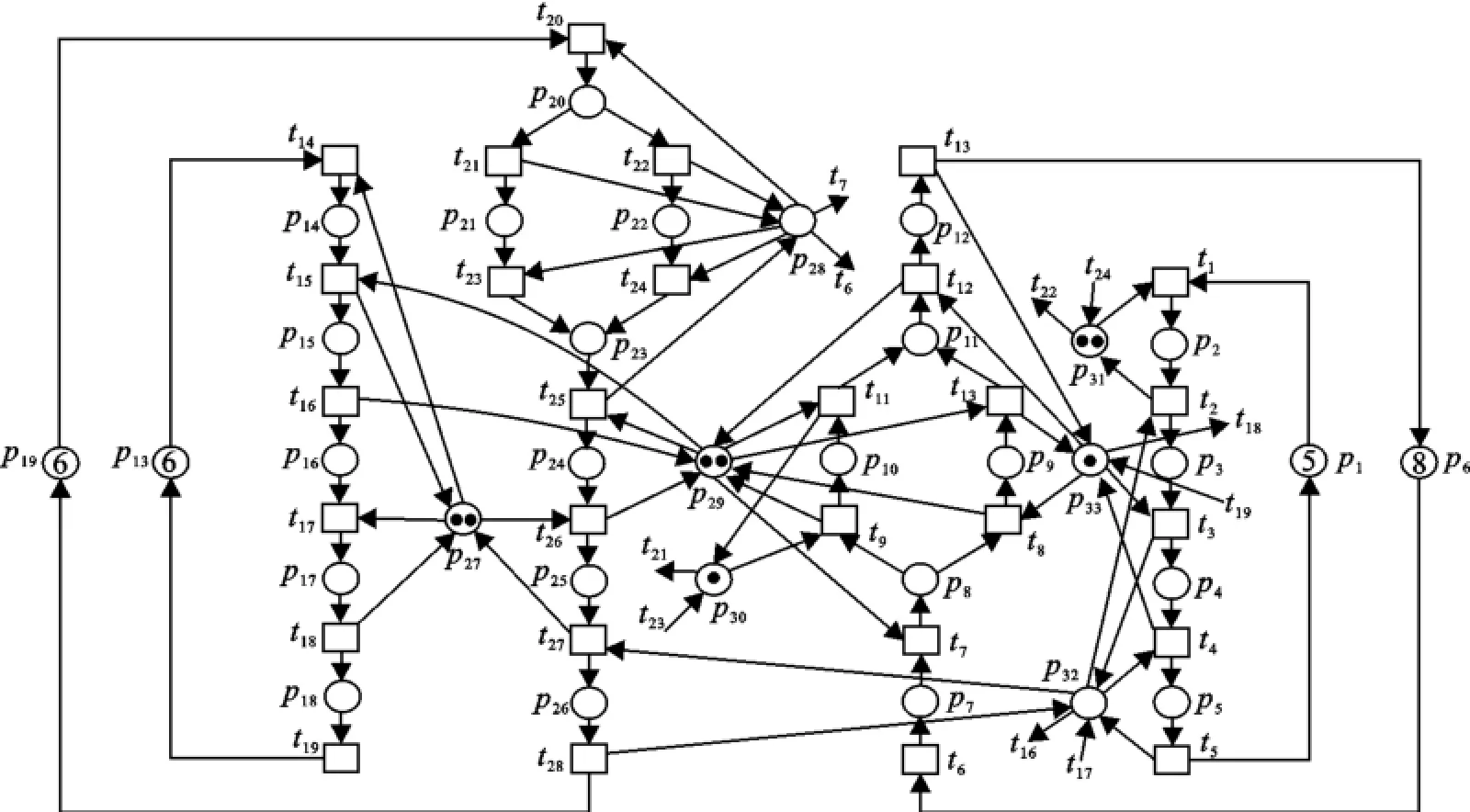
图1 S3PR网例子Fig.1 The S3PR example

表1显示了分别应用INA和文K方法于图1中的网，随初始标识改变，而求得的可达状态数与所耗费时间.其中，表格中“－”表示计算机内存耗尽，已无法计算出可达状态.从表1中可以看出，此网的可达状态随初始标识的增大而迅速增加.应用INA求得状态所需的时间也是迅速增加，甚至在标识5下已无法找到最终的可达图.而结果显示，应用文中方法，计算时间对初始标识的改变并不敏感，而是基本保持恒定，图2清晰地显示了这一点.因为INA的计算可达状态的能力是有一个上限的，通过结果分析，知道可以通过应用此文方法来估计一个S3PR网的可达状态数，来判定是否有必要通过INA来计算此网的可达图.

通过INA可以计算一个网的可达图.一个网的可达图规模跟网的节点数和初始标识的大小成指数关系.可见，INA的计算能力对初始标识的大小敏感.接下来，通过调整图1中S3PR网的初始标识来检验此文方法对一个网初始标识的敏感性.以下的计算是在Windows XP操作系统下，用Pentium（R）Dual－Core CPU 2.6GHz，内存为3G的计算机下进行的.随着图1中网初始标识的改变，分别应用INA和此文方法来计算可达状态数.

表1 INA与本文方法性能对比Table 1 Comparison between INA and the proposed method

4 结束语

基于组合学，给出一种估算S3PR网可达标识数的方法.首先，计算网的可达标识数上限.然后，通过含有2个资源库所的信标确定不可达标识数.两者的差值即为所求的结果.由于引入了组合学，此方法具有相当低的计算复杂度，可以作为计算可达图的前期工作.

［1］ LI Z W，ZHOU M C.Elementary siphons of Petri nets and their application to deadlock prevention in flexible manufacturing systems［J］.IEEE Trans on Systems，Man and Cybernetics，Part A，2004，34（1）：38－51.

［2］ LI Z W，ZHOU M C.Two－stage method for synthesizing liveness－enforcing supervisors for flexible manufacturing systems using Petri nets［J］.IEEE Trans on Industrial Informatics，2006，2（4）：313－325.

［3］ EZPELETA J，COLOM J M，MARTINEZ J.A Petri net based deadlock prevention policy for flexible manufacturing systems［J］.IEEE Trans on Robotics and Automation，1995，11（2）：173－184.

［4］ WANG S G，WANG C Y，ZHOU M C，et al.A method to compute strict minimal siphons in S3PR based on loop resource subsets［J］.IEEE Trans on Systems，Man and Cybernetics，Part A，2012，42（1）：226－237.

［5］ WANG S G，WANG C Y，ZHOU M C.Controllability conditions of resultant siphons in a class of Petri nets［J］.IEEE Transactions on Systems Man ＆Cybernetics，Part A，2012，42（5）：1206－1215.

［6］ GHAFFARI A，REZG N，XIE X L.Design of a live and maximally permissive Petri net controller using the theory of regions［J］.IEEE Transactions on Robotics and Automation，2003，19（1）：137－142.

［7］ UZAM M，ZHOU M C.An iterative synthesis approach to Petri net－based deadlock prevention policy for flexible manufacturing systems［J］.IEEE Transactions on Systems Man ＆Cybernetics，Part A，2007，37（3）：362－371.

［8］ HONG L，CHAO D Y.Enumeration of reachable states for arbitrary marked graphs［J］.IET Control Theory and Applications，2012，6（10）：1536－1543.

［9］ CHAO D Y，YU T H.Enumeration of reachable（forbidden，live，and deadlock）states of top k－th order system（with a non－sharing resource place）of Petri nets［C］／／Industrial Electronics Society，IECON 2013－39th Annual Conference of the IEEE.Vienna：IEEE，2013：3517－3523.

［10］ CHAO D Y，YU T H，WU S C.Closed form formula construction to enumerate control related states of K－th order S3PR system（with a Top Left side non－sharing resource place）of Petri nets［C］／／Networking，Sensing and Control（ICNSC），2014IEEE 11th International Conference on.Miami：IEEE，2014：132－137.

［11］ CHAO D Y，YU T H，CHEN T Y.Computation of control related states of middle k－th order system（with a nonsharing resource place）of Petri nets［C］／／Computer，Consumer and Control（IS3C），2014International Symposium on.Washington：IEEE，2014：244－247.

［12］ ROBERTS F S，TESMAN B.Applied combinatorics［M］.Oxford：Taylor ＆Francis，2009.

编辑、校对：孟 超

Effective enumeration of reachable markings for a class of Petri Nets

HONG Liang，ZHOU Jian
（School of Electronics and Information，Xi′an Polytechnic University，Xi′an 710048，China）

An S3PR is a class of Petri Nets.This work proposes a combinatorics based method that deals with an approximate calculation of the number of reachable markings of an S3PR in an algebraic way.First，an upper bound of reachable markings of an S3PR can be found by combinatorics.Second，the number of most even all unreachable markings can be obtained by extracting siphons with two and three resource places from resource circuits.Finally，the number of reachable markings can be estimated by removing the unreachable ones from the upper bound.Example calculations and analyses show the performance of the proposed method.The result shows that the number of reachable markings of an S3PR can be calculated by the proposed method in a short period of time，which contributes to the generation of reachability graphs.

flexible manufacturing system；Petri Net；siphon；reachable markings

TP 13

A

1674－649X（2015）05－0606－05

10.13338／j.issn.1674－649x.2015.05.016

2015－06－10

陕西省自然科学基础研究计划资助项目（2015JQ6258）

洪良（1984—），男，河北省唐山市人，西安工程大学讲师，研究方向为自动控制理论、Petri理论及应用.E－mail：hongliang20030605＠163.com