高频信号扩展卡尔曼滤波器设计

谷善茂，刘云龙，张 妮，杜 德

(潍坊学院信息与控制工程学院，山东潍坊)



高频信号扩展卡尔曼滤波器设计

谷善茂，刘云龙，张 妮，杜 德

(潍坊学院信息与控制工程学院，山东潍坊)

为了实现永磁同步电动机转子位置估计试验的高频信号滤波，基于扩展卡尔曼滤波器原理，提出了一种改进的基于FPGA的信号提取方案，设计了高频信号扩展卡尔曼滤波器。该滤波器采用迭代算法提取转子位置信息，并对基频控制电流进行滤波处理，比传统IIR滤波器或FIR滤波器具有更快的滤波速度和更好的滤波性能。该滤波器简单易实现，消除了反馈回路中的低通滤波器。由于反馈回路中没有高频信号成分的干扰，控制器对高频位置估计的影响较小，所设计的位置估计器几乎不受控制器的影响，简化了位置估计器的设计。最后，仿真结果说明文中方法的可行性，并给出了一个基于EKF的低速无传感器试验。

永磁同步电动机；无传感器；高频信号注入；扩展卡尔曼滤波器；迭代算法；位置估计

0 引言

高频信号注入方法对于永磁同步电动机(permanent magnet synchronous motor,PMSM)在低速甚至零速情况下的转子磁极位置估计，非常有效可靠。文献[1]提出了一种脉振高频信号注入方法，在低速情形下，能够获得良好的位置、速度估计，但动态性能欠佳。针对位置估计时收敛方向不确定的问题，文献[2-3]基于旋转高频法给出了磁极极性的判定方法。文献[4]从电机磁场饱和的角度出发，对电机电感与转子位置之间的关系进行了阐述，但最多只能估计出转子位置的6个区间。文献[5]根据高频信号注入时转子脉动信号，给出了适用于初始位置检测的位置信号估计。龙贝格磁链观测器[6]、反电动势方法[7]、状态方程磁链估计[8]等方法实现了电机在中、高速的位置估计，但不适用零速、极低速情况。目前，能够较好实现零速、极低速情况下的无传感器控制方法是高频信号注入法，但其信号的提取方法非常复杂，多重滤波器不仅导致提取的位置信号有时延和相移，而且反馈回路加入低通滤波器后使得系统的动态性能降低。卡尔曼滤波器是一种高效可靠的递归型滤波器，能够从一系列的不完全及包含噪声的量测信息中，估计出动态系统的状态变化[9]。

本文基于扩展卡尔曼滤波器原理，提出了一种改进的基于FPGA的信号提取方案，设计了一种改进的高频信号扩展卡尔曼滤波器(extended Kalman filter,EKF)。该滤波器采用迭代算法提取转子位置信息，并对基频控制电流进行滤波处理。该滤波器设计简单易实现，消除了反馈回路中的低通滤波器，提高了系统的稳定性和动态性能。

1 高频信号滤波的实现原理

图1 高频信号注入实现的基本原理图

多个同步轴系滤波器的使用，不仅造成估计出来的位置信号有时延和相移，而且滤波器的计算复杂，在信号处理器上难以实现[11]。反馈控制回路中的低通滤波器的引入，会造成系统的动态性能下降，严重时甚至不稳定。但是如果去除反馈回路的低通滤波器，电流中的高频成分经过电流调节器的放大作用又会形成相位滞后于注入电压π/2角度的干扰量。

2 高频信号EKF设计算法

当高频旋转电压信号注入时，经过凸极调制的电流为

iαβi=idqiejθr=Ii_1pej(ωit-π/2)+Ii_1nej(-ωit+2θr+π/2)

(1)

上式改写为方程形式

iαi=Ii_1pcos(ωit-π/2)+Ii_1ncos(-ωit+2θr+π/2)

(2)

iβi=Ii_1psin(ωit-π/2)+Ii_1nsin(-ωit+2θr+π/2)

(3)

对上式进行三角函数展开并整理：

iαi=A1sin(ωit)+B1cos(ωit)

(4)

iβi=A2cos(ωit)+B2sin(ωit)

(5)

式中：

A1=Ii_1p+Ii_1ncos(2θr)

(6)

A2=-Ii_1p+Ii_1ncos(2θr)

(7)

B1=-Ii_1nsin(2θr)

(8)

B2=Ii_1nsin(2θr)

(9)

由式(6)～式(9)可得：

(10)

(11)

由式(10)、式(11)知，基于锁相环原理运算可得到电机的转子位置角，其实现过程如图2所示。

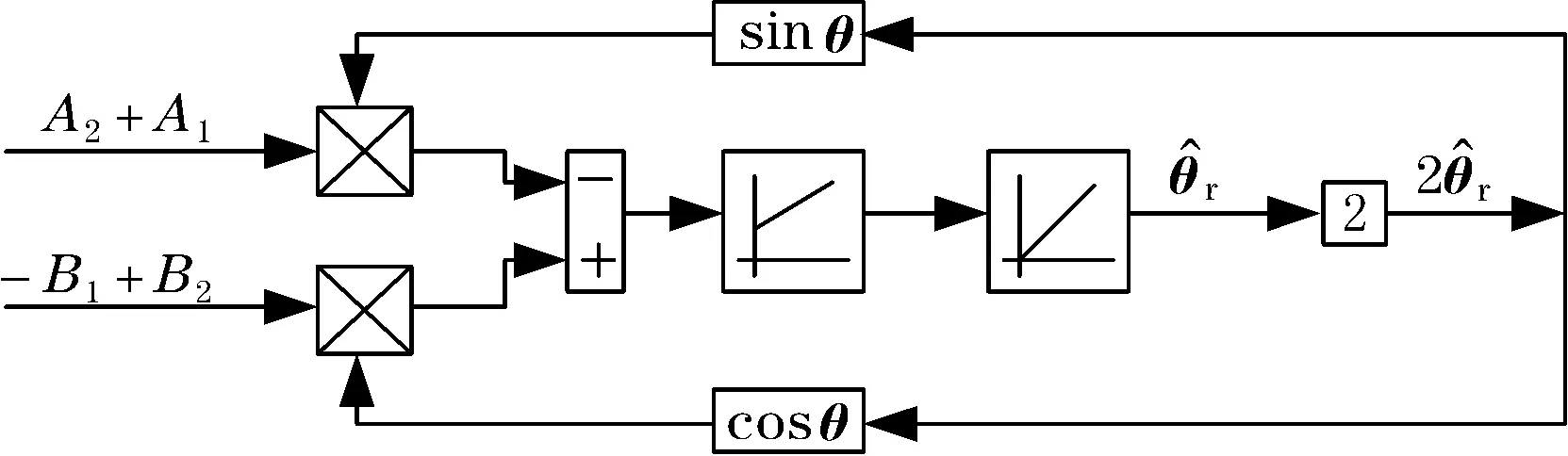
图2 锁相环实现的过程图

假定电机的采样频率远大于电机的电角频率，以实测电流量值作为所设计的EKF的输入变量，则电流基波分量在2次的采样间隔可近似为常值。在两相静止坐标系上，叠加高频电压信号后产生的高频电流信号如下：

iα=Α1sin(ωit)+B1cos(ωit)+ifα

(12)

iβ=Α2cos(ωit)+B2sin(ωit)+ifβ

(13)

式中：ifα为基波电流在α轴的分量；

ifβ为基波电流在β轴的分量。ifα、ifβi在相邻两个采样周期内可认为是一常数。为了减少量化误差，提高滤波器的精度，将基波电流部分削弱后再送入滤波器进行滤波处理，具体实现过程为：首先将实测电流量值转换到两相静止坐标系中，经低通滤波去除高频成分后，作为基波电流的参考值；然后从电流实测值中减去参考值，则上述方程可描述为

(14)

(15)

式中：dα为基波电流的α轴的误差分量；dβ为基波电流的β轴的误差分量。

取式(14)、式(15)中电流参量sin(ωit)、cos(ωit)的幅值及基波电流误差分量dα、dβ作为扩展卡尔曼滤波的状态变量，则有

xα=[A1B1dα]T

(16)

xβ=[A2B2dβ]T

(17)

状态变量A1、A2、B1和B2中均包括了两倍转子位置角有关的三角函数，当采样频率远大于电机的基波角频率时，上述状态变量是缓慢变化的；同时考虑噪声及外部干扰的影响，电流的离散状态方程如下[11]：

xk+1=xk+wk=Fxk+wk

(18)

yk=Cxk+vk=[cos(ωit) sin(ωit) 1]xk+vk

(19)

式中：F为3阶单位矩阵；w为误差噪声；v为测量及采样误差噪声。

定义误差协方差矩阵如下：

(20)

从而得到基于扩展卡尔曼滤波原理的电流滤波实现过程如下：

(1)预估

(21)

(22)

(2) 增益矩阵计算：

(23)

式中：

Cα=[sin(ωit) cos(ωit) 1]T

(24)

Cβ=[cos(ωit) sin(ωit) 1]T

(25)

(3) 状态更新

(26)

Pk+1|k+1=[F-Kk+1C]Pk+1|k

(27)

式中：Ts为系统采样时间；Qk为协方差矩阵；Rk为对角矩阵；Pk为对称矩阵。

滤波器在α、β轴上的输出分别为：

(28)

(29)

式中的基波电流估计值为其误差部分，总的基波电流估计值应为：

(30)

(31)

将估计电流变换到转子旋转坐标系上，以交轴、直轴电流作为电流调节器的反馈输入。滤波所得的高频幅值部分首先经过外差运算，然后利用锁相环原理来实现转子位置的估计，其外差处理过程如下：

(32)

将式(6)～式(9)代入式(32)，化简得：

(33)

(34)

式中给出的位置误差信号可以作为锁相环的输入来进行转子位置、速度的估计，其计算过程有

(35)

(36)

3 仿真研究

在Matlab/Simulink工具箱中建立EKF仿真模型，在两相静止坐标系下，定子电流和高频旋转三角函数值为系统输入，高频电流幅值的辨识值及基波电流误差分量为系统输出，滤波所得的高频电流幅值部分送入锁相环观测器为电机转子位置信息。电机参数如表1 所示，仿真步长为10-6，EKF的采样周期为10-5，噪声协方差矩阵及误差估计矩阵、的取值如下：

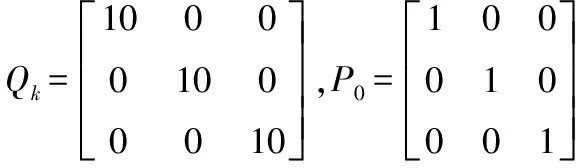
x0=[0 0 0]T，Rk=[1]

表1 电机参数

考虑注入高频信号的电压幅值为15 V，频率500 Hz，比较EKF与四阶巴特沃斯带通滤波器的高频电流。给定转速0 r/min，转矩为0时，α轴上高频电流仿真结果如图3所示(β轴上的高频电流仿真结果与α轴相似，图中EKF代表扩展卡尔曼滤波方法结果，BPF代表四阶巴特沃斯带通滤波方法结果)。从仿真可以看出，当速度为零时，改进的EKF高频电流值很快达到了稳定，比带通滤滤波器具有更快的反应速度。

图3 零速、空载时α轴高频电流波形

如果转速不为0，给定转速60 r/min(2 Hz)，转矩给定1 N·m时，EKF和四阶巴特沃斯带通滤波器的在α轴上的高频电流仿真结果和β轴上的高频电流仿真结果相似。这里只给出α轴的仿真结果，如图4所示。

图4 给定转速60RPM，负载1 N·m时α轴高频电流波形

图5是EKF和二阶巴特沃斯低通滤波器(通带截止频率为250Hz)的基频电流波形，转速从零到60 r/min(2 Hz)，转矩给定在0.07 s时阶跃变化到1 N·m时，α、β轴上的基频电流仿真结果(图中Mea代表实际测量结果)。从仿真中可以看出，无论速度是否为零、带载还是空载，EKF基波电流值很快达到了稳定，与巴特沃斯低通滤波器相比，具有更小的时延，没有相位滞后，且滤波效果更好，这些都有助于提高系统的动态性能。

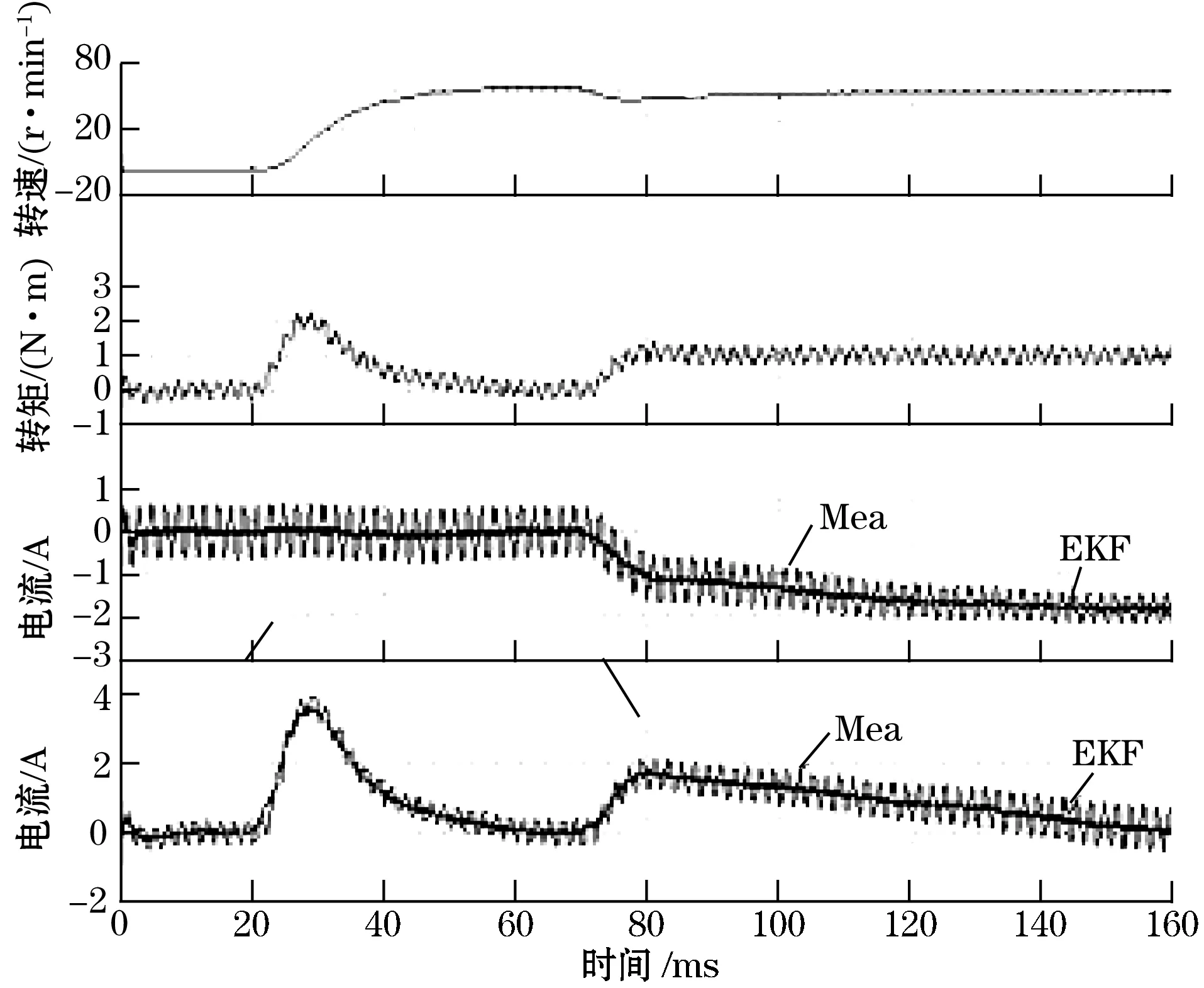
图5 EKF与二阶巴特沃斯低通滤波器的基频电流波形

考虑给定初始速度为零，在0.02 s阶跃变化到60 r/min；给定初始转矩为0，在0.07 s阶跃变化到1 N·m时，EKF和传统外差与带通滤波器的转子位置仿真估计波形如图6所示(图中HF代表传统滤波方法所得结果)。从仿真中可以看出，EKF滤波方法的位置估计信号比基于带通滤波器的位置估计信号误差小的多，且跟踪速度更快，这是因为带通滤波使得电流信号的相位发生了变化，反映到位置估计中就会有恒定的位置偏差。

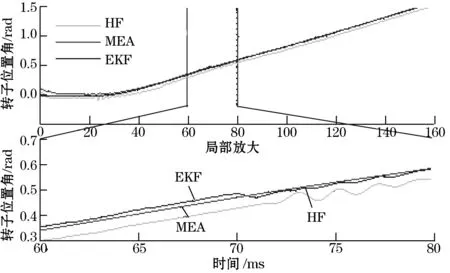
图6 转子位置估计仿真波形

在速度给定突然变化时，图3～图6中的各分量出现了短暂的波动，但调节过程时间很短，之后快速恢复到稳态。由此可见，即使在系统的暂态过程中，EKF也能够较好的实现高频分量和基频分量的分离，具有很强的鲁棒性，对系统控制环节参量的变化具有较强的抑制效果，可以在比较恶劣的工况下实现很好的滤波。

本文给出的EKF设计具有以下优点：

(1)采用迭代算法，其滤波时延和相称都非常小，提高了系统的稳定性和动态性能；

(2)高频信号与基频信号实现了良好的分离，使得位置观测器的设计与系统的调节器参数无关，降低了位置观测器的设计难度；

(3)包含位置信息的负相序幅值信号分离速度较传统滤波快，提高了位置误差信号的提取速度。

4 基于EKF的PMSM低速无传感器试验

基于EKF的PMSM低速无位置传感器实验系统是基于高频信号注入的位置估计，采用EKF提取高频信号。考虑EKF计算速度要求较快，通过仿真分析发现，只有当仿真的步长小于10-5s时，才能实现较好的滤波效果，需采用FPGA来实现，这主要是滤波后所得的高频信号幅值部分再经过简单的锁相环运算，就得到了转子位置信号；将这个位置信号通过信号采集电路输入到dSPACE1103控制系统，可实现永磁同步电动机的无位置传感器控制。

将Matlab/Simulink工具箱硬件协仿真生成的FPGA的EKF模型通过ISE SystemGenerator10.1生成HDL语言，将HDL语言下载到Virtex VII Pro FPGA开发板的配置Flash中，相应的接口及AD、DA控制程序用有限状态机实现[12]；图7和图8分别为转速为2π rad/s和4 π rad/s时的估计位置与实测位置及测量的高频电流波形。

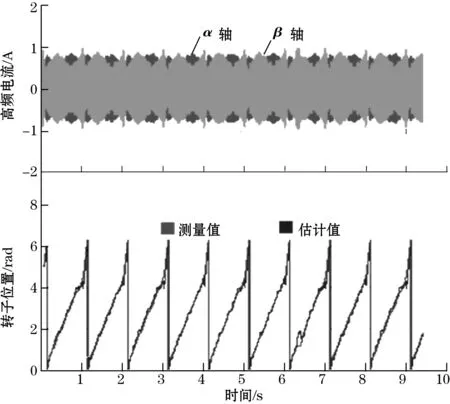
图7 ωr=2π rad/s高频电流及估计位置波形

图8 ωr=4π rad/s高频电流波形及估计的转子位置

从上述波形试验可以看出，EKF实现了很好的滤波效果，位置估计信号跟踪很快，高频信号经过EKF之后，获得了良好的位置跟踪能力，在2 π rad/s的低速时，系统仍然可以实现较好的位置跟踪，且位置跟踪较快。无论电机位置波动如何，该方法都可以实现快速的位置跟踪。

5 结论

针对高频信号注入时的电流信号，提出了一种改进的基于扩展卡尔曼滤波原理的高频信号处理方法。该方法同时实现高频信号和基波信号的滤波分离处理，使得了位置估计器的设计与系统电流调节器参数无关，简化了位置估计器参数的设计。该信号处理方式不需要额外的IIR滤波器或FIR滤波器，信号处理速度较传统滤波方法快，实现了基频信号的提取，提高了系统的稳定性和动态性能。

[1] CHEN J L,TSENG S K,LIU T H.Implementation of high performance sensorless interior permanent magnet synchronous motor control system using a high-frequency injection technique.IET Electric Power Applications,2012,6(8):533-544.

[2] 于艳君,柴凤,欧景,等.基于旋转高频信号法的无位置传感器控制.电工技术学报,2013,28(7):26-31

[3] 刘颖,周波,冯瑛,等.永磁同步电机低速无传感器控制及位置估计误差补偿.电工技术学报,2012,27(11):38-45

[4] QIU X,HUANG W,BU F.Virtual Hall method for sensorless control of IPMSMs using high-frequency signal injection.Electronics Letters,2013,49(17):1092-1097.

[5] 李毅拓,陆海峰,瞿文龙,等.一种新颖的永磁同步电机转子初始位置检测方法.中国电机工程学报,2013,33(3): 75-82.

[6] 张磊,高春侠.改进型永磁同步电机全速度范围无传感器控制策略.电机与控制学报,2012,16(7):103-110.

[7] LU A,HAMEYER K.A comparative study of sensorless speed control.International Journal of Applied Electromagnetics and Mechanics,2012,39(7):787-791.

[8] GABRIELA,CRACIUNAC.dynamic performances in sensorless system with Two-Phase Induction Motor.Journal of Electric and Electronics Engineering,2013,6(2):9-12.

[9] 赵锦剑,杨光永,周安然,等.旋转机械振动信号的 Kalman 滤波及故障诊断.仪表技术与传感器,2014 (5):80-83.

[10] 谷善茂,何凤有,谭国俊,等.永磁同步电动机无传感器控制技术现状与发展.电工技术学报,2009,24(11):14-20.

[11] 谷善茂.永磁同步电动机无传感器控制关键技术研究:[学位论文].徐州：中国矿业大学，2009.

[12] 徐文波,田耘.Xilinx FPGA开发实用教程.北京：人民邮电出版社,2013.

Design of High Frequency Signal Extended Kalman Filter

GU Shan-mao,LIU Yun-long,ZHANG Ni,DU De

(College of Information and Control,Weifang University,Weifang 261061,China)

In order to achieve high frequency signal filtering on permanent magnet synchronous motor (PMSM) position estimation experiment,a modified signal extraction method based on FPGA was presented,and an extended Kalman filter (EKF) was designed.The filter can not only extract rotor position information,but also filter fundamental frequency control current based on iterative algorithm.Compared with traditional IIR filter or FIR filter,the EKF has faster filter speed,and better filter performance.It was designed easily,and eliminated low-pass filter in control feedback loop.At the same time,since there was no high frequency signal component in control circuit,the controller affection to high frequency position estimation was decreased.The design of position estimator was unaffected by control,and simplified.Finally,simulation result was adopted to verify the validity of the proposed method,and a low speed sensorless experiment test was given based on EKF method.

permanent magnet synchronous motor; sensorless; high frequency signal injection; extended Kalman filter; iterative algorithm; position estimation

山东省自然科学基金项目(ZR2012FL06)；山东省高校科技计划项目(J13LN81)； 潍坊学院博士基金项目(2013BS10)

2014-07-12 收修改稿日期：2015-02-20

TM351

A

1002-1841(2015)07-0090-04

谷善茂(1978— )，讲师，博士，主要研究领域为永磁同步电动机无传感器控制，电力电子驱动控制与检测技术。E-mail：gsm197851@126.com.