电力系统机电振荡的非线性现象分析

马 列，张 瑛，于 瑶，龚 娜，孙立谦

（1.沈阳工程学院，辽宁 沈阳 110136；2.南京南瑞继保电气有限公司，江苏 南京 211111）

电力系统机电振荡的非线性现象分析

马 列1，张 瑛1，于 瑶1，龚 娜1，孙立谦2

（1.沈阳工程学院，辽宁 沈阳 110136；2.南京南瑞继保电气有限公司，江苏 南京 211111）

电力系统机电振荡现象是伴随系统网络规模的扩大而产生的，研究机电振荡现象对于分析区域电网的安全稳定具有重要意义。以往的分析手段多采用线性化的分析方法，而电力系统本身是一个非线性系统，系统的非线性特性必然对机电振荡的响应产生影响。为此，采用非线性模型获得系统在机电振荡情况下的响应轨迹，分析系统非线性程度不同时对响应曲线在幅值和周期上发生的变化。这些分析对于电力系统机电振荡现象的理解和认识具有一定的参考意义。

机电振荡；非线性；时域仿真；强迫功率振荡

电力系统是一个非线性系统，随着我国华北、华东、华中电网的互联互通，由于系统规模扩大所导致的电力系统机电振荡问题已经直接威胁到电力系统的安全稳定运行［1］。

分析电力系统机电振荡问题的传统方法多采用线性化分析，即将全系统的动态微分方程在系统平衡点处线性化，形成状态方程。根据线性系统的理论，系统的小干扰稳定性与状态方程的特征值和特征向量密切相关，通过特征值的分布和性质，可确定系统的振荡模式。通过分析，可判断系统机电振荡回路中区间振荡模式和局部振荡模式的关系，系统阻尼变化等一系列信息。该方法是分析电力系统机电振荡最有效的方法之一。

然而当电力系统表现为较强的非线性特性时，如系统网络规模庞大或输电线路承载较大负荷等，系统在发生机电振荡时表现出复杂的动态特性，用线性化方法难以分析。因而，有必要在系统机电振荡分析中考虑非线性因素对系统稳定的影响。

目前，研究人员已经对电力系统的非线性影响与系统稳定性问题进行了一系列研究和分析。文献［2］采用Carleman线性化方法获得系统的非线性高阶模态，将线性模态参与因子的概念扩展到非线性模态中，定量衡量各振荡模式之间的非线性相关作用。文献［3］分析比较了电力系统两种主要的非线性分析方法（即模态级数法和正规形方法）对时域仿真解的逼近程度。结果显示，随着系统非线性强度的增加，模态级数法的误差及其增加速度最小。文献［4］研究了基于希尔伯特—黄变换法从广域测量系统的实测数据中提取电力系统时变振荡特性的一种实用方法。该方法能够分析非线性、非平稳信号的局域动态行为和特性，更好地反映振荡过程中所包含的多个模式随时间变化的规律及模式间的相互影响，从而提高识别能力和处理效果。

本文利用时域仿真方法获得模型系统的机电振荡响应轨迹，分析系统在不同扰动量时的轨迹非线性响应特征，针对扰动量为6个周波时间的响应轨迹的幅值和频率进行分析，指出电力系统机电振荡过程中的非线性特性导致轨迹在幅值和周期上发生的变化。仿真无穷大系统发生周期性的小扰动，模拟机电振荡中的强迫振荡发生条件，试验中产生较大幅值的强迫功率振荡。试验证明，系统周期性的小扰动是导致机电振荡的原因，并在扰动频率和发电机组固有振荡频率接近时，系统达到最大振幅。

此研究有利于了解机电振荡后的系统响应现象，为抑制机电振荡及研制电力系统稳定与控制器提供一定的参考。

1 不同扰动条件下系统响应的变化

系统机电振荡过程中，发电机的转速、频率和输出电磁功率均发生明显变化。为分析非线性因素对系统机电振荡的影响，本文通过基于系统轨迹辨识技术的时域仿真法，仿真输电线路上发生机电振荡现场，分析机电振荡过程中非线性因素对响应轨迹形态的影响。

为获得系统机电振荡后的响应轨迹，本文利用Matlab软件中Simulink仿真环境，搭建无穷大系统。在Simulik仿真环境中构建的仿真模型如图1所示。

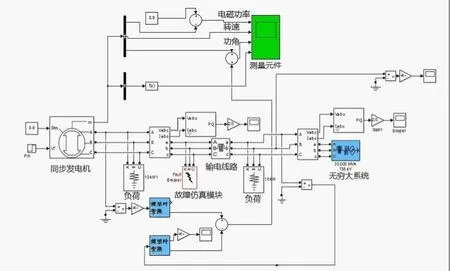
图1 Simulink仿真环境中所搭建的单机无穷大模型

在该仿真系统中，通过对发电机机端施加三相短路故障，观察系统在不同扰动量条件下，其功角δ、转速ω、输出电磁功率Pc的响应曲线。扰动量的大小通过改变故障元件的故障持续时间来实现。图2是扰动量为3个周波时间时系统的功角响应曲线。

分析图2可知，当发电机机端发生三相短路时，发电机功角δ在幅值上有较大突变。在系统阻尼作用下，幅值逐渐减小，系统趋近于稳定运行状态。通过观察发电机的转速ω和输出功率Pe的变化曲线，可得出相同结论。

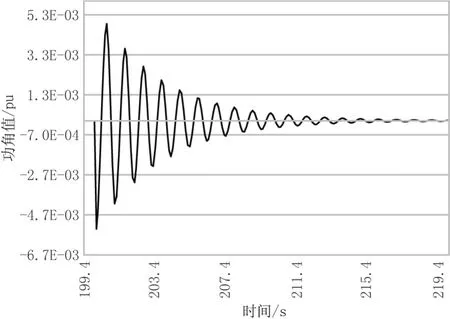
图2 扰动量为3个周波时间的发电机功角响应曲线

不同扰动量条件下，发电机功角机电振荡响应曲线的初始振荡幅值、周期、频率如表1所示。

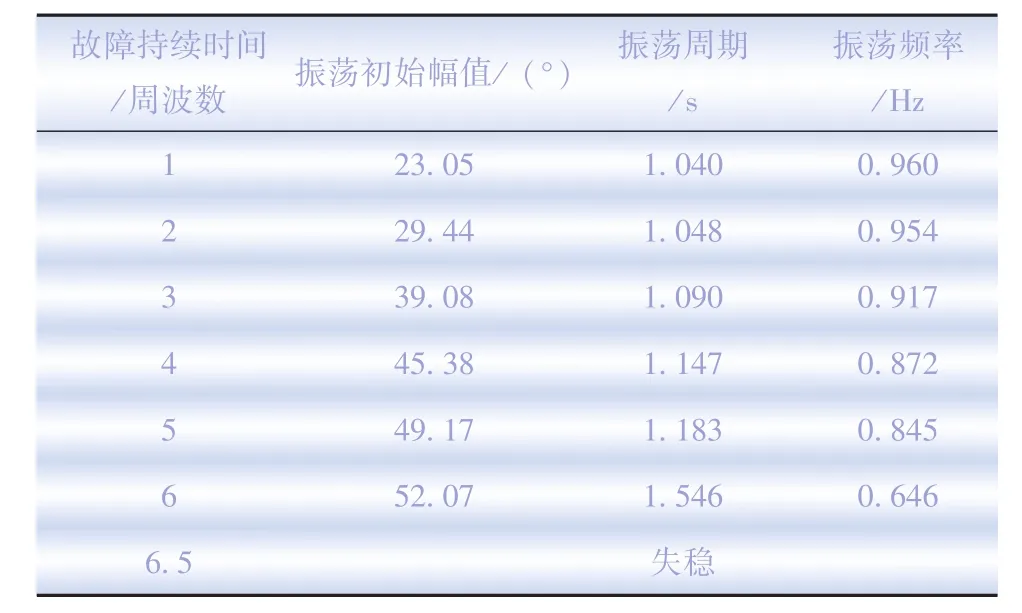
表1 不同扰动量条件下的功角振荡幅值、周期和频率

系统改变扰动量时，随着扰动量的不断加大，系统所遭受的冲击也在加大，非线性动态电力系统的初始运行点逐渐远离系统的稳定运行点，系统故障响应曲线的初始峰值增大，振荡周期变长，振荡频率降低。

当电力系统的规模越大，区域联络线上潮流越重，系统运行状态越远离稳定运行点，非线性程度就越强。一旦发生机电振荡，系统的频率就会变低，甚至出现低至0.1 Hz的振荡现象。

当扰动量增大到一定程度时，可能超出系统的稳定运行域，导致系统失稳。通过仿真发现当扰动量为6.5个周波时间时，系统失去稳定。结果如图3所示。

2 同一扰动条件下机电振荡响应的变化

研究机电振荡过程中的发电机功角δ、转速ω、输出电磁功率Ρe的振荡周期和振荡频率的变化有利于我们认识机电振荡现象，为研制相关机电振荡抑制器提供一定的理论依据。

上述单机无穷大模型仿真系统中，扰动量为6.5个周波时间系统发生失稳。当扰动量为6个周波时间时，此时系统的初始振幅最大，系统非线性特性对响应曲线的影响作用达到稳定域内的最大值。

2.3.3 试验过程 参照 《中国药典》2015年版二部奥美拉唑肠溶胶囊溶出度检测方法[4]，研究A、B、C、D和E经pH 1.2盐酸溶液120 min后，在pH 6.8、pH 6.0、pH 5.5和水介质中的溶出实验条件，见表3。

图3 扰动量增大到一定程度时系统失稳

设置扰动量为6个周波时间，记录功角δ、转速ω和电磁功率Pe在故障发生后的第1～6周期的振荡周期变化。结果如表2所示。

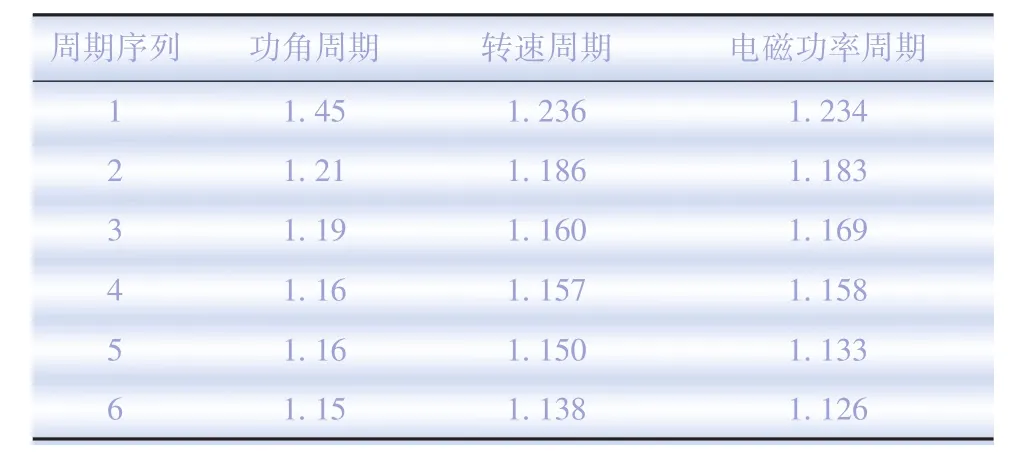
表2 同一扰动量下的振荡周期变化s

对表2中数据进行分析可知，在系统遭受一定量的扰动时，由于系统存在正阻尼，随着时间的增加，阻尼使系统振荡的能量不断减少，最终导致振荡幅值减小。同时，因系统非线性特性因素的影响，在系统初始振荡周期达到发生短路故障最大值时，系统功角、转速和电磁功率的振荡周期随时间变化呈减少趋势。

在仿真模型中，当设置扰动量小于6个周波的其他时间时，可得到相同结论。

采用各种基于轨迹辨识的分析方法和非线性理论方法，如Prony分析方法［5］、分岔理论［6］、正规形方法［7］、混沌理论［8－9］等，来获取系统线性化的低阶模型，得到相应传递函数，确定系统稳定运行域。该方法为进一步设计电力系统稳定器（Power System Stabilizer，PSS）提供一定的参考［10］。

3 无穷大电源存在小扰动时系统的机电振荡变化

电力系统中负荷的波动和励磁调速系统的不稳定性常给系统带来持续性小扰动［11］。在一定条件下，可能使系统出现大幅度的功率振荡，严重时出现增幅的功率振荡，导致系统失稳，甚至导致系统解列，如南方电网“4.26”振荡事故［12］。目前对此类事故的机理尚无明确的解释。

为探究此类小扰动导致的振荡现象，对图1中的仿真模型进行如下修改。

系统正常运行时，无穷大电源节点的电压为Vout，其表达式为

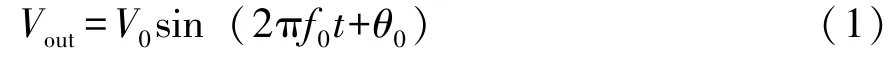
式中：V0、f0、θ0分别为系统稳定状态下，无穷大电源节点的电压、频率、相角值。

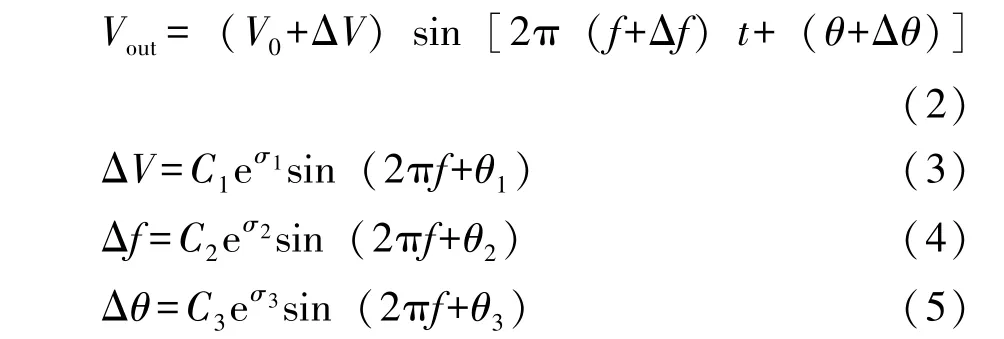
式中：C1、C2、C3分别为不同扰动量的幅值；σ1、σ2、σ3为衰减因子；θ1、θ2、θ3分别为不同扰动量的初相角。

在仿真模型中，改变无穷大电源节点内扰动量的扰动频率，即式（3）、（4）、（5）中的f，使之数值从0.1逐步增大2.0以上。

当C1＝0.1；C2＝C3＝0；σ1＝－0.01时，即无穷大电源节点只在节点电压V上存在一个小扰动ΔV时，系统机电振荡响应曲线如图4所示。

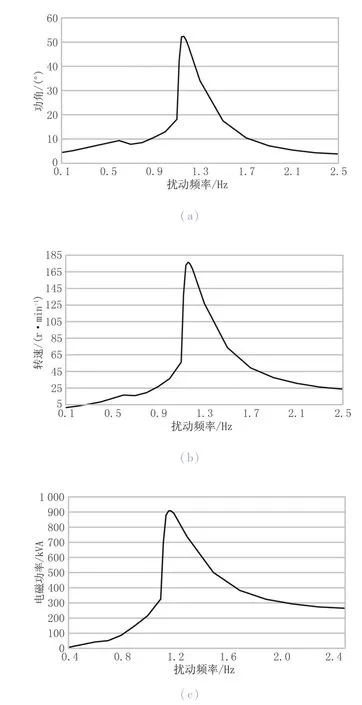
图4 无穷大电源电压有扰动时的系统响应曲线

令C＝0.05时，重复上述试验，发现响应曲线幅值变小，但总体变化趋势不变。当模拟Δf、Δθ扰动时，可得到相似结果。

由此可见，发电机组运行时，存在固有振荡频率。当系统扰动源的频率和系统固有振荡频率接近时，系统发生强迫功率振荡现象。本模型中，发电机组在1.1～1.2之间存在固有振荡频率，当扰动频率处于此区间时，系统振荡幅值最大。

4 结论

a.本文基于单机无穷大系统进行仿真，模型所加扰动量为6.5个周波时间时，系统失稳。

b.系统的非线性程度导致振荡过程中响应曲线的衰减速度不一致。非线性程度越高，衰减越快；反之，则越慢。

c.周期性的小扰动是导致系统出现强迫功率振荡的重要原因。系统的阻尼对振荡作用属于非决定性的，系统阻尼较强时，也会因扰动源的频率和系统固有频率接近而出现振荡幅值较大的机电振荡现象。

［1］ 陈冬霞.大电网低频振荡研究及其最新进展［J］.东北电力技术，2012，33（11）：33－37.

［2］ 王宇静，于继来.电力系统非线性振荡模态分析［J］.电力系统保护与控制，2010，38（20）：1－5，11.

［3］ 吴复霞，吴 浩，韩祯祥，等.电力系统非线性模式分析方法的比较［J］.中国电机工程学报，2007，27（34）：19－25.

［4］ 韩 松，何利铨，孙 斌，等.基于希尔伯特－黄变换的电力系统低频振荡的非线性非平稳分析及其应用［J］.电网技术，2008，32（4）：56－60.

［5］ 杨玉坤，席 皛，杨永华，等.基于Prony算法的高压电网故障与扰动信号的特征分析［J］.南方电网技术，2012，6（4）：63－67.

［6］ 汪 伟，江健武，钟建灵，等.基于分岔理论的铁磁谐振研究［J］.南方电网技术，2011，5（3）：56－60.

［7］ 李颖晖，张保会.正规形理论在电力系统稳定性研究中的应用—从非线性系统到线性系统的映射［J］.电力自动化设备，2003，23（6）：1－5.

［8］ 张伟年，张卫东.一个非线性电力系统的混沌振荡［J］.应用数学和力学，1999，20（10）：1 091－1 100.

［9］ 郝晓冬，王 峰.基于混沌理论的汽轮机组振动状态预测方法研究［J］.东北电力技术，2009，30（8）：46－50.

［10］ 蔡超豪，李 川，刘 宁.应用H_∞控制理论进行电力系统稳定器的设计［J］.东北电力技术，2000，21（7）：1－4，11.

［11］ 范 伟，赵书强.风电场接入电网强迫功率振荡研究［J］.东北电力技术，2009，30（1）：36－39，48.

［12］ 汤 涌.电力系统强迫功率振荡的基础理论［J］.电网技术，2006，30（10）：29－33.

Analysis on Nonlinear Phenomenon of Electro⁃mechanical Oscillations in Power System

MA Lie1，ZHANG Ying1，YU Yao1，GONG Na1，SUN Li⁃qian2
（1.Shenyang Institute of Engineering，Shenyang，Liaoning 110136，China；2.Nanjing NARI⁃Relays Electric Co.，Ltd.，Nanjing，Jiangsu 211111，China）

Electro⁃mechanical oscillations phenomenon in power system is accompanied by the expansion of the system network scale. It is important to research electrom⁃echanical oscillation for the security and stability analysis of region grid.Many conventional analysis methods use linear analysis，while ignoring power system itself is a strongly non⁃linear system，nonlinear characteristics inevitably have an impact on the response of electro⁃mechanical oscillations.In this paper，the nonlinear model is adopted to analyze the system response trajectories in the case of electro⁃mechanical oscillation and the cause of the response curve change is researched.

Electro⁃mechanical oscillations；Nonlinear；Time⁃domain simulation；Forced power oscillation

TM712

A

1004－7913（2015）10－0012－04

马 列（1983—），男，硕士，助教，主要从事电力系统机电振荡研究。

2015－06－15）