Realized GARCH模型在黄金期货市场的应用

王玲

Realized GARCH模型在黄金期货市场的应用

王玲

采用结合高频数据实现计量的Realized GARCH模型对黄金期货市场的杠杆效应、波动集群性等波动性特征进行研究。选取对价格稳健的实现计量作为Realized GARCH模型的解释变量，并对我国黄金期货的高频样本数据进行检验。极大似然方法估计结果表明：对价格跳稳健的实现双幂变差波动性（RBV）所得结果更优，黄金期货存在明显的杠杆效应和波动集群性，且波动具有长持续性，而实现方差并不能有效的刻画数据实际特征。

黄金期货 非对称性；Realized GARCH 极大似然估计

金融收益波动一般具有杠杆效应、集群性等。Engle（1982年）提出ARCH模型，解释了波动集聚效应，奠定了波动性度量的基础。Bollerslev提出的GARCH模型，能很好的刻画金融收益的异方差性和波动集群性，但不能说明金融资产收益的其他特性，如非对称性等。

为弥补GARCH模型的缺陷，描述利空、利好消息对收益波动影响和波动长记忆性的非对称GARCH模型应运而生。EGARCH模型、TGARCH模型、GJR-GARCH模型主要对收益的非对称性建模，FIGARCH模型描述了序列变动的异方差性和长记忆变动特性。

GARCH族模型虽然改进了条件方差方程，但所用日间数据损失了大量日内市场信息，势必造成结果的相应偏差。高频数据可提供更多的经济和市场信息，可得性显著提高，同时研究表明可用标准时间序列技术对“可观测”实现波动性建模。因此如果能充分利用数据自身包含的信息，即让数据尽可能的表现自己，并将这种信息嵌入到易于估计的模型中，则可期待精确的估计出资产收益的真实波动。越来越多的金融研究人员利用高频数据信息来度量资产收益波动的动态性。

一、文献综述

为充分利用高频数据的信息，主要从三个方面着手：（1）直接利用高频数据计量；（2）将高频数据计量嵌入已存在的模型中，对条件方差方程进行改进；（3）探索新的模型。徐正国、张世英（2004）利用上证综指的高频数据将调整已实现波动率和GARCH模型进行对比发现：实现波动率明显优于使用低频数据的GARCH模型。魏宇、余怒涛（2007）也证明使用高频数据的实现波动率模型比传统的低频数据模型好。文凤华（2012）等构建了AHAR-RV-V模型，并应用沪深300指数进行检验，结果表明模型能较好的捕捉股票市场波动的长记忆性和杠杆效应，且杠杆效应具有一定的持续性。田凤平等（2014）修正了已实现门阀多次幂变差，构建考虑跳跃的AHAR-C-CJ模型证明股指波动的连续性成分长记忆性较强，离散成分长记忆性较弱，模型显著提高了股指期货市场波动率预测精度。Louzis等（2014）用三种波动率模型：GJR-GARCH模型、实现GARCH模型、非对称HAR模型度量了股票、汇率、债券和黄金期货数据的波动率。本文在黄金期货高频数据基础上，利用Realized GARCH模型检验了市场波动的特征，并侧重采用价格稳健的实现计量。采用极大似然方法估计的结果表明：采用价格稳健的变量能更有效地捕捉市场的波动性特征。

二、波动率模型

1、实现波动率

最初主要采用参数方法来度量波动率，但理论和实践表明，可能由于样本包含的经济和市场信息不足等原因，参数方法都存在较大误差，不能精确度量波动率。因此国外新近研究将度量波动率的方法转向了利用高频数据的非参数方法上，本质是让数据尽可能的表现自己，并用收益的经验分布—而非假设的理论分布来度量波动，此类方法都有一个潜在的假设：未来与过去相同。最具代表性的就是实现波动性模型。迄今对实现波动性模型的研究表明：首先，对数实现波动性的非条件分布近似正态分布，但仍与正态分布有差距。其次，（对数）实现波动性是分整的。最后，实现波动是非线性的，即在ARCH型模型中也很常见的杠杆效应：过去的负冲击对当前（实现）波动的影响要大于正冲击。

Andersen等（2001）提出实现波动率，利用日内高频数据计算出事后波动率的“可观测”估计量，且已实现波动率估计量不依赖于任何模型，没有估计误差，可视为“可观测”变量。金融资产的日条件对数收益为rt＝p（t）－p（t－1）（其中p（t）是t天观察到的金融资产价格的对数），可表示为：

rt＝μt＋εt＝μt＋σtzt（1）（zt独立同分布于均值为0，方差为1的分布）。

通常市场微观噪声会引起日内收益的自相关，为了解释金融资产收益过程隐含的序列自相关性，如Giot和Laurent（2004）与Kuester（2006），用AR （1）对条件均值建模：E（rt│It-1）＝c＋φ1rt-1，条件期望解释了收益的动态时间依赖性和非零均值，而收益常常是异方差的，因此将典型特征嵌入到收益过程中是合理的。

2、Realized GARCH模型

GARCH模型和实现波动性模型各有自身的优势，如果能将GARCH模型的特性（灵活性等）与实现波动模型的优点结合，那么可以期待较准确的度量波动率。最初直接将实现波动性计量（实现方差、实现核等） 纳入 GARCH模型—GARCH-X模型，易于估计，操作简单，但只能用日收益数据提供波动性当前水平的单一信息，即实现计量是外生变量，不能用来更新波动性信息，是不完整的。为了改进这一点，人们开始尝试建立完整模型，Engle和 Gallo（2006），Sheppard和Shephard（2010）分别提出至少依赖两个隐变量的MEM和HEAVY模型。

Hansen等（2012）提出将实现波动性与收益联合建模的完整模型，即Realized GARCH模型。Realized GARCH模型可以调整由市场微观噪声和非交易时间所引起的实现波动的偏差，可以利用高频数据实现波动性计量方法更新波动性信息，而且波动能很快达到最新水平，本质上是一个离散时间随机波动率（SV）模型，由于实现测度的存在（构建了实现计量的封闭函数），可直接用极大似然方法同时估计收益和波动性等式的参数。其对数形式为：

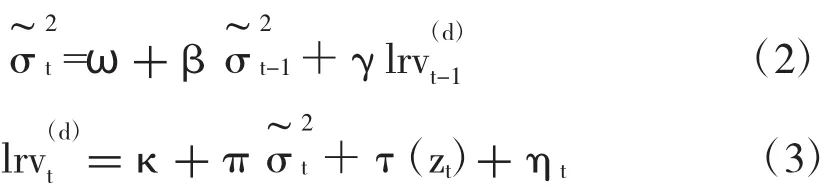
一般来说，我们期望真实日收益波动的无偏估计量能使K的估计值接近0，π的估计值接近1。但rt和σ2t是整日的收益和波动性，RVt是用日间开市时期数据计算的实现波动，因此，K应小于0，π应小于1。

金融资产价格常常存在跳跃性，为了克服价格中跳对积分波动率的影响，Barndorff-Nielsen和Shephard给出了已实现双幂变差波动率（RBV）：（t天的第j个连续复合日内收益为2，…M），M是日内收益的总数，t天的收益为rt＝实现波动性在不含微观噪声的情形下，无论真实资产过程是否具有跳，当抽样间隔趋于0时，RBV将趋近真实积分波动率，即RBV依概率收敛于积分波动率。而存在跳时，RV趋近于积分波动率加上跳跃部分，不再是积分波动率的一致渐近估计。

所有等式（等式（1）、（2）、（3））的参数都可以通过最大化实现波动性模型的联合对数似然函数来估计：

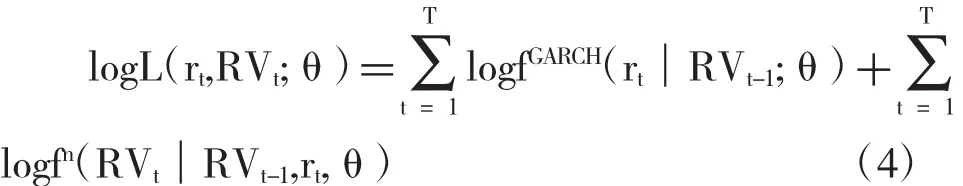
θ是参数向量，fGARCH（rt│xt-1,θ）是新息分布的密度函数，取决于GARCH式中zt的分布选择，fn（xt│xt-1，rt，θ）是相对于计算式的正态分布密度。当zt服从标准正态分布时，（4）式为

三、实证分析

1、数据的选取

金融数据常常受到市场微观噪声的影响，不同的采样频率会对结果产生不同影响，一般来说，实现波动率随着采样频率的降低而增大，直到采样频率降到5分钟，这种趋势才稳定下来。本文选择常用资产：商品中具有代表性的黄金期货2011-01-04—2014-07-04（848天）的5分钟数据。

2、描述性统计量

表1描述了日观察值和用于计算实现计量的日内收益数据的信息，也给出了资产的日（平方）收益，（对数）实现波动性和（对数）实现双幂变差波动的描述统计量。

表1 黄金期货全样本数据描述统计量表

由表1及图1、2、3可知：收益表现出明显的负偏性和厚尾性，峰度显著大于3。其值在0附近上下频繁波动，ACF图表明收益前后并无明显相关性，建模时将收益的条件均值设为0。收益平方ACF图表明收益平方前后相关性较大，即出现集群现象：大的波动跟随大的波动，小的波动跟随小的波动。

对数实现计量也表现出明显的前后依赖性。RVt、RBVt都表现出右偏和尖峰厚尾性；log RVt、log RBVt接近正态分布，log RBVt更接近正态分布，可能是因为RBVt对价格的稳健性，但JB统计量和QQ图表明两者均不服从正态分布。自相关函数（ACF）以双曲线形式缓慢衰减，表明所有（对数）实现波动序列表现出长期依赖性（即长记忆性）。图1、2、3显示，在2013.04-2014年间（恰好处于金价大幅跳水期），收益、收益平方、（对数）实现计量的波动最强。log RBVt的波动明显弱于log RVt。

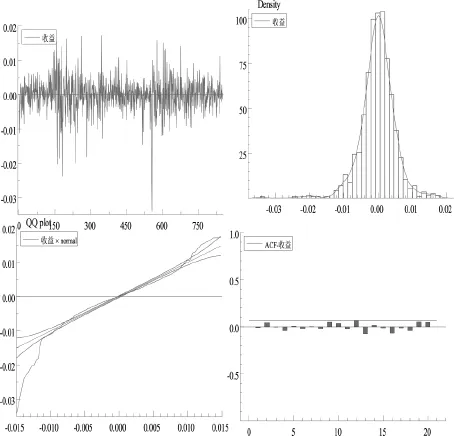
图1 收益rt相关图

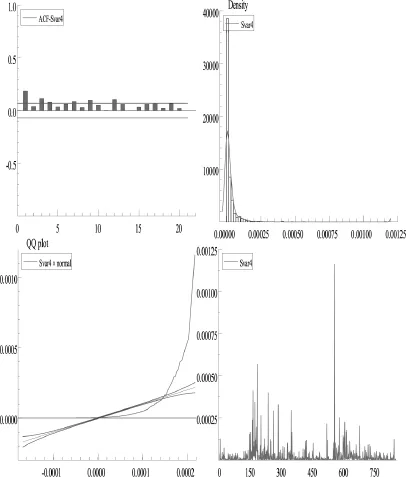
图2相关图

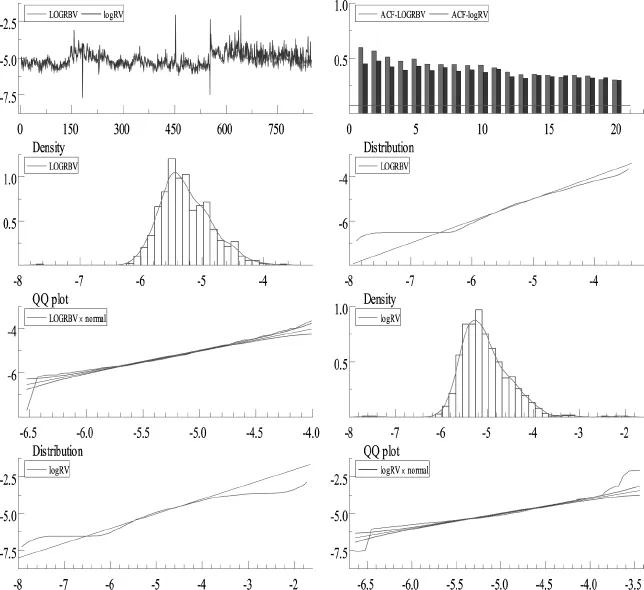
图3 实现计量相关图

3、模型估计结果

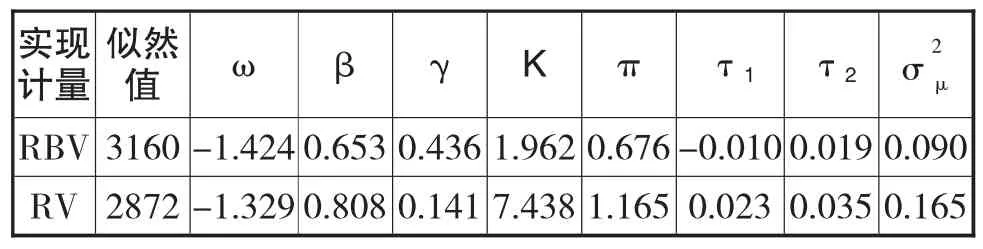
表2 Realized GARCH模型的参数估计结果

对比Hansen（2012）和Louzis（2014）的研究结果，RBV情形下，GARCH式的估计结果：β、γ的估计值接近其相关研究中估计结果的平均值。计量式中对数实现计量的估计，即π的估计值反映了其能解释的对数方差百分比，其值小于1，与先前预期吻合，所用只是开市时期数据，黄金期货并非24小时连续交易，对数RBV能解释真实方差对数的67.6%。K的估计值接近2，显然与先前假设不符合，实现计量不是未确定条件方差的无偏估计，可能由于中国黄金期货市场起步较晚，各方面体制并不健全，易受其他因素的影响。且RBV对价格跳稳健意味着其低于或等于由RV估计的价格过程的二次变分，所以由RBV所得的K估计值1.96小于采用RV所得的7.44。τ1的估计值为负，说明黄金期货市场存在杠杆效应；τ2的估计值为正，证明期货市场存在尺度效应，这与我们在收益序列中观察到的特性相符，杠杆函数估计结果验证了收益存在非对称性的典型特征。波动的持续性β＋γπ为0.95，表明波动的持续性较长。

在RV情形下，GARCH式的估计结果与先前研究相符，但是计算式的估计结果相差较大，特别是杠杆效应的估计值为正，与实际不符合，且实现计量是真实方差的有偏估计。持续性值为0.97，同样表明波动具有长持续性。总体来说，RBV的度量效果优于RV。

四、结 论

在GARCH模型中将实现波动性视为解释变量可用来评估用于衡量波动性的高频数据信息量。文中选用由高频数据计算的价格稳健实现计量RBV作为Realized GARCH模型的解释变量，对黄金期货收益的杠杆效应和波动集群性进行研究，并采用极大似然方法估计模型参数。

选取的黄金期货收益数据并没有自相关性（可能由于市场微观噪声对黄金期货市场收益的影响较小），建模时收益的条件均值设为0。利用RBV进行分析时，β、γ的估计值接近相关研究中估计结果的平均值。τ1估计值为负，杠杆效应明显存在；τ2估计值为正，即存在波动集群性；τ1、τ2估计结果表明黄金期货市场并非完全有效，冲击对于波动的影响具有非对称性。π的估计值较大，证明对数RBV可解释的对数波动的比例较大，由于交易时间的制约，其估计值小于1，符合先前假设。然而，采用RV进行分析的结果不尽理想，尤其τ1的估计值为正，显然与预期相悖。但两变量同时表明波动具有长持续性。

总体来说，在新息和计量式误差项正态分布假设条件下，采用RBV估计的结果优于RV，可能归因于RBV对价格跳稳健的特性，波动相对较弱，取其对数后更接近正态分布。

［1］Giot P.,Laurent S..Modeling daily value-at-risk using realized volatility and ARCH type models.Empirical Finance.2004（11）379-398

［2］ Louzis D.P.,Xanthopoulos-Sisinis S.,Refenes A.P..The role of high-frequency intradaily data,daily range and implied volatility in multi-period Value-at-Risk forecasting.Forecast.2013.32（6）561-576

［3］Louzis D.P.,Xanthopoulos-Sisinis S.,Refenes A.P..Realized volatility models and alternative Value-at-Risk prediction strategies.Economic Modeling.2014.40:101-116

［4］王天一，黄卓.高频数据波动率建模—基于厚尾分布的Realized GARCH模型.数量经济技术经济研究.2012 （5）149-161

［5］田凤平，杨科，林洪.沪深300指数期货已实现波动率的跳跃行为.系统工程.2014.32（2）

［6］瞿慧，刘烨.沪深300指数收益率及已实现波动联合建模研究.管理科学,2012,25（6）101-110

［7］文凤华，刘晓群，唐海如，杨晓光.基于LHAR-RV-V模型的中国股市波动性研究.管理科学学报.2012.15（6）59-67

［8］Hansen P.R.,Huang Z.,Shek H..Realized GARCH:A JointModelofReturns and Realized Measures of Volatility.Journal of Applied Econometrics,Forthcoming. 2012,27（6）877-906

［9］赵华.中国股市的跳跃性与杠杆效应—基于已实现极差方差的研究.金融研究.2012（11）179-192

［10］王天一，赵军，黄卓.利用高频数据预测沪深300指数波动率—基于Realized GARCH模型的实证研究.世界经济文汇.2014（5）17-30

［11］Engle R.，Bollerslev T..Modeling the persistence of conditional variance.Econometric Reviews.1986.5:1-50

［12］MichealNwogugu.Furthercritique ofGARCH/ARMA/VAR/EVT/Stochastic-Volatility models and related approaches. Applied Mathematics and Computation, 2006,182:1735-1748

［13］沐年国.GARCH-Jump模型对跳行为捕捉能力的讨论稳定分布及其在GARCH中的应用.上海理工大学学报. 2007.29（1）32-36.

［14］Pilar Abad,Sonia Benia,Carmen Lopez.A comprehensive review of Value at Risk methodogies.The Spanish Review of Financial Economics.2013

［15］Corsi F..A simple approximate long memory model of realized volatility.JournalofFinancialEconometrics. 2009.7:174-196

［16］Lunde A.,Hansen P..A forecast comparison of volatility models:does anything beat a GARCH（1,1）.Journal of Applied Econometrics.2005.20（7）873-889

［17］Martens M.,Dijk D.,Pooter M..Forecasting S&P 500 volatility:long memory,level shifts,leverage effects,day of the week seasonality and macroeconomic announcements.International Journal of Forecasti-ng.2009.25: 282-303

Application of Realized GARCH Model in Gold Future Market

WANG Ling
University of Shanghai for Science and Technology,Shanghai 200093

This paper studies the leverage effect and volatility clustering of gold future in China by using realized GARCH model combined with realized measures calculated from high-frequency data.The realized measure robust to price jumps is selected as the explanatory variable of realized GARCH model to test the features of high-frequency data of gold future in China.The results got from maximum likelihood estimation show:the Realized Bipower Variation (RBV)which robust to price jumps performs good,gold future presents leverage effect and volatility clustering,and volatility lasts a long time;but Realized Variance(RV)can't describe the real characters of the data effectively.

Gold Future,Asymmetry,Realized GARCH,Maximum Likelihood Estimation

F831

A

王玲，女，汉族，安徽淮南人，上海理工大学硕士研究生，研究方向：金融统计；上海，200093