基于广义逆算法的电压暂降状态估计

王佳兴，杨洪耕，王泽，韩斐

(四川大学电气信息学院，四川成都610065)

基于广义逆算法的电压暂降状态估计

王佳兴，杨洪耕，王泽，韩斐

(四川大学电气信息学院，四川成都610065)

提出了一种基于广义逆算法的电压暂降状态估计(VSSE)新方法，将传统的随机故障点法和解析法相结合得到电压暂降状态估计方程。克服了传统随机故障点法选取故障点位置和数量的盲目性，具有在减少计算量的同时且能保证评估精度的优点，并利用广义逆算法准确可靠地求解此欠定方程组。相对于整数线性规划和遗传算法，该方法无需迭代，不存在收敛性问题，且计算复杂度小，计算历时少。另外由于该算法本身没有参数约束问题，克服了遗传算法在交叉和变异过程中选取参数时依靠人为主观经验的缺点。利用该方法在IEEE-30标准节点系统上进行仿真计算，并与遗传算法对比，结果验证了本文方法的准确性和可靠性。此方法适用于任何规模电网发生对称故障和不对称故障时的电压暂降状态估计。

电压暂降状态估计;随机故障点法;解析法;遗传算法;广义逆

1 引言

随着电力电子技术飞速发展，各种敏感、变频设备在电力系统中的广泛应用，电压暂降问题现已成为威胁设备安全和正常稳定运行的严重动态电能质量问题。即使短时电压暂降也可能引发敏感设备故障或停运，造成重大的经济损失［1］。本文主要采用电压暂降频次［2］作为指标来准确刻画和估计电网中电压暂降信息。

母线节点上安装电能质量监测仪可直接记录此节点发生的电压暂降频次，但出于经济性考虑，为使电网建设成本最小化，优化配置后电网中监测仪安装的数量变得有限［3-6］，如何利用监测节点发生的电压暂降频次来准确估计未装监测设备母线节点的暂降频次，进而获得整个电网的电压暂降信息，是一项具有重要现实意义的研究课题［7-9］。

系统故障受网络拓扑、故障类型、故障点、故障阻抗、变压器接线方式等多种不确定性因素影响，增加了评估难度。现有方法主要分两类:基于实测的统计分析法［6，8-10］和基于随机建模的随机估计法［7-9］。实测统计法合理的精确度需要很长的测量周期，需要安装监测设备，成本较高，且统计故障率易受天气因素、绝缘子污秽程度以及人为因素等外界影响［11］。随机估计法主要分临界距离法和随机故障点法［9］。基于此我国学者王宾较早提出电压暂降状态估计方法［4］，该方法采用最小二乘法搜索故障点所在路径，进而估计非监测点电压暂降幅值特征，但该方法只局限于简单辐射性电网，不适用于环网;文献［9］采用随机故障点法将线路故障段均一划分得到电压暂降状态估计方程，但此方法获取较高的精确度需要设置较多的故障点，计算量较大，并且对如何合理地设置故障点数目和位置至今没有统一标准。本文将解析法［12，13］和随机故障点法相结合，利用节点阻抗矩阵，根据电压暂降幅值对传输线故障距离的解析式计算得到各种短路故障情况下各电压限值对应的临界故障点，合理划分线路故障区间可大量减少计算量的同时满足评估精度的要求。

2 VSSE的基本原理

状态估计中，通用的数学表达式为:式中，H为量测矩阵，本文和文献［5］相似，H中每个元素表示装有量测设备的母线节点记录的电压暂降频次，暂降电压对应于一个预先设定的临界电压值;状态变量X基于故障位置的概念，X中每个元素表示线路故障区间发生故障频次［14］;M为量测量和状态变量的关系矩阵;I为测量误差，可忽略不计［8］。式(1)中相关变量矩阵具体形成阐述如下。

3 VSSE建模

首先，假设电网有N个节点，L条支路，监测仪的数量设为C，显然，本文讨论的问题中C＜N。

3.1 量测矩阵H的建立

H由C个监测仪记录量测的电压暂降频次数据直接形成。通常，暂降表示故障发生时母线残余电压小于预先设定的临界电压值。若是三相不对称故障，母线残余电压取其中电压幅值最小的一相。

给定一个临界电压值V，得到相对应的量测量HV。HV中每个元素表示母线残余电压低于临界电压值V时相应的监测仪记录的暂降次数。因此，HV中共包含C个元素，且都为整型。

3.2 状态变量矩阵X的建立

随机故障点法的基本思想为:预先随机设定系统中的故障点，通过计算这些故障点故障所引起的电压暂降，来具体分析其具体的特征量信息。如图1所示，图中横轴代表故障线路的百分比，t1表示预先设定的临界电压阈值。若故障点数选取过少，线路故障区间随机划为0～p1，p1～p2，p2～1，由于实际母线电压包含在p1～p2区间内，这对于发生在p1～p2区间故障点检测与估计将造成不准确，进而导致评估结果精度变差。反之一味增加故障点数则会加大计算冗余度。如何设置故障点的位置与数目对电压暂降状态估计分析计算至关重要。

图1 母线电压实际值和估计值Fig．1 Actual and estimated bus voltage

为了合理划分线路故障区间，可以利用解析法分析系统短路故障，基本原理如图2所示。假定线路p-q上的节点r处发生故障，节点k为监测点。

图2 电网示意图Fig．2 Schematic diagram of grid

监测点处的电压Ek根据叠加原理可以用故障前的电压Ek0和节点阻抗矩阵表示:

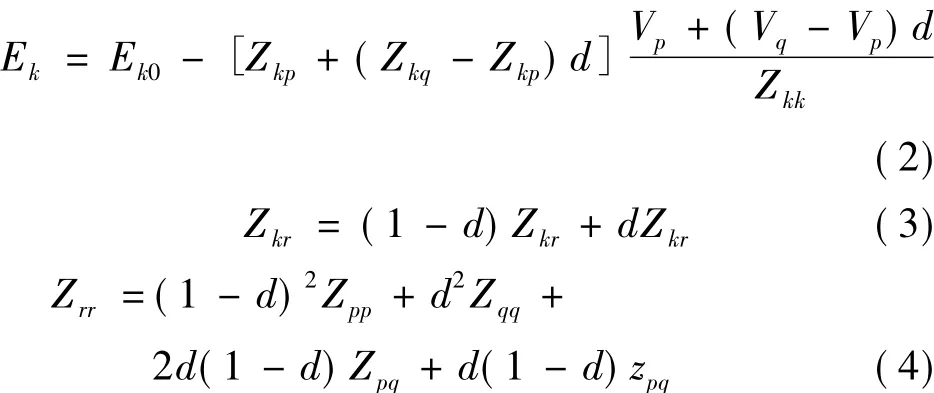
式中，Zkr、Zkq、Zkp、Zpq分别为阻抗矩阵Z中节点k、r、p、q间的互阻抗;Zrr、Zpp、Zqq代表节点r、p、q的自阻抗;zpq代表线路p-q段的阻抗。

基于此，本文将解析法和故障点法相结合合理确定线路故障区间。如图3所示，为简单起见，此事例中只包含一条被监测的母线m1和一条待估计母线m2，图中表示系统中沿某条线路li发生故障时在母线m1和m2求得的残余母线电压的幅值。对于预先设定的电压阈值为t1，利用上述方法推导得到系统故障时节点电压对输电线路故障距离的函数表达式，再对应不同的电压暂降临界值得出线路上的临界故障点，将线路li划分为0～p1，p1～p2，p2～p3，p3～1四个区段。

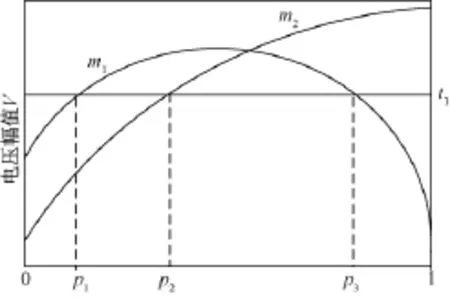
图3 线路li故障在母线m1和m2产生的残余电压Fig．3 Bus residual voltage at m1and m2with failure occurred in line li

用上述方法遍历系统中所有线路L则可获得全网在电压阈值t1下线路总的故障区间P1。状态变量矩阵X1中每个元素表示每个故障区间内发生的故障次数。

3.3 关系矩阵M的建立

由式(1)可知，矩阵M1(对应临界电压值t1)表示状态变量矩阵X1与量测量矩阵H1之间的关系。建立M1具体步骤如下:

(1)由3.2节方法求得全网在电压阈值t1下线路总的故障区间P1;

(2)根据电网的参数和拓扑结构，随机模拟发生P1个故障区间内短路故障。

(3)分别计算出故障区间P1内发生短路故障时在C个安装在母线节点监测仪记录的母线残余电压。

将计算得出的电压值与相应的临界电压值比较形成关系矩阵M1。M1为二进制矩阵，M1中每个元素对应一条被监测母线与一个故障区间发生故障的关系，其值为1或0，即:

式中，A表示故障区间p发生故障时在监测母线产生的残余电压低于临界电压值t1;B表示故障区间p发生故障时在监测母线产生的残余电压高于临界电压值t1。

通过图3，易理解M1的形成，图中假设只有一条被监测的母线m1，则M1为:

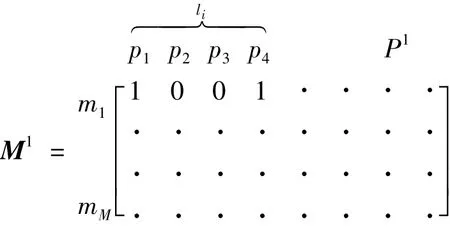
由于p1，p4所在故障区间内发生故障求得母线m1残余电压小于t1，则m1(1，1)=m1(1，4)=1，同时表示在母线m1引发电压暂降;

同理m1(1，2)=m1(1，3)=0，因为在p2所在故障区间内发生故障求得母线m1残余电压大于t1，表示未引发母线m1电压暂降。

考虑整个电网所有输电线路，新的列将被加入矩阵M1，每一列对应线路的一个故障区间。值得注意的是，矩阵M1仅仅取决于被考虑电网的性质，对于一个给定电网和一个给定临界电压值只需要估算一次。

需要说明的是，电网中监测仪的安装数量与位置会影响VSSE的精度，本文监测仪安装配置采用文献［6，12］的方法，保证系统中任何位置发生故障至少能被一台监测仪测量记录。如此，M1中每列至少包含一个非0元素，即M1行满秩。

3.4 VSSE一般化

设定一个临界电压值t，则

考虑整个电网，VSSE一般形式为:

式中，Ht1，Ht2，…，HtT为量测量，表示在监测母线在给定临界电压值t=t1，t2，…，tT时监测仪记录相对应的电压暂降频次;Mt1，Mt2，…，MtT为临界电压值t =t1，t2，…，tT时相对应的二进制关系矩阵;X为状态变量。

式(3)可简化写为:

4 基于广义逆算法求解VSSE

4.1 状态变量X的求取

传统的状态估计方程往往是超定的，然而由于量测量不足，本文中由于监测仪的数量少于母线节点数，即C＜N，式(7)为欠定方程或者叫病态方程。针对该问题，文献［12］采用了整数线性规划(ILP)的方法，但此方法求解速度较慢，文献［15，16］分别采用神经网络算法(ANN)和遗传算法(GA)通过迭代寻优的方法求解欠定方程组，相比ILP算法提高了计算效率。但GA算法对于求解高维度、多局部极值复杂问题，在迭代的过程中可能导致算法陷于局部最优的情况，在收敛速度和精度上难以达到期望要求［9］，且该方法在交叉和变异时参数的选择目前大部分依靠主观经验，这严重影响解的品质。基于此本文则采用广义逆算法［15-17］，此方法本身没有算法参数约束问题，且相对于ILP、ANN、GA算法，该方法不需要迭代，不存在收敛性问题，由于此方法计算复杂度较小，计算历时明显减少，同时也适合任何复杂电网。

基于广义逆算法理论，对于式(7)，易证明关系矩阵M满足Moore-Penrose方程［9］，本文中由于优化配置使得电网中任意位置发生故障至少能被一台监测仪所检测，因此关系矩阵M中每列元素至少有一个非零元素，即M行满秩，所以存在M的Moore-Penrose逆为［11］:

定理可证明方程组MX=H为欠定方程组时，解X=M+H不但是最小二乘解，而且是具有极小范数的最小二乘解，或最佳逼近解［12，16］，简记为LNLS解。利用广义逆算法的求解结果实质上是满足以下约束条件:

式中，min‖x‖_2表示状态变量的最小二次范数。

4.2 电压暂降频次的估计

式中，A表示故障区间p发生故障时在未被监测母线产生的残余电压低于临界电压值t;B表示故障区间p发生故障时在未被监测母线产生的残余电压高于临界电压值t。

结合式(10)，则式(11)转化为:

5 算例仿真

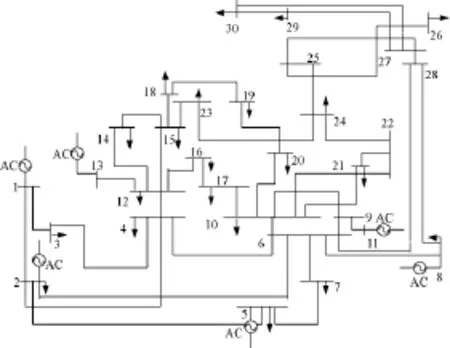
图4 IEEE 30节点标准测试系统Fig．4 IEEE 30 nodes standard test systems

图5 母线节点发生暂降频次(电压阈值设为0.7pu)Fig．5 Bus node voltage sags (voltage threshold is set to 0.7pu)

图6 母线节点发生暂降频次(电压阈值设为0.9pu)Fig．6 Bus node voltage sags (voltage threshold is set to 0.9pu)

图7 母线节点发生暂降频次(电压阈值设为0.8pu)Fig．7 Bus node voltage sags (voltage threshold is set to 0.8pu)

利用上述方法应用于IEEE30节点标准测试系统，系统数据由文献［18］提供，电网接线图如图4所示，由6个发电厂、30条母线、37条传输线和10台变压器组成。本文模拟故障为三相短路故障，不对称故障参看文献［15］，本文不再赘述。利用GA算法和广义逆算法仿真结果对比如图5～图7所示。

图5～图7分别描绘电压阈值设置为0.7pu、0.9pu、0.8pu时实际母线电压暂降频次和估计的暂降频次，误差结果见表1和表2，误差定义为:

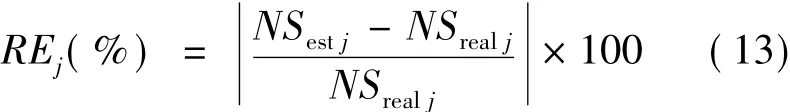
表1 IEEE30节点仿真结果误差Tab．1 IEEE30 nodes simulation result error

表1和表2误差结果表明广义逆算法精度明显优于遗传算法，利用该方法估计出平均电压暂降频次和实际值非常接近，其有效性和准确性显著。表3为针对不同阶数网络两种算法在Matlab中运算时间结果对比。从表3明显可以看出，由于广义逆算法无需迭代，计算历时相比遗传算法大幅度减少，比如针对IEEE-30节点电压阈值设为0.7pu时，运用GA算法需要1087s，但通过广义逆算法只需要9.53s的短暂时间。

表3 不同阶数网络运算时间对比Tab．3 Contrast of calculation time for different orders network (单位:s)

另外，注意到随着设定电压阈值的降低，平均误差也随之升高，这是由于电压阈值设置越低，对应监测仪的监测范围随之减小，评估结果误差会相应增加。

6 结论

本文提出一种电压暂降状态估计的新方法，将解析法和传统故障点法相结合得到电压暂降状态估计方程，并利用广义逆算法有效求解该欠定方程组。利用该方法在IEEE30标准测试系统中仿真测试，并与遗传算法对比，结果表明本文所提方法的可靠性和准确性。另外针对不同网络阶数在Matlab仿真求得GA算法和广义逆算法运算时间对比，结果表明广义逆算法计算历时明显小于遗传算法。值得注意的一点是，在形成关系矩阵时维数相对较大且未考虑故障传播时变压器设备及保护装置的投切等因素对电压暂降的影响，可能在一定程度上会影响实际结果的准确性。

［1］李妍，余欣梅，熊信艮，等(Li Yan，Yu Xinmei，Xiong Xinyen，et al．)．电力系统电压暂降分析计算方法综述(Voltage sag analysismethod to calculate the electric power system)［J］．电网技术(Power System Technology)，2004，28(14):74-78．

［2］IEEE Standard 1564-2003，The IEEE voltage sags indices［S］．

［3］G Olguin，F Vuinovich，M H JBollen．An optimalmonitoring program for obtaining voltage sag system indexes［J］．IEEE Transactions on Power Systems，2006，21 (1):378-384．

［4］代晓倩，杨洪耕，蔡维(Dai Xiaoqian，Yang Honggeng，CaiWei)．一种考虑电压暂降分布域的电能质量监测仪的优化配置方法(Consider a voltage sag distribution domain of the optimal allocation of power quality monitor method)［J］．电力科学与工程(Electric Power Science and Engineering)，2011，27(2):6-12．

［5］E Espinosa-Juarez，A Hernánde Z，G Olguin．An approach based on analytical expressions for optimal location of voltage sagmonitors［J］．IEEE Transactions on Power Delivery，2009，24(4):2034-2042．

［6］吕伟，田立军(Lv Wei，Tian Lijun)．基于凹陷域分析的电压暂降监测点优化配置(Optimal allocation of voltage sagmonitoring based on exposed area analysis)［J］．电力自动化设备(Electric Power Automation Equipment)，2012，32(6):45-50．

［7］BWang，W Xu，Z Pan．Voltage sag state estimation for power distribution systems［J］．IEEE Transactions on Power Systems，2005，20(2):806-812．

［8］E EspinosaJuárez，A Hernández．A method for voltagesag state estimation in power systems［J］．IEEE Transactions on Power Delivery，2007，22(4):2517-2526．

［9］M R Qader，M H JBollen．Stochastic prediction of voltage sags in a large transmission system［J］．IEEE Transactions on Industry Applications，1999，35(1):152-162．

［10］JV Milanovic，M T Aung，C PGupta．The influence of fault distribution on stochastic prediction of voltage sags［J］．IEEE Transactions on Power Delivery，2005，20 (1):278-285．

［11］Park CH，Jang G，Thomas R．The influence of generator scheduling and time-varying fault rates on voltage sag prediction［J］．IEEE Transactions on Power Delivery，2008，23(2):1243-1250．

［12］E Espinosa，A Hernández．An analytical approach for stochastic assessment of balanced and unbalanced voltage sags in large systems［J］．IEEE Transactions on Power Delivery，2006，21(3):1493-1500．

［13］封磊，蔡创，齐春，等(Feng Lei，Cai Chuang，Qi Chun，et al．)．PSO和GA的对比及其混合算法的研究进展(The contrast of PSO and GA and their research progress of hybrid algorithm)［J］．控制工程(Control Engineering of China)，2005，5(12):89-92．

［14］E EspinosaJuárez，A Hernández．Voltage sag state estimation:An approach based on the concept of fault positions［A］．International Conference on Power Quality［C］．Cascais，Portugal，2006．3-9．

［15］王松桂，杨振海(Wang Songgui，Yang Zhenhai)．广义逆矩阵及其应用(Generalized inversematrix and its application)［M］．北京:北京工业大学出版社(Beijing: Beijing University of Technology Press)，1996.178-181．

［16］尹钊，贾尚晖(Yin Zhao，Jia Shanghui)．Moore-Penrose广义逆矩阵与线性方程组的解(Moore-Penrose generalized inversematrix and the solution of linear equations)［J］．数学的实践与认识(Mathematics in Practice and Theory)，2009，39(9):239-244．

［17］杨桂元(Yang Guiyuan)．广义逆矩阵的应用(Application of generalized inversematrix)［M］．北京:高等教育出版社(Beijing:Higher Education Press)，2007. 198-204．

［18］Maeda A，Kaya Y．Game theory approach to use of noncommercial power plants under time-of-use pricing［J］．IEEE Transactions on Power Systems，1992，7(3):18-19．

M ethod of voltage sag state estimation based on generalized inversematrix

WANG Jia-xing，YANG Hong-geng，WANG Ze，HAN Fei
(School of Electrical and Information，Sichuan University，Chengdu 610065，China)

A new method of voltage sag state estimation based on the generalized inverse algorithm is presented in this paper．To combine traditional stochastic fault pointmethod and analyticmethod，voltage state estimation equation is obtained．And itovercomes the blindness of traditional stochastic fault pointmethod to select fault point location with a decrease in the amount of calculation and evaluation aswell as guaranteeing the accuracy of the estimation．And by using the generalized inverse algorithm to solve the underdetermined equations accurately and reliably，relative to the integer linear programming and genetic algorithm，the method needs no iteration，and there is no convergent problem，so itneeds less time to calculate．In addition，because the algorithm itself has no parameter constraint problem，it overcomes the shortcomings of selecting genetic algorithm parameters in the process of crossover and mutation depending on human experience．The proposed estimation method has been validated by using the IEEE 30 test system and the results obtained have been very satisfactory．The proposed method is applicable to voltage sag state estimation in any size gridswhen symmetric and asymmetric faults occur．

voltage sag state estimation;stochastic fault pointmethod;analyticalmethod;genetic algorithm;generalized inverse

TM743

A

1003-3076(2015)04-0018-06

2014-02-18

王佳兴(1989-)，男，四川籍，硕士研究生，主要研究方向为电能质量分析与控制、电压暂降状态估计;杨洪耕(1949-)，男，四川籍，教授/博导，从事电能质量分析与控制、区域电压无功控制等方面的研究与教学工作。