基于Markov三级库存系统备件横向调拨配置模型
2015-06-05徐廷学丛林虎
董 琪,徐廷学,丛林虎
(1.海军航空工程学院研究生管理大队,山东烟台264001;2.海军航空工程学院兵器科学与技术系,山东烟台264001)
基于Markov三级库存系统备件横向调拨配置模型
董 琪1,徐廷学2,丛林虎1
(1.海军航空工程学院研究生管理大队,山东烟台264001;2.海军航空工程学院兵器科学与技术系,山东烟台264001)
针对特装器材库存系统内仓库间备件横向调拨问题,提出了基于Markov三级库存系统备件横向调拨配置模型。通过考虑基层级仓库故障件的部分修复情况,根据Markov排队理论,建立了基层级仓库分系统库存模型,得到基层级仓库库存稳态概率。对库存系统内各级进行整合,建立了三级库存系统横向调拨配置模型,结合费用参数,对该模型进行优化,构建了以期望配置总费用最小为目标、以库存容量为约束的三级库存系统横向转运费用模型。运用迭代算法和Lingo软件对模型进行求解。通过实例分析,得到横向调拨下最优配置方案产生的费用为非横向调拨下的14.55%,验证了所建模型和算法的合理性。最后,对影响库存配置的参数进行了灵敏度分析,确定了各参数对优化目标的影响程度。
备件配置;马尔可夫排队模型;横向调拨;库存优化
0 引 言
备件供应保障的主要目标不仅是提高备件供应效能,同时还要降低供应保障费用。库存站点间备件的横向调拨不仅可以提高保障效能,而且利用库存共享的原理,降低了库存站点总库存量,进而将供应保障费用控制在较低的水平[1]。目前,海军舰船特装器材供应保障模式是逐级调拨,即本级仓库的备件均由上级仓库进行补充。这种保障模式随着舰船装备发展及训练的范围和强度不断增加而产生了保障能力不足、特装器材配置不合理等诸多问题。因此,需要研究科学的特装器材横向调拨配置方法,确定最优的特装器材配置方案,以最少的经济投入,实现保障系统效能和舰船装备可用度最大化。
当前国内外对备件横向调拨配置开展了大量的研究,取得了较大进展。一方面,研究者们以METRIC模型[2]为理论基础,研究单级或两级库存系统横向配置问题。文献[3]研究了分布式零售站点间的紧急调拨问题,确定了站点规模与费用、订购策略之间的关系;文献[4- 5]通过利用动态规划方法求解横向调拨下的配置方案;文献[6- 9]利用仿真、蚁群算法、随机规划模型等方法求解库存系统的备件横向配置模型。另一方面,部分研究者研究了横向调拨策略与备件配置方案的关系,以确定出不同情况下的最优横向调拨策略。文献[10]将横向调拨策略主要分为主动型和被动型两种;文献[11- 12]提出了预防性横向调拨策略,并进一步扩展,考虑库存重分配情况下的最优横向调拨策略;文献[13]提出了利用准近视法确定最优被动横向调拨策略。
尽管针对备件横向调拨配置的研究开展较为广泛,但多数METRIC横向配置模型以Palm定理为基础,适用于故障件均可被修复,而本文考虑只有部分故障件可修复的情况。Markov模型只考虑库存状态和状态转移的特点,无需考虑故障件是否全部被修复,较适合于解决部分故障件可修复情况下的备件横向调拨问题。目前仅文献[14]利用Markov过程理论研究单级多站点备件横向调拨下的库存决策问题,但未考虑多级库存系统的情况。因此,本文在现有舰船特装器材三级保障模式的基础上,针对基层级仓库间允许横向调拨,利用Markov理论开展优化配置方法研究,构建三级特装器材库存系统横向调拨配置模型。结合费用指标,建立相应的优化模型。
1 问题的描述
1.1 问题描述
某特装器材库存系统可看作一个三级库存系统,包括基地级仓库、中继级仓库和基层级仓库,具体库存系统结构如图1所示。
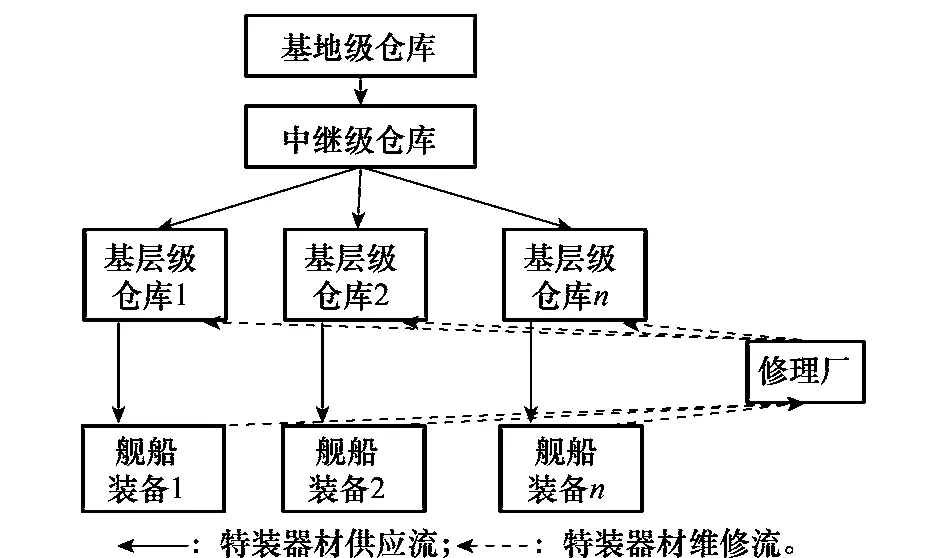
图1 特装器材库存系统
由图1分析可知,该库存系统由一个基地级仓库、一个中继级仓库和若干基层级仓库组成,但在特装器材的保障过程中考虑了维修因素,增加了修理流程。具体保障流程如下:n个特装器材基层级仓库分别对应保障n个舰船装备,且每个舰船装备因故障产生的需求服从独立的Poisson过程,均值为λi(i=1,2,…,n);中继级仓库负责对各基层级仓库进行特装器材补充,同理,基地级仓库负责中继级仓库的特装器材补充。舰船装备产生的故障件经过修理厂维修,修复的特装器材送回至原基层级仓库,该过程同样服从独立的Poisson过程,均值为σ,且考虑修理厂的修复率为ρ(0<ρ<1)。与此同时,在基层级特装器材保障过程中,存在横向调拨情况,即当某基层级仓库出现库存短缺时,可从其他基层级仓库进行器材调拨,补充至该短缺仓库。
1.2 基本假设
为建立特装器材配置模型,作如下假设:
(1)各基层级仓库的最大库存容量均为S,中继级仓库的最大库存容量为C,基地级仓库可充分保障中继级和基层级仓库的特装器材需求,即库存容量无限;
(2)库存系统中每个仓库的库存控制策略为(s-1,s);
(3)需求首先由对应保障的基层级仓库满足,同时向中继级仓库申请补货,补充的时间服从均值为μ-1的指数分布,若此时修理厂将修复器材送回至该仓库,则无需向中继级申请补货;
(4)基层级仓库间的横向调拨采取随机选择策略,即在库存容量为正的仓库间选择;
(5)若所有基层级仓库均发生库存短缺,则此时产生的需求直接由中继级仓库满足,同时中继级仓库向基地级仓库申请器材补充,补充时间服从均值为γ-1的指数分布;
(6)若基层级仓库和中继级仓库同时发生短缺,则此时产生的需求将由基地级仓库满足;
(7)故障器材维修后,产品修复如新,且维修时间相互独立;
(8)修理厂的维修渠道无限,故障器材在维修过程中不存在排队等待现象;
(9)与上下级器材补充的时间相比,横向调拨的时间可忽略不计。
2 基层级库存模型构建
2.1 模型参数
在考虑横向调拨情况下,基层级仓库的保障水平可由以下参数表征:
pi:基层级仓库i无法满足需求的概率;
αi:基层级仓库i对应的需求通过其他基层级仓库横向调拨得到满足的概率;
βi:需求由基层级仓库i库存满足的概率;
θi:基层级仓库i对应的需求无法得到满足的概率。
由参数含义可知,得到以上参数间的关系:

2.2 θi参数模型
由于基层级仓库间可以通过横向调拨来满足舰船装备对特装器材的需求,若存在基层级仓库i对应的需求无法得到满足的情况,说明所有基层级仓库的库存量均为零,都无法满足此时舰船装备对特装器材的需求,因为只要任一基层级仓库有库存,则需求就能满足。因此,基层级各仓库的θi满足以下关系:

式中,θ为基层级仓库无法满足需求的概率。

2.3 βi参数模型
令xi为时间t内基层级仓库i由其他基层级仓库横向调拨得到满足的需求,于是有

由横向调拨得到满足的需求与自身库存满足的需求比率为

基层级仓库i有库存条件下的总需求率为
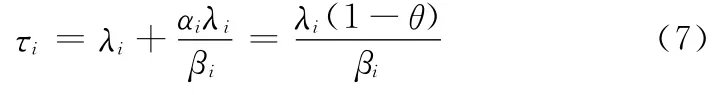

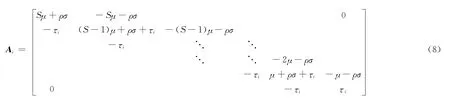
状态转移矩阵Ai与状态空间pi满足以下关系:

由式(8)和式(9)可得

由βi定义可知

因为τi=λi(1-θ)/βi,则令
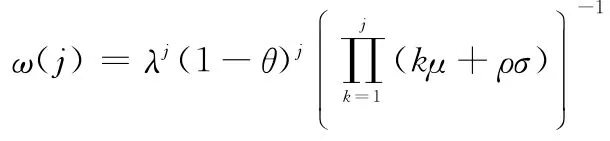
于是有

2.4 模型求解
综上可知,4个模型参数不能通过各自的表达式计算得出,需要通过将式(1)、式(2)、式(4)和式(12)联立计算得到。
由Markov排队理论可知,在求解过程中,若μ+ρσ<λi,即需求率大于补充率,则无法保证极限概率的存在和联立方程解的唯一性,证明过程见文献[15]。因此,需明确联立等式成立的条件,即μ+ρσ≥λi。
3 三级库存系统配置模型及求解
3.1 配置模型构建


图2 库存系统整合模型
根据中继级仓库和基层级仓库的库存容量,可得到库存系统状态空间的状态总数,即(C+1)(nS+1),且状态变量为
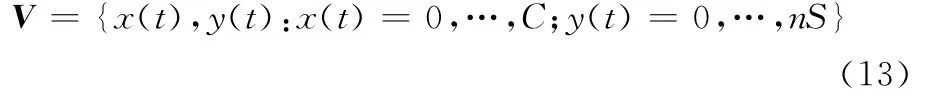
通过将库存系统的库存水平按照升序排列,构建出系统稳态概率分布q,即

通过构建库存系统状态转移率矩阵B,使得B和q满足下列关系[15]:
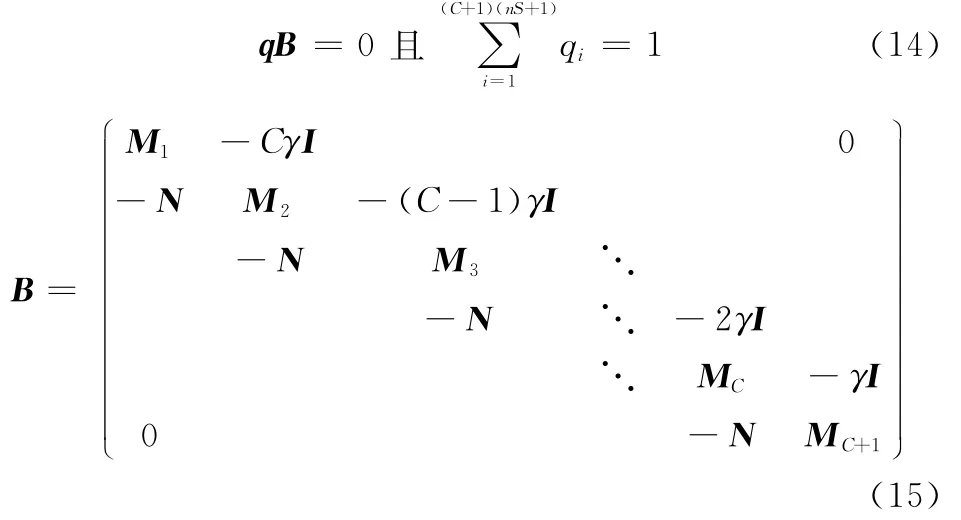
式中,I为(nS+1)(nS+1)维单位矩阵。

由于库存系统的状态形式是一个不可约的Markov链,因此,根据Markov极限特性可知[18],该系统的稳态概率分布存在。
3.2 配置模型构建
由以上建模过程可知,模型求解的难度随着S的增加而增大。当S较大时,稳态概率分布q难以通过直接计算得到。因此,本文研究了迭代法求解稳态概率分布q[19]。求解步骤如下:
步骤1将状态转移矩阵B进行LU分解,则分别得到下三角矩阵L和上三角矩阵U,即

步骤2 由于U是非奇异的,可将式(14)等价为

步骤3由LU=B可知,D1=M1,同时由D1E1=-CγI可得E1;
步骤4根据D2=M1+E1N,得到D2;
步骤5同理,通过依次迭代,最终得到D1,D2,…,DC+1;
步骤6令q=[x1,x2,…,xC+1],根据式(19)可得xC+1,使得xC+1DC+1=0;
步骤7由式(19)得到xCDC=xC+1N,于是计算得到xC,同理,通过降序依次迭代,最终得到稳态概率分布q=[x1,x2,…,xC+1]。
4 优化模型求解
本文优化三级特装器材库存系统的目标是在库存费用下,求得库存系统的最优库存配置方案。其中,库存费用主要包括各仓库的器材保管费用和满足需求的费用。首先,定义三级特装器材库存系统的费用结构:
Cm:需求由基层级仓库满足的费用;
Cl:需求由横向调拨满足的费用;
Cns:需求无法满足造成损失的费用;
Cc:单位时间单个备件在基层级仓库库存保管费用;
Ch:单位时间单个备件在中继级仓库库存保管费用。
三级特装器材库存系统的单位时间器材保管期望总费用为

式中
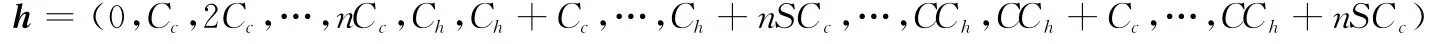
这里第i(nS+1)+(j+1)个元素表示当中继级仓库库存量为i,基层级仓库库存量为j时的库存系统单位时间器材保管期望总费用。
库存系统满足需求的期望总费用为

三级特装器材库存系统配置期望总费用为

现根据优化目标建立三级特装器材库存系统配置优化目标函数如下:

约束条件为基层级和中继级仓库的库存总量上限。
该优化模型的求解属于非线性规划问题,因此,运行Lingo软件求解较为方便,由于篇幅有限,求解过程略。
5 实例分析
特装器材库存系统对某型舰船特装器材进行供应保障,其中该库存系统的基层级由3个仓库组成,即n=3;各基层级仓库对应的器材需求率分别为λ1=3、λ2=5、λ3=8,单位为次/月;因修理厂完成器材修复对各基层级仓库产生器材补充率,均为ρσ=2件/月;中继级仓库对各基层级仓库的平均补充时间均为μ-1=1/6月;基地级仓库对中继级仓库的平均补充时间为γ-1=1/3月;库存系统运行和配置费用参数分别为Cm=20元,Cl=40元,Cns=80元,Cc=20元,Ch=10元。基地级仓库间采用随机选择转运点的策略,并结合以上参数,确定合理的特装器材配置方案。
由优化模型式(25)和式(26)得到横向调拨情况下不同库存配置方案的库存系统配置期望总费用,如图3所示。为了验证本文所建模型的有效性,将存在横向调拨情况和不存在该情况的最优配置方案进行对比。其中,由于横向调拨情况下各基层级仓库的无法满足需求概率θi均不大于0.000 4,于是要求不存在横向调拨情况下各基层级仓库的θi也满足此要求,得到两种情况下最优配置方案及总费用,如表1所示。

图3 基层级仓库总量与系统总配置费用关系

表1 两种情况下最优配置方案及费用对比结果
由对比结果可知,在相同情况下,横向调拨配置模型计算结果明显优于不考虑横向调拨的模型,前者的总配置费用仅为后者的14.55%。
为进一步分析库存配置模型各参数对结果的影响,分别对费用参数和系统运行控制参数进行调整。首先对库存系统的费用参数进行如下调整:在对单个费用参数进行调整时,其他费用参数保持不变,且调整幅度分别为原参数的-50%、-25%、+25%、+50%、+100%,得到参数变化与配置期望总费用影响关系图,如图4所示。

图4 费用参数与系统总配置费用关系
由图4可知,系统配置期望总费用随各费用参数的增加而增加,但各费用参数对配置总费用的影响程度有所不同,其中Cm和Cc对配置期望总费用的影响较大,其他费用参数的变化影响较小。尽管对各费用参数进行了调整,但得到的最优配置方案仍为(3,0,0),只是配置期望总费用不同。
最后,分析库存系统运行参数对配置结果的影响。为便于分析,初始参数将3个基层级仓库的需求率均设定为λ1=λ2=λ3=5,其余参数不变,即3个基层级仓库完全相同。由优化模型得到最优库存配置方案为(3,3,3),最优配置期望总费用为389.348元。对库存系统运行控制参数进行调整:每次仅调整一个参数,并保持其他参数不变,且调整幅度针对原参数分别为-40%、-20%、+20%、+40%。得到运行控制参数与库存系统配置期望总费用的关系图,如图5所示。
由图5可知,库存系统配置期望总费用随λ和ρσ的增加而增加,而随μ的增加而减小;库存系统最优配置方案,即基层级最优配置量随λ和μ的增加而增加,而随ρσ的增加而减少,如表2所示。同时,λ对系统配置期望总费用的影响程度最大,ρσ和μ的影响次之。

图5 系统控制参数与总配置费用关系

表2 系统控制参数灵敏度分析
对比基层级仓库间需求率不同和需求率相同的情况,可以看出,最优库存方案和最优总期望配置费用的差异较大。当需求率不同、配置量不大时,特装器材在基层级仓库储备时优先存放在需求率较低的仓库,可降低配置费用。
6 结 论
本文从舰船特装器材保障存在的问题出发,以某特装器材库存系统为研究对象,研究了该系统基层级仓库存在横向调拨和部分修复情况下的特装器材配置方法。利用Markov理论先对基层级仓库进行建模,并得到基层级仓库的稳态概率分布。其次,将基层级仓库进行整合,建立了相同器材补充率、不同基层仓库需求率的库存系统的通用配置模型,通过LU分解和迭代法得到整个库存在全部库存水平对应的稳态概率分布。最后,综合费用参数建立了该库存系统特装器材配置优化模型。通过实例分析,得到了最优配置方案,对模型的合理性和有效性进行了验证。通过对配置优化模型的参数进行调整,分析了系统运行控制参数和费用参数对最优配置方案和配置期望总费用的影响,为舰船装备保障人员、库存系统管理人员和装备机关科学制定合理的特装器材配置方案提供了决策依据和指导。
下一步将深入研究不同横向调拨策略下的配置模型构建及其对最优配置方案和配置期望总费用的影响。
[1]Zhang G Y,Li Q M,Guo X.Modeling for repairable spare parts in multi-location inventory system with lateral transshipments[J].Systems Engineering and Electronics,2012,34(7):1425- 1429.(张光宇,李庆民,郭璇.基于横向转运策略的可修备件多点库存建模方法[J].系统工程与电子技术,2012,34(7):1425- 1429.)
[2]Sherbrooke C C.Optimal inventory modeling of systems:multiechelon techniques[M].2nd ed.New York:Springer,2004.
[3]Hu J,Watson E,Schneider H.Approximate solutions for multilocation inventory systems with transshipments[J].International Journal of Production Economics,2005,97(1):31- 43.
[4]Olsson F.Optimal policies for inventory systems with lateral transshipments[J].International Journal of Production Economics,2009,118(1):175- 184.
[5]Paterson C R,Teunter K G.Enhanced lateral transshipments in a multi-location inventory system[J].European Journal of Operational Research,2012,221(2):317- 327.
[6]Hochmuth C A,Köchel P.How to order and transship in multi-location inventory systems:the simulation optimization approach[J].International Journal of Production Economics,2012,140(2):646 -654.
[7]Kukreja A,Schmidt C P.A model for lumpy demand parts in a multi-location inventory system with transshipments[J].Computers&Operations Research,2005,32(8):2059- 2075.
[8]Guan J,Liu S W,Liu J,et al.Research on two-echelon spare parts systems with lateral transshipments based on ACO[J].Journal of Air Force Engineering University(Natural Science Edition),2012,14(1):90- 94.(关娇,刘少伟,刘剑,等.基于ACO的横向供应策略两级备件库存研究[J].空军工程大学学报(自然科学版),2012,14(1):90- 94.)
[9]Fritzsche R.Cost adjustment for single item pooling models using a dynamic failure rate:a calculation for the aircraft industry[J].Transportation Research Part E:Logistics and Transportation Review,2012,48(6):1065- 1079.
[10]Paterson C,Kiesmuller G,Teunter R,et al.Inventory models with lateral transshipments:a review[J].European Journal of Operational Research,2011,210(2):125- 136.
[11]Tiacci L,Saetta S.A heuristic for balancing the inventory level of different locations through lateral shipments[J].International Journal of Production Economics,2011,131(1):87- 95.
[12]Tiacci L,Saetta S.Reducing the mean supply delay of spare parts using lateral transshipments policies[J].International Journal of Production Economics,2011,133(1):182- 191.
[13]Seidscher A,Minner S.A semi-Markov decision problem forpractive and reactive transshipments between multiple warehouses[J].European Journal of Operational Research,2013,230(1):42- 52.
[14]Wong H,Cattrysse D,Van Oudheusden D.Stocking decisions for repairable spare parts pooling in a multi-hub system[J].International Journal of Production Economics,2005,93/94:309- 317.
[15]Sheldon M R.Introduction to probability models[M].9th ed.Singapore:Elsevier,2007.
[16]Liu K.Applied Markov decision processes[M].Beijing:Tsinghua University Press,2005.(刘克.实用马尔可夫决策过程[M].北京:清华大学出版社,2005.)
[17]Tai A H,Ching W.A two-echelon model for inventory and returns[C]∥Proc.of Operations Research,2005:131- 136.
[18]Ahiska S S,Appaji S R,King R E,et al.A Markov decision process-based policy characterization approach for a stochastic inventory control problem with unreliable sourcing[J].International Journal of Production Economics,2013,144(2):485- 496.
[19]Gross D,Gu B,Soland R M.Iterative solution methods for obtaining the steady-state probability distributions of Markovian multi-echelon repairable item inventory systems[J].Computer Operation Research,1993,20(8):817- 828.
董 琪(198-6- ),男,博士研究生,主要研究方向为装备综合保障建模与仿真。
E-mail:lance0627@163.com
徐廷学(196-2- ),男,教授,博士,主要研究方向为装备综合保障理论与技术。
E-mail:xtx-yt@126.com
丛林虎(198-6- ),男,博士研究生,主要研究方向为导弹装备综合保障技术。
E-mail:342743812@qq.com
Allocation model of spare parts for three-echelon inventory system with lateral transshipment based on Markov
DONG Qi1,XU Ting-xue2,CONG Lin-hu1
(1.Graduate Students’Brigade,Naval Aeronautical and Astronautical University,Yantai 264001,China;2.Department of Ordnance Science and Technology,Naval Aeronautical and Astronautical University,Yantai 264001,China)
Focusing on the problem that there is lateral transshipment existing in the system of special equipment material,an allocation model for the three-echelon inventory system with lateral transshipment based on Markov is proposed.Combing with the condition that fault spare parts are partly restored,a subsystem inventory model for local warehouses is established according to a Markov queuing theory,and the steady state probability distribution is obtained.The allocation model for a three-echelon inventory system is established with aggregated local warehouses.Then the optimal model is established,and the objective is to minimize the total expected operating cost by choosing the maximum inventory level at the local warehouses.The iteration algorithm and Lingo software are used to solve and optimize the model.In the case,the optimal allocation cost is 14.55%of non-lateral transshipment condition,which shows that the proposed model and algorithm are rational.Finally,sensitivity analysis is made to determine the influence degree of parameters.
spare parts allocation;Markov queuing model;lateral transshipment;inventory optimization
TP 391
A
10.3969/j.issn.1001-506X.2015.11.16
1001-506X(2015)11-2524-07
2014- 12- 04;
2015- 03- 07;网络优先出版日期:2015- 07- 09。
网络优先出版地址:http://www.cnki.net/kcms/detail/11.2422.TN.20150709.1651.004.html
