基于证据理论和直觉模糊集的群决策信息集结方法

陈云翔,蔡忠义,张诤敏,项华春

(空军工程大学装备管理与安全工程学院,陕西西安710051)

基于证据理论和直觉模糊集的群决策信息集结方法

陈云翔,蔡忠义,张诤敏,项华春

(空军工程大学装备管理与安全工程学院,陕西西安710051)

针对多属性群决策信息集结问题,利用D-S证据理论和直觉模糊集的相关方法,提出基于直觉模糊熵的属性权重确定方法,并将专家对属性的直觉模糊评价信息转化为Mass函数形式,将专家关于方案集的多属性证据信息进行了修正和合成;为了便于度量任意两个专家之间评价证据的冲突程度,提出基于证据冲突度的专家权重确定方法,并将所有专家关于方案集的证据信息进行修正和综合集成。结合算例验证了方法的有效性和合理性。

多属性群决策;D-S证据合成;直觉模糊熵;证据冲突度

0 引 言

证据理论是Dempster[1]于1967年提出,后经他的学生Shafer[2]进行了推广和完善,故又称为Dempster-shafer理论(简称D-S证据理论)。D-S证据理论不需要先验概率和条件概率密度,仅依靠各种证据的积累便可不断缩小假设集。作为一种不确定性推理方法,D-S证据理论在不确定性的表示、量度和组合方面具有优势,先后推广应用于概率范围和模糊集。

直觉模糊多属性群决策问题是指通过对各方案属性评价值的综合以及各决策者给出的直觉模糊判断信息的集结,从而对备选方案进行优选与排序的过程[3-5]。针对此类问题,国内外学者提出了许多信息集结方法,如基于直觉模糊的有序加权平均(intuitionistic fuzzy ordered weighted averaging,IFOWA)算子[67]、逼近于理想解的排序方法(technique for order preference by similarity to an ideal solution, TOPSIS)[89]、基于D-S证据合成的集结方法[1013]等;但D-S证据合成规则应用于冲突证据合成时会出现有悖常理的现象。如文献[12]对专家给出的每个方案的属性值和属性权重未经修正就直接进行合成,因而忽视了这两类证据之间的潜在冲突。

基于上述考虑,本文通过对各专家给出的直觉模糊信息进行充分挖掘,利用D-S证据合成方法,提出基于证据理论的直觉模糊多属性群决策方法。首先介绍了证据理论和直觉模糊集的相关概念;然后提出了基于模糊熵的属性权重确定方法,并对考虑了属性权重的证据进行修正与合成;最后,采用融合了冲突系数和Jousselme距离的证据冲突度计算模型,求出了专家个体的权重值并对所有专家的评价证据信息进行修正和综合集成。

1 预备知识

1.1 证据理论

定义1[12]对于某一问题,人们所能认识到的可能结果称为对问题的假设。各个假设之间互斥且完备地描述了问题的所有可能,这些假设构成的集合Θ为识别框架。

定义2[12]如果集函数m:2Θ→[0,1]满足下列公式:①m(ϕ)=0,②∑A⊆Θm(A)=1,则称函数m为Θ上的基本概率分配或Mass函数。m(A)表示分配给A本身的置信测度,即支持命题A本身发生的程度。若A⊆Θ,且m(A)＞0,则称A为证据的焦元。所有焦元的集合称为核。

定义3[12]设Θ为识别框架,集函数m:2Θ→[0,1]为识别框架Θ上的Mass函数,∀A,B⊆Θ,则称由Bel(A)所定义的函数Bel:2Θ→[0,1]为Θ上的信任函数。

定理1[12](D-S合成) 设Bel1,Bel2,…,Beln为同一识别框架Θ的信任函数,m1,m2,…,mn是其对应的Mass函数,则

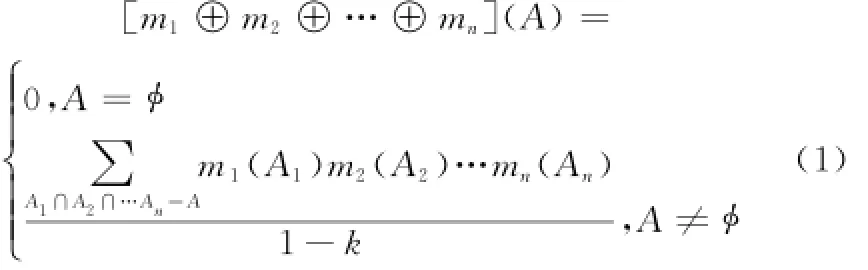
其中

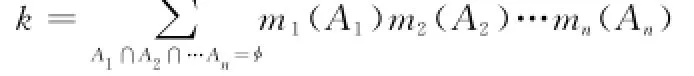
式中,“⊕”表示直和;k为证据冲突系数,1/(1-k)为归一化因子。

1.2 直觉模糊集

定义4[3]若论域X上的两个映射为μA:X→[0,1]和νA:X→[0,1],使得x∈X|→μA(x)∈[0,1]和x∈X|→νA(x)∈[0,1]并满足条件0≤μA(x)+νA(x)≤1,则称μA和νA确定了论域X上的一个直觉模糊集A,可简记为A= {〈x,μA(x),νA(x)〉|x∈X},分别称μA(x)和νA(x)为元素x属于A的隶属度和非隶属度,称πA(x)=1-μA(x)-νA(x)为元素x属于A的犹豫度。

论域X中的元素x属于A的隶属度与非隶属度所组成的有序对〈μA(x),νA(x)〉称为直觉模糊数,全体直觉模糊数的集合称为直觉模糊集,其向量形式记为A:

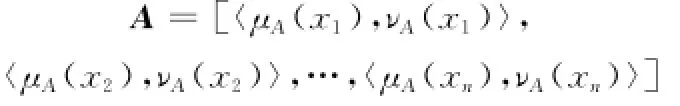
定义5[3]对于任意zij(i=1,2,…,m;j=1,2,…,n)都是直觉模糊数,则矩阵Z=(zij)m×n称为直觉模糊矩阵。

根据证据理论中Mass函数定义,直觉模糊集向量A中的直觉模糊数可表示为识别框架Θ上Mass函数,则其Mass函数mA满足以下条件:

直觉模糊集向量A中的直觉模糊数所构造出的公式(2)符合定义2中Mass函数所规定的条件。

2 属性信息集结

2.1 问题描述

现有n个可行方案xj(j=1,2,…,n)组成方案集X= {x1,x2,…,xn},由K个专家Pk(k=1,2,…,K)组成一个决策群体对每个方案关于m个属性oi(i=1,2,…,m)组成属性集O={o1,o2,…,om}进行评价。

设专家Pk对方案xj关于属性oi的评价值可表示为直觉模糊数,可得到专家Pk的直觉模糊集决策矩阵,即为

2.2 基于直觉模糊熵的属性权重确定

对于直觉模糊数a=〈μA(x),νA(x)〉,可用直觉模糊熵[14-15]来度量所蕴含信息的不确定性程度,即表示为

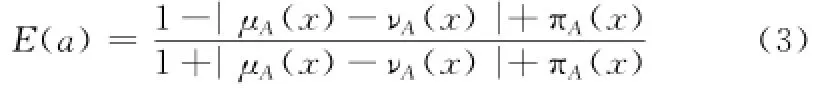
对于任意直觉模糊数aij,由式(3)可计算出该直觉模糊数的熵值,记为eij。直觉模糊熵越小,说明该直觉模糊数所蕴含信息的不确定程度越小。

专家Pk关于属性oi(i=1,2,…,m)的直觉模糊熵E为

专家Pk关于属性oi的直觉模糊熵Eik为

专家Pk关于属性oi的权重表示为

专家Pk关于属性集的权重矩阵Wk表示为

2.3 考虑属性权重的证据合成

已知专家Pk对属性oi关于方案集评价的直觉模糊向量记为dki,即

根据证据理论,可将dki看作是一条证据,其Mass函数记为mki,可表示为

式中,mk(Θ)表示识别框架(即方案集)的不确定性程度。证据dki中的直觉模糊数所构造出的公式(7)符合定义2中Mass函数所规定的条件。

由于证据合成的前提是所有证据具有同等重要程度,而现实中的证据因具有一定噪声而导致相互之间存在差异,并非同等重要。因此,在证据合成前需对参与合成的证据进行降噪和修正。

本文采用证据折扣算法[13],首先将专家Pk对属性oi关于方案集的评价证据进行修正,即

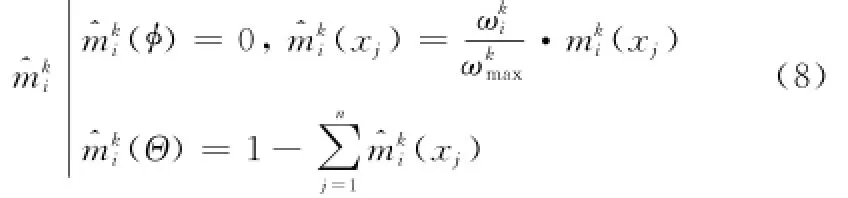
其中

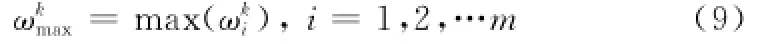
将专家Pk对属性o1,o2,…,om关于方案集的修正后的Mass函数矩阵记为Mk,即

利用D-S合成公式,将专家Pk对所有属性关于方案集修正后的评价证据进行合成,即

则专家Pk关于方案集的评价Mass函数向量记为mk,即

3 专家群决策信息集结

3.1 基于证据冲突度的专家权重确定

决策群中专家个体受自身专业背景的影响所做出的决策结果与其他专家的决策结果之间可能会存在差异和冲突,在专家赋权中应区别对待。例如,某专家提供的决策证据与其他专家之间差异较大,则该专家的意见被支持的程度应较小,赋予的权重也较小。因此,问题的核心在于如何科学确定各专家所给出的证据冲突程度。

目前常用方法有基于冲突系数的和基于Jousselme距离的证据冲突度量方法。但实践表明,只是利用冲突系数或Jousselme距离来描述和表示证据冲突都是不完善的,前者表示证据合成时不相容焦元(交集为空集)结合产生的矛盾信息大小;后者表示证据间相容焦元Mass函数之间的差异,但这两者具有一定的互补性。因此,本文提出融合了冲突系数和Jousselme距离的证据冲突计算模型[16]。

定义6[16](Jousselme距离) 设m1和m2是在识别框架Θ上的两个Mass函数,则两者之间距离可表示为

式中,m1和m2为Mass函数的向量形式的相

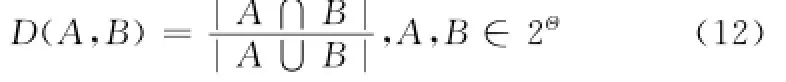
设群决策中方案集所构成的识别框架为Θ,专家Pk与Pl给出的证据之间冲突度记为cfkl,可表示为似性矩阵,其元素表示为

式中,kkl,dkl分别表示专家Pk与专家Pl提供的证据之间的冲突系数和Jousselme距离;θ为识别框架Θ上的任一假设,arg max(Bet Pm(θ))表示识别框架Θ上的最大支持

θ∈Θ假设。

由此可知,当专家Pk与专家Pl关于方案集的评价证据之间冲突最小时,cfkl=0;证据之间的冲突最大时,cfkl= 1。设专家Pk给出的评价证据被专家Pl的证据所支持程度记作spkl,则专家Pk的权重φk表示为

其中

则专家群权重矩阵Φ表示为

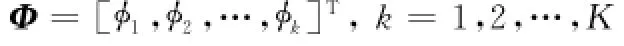
3.2 考虑专家权重的证据合成

同样,在进行证据合成前需对专家P1,P2,…,PK关于方案集的评价证据进行修正,即

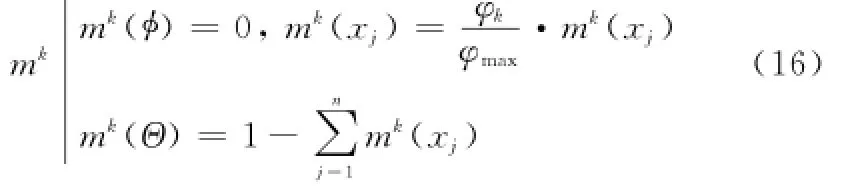
其中

同理,利用D-S合成公式,将专家P1,P2,…,PK修正后的证据进行合成,即可得到最终方案集的Mass函数向量记为m,即

4 算例分析

假设现有4个专家P1,P2,P3,P4组成一个决策群体,对某新型飞机机载设备的3个可靠性鉴定试验方案xj(j= 1,2,3)进行选优。经过分析,选择以下4个因素作为评估指标即属性:方案可行性(o1)、方案经济性(o2)、方案风险可承受性(o3)以及预期实施效果(o4)。运用专家咨询法,可得各专家Pk(k=1,2,3,4)对于属性集oi(i=1,2,3,4)的给出满意度μikj与不满意度νikj信息,具体数据见表1。

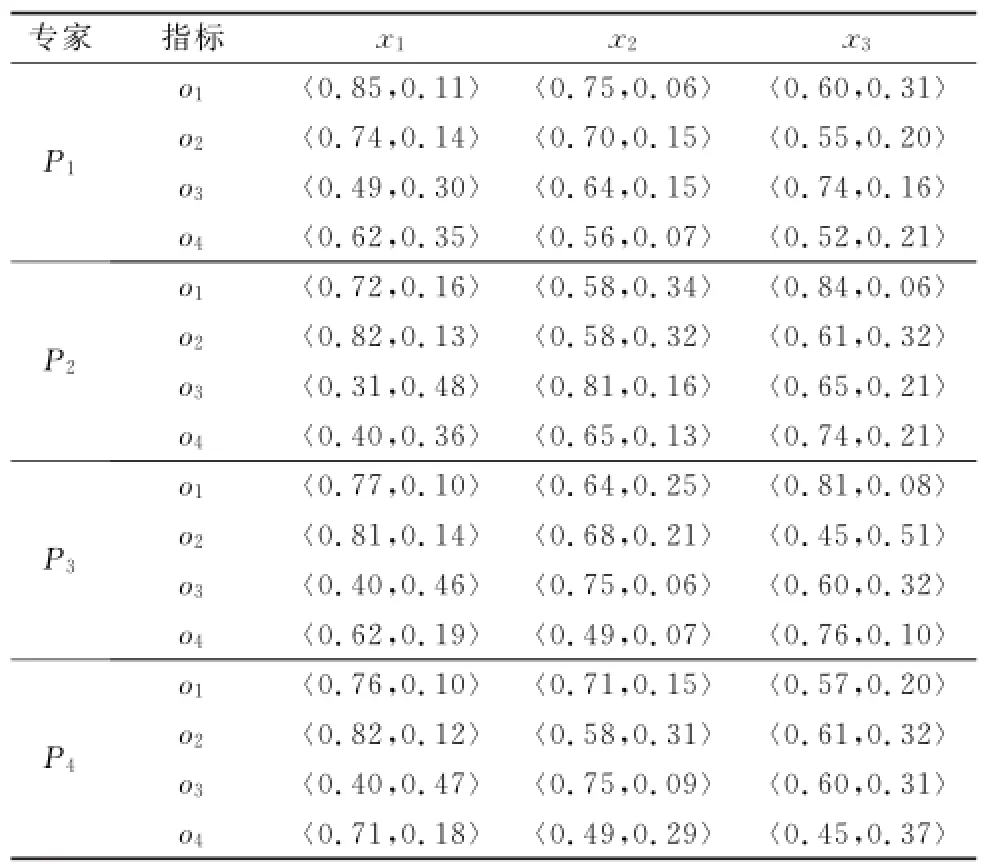
表1 专家对分配方案属性的评估

由表1可以获取专家Pk的直觉模糊集决策矩阵Dk;由式(5)和式(6)确定专家Pk关于属性集O的权重矩阵Wk为

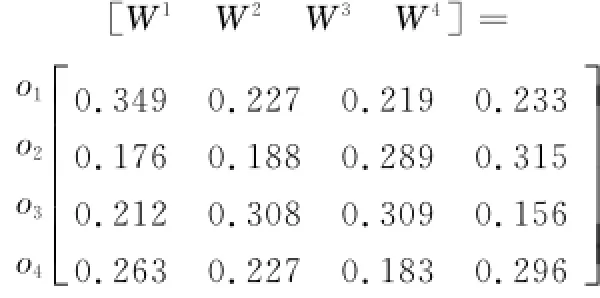
由式(7)～式(10)得到专家Pk关于方案集的评价Mass函数向量记为mk,即

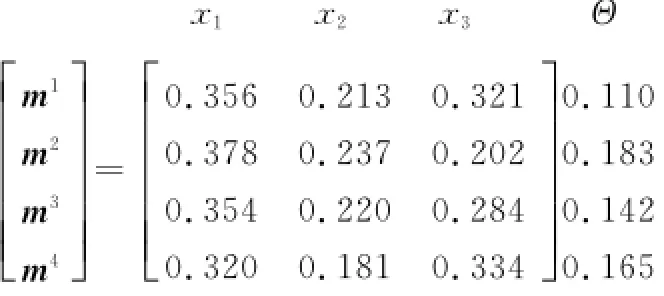
由式(13)计算出两两专家之间关于方案集的评价证据的冲突度cfkl。

由式(14)和式(15)得到专家群权重矩阵Φ。

由式(16)和式(17)对专家P1,P2,…,PK关于方案集的评价证据进行修正,再运用D-S证据合成得到最终方案集的Mass函数向量记为m。

因此,可靠性鉴定试验备选方案的优劣排序为x1＞x3＞x2,且x1为最满意的方案。

5 结 论

针对直觉模糊信息环境下的多属性群决策问题,在属性权重和专家权重均未知的情况下,本文综合运用D-S证据理论和直觉模糊集的相关概念,提出了基于模糊熵的属性权重确定方法和基于证据冲突度的专家权重确定方法,分别对考虑了属性权重和专家权重的相关证据进行修正与合成,从而实现了对专家群决策信息的综合集成。结合算例验证了方法的有效性和合理性,给出了备选方案的优劣排序。

[1]Dempster A P.Upper and lower probabilities induced by a multivalued mapping[J].Annuals of Mathematical Statistics,1967, 38(4):325-339.

[2]Shafer G.A mathematical theory of evidence[M].Princeton: Princeton University Press,1976.

[3]Li D F.Intuitionistic fuzzy set decision and game analysis methodologies[M].Beijing:National Defense Industry Press,2012:21-34.(李登峰.直觉模糊集决策与对策分析方法[M].北京:国防工业出版社,2012:21-34.)

[4]Wei G W.Gray relational analysis method for intuitionistic fuzzy multiple attribute decision making[J].Ex pert Systems with Applications,2011,38(9):11671-11677.

[5]Geng T,Zhang A,Lu G S.Consensus intuitionistic fuzzy group decision-making method for aircraft cockpit display and control system evaluation[J].Journal of Systems Engineering and Electronics,2013,24(4):634-641.

[6]Zhou S M,Francisco C,John R I,et al.Fuzzification of the OWA operators for aggregating uncertain information with uncertain weights[J].Theory and Practice Studies in Fuzziness and Soft Computing,2011,26(5):91-109

[7]Zhao H,Xu Z S,Ni M F,et al.Generalized aggregation operators for intuitionistic fuzzy sets[J].International Journal of Intelligent Systems,2010,25(1):1-30.

[8]Socorro M,Garcia C.The TOPSIS method and its application to linguistic variables[J].Preference and Decisions,2010,25(7): 383-395.

[9]Tian M,He Y Y,Liu S F.Extension of TOPSIS for fuzzy multi-attribute decision making problem based on experimental analysis[J].Journal of Systems Engineering and Electronics, 2010,21(3):216-222.

[10]Guo J,Song J S,Yang M,et al.Recovery importance decision making for multi-missions based on Dempster-Shafer theory[J]. Systems Engineering and Electronics,2011,33(3):581-584. (郭军,宋建社,杨檬,等.基于证据理论的多任务抢修重要度决策[J].系统工程与电子技术,2011,33(3):581-584.)

[11]Dymova L,Sevastjanoc P.An interpretation of intuitionistic fuzzy sets in terms of evidence theory:decision making aspect[J]. Knowledge-Based Systems,2010,23(8):772-782.

[12]Jiang H L,He J M,Zhuang Y M,et al.Approach to group decision making based on intuitionistic fuzzy sets and evidence theory[J].Control and Decision,2012,27(5):752-756. (江红莉,何建敏,庄亚明,等.基于直觉模糊集和证据理论的群决策方法[J].控制与决策,2012,27(5):752-756.)

[13]Shi C,Cheng Y M,Pan Q.Method to aggregate hybrid preference information based on intuitionistic fuzzy and evidence theory[J].Control and Decision,2012,27(8):1163-1168.(史超,程咏梅,潘泉.基于直觉模糊和证据理论的混合型偏好信息集结方法[J].控制与决策,2012,27(8):1163-1168.)

[14]Szmidt E,Kacprzyk J.Entropy for intuitionistic fuzzy sets[J]. Fuzzy Sets and Systems,2001,118(3):467-477.

[15]Wu J Z,Zhang Q.Multicriteria decision making method based on intuitionistic fuzzy weighted entropy[J].Ex pert Systems with Applications,2011,38(3):916 922.

[16]Jousselme A L,Grenier D,Bosse E.A new distance between two bodies of evidence[J].Information Fusion,2001,2(1):91 -101.

蔡忠义(1988-),通信作者,男,博士研究生,主要研究方向为装备可靠性与系统工程。

E-mail:afeuczy@163.com

张诤敏(1964-),女,教授,硕士,主要研究方向为装备系统工程。

E-mail:646297491@qq.com

项华春(1980-),男,副教授,博士,主要研究方向为装备可靠性与系统工程。

E-mail:xhc09260926@163.com

Method for group decision-making information integration based on evidence theory and intuitionistic fuzzy set

CHEN Yun-xiang,CAI Zhong-yi,ZHANG Zheng-min,XIANG Hua-chun
(Equipment Management&Safety Engineering College,Air Force Engineering University,Xi’an 710051,China)

For information integration of multi-attribute group decision-making,the paper uses the Dempster-Shafer(D-S)evidence theory and relevant theories of the intuitionistic fuzzy set,puts forward a method for attribution-weight determination based on intuitionistic fuzzy entropy,turns the intuitionistic fuzzy evaluation information of the attribute into the Mass function form,and modifies and synthesizes the multi-attribute of the expert group towards the project set.In order to get the conflict degree of two experts’evaluation evidence,the paper puts forward a method for expert-weight determination based on the evidence conflict degree,and modifies and integrates the evidence information of all experts towards the project set.An example is used to verify the effectiveness and rationality of this method.

group decision-making of multi-attribute;D-S evidence synthesization;intuitionistic fuzzy entropy;evidence conflict degree

C 93

A

10.3969/j.issn.1001-506X.2015.03.19

陈云翔(1962-),男,教授,博士,主要研究方向为装备管理与决策、装备维修保障。

E-mail:cyx87793@163.com

2014 03 04;

2014 07 01;网络优先出版日期:2014 10 19。

网络优先出版地址:http://w ww.cnki.net/kcms/detail/11.2422.TN.20141019.2344.003.html

总装“十二五”国防预先研究项目资助课题