基于B样条空间等距线的机器人轨迹优化算法
2015-06-05胡绳荪庹宇鲲申俊琦陈昌亮
胡绳荪,庹宇鲲,申俊琦,陈昌亮,谷 文,李 坚
(1. 天津大学天津市现代连接技术重点实验室,天津 300072;2. 天津大学材料科学与工程学院,天津 300072;3. 天津职业技术师范大学天津市高速切削与精密加工重点实验室,天津 300222;4. 中国第一重型机械集团核电石化事业部,大连 116113)
基于B样条空间等距线的机器人轨迹优化算法
胡绳荪1,2,庹宇鲲1,2,申俊琦1,2,陈昌亮3,谷 文4,李 坚4
(1. 天津大学天津市现代连接技术重点实验室,天津 300072;2. 天津大学材料科学与工程学院,天津 300072;
3. 天津职业技术师范大学天津市高速切削与精密加工重点实验室,天津 300222;4. 中国第一重型机械集团核电石化事业部,大连 116113)
针对J形坡口焊接机器人轨迹示教中理论轨迹与实际轨迹偏差较大的问题,利用实际轨迹的空间等距线逼近下一道焊接轨迹,并设计了相贯线轨迹等距线的B样条逼近算法. 算法主要包括:基于等曲线弧长准则对原B样条曲线取样;利用向心算法计算取样点的等距点;计算插值于该等距点的3次B样条曲线;在给定的全局误差限内去除多余控制顶点. 试验结果表明:等距点的向心算法可以有效解决相贯线曲线局部修改后主法向量发散的问题;全局插值方法可以保留原曲线修改特征;全局误差限下去除多余控制顶点可以减少B样条曲线控制顶点数目.
J形坡口;球管相贯线;B样条;等距线;逼近
焊接作为核电设备制造的关键技术之一,不仅关系到核电站建造的质量与安全,而且明显影响核电站建造的调度与周期[1]. 针对核电压力容器封头与圆管相贯形成的J形坡口焊接特点,建立了其自动化焊接设备及相贯线轨迹数学模型[2-3]. 而由于工件的装配误差等影响,J形坡口焊接机器人在焊前需要操作人员对相贯线轨迹进行局部修改[4],其修改过程比较耗时. 虽然理论轨迹与实际轨迹偏差较大,但试验表明,相邻两道焊接轨迹的修改特征相似. 因此可以利用当前焊接轨迹的等距线逼近下一道焊接轨迹,从而保留当前道焊接轨迹的修改特征,减少下一道轨迹的修改点数目,进而提高焊接效率.
等距线在很多工业领域都有重要应用,如数控切削轨迹生成、机器人路径规划、铁路设计等[5]. 由于自由曲线的等距线不存在封闭解,故通常使用低阶样条曲线对离散等距点进行插值,进而逼近等距线[6-7].但是当取样点分布不均匀或等距点的计算存在误差时,利用插值方法将产生较大误差. 而利用逼近算法求取等距线不仅可以降低取样点的噪声对等距线的影响,而且可以获得较少的控制顶点[8-10].
现有等距线算法多集中于平面等距线,对空间等距线的研究较少. 为此,笔者针对J形坡口焊接轨迹特点,研究了其空间等距线的逼近算法.
1 空间B样条曲线等距点
给定一条B样条曲线C(u),
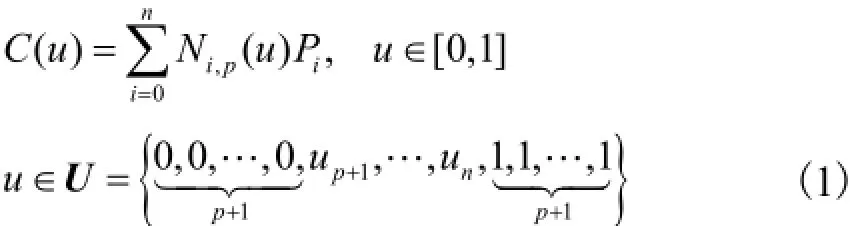
式中:Ni,p(u)为B样条基函数;p为该B样条曲线的阶次;U为节点向量;Pi为控制顶点.该B样条曲线的等距线定义为
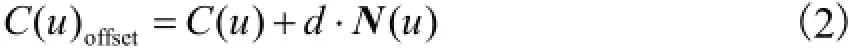
式中:N(u)为参数为u时曲线的单位法向量;d为等距量;C(u)offset为C(u)的等距线.
1.1 空间B样条曲线等距点向心算法
平面曲线的等距点可以直接根据式(2)求解,但空间曲线等距点的求解更为复杂.图1(a)为对相贯线的B样条逼近曲线进行局部修改后曲线上各点的主法向量示意,局部修改点的引入将使修改点附近各点的主法向量发散.若沿着该方向计算等距点将使等距线产生较大波动.
本文利用向心算法计算空间曲线等距点.给定J形坡口相贯线轨迹参数方程,首先计算相贯线的中心点Mc,

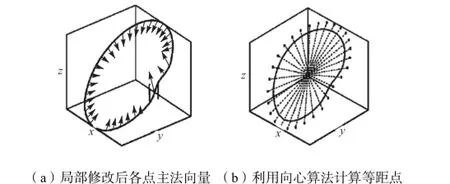
图1 等距点算法比较Fig.1 Comparison of offset points calculation algorithms
式中:Mi为相贯点坐标;Mc为中心点坐标;n+1为相贯点数量.则等距点的计算式为
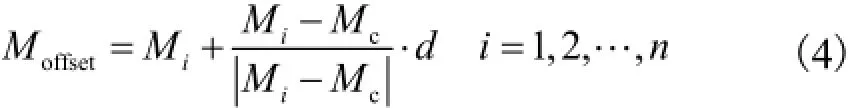
式中:Moffset为等距点坐标;|Mi-Mc|为相贯点与中心点距离.利用向心算法,对图1(a)相贯线轨迹求取等距点,结果如图1(b)所示,图中黑色球体即等距点.该算法可以避免空间曲线主法向量发散问题,即使对相贯线进行局部修改,等距点也能保持原曲线特征.
1.2 基于等曲线弧长的等距点采样
等距点数量及采样方法对等距线形状及算法效率有重要影响.过多采样点将降低算法效率,而过少采样点无法保留曲线修改特征.一般而言,对曲线的平滑区域稀疏采样,局部修改区域密集采样可以在曲线形状和算法效率上取得很好的平衡.
与基于二阶导数的采样准则[9]相比,基于等曲线弧长的采样方法计算量很小.而且由于曲线在修改点附近曲率较大,相对于未进行局部修改的区域,利用等曲线弧长准则将在相同弦长内对曲线进行更为密集的采样,这有利于保存曲线的修改特征.该采样准则的计算式为
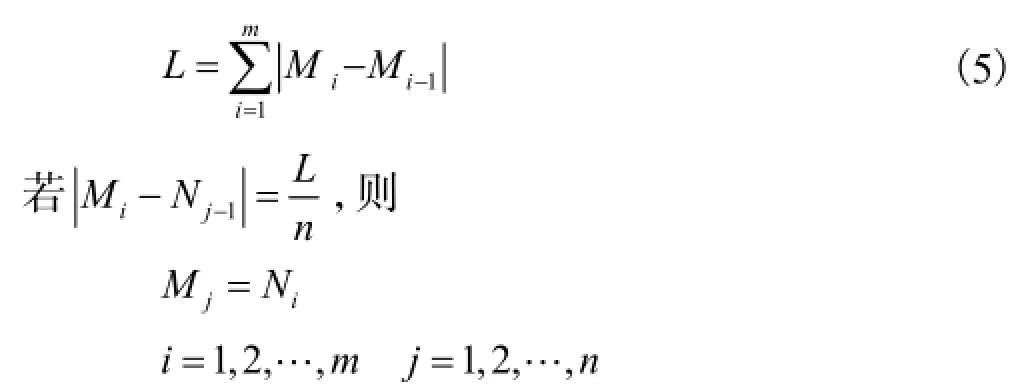
式中:L为原曲线总弧长;Ni为相贯点;Mj为采样点;m+1为采样点数目.
2 基于最少控制顶点的B样条曲线逼近
2.1 全局插值
对于曲线拟合问题,普遍采用的是插值或逼近的算法.插值算法计算速度快,而且保证插值曲线经过数据点,但数据点的噪声会给曲线带来误差.逼近算法计算量大,但对数据点的噪声有很好的鲁棒性,并且可以在限定条件下去除部分控制顶点,使曲线的形式更为简单.每个核电压力容器封头上需要安插数十个圆管,每个圆管与封头的连接需要数十条焊道,每条焊道轨迹都要存入数据库,若能减少每条轨迹的控制顶点数量,则所需存储容量将大大减小.
如果对密集采样得到的等距点进行全局插值将产生大量控制顶点,本文采用固定全局误差限下最少控制顶点的逼近算法来去除冗余的控制顶点.通过与全局插值和固定控制顶点数目的逼近算法比较,该算法在控制顶点数量、逼近精度以及算法效率上均有很好的效果,算法流程如图2所示.
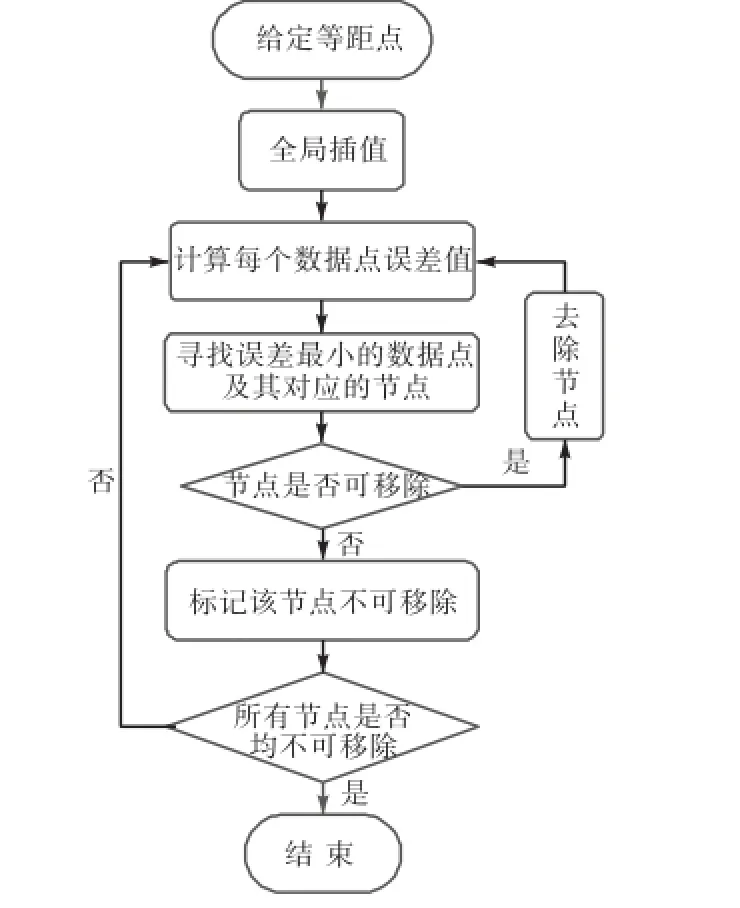
图2 节点去除算法流程Fig.2 Flowchart of knot removal algorithm
图3 为对101个等距点进行3次B样条全局插值的效果图,图中曲线为插值得到的B样条曲线,球体为控制顶点.
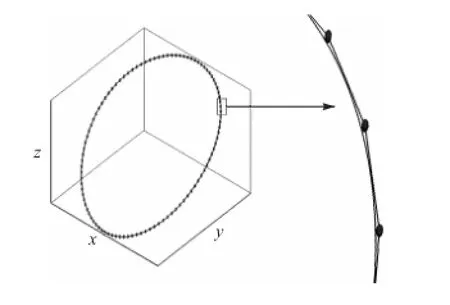
图3 全局插值Fig.3 Global interpolation
2.2 去除多余节点
去除多余节点需要计算去除节点后新的控制顶点坐标.给定节点向量U,若去除某一节点u一次,当且仅当曲线在该节点的连续性高于Cp-s时,消除该节点不会改变曲线形状,否则消除该节点将改变曲线在节点u附近的形状,其中s为该节点重复次数. 去除该节点后新的控制顶点[11]为
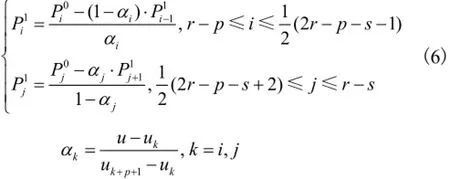
式中:P0为原控制顶点;P1为消去节点u一次后的控制顶点;r为消去节点下标. 去除节点后,新曲线误差限[12]为
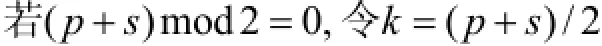
则
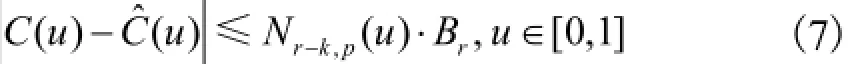
其中

式中ˆ()C u为去除节点后曲线各点坐标. 以去除节点后等距点的误差作为该节点是否可被去除的判据,因此需要计算等距点在B样条曲线上的投影. 在p≤4条件下,等距点的投影可用解析形式精确求解,求解的步骤[12]如下:
(1) 利用B样条曲线的强凸包性确定可能包含数据点Qk投影的候选C(u)段;
(2) 利用节点插入,提取出各候选段,并将其转化为Bezier曲线形式;
(3) 对每一段Bezier曲线,列出包含一个未知数的3个多项式方程,若这3个方程具有一个共同的解,则Qk位于这一段上.
求出每个等距点的投影坐标后便可以根据式(7)和式(8)求出去除某一节点后每个等距点的误差值.进而求取曲线的最大模偏差,即

最大模偏差对应的节点便是待删除的节点. 若最大模偏差小于全局误差值,表明该节点及对应的控制顶点可以删除,否则该节点不可删除.
图4为对图3曲线进行节点去除的结果,在全局误差限为0.5,mm条件下,曲线的控制顶点由101个降低到18个.
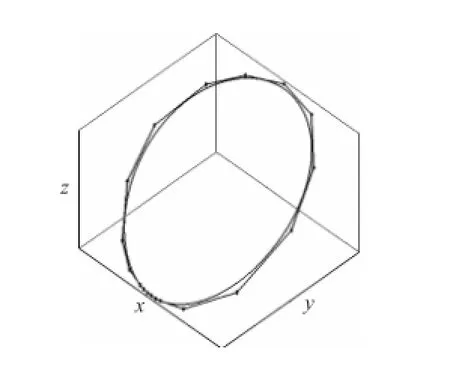
图4 节点去除曲线Fig.4 Spline after knot removed
3 结果分析及比较
利用基于等曲线弧长的取样准则对原曲线密集取样,利用向心算法计算取样点的等距点,对等距点进行全局插值并在全局误差限内去除多余控制顶点,最终等距线如图5所示.
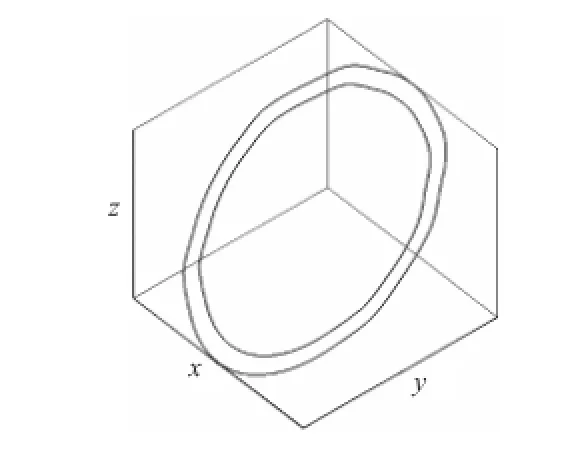
图5 等距线效果Fig.5 Renderings of offset splines
表1为对101个相贯点利用不同拟合方法进行曲线拟合的参数对比. 为比较不同拟合方法的效果,首先计算201个相贯点,将奇数下标的101个相贯点用于曲线拟合,偶数下标的100个相贯点用于计算拟合参数. 拟合参数中最大误差为100个相贯点与拟合曲线的投影误差最大值,全局误差和为100个相贯点与拟合曲线投影误差和. 固定控制顶点数量逼近方法的控制顶点数设为18,固定全局误差限逼近方法的全局误差限设为0.5,mm.
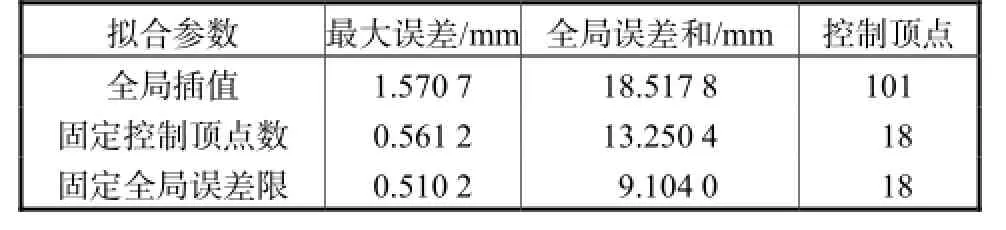
表1 不同拟合方法的拟合参数Tab.1 Fitting parameters of different fitting methods
可以看出,固定全局误差限的逼近方法在全局误差值和控制顶点数目上相对全局插值和固定控制顶点数量的全局逼近方法有很好的平衡.
全局插值方法虽然保证曲线经过数据点,但无法保证数据点间曲线的拟合效果,尤其在数据点存在噪声条件下,数据点之间曲线的误差很大. 固定控制顶点数量的全局逼近方法虽然在最大误差和全局误差和与固定全局误差限的逼近方法有相似的表现,但是在缺乏一定先验知识的条件下很难指定合理的控制顶点数量,而且其最大误差值难以保证.相对控制顶点数量而言,全局误差限是更合理的限定条件.
表2为数据点数量为101时,在不同全局误差限下对数据点进行逼近得到的B样条曲线控制顶点数量. 为了保持原曲线的修改特征,局部修改点的引入将增加控制顶点数量,误差限的增大将减少控制顶点数量. 但在不同的全局误差限下,控制顶点数量相对全局插值B样条曲线控制顶点数量都有大幅度降低.
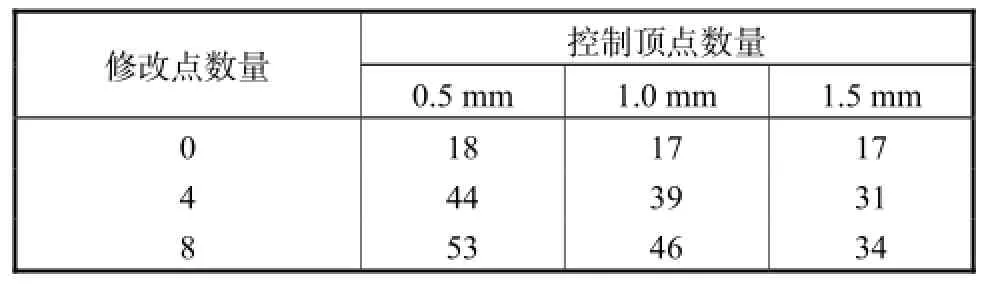
表2 不同全局误差限下控制顶点数量Tab.2Number of control points under different global error bounds
图6为理论轨迹与实际轨迹以及等距线轨迹与实际轨迹局部细节对比. 由于等距线保留了前一道焊接轨迹的修改特征,所以等距线轨迹更贴合实际轨迹,逼近效果优于理论轨迹.
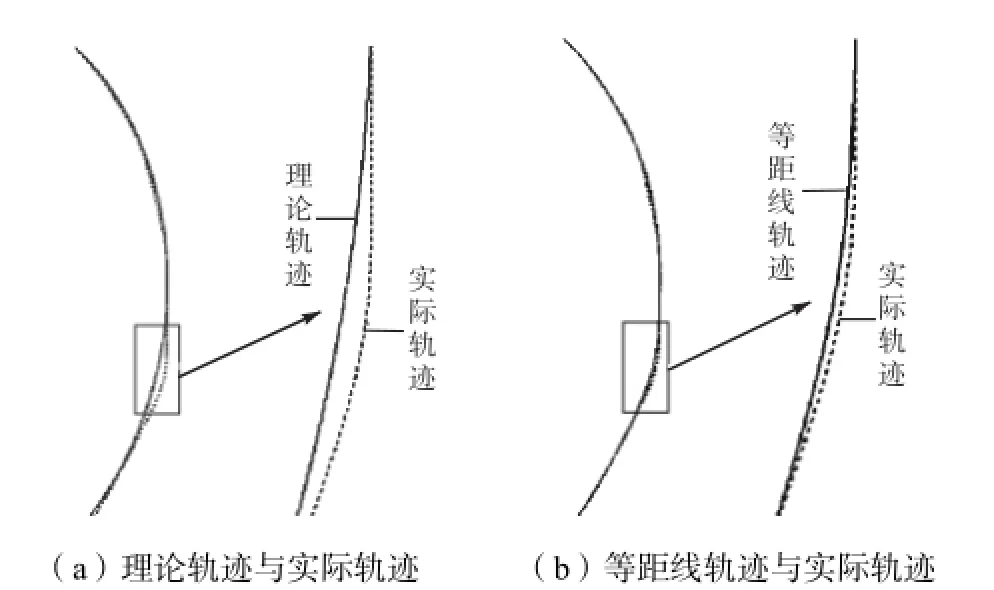
图6 理论轨迹和等距线轨迹与实际轨迹的比较Fig.6Comparison of theoretical trajectory and offset trajectory with real trajectory
在对前一道焊接轨迹进行示教时,共插入23个修改点,记录修改点坐标及其相对起始点的旋转角度,并分别利用理论轨迹和等距线逼近下一道焊接轨迹. 在与前一道轨迹修改点旋转角度相同的位置计算理论轨迹点、等距线轨迹点和实际轨迹点的坐标,部分坐标如表3所示.
计算理论轨迹和等距线轨迹相对于实际轨迹的投影误差得出:理论轨迹相对实际轨迹的投影误差和为13.92,mm,等距线轨迹相对于实际轨迹的投影误差和为4.68,mm.

表3 实际轨迹、理论轨迹与等距线轨迹部分数据点Tab.3 Part of data points on the real trajectory,theoretical trajectory and offset trajectory
4 结 论
(1) 利用等距点的向心算法,可以解决空间曲线主法向量发散问题,利用等曲线弧长准则对原曲线进行密集采样可以保证算法效率,同时保留原曲线的修改特征.
(2) 采用固定全局误差限的方法去除多余控制顶点,可以降低等距点噪声对等距线的影响,同时减少曲线的控制顶点数量,该方法可在曲线的控制顶点数目以及全局误差方面有很好的效果.
(3) 试验表明,相比理论计算相贯线轨迹,利用等距线逼近J形坡口相贯线轨迹能够大幅度降低轨迹的全局误差和,提高机器人轨迹示教效率.
[1] 冯英超,石爱强,王 挺,等. 核电站安装施工中自动化焊接技术应用分析[J]. 电焊机,2009,39(8): 27-29.
Feng Yingchao,Shi Aiqiang,Wang Ting,et al. Application and analysis of automatic welding technology in nuclear power plant construction [J]. Electric Welding Machine,2009,39(8):27-29(in Chinese).
[2] Chen C L,Hu S S,He D L,et al. Kinematic analysis and trajectory planning of J-groove welding robot [J]. Transactions of Tianjin University,2012,18(5):350-356.
[3] 胡绳荪,王明建,申俊琦,等. J形坡口焊接机器人运动控制系统设计[J]. 天津大学学报:自然科学与工程技术版,2014,47(4):371-376.
Hu Shengsun,Wang Mingjian,Shen Junqi,et al. Design of J-groove welding robot motion control system[J]. Journal of Tianjin University:Science and Technology,2014,47(4):371-376(in Chinese).
[4] Chen C L,Hu S S,He D L,et al. An approach to the path planning of tube-sphere intersection welds with the robot dedicated to J-groove joints[J]. Robotics and Computer-Integrated Manufacturing,2013,29(4):41-48.
[5] Maekawa T. An overview of offset curves and surfaces [J]. Computer-Aided Design,1999,31(3):165-173.
[6] Klass R. An offset spline approximation for plane cubic splines [J]. Computer-Aided Design,1983,15(5): 297-299.
[7] Pham B. Offset approximation of uniform B-splines [J]. Computer-Aided Design,1988,20(8):471-474.
[8] Piegl L A,Tiller W. Computing offsets of NURBS curves and surfaces [J]. Computer-Aided Design, 1999,31(2):147-156.
[9] Xu Xiduo,Li Jijun,Zheng Hong. A new NURBS offset curves and surfaces algorithm based on different geometry shape [C]// IEEE 10th International Conference on Computer-Aided Industrial Design & Conceptual Design. Wenzhou,China,2009:2384-2390.
[10] Khan M A,Chen Z C. Approximation of planar offset curves with globally bounded error for B-spline NC tool paths [J]. International Journal of Production Research,2012,50(23):6811-6825.
[11] Piegl L A,Tiller W. The NURBS Book[M]. 2nd ed. New York:Springer-Verlag,1997.
[12] Tiller W. Knot-removal algorithms for NURBS curves and surfaces [J]. Computer-Aided Design,1992, 24(8):445-453.
(责任编辑:田 军)
Robot Trajectory Optimization Algorithm Based on Spatial Offset B-Spline
Hu Shengsun1,2,Tuo Yukun1,2,Shen Junqi1,2,Chen Changliang3,Gu Wen4,Li Jian4
(1. Tianjin Key Laboratory of Advanced Joining Technology,Tianjin University,Tianjin 300072,China;2. School of Materials Science and Engineering,Tianjin University,Tianjin 300072,China;3. Tianjin Key Laboratory of High Speed Cutting and Precision Machining,Tianjin University of Technology and Education,Tianjin 300222,China;4. Nuclear Power and Petro-Chemical Business Group,China First Heavy Industries,Dalian 116113,China)
For the problem of the large deviation between the theoretical trajectory and the real trajectory of the J-groove joint welding robot during trajectory teaching, a solution is proposed using the offset spline of the real trajectory to approximate the next welding trajectory. An approximation algorithm for offset B-spline of intersecting splines is designed, which includes the following steps: sampling the original B-spline with the uniform curve arc length criterion; calculating the offset points of the sample points with the centripetal algorithm; fitting a cubic B-spline with global interpolation; removing most control points under the global error bound. The experimental results are as follows: the centripetal algorithm could solve the problem of the divergence of the principal normal vectors after local modification on the intersecting curve; the algorithm of global interpolating could retain the modification features of the original trajectory; the algorithm of removing control points under global error bound could remove most control points effectively and reduce the number of control points of B-spline.
J-groove joints;sphere-tube intersecting line;B-spline;offset spline;approximation
TG409
A
0493-2137(2015)08-0723-05
10.11784/tdxbz201404089
2014-04-22;
2014-05-20.
国家自然科学基金资助项目(50975195);天津市应用基础及前沿技术研究计划资助项目(10JCYBJC06500).
胡绳荪(1956— ),男,教授,huss@tju.edu.cn.
申俊琦,shenjunqi@tju.edu.cn.
时间:2014-09-16.
http://www.cnki.net/kcms/doi/10.11784/tdxbz201404089.html.
