团泊洼-沙井子行洪道洪水演进数学模型的研究与应用
2015-06-05李大鸣杨紫佩赵明雨
李大鸣,杨紫佩,赵明雨,王 笑
(天津大学水利工程仿真与安全国家重点实验室,天津 300072)
团泊洼-沙井子行洪道洪水演进数学模型的研究与应用
李大鸣,杨紫佩,赵明雨,王 笑
(天津大学水利工程仿真与安全国家重点实验室,天津 300072)
以二维非恒定流基本控制方程为理论基础,采用有限体积法,建立了洪水演进数学模型.根据团泊洼蓄滞洪区的实际地形、地貌,采用该模型模拟了“56”型洪水分洪流量过程,对水量、最大流量和淹没水位进行了验证,其结果与设计结果吻合较好.应用该模型对团泊洼安全区塔基建设工程前后进行了洪水演进模拟,并通过构建塔基局部加密模型,分析了塔基建设前后对局部行洪、附近水深、流速的影响,为蓄滞洪区的工程建设提供了研究依据.
蓄滞洪区;团泊洼;洪水演进;数学模型
蓄滞洪区是流域防洪体系不可或缺的重要设施,可以有效地蓄滞超标准洪水,减轻下游重点地区的防洪压力,在我国防洪体系中具有非常重要的作用.
研究模拟蓄滞洪区内洪水运动情况的方法有很多,其中数值模拟的方法可以获得蓄滞洪区内各处的水位、水深和流速等信息,能够为防洪决策提供支持,尽可能减少洪灾损失[1].对洪水演进的模拟,国内外的专家进行了不少研究.Cunge[2]应用改进的马斯京根方法模拟河道洪水演进.Akanbi等[3]使用有限元法模拟洪水波在干河床上的演进.Caleffi 等[4]采用二维浅水方程对Toce河的洪水演进进行了模拟.刘树坤等[5]用有结构网格对小清河分洪区洪水演进进行了模拟.张艳霞等[6]基于汉江与长江两江洪水演进特点建立了两江洪水演进数学模型.谢作涛等[7]从求解一维对流方程的Holly-Preissmann格式出发,结合有限差分法建立了一维洪水演进数学模型.王晓玲等[8]采用有限差分法建立了二维洪水演进数学模型,模拟复杂河网中分洪后水流在较大平面范围内的流动情况.张细兵等[9]基于非结构三角形网格,采用有限体积算法,建立了分蓄洪区水沙演进数学模型.王船海等[10]用有限体积法对行蓄洪区洪水演进进行了研究.周孝德等[11]用二维洪水演进的隐式差分模型,对君山滞洪区进行洪水演进的模拟计算.谢作涛等[7]、刘树坤等[5]采用的有限差分法是以结点为基础,构造差分和导数之间的关系,保证解在结点处的连续光滑,其所适用的边界规整,局部加密较困难;Akanbi等[3]应用了有限元的方法,有限元以单元近似为基础,通过单元积分构造函数与导数之间的关系,用插值函数近似连续函数的解,保证了解在单元上的连续和光滑,能适应复杂边界要求,局部加密方便灵活,但守恒上存在一定缺陷.有限体积法得出的离散方程,要求因变量的积分守恒对任意一组控制体积都能得到满足,进而满足对整个计算区域的控制,守恒性较好,因此李大鸣等[12-13]采用有限体积法建立了一维河道嵌套于平面二维蓄滞洪区的洪水演进水流数学模型,为复杂地形或具有多个分洪口门的蓄滞洪区洪水调度提供了一定的理论参考.
本文以二维非恒定流方程为基本理论,采用有限体积法对二维非恒定流基本控制方程进行离散求解.采用天津团泊洼蓄滞洪区安全区规划前的洪水设计成果进行了比较验证;对电塔基座局部进行了加密构建,并给出了整个加密区工程前后流速变化差值和水位的壅高量等值线分布图;在塔基位置附近选择具有代表性的特征点,对加密模型区域中各方案工程建设前后最大水深、最大流速、最大壅水高度进行了统计比较.
1 数学模型基本理论
1.1 二维非恒定流基本方程
连续方程

式中:H为水深;t为时间;z为水位,z=z0+H,z0为底高程;q为源汇项;M、N分别为x、y方向上的单宽流量,M=Hu,N=Hv,u、v分别为x、y方向的平均流速;n为糙率;g为重力加速度.
1.2 有限体积离散
按照有限体积法布置二维网格的方式如图1所示.它取单元网格为控制体,在网格中心处计算水位z,在网格周边通道的中点处计算流量Q.中点的通量可用中心格式(如取相邻两格形心处通量的平均)或逆风格式确定.则将式(1)改写成矢量形式,按照有限体积法,将其在控制体内进行积分,对水位H和流量Q按时间交错方式进行计算(见图2),则式(1)可离散为

式中:Ai为第i个网格的单元面积;Lik为i号网格的第k号通道的长度;Qik为i号网格的第k号通道的单宽流量;为第i个网格在T+Δt时刻的抽排水量,T为起算时刻,Δt为时间增量.

图1 水位z和流量Q的空间布置方式Fig.1 Space arrangement plan of water level H and flow Q

图2 水位z和流量Q的时间交错计算方式Fig.2 Time arrangement plan of water level H and flow Q
1.3 数值通量计算
通量计算是有限体积算法的关键,为得到较好的计算结果,常采用各类高性能格式以提高计算精度.考虑到滞洪区内各种地形条件及铁路、公路等建筑物情况,本模型将所有单元间的通道按不同情况进行分类,概化为地面型通道、河道型通道、特殊通道和连续堤或缺口堤通道4类进行处理,并给所有通道附加特征信息,以相应的水力学公式进行通量计算[14].
(1)地面型通道,即通道两侧单元为陆地地面,且通道上没有堤防等阻水建筑物.考虑到滞洪区内的地形起伏不大,地面洪水演进主要受到重力和阻力的作用,忽略掉加速度项,即只保留式(2)和(3)中的,利用
差分方法离散得到地面型通道的动量离散方程

(2)河道型通道,即通道两侧网格均为河道型网格,动量方程中保留局地加速度项、重力项和阻力项,即保留式(2)和(3)中的利用差分方法离散得到河道型通道的动量离散方程

(3)对于滞洪区内宽度较小的河流,不便于将其划分成独立的单元网格,也不能忽略不计,为了方便计算,模型中将其模拟成具有高度和长宽尺寸的特殊通道,以反映水流沿河而流以及河道与两侧陆地之间水量交换的现象.如果通道两侧有阻水建筑物,可以将其设为堤防.
2 洪水演进数学模型的建立
2.1 团泊洼和沙井子滞洪情况简介
团泊洼蓄滞洪区与沙井子行洪道均属于大清河水系,二者在海河流域防洪体系中具有重要作用.其中团泊洼滞洪区是海河流域7大蓄滞洪区之一,沙井子行洪道是大清河超标准洪水的滞洪区,是保护天津市区、津浦铁路以及京沪高速公路等重要设施防洪安全必不可少的行蓄洪工程.在东淀、贾口洼、文安洼相继运用后,西三洼滞洪水位继续上涨至威胁津浦铁路及天津市区安全时,须利用25孔桥向团泊洼分洪并经沙井子行洪道导洪入海.团泊洼、沙井子经历了1963年洪水的滞洪运用,也是新中国成立以来的唯一一次滞洪运用.
2.2 网格的剖分
模型基本网格采用1,km×1,km网格,考虑铁路、公路和水库的曲线和不规则轮廓将网格划分为任意形状,生成网格结点2,698个,网格单元2,470个,网格通道5,163个,模型计算范围覆盖面积约1,914,km2,图3中红线为塔基建设路线,箭头为水流方向.模型中村庄以地形高度和糙率变化来表现,公路、堤坝和河道以通道高程变化来表现.

图3 团泊洼模型网格剖分Fig.3 Grid subdivision of Tuanbowa model
2.3 模型边界条件
整体模型上边界为团泊洼南运河东侧京浦铁路25孔桥分洪口门,边界流量过程采用《天津团泊洼蓄滞洪区建设与管理规划报告》中的设计“56”型洪水分洪流量过程,由于流量过程数据缺失,采用最大流量和总水量拟合给出.下游边界位于海堤闸门处,以渤湾海区典型潮位过程为水位边界条件.出流条件采用1972年7月26日六米站典型潮位过程(见图4).根据有限体积计算方法,数学模型的过流通道主要有不泄流边界、自由出流边界、不透水坝、水位流量关系边界等,模型单元糙率范围为0.03~0.10.

图4 模型下游潮位边界Fig.4 Downstream tidal boundary of the model
2.4 数学模型验证
本次计算模拟的成果采用2008年《天津团泊洼蓄滞洪区建设与管理规划报告》中安全区规划前的洪水设计成果进行比较验证,分别为“56”型100年一遇洪水过程线设计结果及“63”型100年一遇洪水过程线设计结果,模型模拟结果的初步验证见表1.从表中可以看出,本次计算模拟的结果与设计结果基本一致,说明模型建立基本可行,计算结果基本可靠.

表1 模型模拟结果的初步验证Tab.1 Preliminary validation of model simulation results
模拟结果中的100年一遇主要通道流量过程和累积水量见图5和图6.
课程实验一般开学初制定好实验计划表,实验室是按计划进行相关实验的,平时不开放,按教学进度集中在某段时间实验,排得比较满,一个班接一个班。为了保证学生在有限的时间内顺利按时完成实验内容,实验过程中出现问题,由老师直接检查解决,实验老师人数多、老师能力强,实验做得就有保障。对于问题产生的原因和解决的方法,有学生问,老师才尽力讲解或先解决事后再解释,否则有可能影响后面的学生做实验,这样使得实验虽然做了,但达不到实验教学应有的效果。

图5 100年一遇洪水主要通道流量过程Fig.5 Flow progress of main channel at 1% flood frequency

图6 100年一遇洪水主要通道累积水量Fig.6 Accumulated outflow of main channel at 1% flood frequency
上游津浦铁路25孔桥来流过程是由天津南部洪水五洼联合调度确定的,马厂减河扒口洪水过程是洼淀间的内部衔接条件,沙井子行洪道入海口流量过程受海区潮位过程影响,呈现波动流量过程,从流量和水量变化趋势上看基本合理.
模拟结果中的100年一遇洪水淹没水位分布见图7.从图中水位变化趋势上看,津浦铁路25孔桥泄洪口下水位壅高,团泊洼内最高水位变化较平缓,马厂减河扒口上游形成快速下降水面,进入沙井子行洪道后最高水位变化且较平缓,受潮位顶托作用,入海口处最高水位与高潮位接近,水位分布基本符合洪水水面线变化规律.

图7 100年一遇洪水淹没水位分布Fig.7Inundation water level distribution at 1% flood freuency
以100年一遇洪水为例模拟模型流量过程0~690,h,分别选取30、90、150、210、300和690,h的区域淹没作为演示洪水的演进过程(如图8所示),从洪水演进过程上看,100年一遇洪水时在津浦铁路25孔桥开始宣泄洪水后的90多个小时后,到达马厂减河扒口,240,h左右洪水到达沙井子行洪道入海口.通过洪水演进模型定位、定量模拟滞洪过程的各物理量变化过程基本正确,可以用于模拟滞洪区洪水演进.

图8 100年一遇洪水演进过程Fig.8 Flood routing progress at 1% flood frequency
3 塔基建设前后洪水演进模拟
3.1 安全区基本情况简介
为了给团泊洼内经济社会提供可持续发展的防洪安全环境,拟对靠近滞洪区边缘的重要城镇及主要经济区建防洪圈围堤.防洪圈内不再承担滞洪任务,故将被保护区称为安全区.本次规划滞洪区内安排静海新城、团泊新城2个城镇级安全区,总面积为258.9,km2.同时为适应区域经济发展的需要,拟在天津市西青区团泊洼滞洪区和大港区沙井子行洪道建设电源线工程,线路由现状线路和新架线路组成,主要包括陈塘庄至迎丰站、静海至乾隆湖、腾飞路沿线3部分.
基于洪水宣泄路径和边界条件的需要,模型计算范围包括团泊洼滞洪区和大港区唐家洼至沙井子行洪道入海口.现以陈塘庄至迎丰站为例进行分析,评估所建电塔桩柱对滞洪区行洪的影响.
3.2 塔基建设前后洪水演进模拟对比
对塔基建设前后进行的洪水演进模拟方案包括:安全区规划前,塔基建设前后100年一遇洪水和200年一遇洪水;安全区规划后,塔基建设前后100年一遇洪水和200年一遇洪水.由于安全区的建设减小了滞洪面积,且200年一遇洪水流量过程较大,也更危险,因此,此处选择200年一遇洪水对安全区规划后塔基建设前后进行的洪水演进模拟进行说明.塔基建设前后其水深淹没分布见图9和图10,从图中可以看出,塔基建设前后无明显变化.
为了比较塔基建设工程前后对附近区域的影响,为局部加密模型水动力计算提供边界条件,将塔基所在的单元(单元位置、编号如图11所示)水位、流速变化分别列于表2和表3中.

图9 塔基建设前200年一遇洪水淹没水深分布Fig.9 Distribution of inundation water depth before pylon base construction at 0.5% flood frequency

图10 塔基建设后200年一遇洪水淹没水深分布Fig.10Distribution of inundation water depth after pylon base construction at 0.5% flood frequency

图11 塔基单元位置和编号Fig.11 Location and numbering of pylon base

表2 塔基所在单元的水位变化Tab.2 Variation of water level of the unit where the pylon base is located

表3 塔基所在单元的流速变化Tab.3 Variation of velocity of the unit where the pylon base is located
由表2中可以看出团泊洼安全规划后,200年一遇洪水电塔建设前电塔附近单元最大水深为5.562,m,发生在663号单元,位于团泊洼上部,在津浦铁路25孔桥扒口以东;最高水位为7.059,m,发生在663号单元,位置同上.电塔建设后电塔附近单元最大水深为5.584,m,最高水位为7.081,m,发生单元和位置无变化;水位最大壅高为0.022,m,发生在663号单元,位置同上.由表3中可以看出,团泊洼安全区规划后,200年一遇洪水电塔建设前电塔附近最大流速为1.701,m/s,发生在519号单元,位于静海新城安全区与团泊新城安全区之间,在线路路径的南端附近;电塔建设后电塔附近最大流速为1.693,m/s,发生单元和位置无变化;流速最大减小量为0.068,m/s,发生在579号单元,位于静海新城安全区与团泊新城安全区之间的中部,在团泊洼内线路路径的中部.
3.3 塔基基座局部加密模型构建
为了考察电塔基础桩柱对局部行洪的影响,对表2和表3中标有*处的单元中个体塔基局部进行加密计算.同时考虑塔基的不同形式,加密模型范围取30,m×30,m的正方形面积,模型底面为平面,在采用二维模型计算时,塔基模化为断面尺寸不变的淹没型圆柱、正方形柱体和露出水面型圆柱、正方形柱等不同情况.经过前期计算结果分析,塔基最不利工况为出水面4个塔基,每个塔基方柱边长1.2,m,间距5.28,m;极端不利工况为出水面4个塔基、塔基方柱外缘相接形成的不透水方柱,由于塔基上部塔身在行洪中可能拖挂杂物阻水,使塔基阻水高度增加,此次主要模拟最不利工况和极端不利工况,其布置见图12.

图12 塔基布置Fig.12 Distribution of the pylon bases
在整体模型中取工程前最大水深和最大流速为加密模型的水力条件,进行方案计算.塔基加密模型共有2个洪水频率对应的2种水深条件.工程建设后最不利工况为出水面4方柱,单塔基边长为1.2,m,单柱塔基中心间距为5.28,m的情况;极端不利情况为最不利工况条件下,出水面4方柱间完全被水中杂物堵塞,模化为单一大塔基的情况.加密模型计算共6个方案(见表4).

表4 加密模型计算方案Tab.4 Calculation schemes of refinement model
3.4 塔基基座局部加密模型计算结果
为反映工程后塔基附近的流场变化和水位壅高,对整个加密区工程前后流速变化差值和水位的壅高量等值线分布图进行比较,此处以方案3和方案4的结果为例,见图13和图14.从图中可以看出,流速变化和水位壅高分布基本合理.
为比较塔基建设前后的水深、流速在数值上的变化,在塔基附近取特征点1~8(见图12),同时考虑特征点位置有可能没有取在塔基附近水深、流速变化的极值处,加密模型区域中各方案工程建设前后最大水深、最大流速的比较见表5和表6.
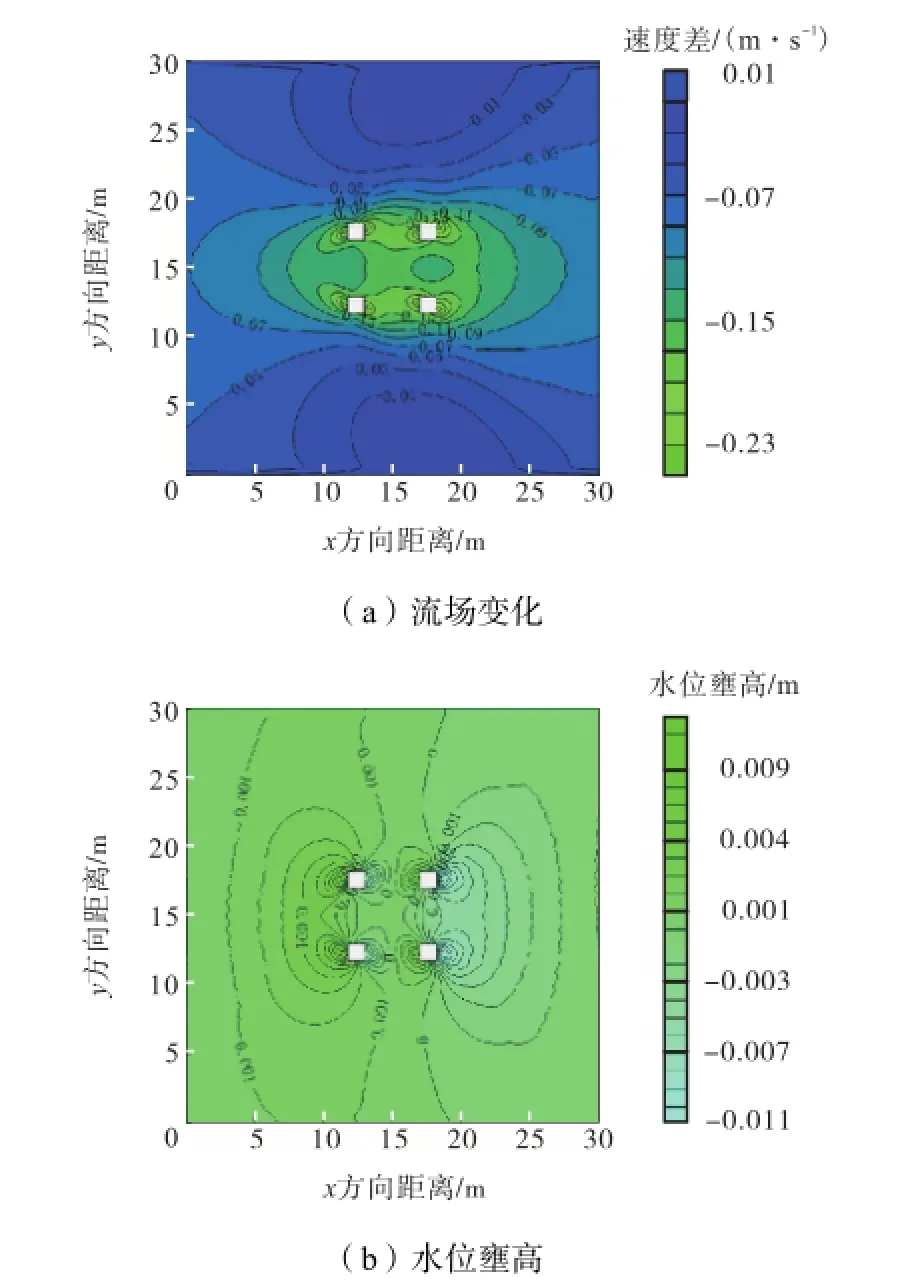
图13 方案3流场变化和水位壅高Fig.13 Variation of flow field and water level fluctuation of scheme 3
从表5中可以看出,100年一遇洪水现状(方案1)特征点上最大水深为5.223,m,出现在特征点1,在加密区拟建塔基的上游;最大流速为1.526,m/s,出现在特征点5,在加密区拟建塔基的下游.在塔基建设后的各方案中,特征点上最大水深为5.228,m,出现在特征点1,在方案5中塔基建设后的塔基上游;最大流速为1.459,m/s,出现在特征点3,在方案5中塔基建设后的下游塔基外侧面.

表5 模型特征点100年一遇洪水深和流速比较Tab.5Velocity comparison of flood water level at 1% flood frequency about character points of pylon base refinement model

图14 方案4流场变化和水位壅高Fig.14 Variation of flow field and water level fluctuation of scheme 4
从表6中可以看出,200年一遇洪水现状(方案2)特征点上最大水深为5.754,m,出现在特征点1,在加密区拟建塔基的上游;最大流速为1.726,m/s,出现在特征点4,在加密区拟建塔基的下游.在塔基建设后的各方案中,特征点上最大水深为5.760,m,出现在特征点1,在方案6中塔基建设后的塔基上游;最大流速为1.635,m/s,出现在特征点3,在方案6中塔基建设后的下游塔基内侧面.

表6 模型特征点200年一遇洪水深和流速比较Tab.6Velocity comparison of flood water level at 0.5% flood frequency about character points of pylon base refinement model
4 结 语
本文以洪水运动规律为基础,根据二维非恒定流方程,采用有限体积法对浅水环流方程进行了离散.同时通过“56”型洪水分洪流量过程,对水量、最大流量和淹没水位进行了验证,计算模拟的结果与设计结果基本一致,说明模型建立基本可行,计算结果基本可靠.
应用该模型对团泊洼安全区建设电塔塔基桩柱前后进行了100、200年一遇洪水演进的模拟,并通过构建电塔基座局部加密模型,分析了塔基建设前后对局部行洪、附近水深、流速的影响,为同等条件下滞洪区内工程建设提供了研究思路.
[1] 权 锦,张大伟,蒋云钟. 应用二维数值方法模拟蓄滞洪区洪水运动[J]. 水利水电技术,2012,43(4):107-111.
Quan Jin,Zhang Dawei,Jiang Yunzhong. Flood simulation flood storage and detention basin using 2-D numerical method[J]. Water Resources and Hydropower Engineering,2012,43(4):107-111(in Chinese).
[2] Cunge J A. On the subject of flood propagation computationmethod(Muskingum method)[J]. Journal of Hydraulic Engineering,1969,7:205-230.
[3] Akanbi A A,Katopodes N D. Model for flood propagationon initially dry land[J]. Journal of Hydraulic Engineering,1988,114(7):689-706.
[4] Caleffi V,Valiani A,Zanni A. Finite volume method forsimulating extreme flood events in natural channels[J]. Journal of Hydraulic Research,2003,41(2):167-177.
[5] 刘树坤,李小佩,李士功,等. 小清河分洪区洪水演进的数值模拟[J]. 水科学进展,1991,2(3):188-192.
Liu Shukun,Li Xiaopei,Li Shigong,et al. Numerical simulation of flood routing in the Xiaoqinghe Flood Plain[J]. Advances in Water Science,1991,2(3):188-192(in Chinese).
[6] 张艳霞,张小峰,杨芳丽. 长江与汉江两江洪水演进数学模型研究[J]. 中国农村水利水电,2008(6):32-34.
Zhang Yanxia,Zhang Xiaofeng,Yang Fangli. Integrated mathematical model research offlood routing for the Hanjiang River and the Yangtze River[J]. China Rural Water and Hydropower,2008(6):32-34(in Chinese).
[7] 谢作涛,张小峰,谈广鸣,等. 一维洪水演进数学模型研究及应用[J]. 武汉大学学报,2005,38(1):69-72.
Xie Zuotao,Zhang Xiaofeng,Tan Guangming,et al. Study and application of mathematical model for onedimensional flood-routing[J]. Engineering Journal of Wuhan University,2005,38(1):69-72(in Chinese).
[8] 王晓玲,李明超,周潮洪,等. 复杂河网中洪水演进二维数值仿真及其应用[J]. 天津大学学报,2005,38(5):416-421.
Wang Xiaoling,Li Mingchao,Zhou Chaohong,et al. 2D numerical simulation of flood routing in complex river network and its application[J]. Journal of Tianjin University,2005,38(5):416-421(in Chinese).
[9] 张细兵,欧治华,崔占峰,等. 基于非结构网格的分蓄洪区水沙演进数学模型研究[J]. 长江科学院院报,2011,28(4):75-79.
Zhang Xibing,Ou Zhihua,Cui Zhanfeng,et al. Unstructured grid model of flow and sediment evolutionin flood diversion and storage area [J]. Journal of Yangtze River Scientific Research Institute,2011,28(4):75-79(in Chinese).
[10] 王船海,李光炽. 行蓄洪区型流域洪水模拟[J]. 成都科技大学学报,1995,83(2):6-14.
Wang Chuanhai,Li Guangchi. Flood modeling for basin with regions of flood storage and relief[J]. Journal of Chengdu University of Science and Technology,1995,83(2):6-14(in Chinese).
[11] 周孝德,陈惠君,沈 晋. 滞洪区二维洪水演进及洪灾风险分析[J]. 西安理工大学学报,1996,12(3):244-250.
Zhou Xiaode,Chen Huijun,Shen Jin. Analysis of 2-D flood routing and flood damage risk in flood detention area[J]. Journal of Xi’an University of Technology,1996,12(3):244-250(in Chinese).
[12] 李大鸣,林 毅,徐亚男,等. 河道、滞洪区洪水演进数学模型[J]. 天津大学学报,2009,42(1):47-55.
Li Daming,Lin Yi,Xu Ya’nan,et al. Numerical model of flood propagation of rivers andflood detention basin[J]. Journal of Tianjin University,2009,42(1):47-55(in Chinese).
[13] 李大鸣,王 笑,赵明雨,等. 永定河泛区洪水调度数值模拟[J]. 天津大学学报:自然科学与工程技术版,2015,48(1):76-86.
Li Daming,Wang Xiao,Zhao Mingyu,et al. Flood dispatching numerical simulation for detention basins of Yongding River[J]. Journal of Tianjin University:Science and Technology,2015,48(1):76-86(in Chinese).
[14] Li Daming,Zhang Hongping,Li Bingfei,et al. Basic theory and mathematical modeling of urban rainstorm water logging[J]. Journal of Hydrodynamics:Ser B,2004,16(1):17-27.
(责任编辑:樊素英)
Research and Application of Flood Routing Mathematical Model for Tuanbowa-Shajingzi Flood Flowing Channel
Li Daming,Yang Zipei,Zhao Mingyu,Wang Xiao
(State Key Laboratory of Hydraulic Engineering Simulation and Safety,Tianjin University,Tianjin 300072,China)
A flood routing mathematical model was established using finite volume method based on basic twodimensional unsteady flow equations. With the real topography and geomorphology of Tuanbowa flood detention basin,the “56” type flood water diversion discharge process was simulated using the model and the results of water volume,the maximum flow and flood water level were basically consistent with design records. This model was applied to simulating the flood routing in Tuanbowa safety area before and after pylon base construction. Influences on local flood discharge,water depth and velocity near the tower base were analyzed by establishing pylon base refinement model,which may provide research basis for other engineering constructions of flood detention basin.
flood detention basin;Tuanbowa;flood routing;mathematical model
TV122
A
0493-2137(2015)08-0708-09
10.11784/tdxbz201311089
2013-11-28;
2014-05-16.
李大鸣(1957— ),男,博士,教授.
李大鸣,lidaming@tju.edu.cn.
