近红外脑功能DOT成像双网格半三维算法
2015-06-05周晓青贾梦宇赵会娟
刘 明,孟 伟,周晓青,贾梦宇,赵会娟,
近红外脑功能DOT成像双网格半三维算法
刘 明1,孟 伟1,周晓青1,贾梦宇1,赵会娟1,2
(1. 天津大学精密仪器与光电子工程学院,天津300072;2. 天津市生物医学检测技术与仪器重点实验室,天津300072)
采用基于光子输运模型的扩散层析成像(DOT)实现在近红外脑功能成像的诸多方案具有良好的定量研究潜力,但由于其逆问题固有的病态性,传统的全三维重建存在精度和分辨率低以及计算量大等缺点,因此根据实际问题约束和简化重建过程对改善成像性能具有重要意义.根据人体头部的解剖结构及近红外光在人脑中的传输特性,提出了改善逆问题病态性的双网格半三维图像重建算法,即在正问题中采用密集网格剖分下的全三维有限元计算提高计算精度,在逆问题中采用稀疏网格剖分且在同一脑组织层进行二维重建方法.模拟结果表明,对于单目标重建,双网格半三维重建算法与全三维重建算法相比,量化度提高30%、重建速度快4~12倍;对于双目标重建在信噪比30,dB以上的情况,半三维重建算法在CCS=12.5,mm的空间分辨能力与全三维重建算法CCS=20,mm的空间分辨能力相当.
脑功能成像;半三维算法;有限元;双网格
近红外(near infrared,NIR)脑功能成像是一种研究大脑血液动力学变化的非侵入式技术.该技术的优势体现在:①其具有无创、无辐射、高的时间分辨率、价廉可移动等特点,对于大脑的思维和意识等活动研究有着重要意义;②因其可在自然条件下进行监测,NIR脑功能成像具有很好的运动鲁棒性,该技术对新生儿和婴幼儿脑功能研究有着重要意义[1-2].此外,近红外光学成像技术还可用于诊断脑组织的某些生理异常,如血肿、脑室溢血、局部缺氧和缺血等.
目前商品化的近红外脑功能成像仪主要基于拓扑成像(optical topography,OT)原理[3-4].该成像方式假设探测区域下深度和横向方向的组织光学参数均匀分布,并利用修正的朗伯-比尔定律给出该区域组织的平均血氧浓度变化,因此OT可被认为是2D成像.虽然基于OT理论的NIR脑功能成像仪具有图像重建速度快的优点,但是具有3方面局限:①NIR脑功能成像仪是透过头皮、头骨来探测发生在灰质内的脑血液动力学变化,而OT假设源-探测点之间的组织光学参数为均匀分布,势必导致计算结果无法真实反映灰质内的血液动力学变化[5];②由于OT不具有深度分辨能力,因此,心跳、血压等正常生理活动将通过头皮的血液循环间接影响NIR脑功能仪的准确度[6];③由于修正的朗伯-比尔定律不能准确描述光在组织中传播的真实过程,因此限制了NIR脑功能仪的空间分辨率和量化度的进一步提高[7].
近年来,应用扩散层析成像(diffuse OT,DOT)理论进行脑功能成像的研究得到了越来越多的关注[8-10]. 在反射型DOT中,光在脑内传播是三维的,全三维重建可以得到任意深度内脑血氧的变化,但是由于成像区域大而导致图像重建速度过慢.同时,由于DOT重建中正问题和逆问题的计算中需要对成像空间进行离散,全三维重建将导致测量数据远远少于重建参数个数,因此逆问题的欠定性将十分严重.
对于实际的脑功能成像,人头可分为头皮、头骨、灰质和白质4部分.由于头皮层较薄且头骨对光的吸收大,因此可将头皮和头骨设为主要采用头骨的光学参数的均一的组织层.脑功能引起的脑血氧的变化主要发生在灰质中,由于探测系统信噪比的限制,源-探距离是有限的(一般为3,cm左右),此时NIR光只能到达的有限深度基本在灰质表层,因此可忽略灰质内光学参数沿深度的变化,同时将白质设为均一的组织层.综上所述,同时考虑到光子在非均匀组织中的三维传输,本文提出半三维图像重建算法,以弥补二维拓扑成像和三维图像重建的不足.
1 理论与方法
DOT系统可采用时域、频域、连续光(稳态)3种测量模式.由于连续光模式提供了简单的系统、快速的数据获取方式和较高的信噪比,因此在脑功能成像研究中被广泛地采用.本文对光在头内传输的正问题采用稳态扩散方程并利用有限元法进行求解[11].在图像重建中采用非线性最优化Newton-Raphson算法.在忽略脑功能活动引起的约化散射系数(sμ′)的变化时,逆问题求解简化为计算灰质内吸收系数(aμ)的微扰aμδ.采用迭代策略使吸收系数由相对粗略的初始估计逐步逼近真值[12-13],即

式中:χ为边界光子密度测量值;F(·)为正问题求解的边界光子密度值;Jμa为关于μa的Jacobian矩阵;上标i代表第i次迭代;δμi为第i次迭代的吸收系数
a微扰.
在全三维扩散层析成像图像重建中,要求重建组织体的某一个横断面甚至整个三维空间的光学参数图像,此时关于μa的Jacobian矩阵元素计算式为
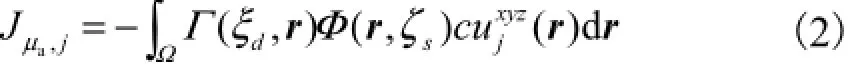
式中:j为有限元形函数体元编号;Ω为成像区域;Γ和Φ为光子能量密度;ξd为探测器所在位置,d=1,2,…,D;ζs为第s个光源所在位置,s=1,2,…,S;c为光在组织中的传播速度;r为区域内坐标矢量;uxyz(r)为有限元形函数.Γ(ξd,ζs)为边界光子能量密度,其中α是与边界条件有关的系数,在Robin条件下,fR为扩散传输内反射系数.
在本文提出的近红外扩散光半三维成像算法中,在正问题中,采用三维有限元法计算扩散方程,得到光子密度三维空间分布;在逆问题中,考虑在有限的源-探距离下漫反射光测量穿透深度的限制,重建过程采用半三维方式,在头部每一解剖结构层内均假设光学参数为二维分布,即该层沿深度方向光学参数相等,沿重建面方向光学参数为二维分布.由于NIR脑功能成像仪探测的是发生在灰质内的血氧变化,因此可进一步假设头皮、头骨和白质分别是均一物质,如图1所示.基于上述思想,近红外扩散半三维Jacobian矩阵元素计算方法可表示为
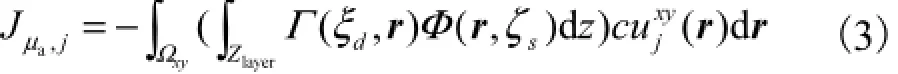
layer平面内新的有限元形函数.
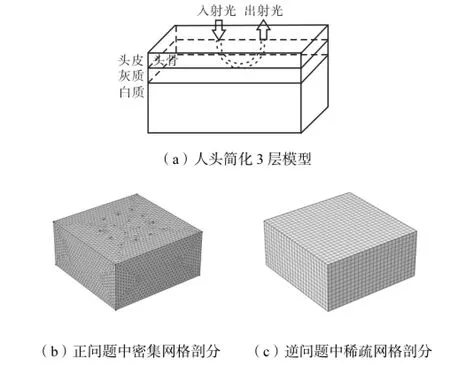
图1 人头简化3层模型与正、逆问题中的网格剖分Fig.1 Simplified view of three-lay head model,dense mesh for forward problem and sparse mesh for inverse problem
比较式(2)和式(3)可见,与全三维算法相比,采用半三维算法可减少逆问题重建节点数目,从而缩小了Jacobian矩阵规模,节约了计算时间.同时,由于重建节点数目变少,逆问题的病态性减弱,有望提高重建的量化度.
在近红外扩散光半三维重建算法中,对式(1)进行有限元离散化,计算过程中采用双网格剖分方式,如图1所示.在正问题中应用密集网格(见图1(b))的剖分计算节点光子能量密度,使漫射方程光子能量密度的解更精确.在光学参数重建过程中,根据半三维算法假设应用稀疏网格(见图1(c))进行计算,有利于减少重建中过多的自由度.
老龄化为养老保障带来巨大压力。随着人口平均预期寿命的上升,越来越多的人开始享受养老保障的福利,但上交老年保险的比例不是很高,导致保险行业盈利受阻,甚至负盈利[5]。人口老龄化会对医疗保险和老年保险形成冲击,不能有效解决这个问题将给我国经济社会带来负面影响。
采用稀疏网格分布,aμJ矩阵元素的上、下标分别表示源-探位置和各节点的坐标,则其Jacobian矩阵可以写为

式中X、Y、Z为3个坐标方向的坐标最大值.
考虑到半三维假设利用图1(a)中3层简化模型,则相应于式(4)同一层内的Jacobian矩阵元素可以表示为

同时,针对半三维重建,式(1)中的吸收系数微扰δμa可以用Ωxy平面内吸收系数微扰δμa代替.
2 模拟计算结果与分析
为验证本文所发展的双网格半三维算法(简称半三维算法)并与全三维算法进行对比,采用图2所示模型进行模拟验证.设模型体积为60,mm ×60,mm× 50,mm ,第1层厚度为5,mm,用来模拟头皮和头骨,背景光学吸收系数aμ设为0.01,mm-1,约化散射系数sμ′设为1,mm-1[14];第2层厚度为10,mm,用来模拟灰质背景,aμ设为0.02,mm-1,sμ′设为1,mm-1;第3层厚度为35,mm,用来模拟白质,其光学参数与灰质相同.设16个光源点和16个探测点以4×4方式均匀分布在顶平面上的中心,相邻最近两点之间相距10,mm,且探测点和源点重合.每个光源分别作用时,其余15个探测点同时接收对应位置的漫射光.重建过程应用Matlab和COMSOL Mutiphysics软件混合编程环境实现,重建目标为z=5,mm处灰质层横切面图像.在本文中,产生光子密度“测量值”和图像重建中的正问题所用的网格剖分相同.

图2 数值仿真所用的重建模型Fig.2Reconstruction models with one target and withtwo targets for numerical simulation
2.1 重建尺寸精度、量化度和速度分析
由于正问题的计算精度和网格剖分密度有关,为了获得合理的剖分密度,通过COMSOL Mutiphysics软件对图1(b)所示正问题模型采用不同剖分方式.在剖分过程中按照COMSOL Mutiphysics软件提供的“单元尺寸参数”为标准确定剖分网格疏密程度,分别产生采用极密集剖分时的35,010个节点以及采用密集剖分时的9,137个节点.采用图2(a)所示的单目标模型比较全三维算法和本文发展的双网格半三维算法的重建尺寸精度、量化度和速度.其中目标体为位于模型第2层中部的圆柱,半径为5,mm,吸收系数分别设为0.03、0.04、0.05,mm-1,用以模拟发生在灰质中的脑血氧变化.
计算微扰时正则化方法选用代数重建技术(ART),松弛因子取为0.1[15].在重建计算过程中通过迭代误差判断探测点上重建值,sdχ与“测量值”Fs,d(μa)的接近程度,误差定义为ε=0.03的迭代次数为迭代截止限制次数,其中newε为本次迭代误差,preε为前一次迭代误差.经多次模拟发现,在极密集网格剖分方式下,全三维算法迭代截止限制次数在20~30次之间.双网格半三维算法迭代截止限制次数在10~15次之间.
为了进一步比较所获得的图像,采用量化度(QR)、重建误差(QE)和半高宽(FWHM)对获得的结果进行评估.量化度定义为重建目标吸收系数和背景吸收系数之差与真实值之比[16];重建误差定义为重建吸收系数最大值与目标吸收系数最大值之差的绝对值与目标吸收系数之比;半高宽定义为某一方向上重建图像的形貌曲线的半高宽度.
图3(a)、(c)、(e)分别为密集网格剖分下对不同目标体采用全三维算法的重建图像,图3(b)、(d)、(f)分别为密集网格剖分下对不同目标体采用双网格半三维算法重建的图像,其中虚线为目标的真实大小及位置.图4为全三维和半三维算法对z=5,mm处重建的图像在y=30,mm时沿x方向重建值的形貌曲线,两种算法及真实目标分别用不同线型表示.图5和图6分别为极密集网格剖分下的形貌曲线及重建图像.

图3 采用密集网格下全三维算法与双网格半三维算法获得的重建图像Fig.3Reconstructed images by using 3D and dual mesh semi-3D algorithms under finer mesh for FEM calculation
对于不同吸收系数的目标体,采用密集网格与极密集网格剖分下全三维与半三维算法重建所得的结果如表1所示.从重建尺寸FWHM的角度,由于目标的真实直径为10,mm,半三维算法重建出的目标尺寸更接近真实值;从量化度QR角度,无论密集剖分还是极密集剖分,应用双网格半三维算法得到的量化度均高于全三维算法;从量化误差QE角度,在极密集网格下半三维算法的量化误差明显优于三维算法;从计算时间角度,在密集节点数下,采用半三维算法迭代1次的时间约为57,s,而采用全三维算法约需91,s;在极密集节点数下,采用半三维算法完成一次迭代的时间约为2,min,而采用全三维算法约需12,min.达到相同迭代截止限制条件,全三维算法的迭代次数约为双网格半三维算法的2倍.因此在极密集网格剖分下,双网格半三维算法将重建速度提高了约12倍.本模拟结果表明:对于大量有限元节点正问题的图像重建,半三维算法在量化度、计算时间和重建尺寸精度上明显优于全三维算法;对于半三维重建算法,采用极密集网格剖分比密集网格剖分获得更高质量的图像,因此在下文中均采用极密集网格剖分.
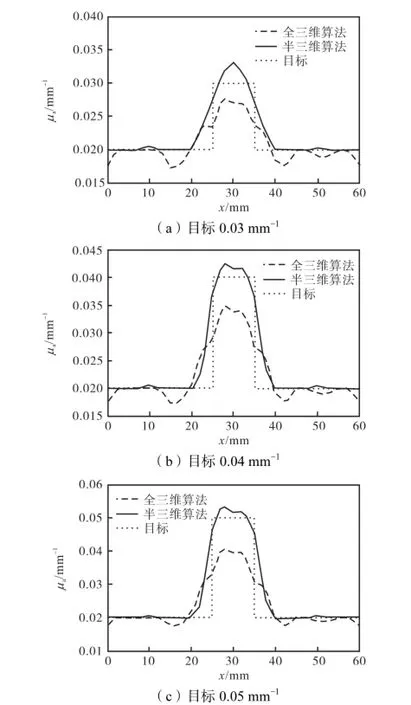
图4 采用密集网格下全三维算法与双网格半三维算法获得的形貌曲线Fig.4 Profile by using 3D and dual mesh semi-3D algorithms under finer mesh for FEM calculation
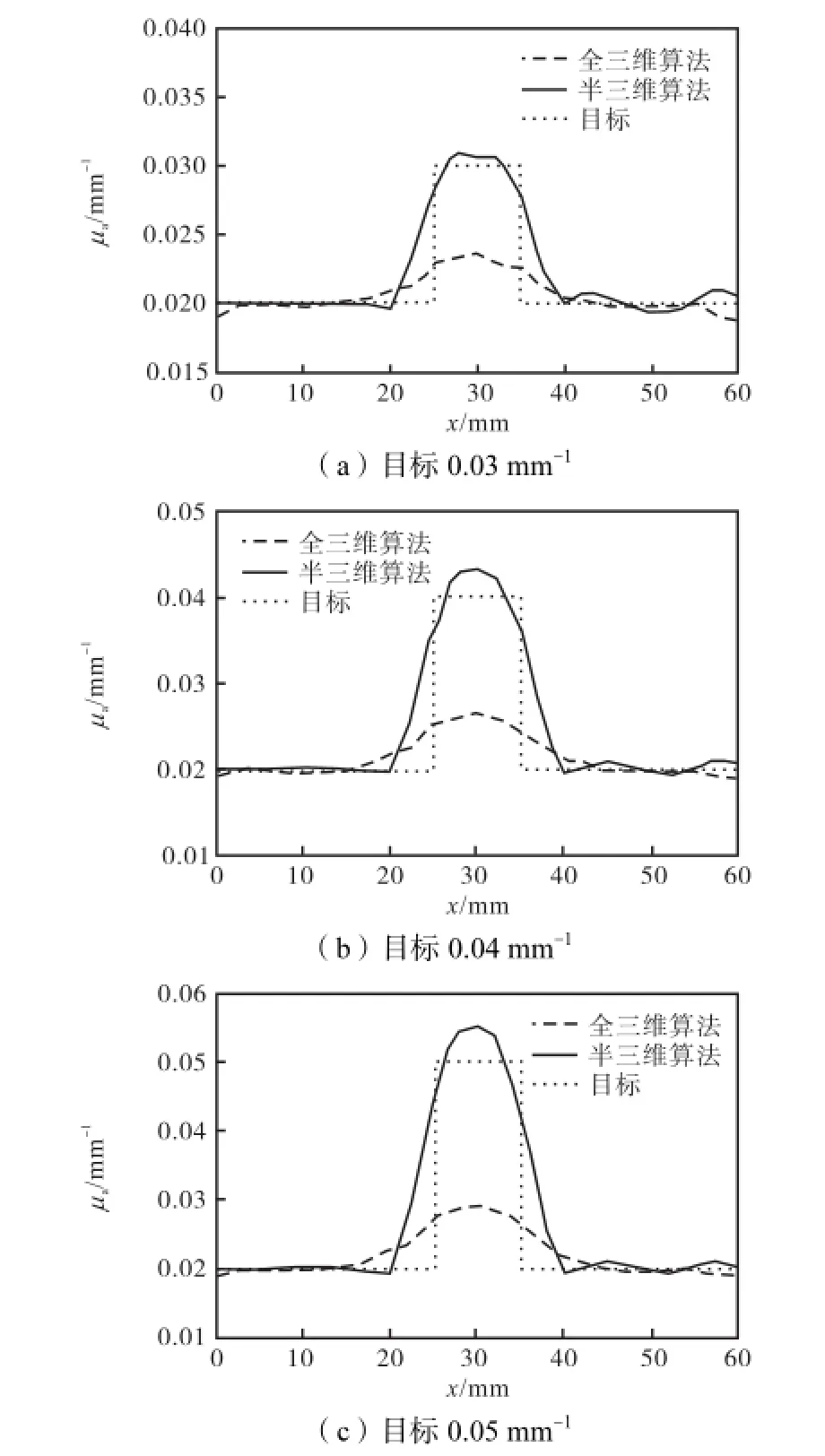
图5 采用极密集网格下全三维与双网格半三维算法获得形貌曲线Fig.5Profile by using 3D and dual mesh semi-3D algorithms under extra fine mesh for FEM calculation
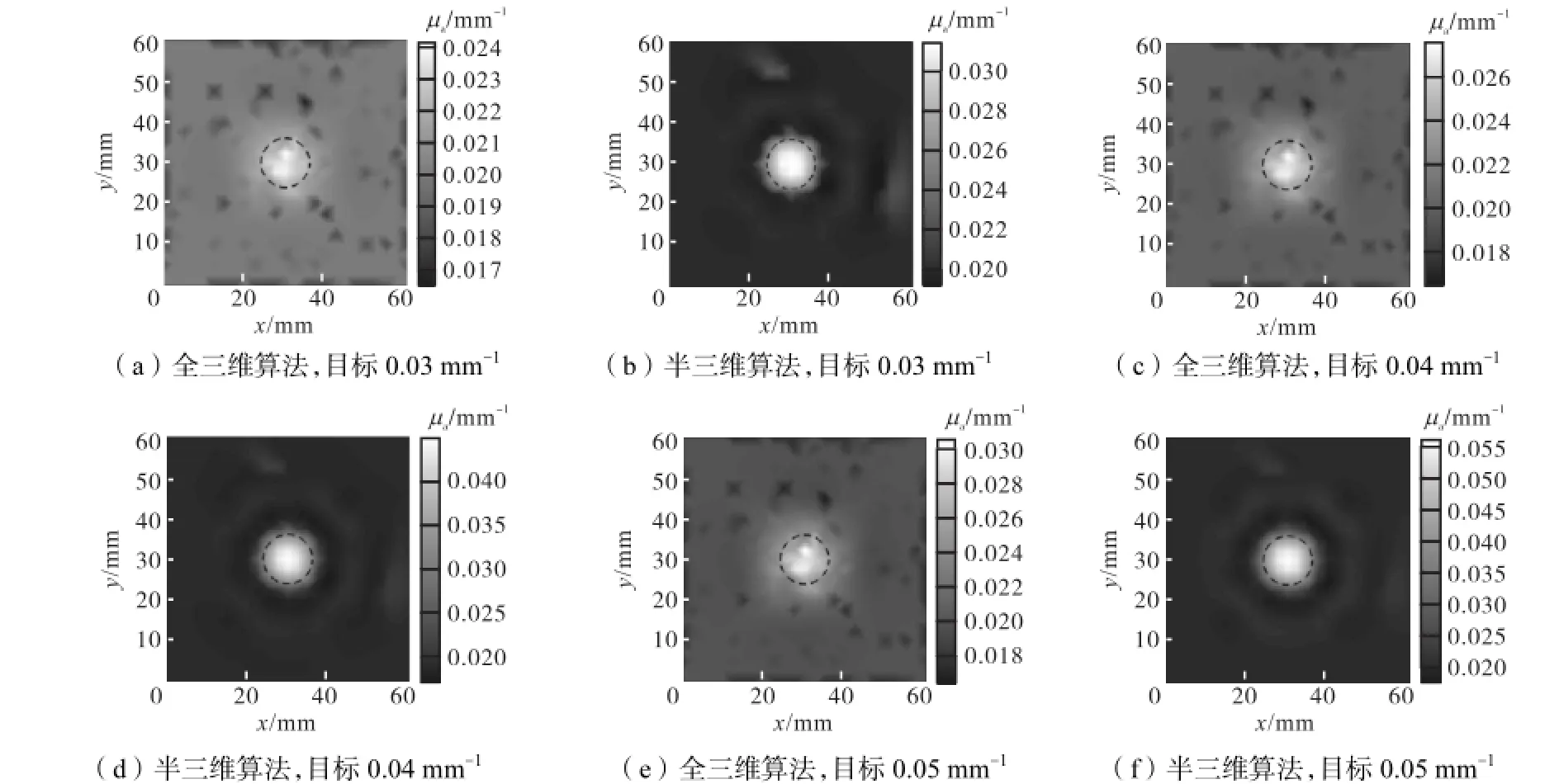
图6 采用极密集网格下全三维与双网格半三维算法获得的重建图像Fig.6 Reconstructed images by using 3D and dual mesh semi-3D algorithms under extra fine mesh for FEM calculation

表1 密集网格与极密集网格剖分下全三维与双网格半三维算法比较Tab.1 Comparison of 3D and dual mesh semi-3D reconstruction algorithms with finer mesh and extra fine mesh
2.2 空间分辨率与抗噪性分析
为进一步对比全三维算法和双网格半三维算法的空间分辨能力和抗噪性,采用图2(b)所示的双目标模型,两目标半径均为5,mm,吸收系数均为0.03,mm-1.
考虑到实际应用中光电倍增管等探测器会引起热噪声和散粒噪声等,向测量信号加入噪声形成新的“测量值”,如式(6)所示.
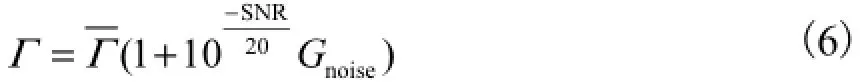
式中:Γ为无噪声的“测量值”;SNR为信噪比;Gnoise为高斯白噪声.
改变目标之间的中心距(CCS)使两目标不断靠近,令CCS分别为20.0、15.0、12.5,mm,即xy面上双目标最近点距离分别为10.0、5.0、2.5,mm,对模型进行图像重建,为了定量评估重建图像的空间分辨性,定义,即R=1时,两物体可被完全区分开,一般人眼可将两物体分开时的R>0.1.
图7和图8分别为固定信噪比SNR=40,dB下,CCS分别为20.0,mm和12.5,mm时全三维算法和双网格半三维算法获得的重建图像和形貌曲线.其中图8(a)、(b)分别为CCS=20.0,mm和12.5,mm时全三维和半三维算法对z=5,mm处重建的图像在y=30,mm时沿x方向重建值的形貌曲线,两种算法及真实目标分别用不同线型表示.
图9和图10分别为固定CCS=20.0,mm下,SNR分别为35,dB和30,dB时全三维算法和双网格半三维算法获得的重建图像和形貌曲线.其中图
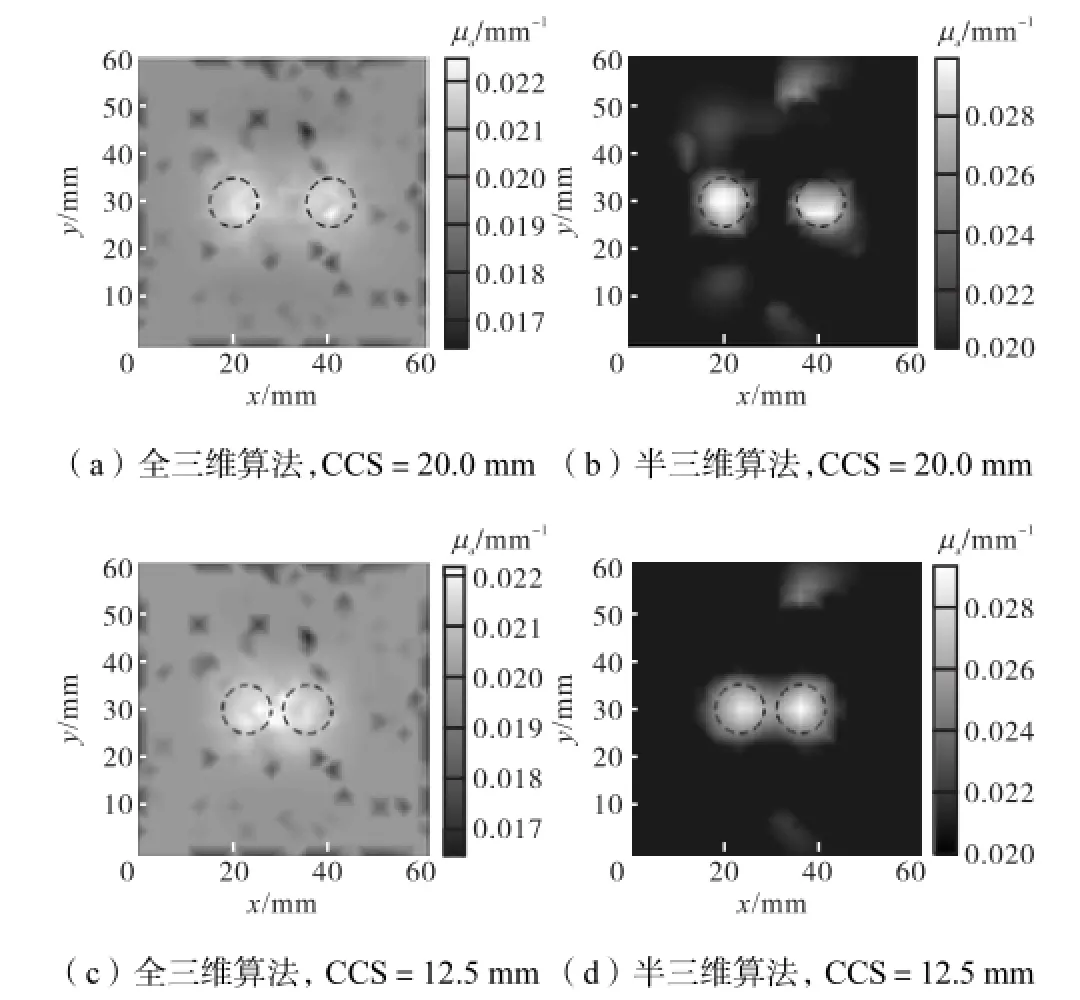
图7 信噪比SNR=40,dB,CCS分别为20.0,mm和12.5,mm时全三维和双网格半三维算法获得的重建图像Fig.7Reconstructed images when SNR is 40,dB and CCS is 20.0,12.5,mm respectively with 3D and dual mesh semi-3D algorithms
10(a)、(b)分别为SNR=35,dB和30,dB时全三维和半三维算法对z=5,mm处重建的图像在y=30,mm时沿x方向重建值的形貌曲线.在不同SNR和CCS下,采用全三维与半三维算法重建所得空间分辨率R如表2所示.双网格半三维算法的R值在相同CCS和不同SNR下都大于全三维算法的R值.在添加3个噪声的情况下,噪声增大,R降低,不易被分辨,并且影响重建目标形貌.在CCS为12.5,mm时,全三维算法的R已经小于0.1,即无法分辨双目标;而此时双网络半三维算法R≥0.3可对双目标进行分辨.重建过程的抗噪性与正则化方法有关,ART方法松弛因子的大小取决于测量信号的信噪比.如在松弛因子为0.1时,SNR小于30,dB则图像形貌较差.对比图10形貌曲线,双网格半三维算法在SNR=35,dB时的形貌优于SNR=30,dB;而全三维算法形貌曲线变化不明显.说明全三维算法在SNR为30,dB时抗噪性优于双网格半三维算法.结合算法的应用场合,在较高信噪比(SNR≥35,dB)的仪器系统,选用双网格半三维算法可获得更高的空间分辨率.
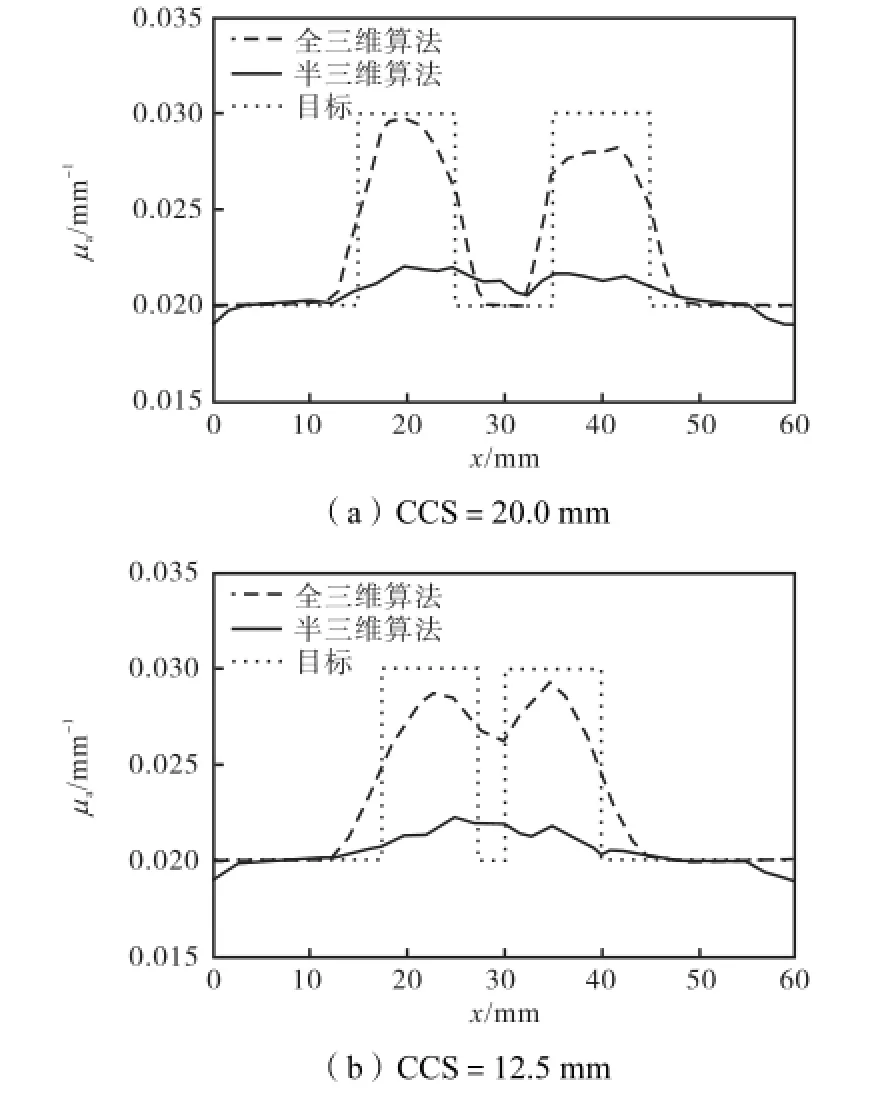
图8 信噪比SNR=40,dB,CCS分别为20.0,mm和12.5,mm时全三维和双网格半三维算法获得的形貌曲线Fig.8 Profile when SNR is 40,dB and CCS is 20.0,12.5,mm respectively with 3D and dual mesh semi-3D algorithms
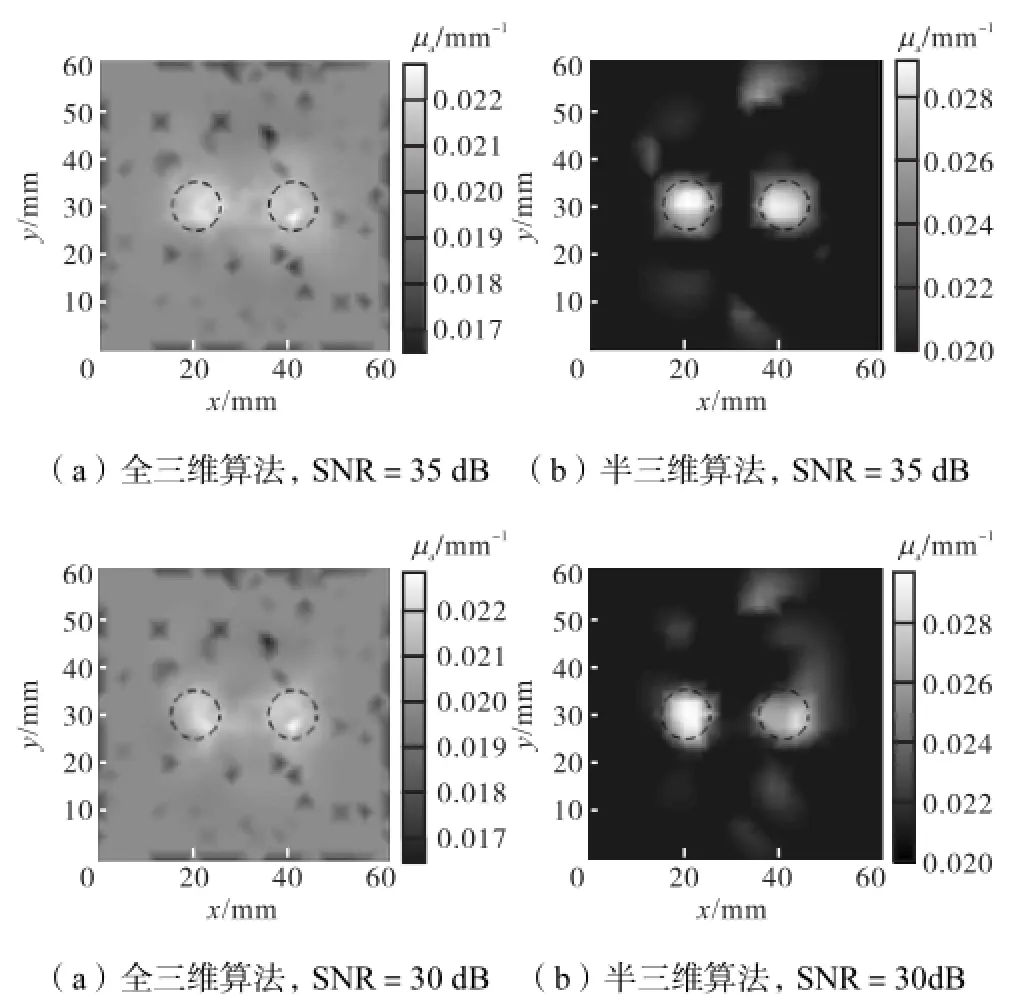
图9 信噪比SNR分别为35、30,dB,CCS为20.0,mm时全三维和双网格半三维算法获得的重建图像Fig.9 Reconstructed images when SNR is 35,30,dB respectively and CCS is 20.0,mm with 3D and dual mesh semi-3D algorithms
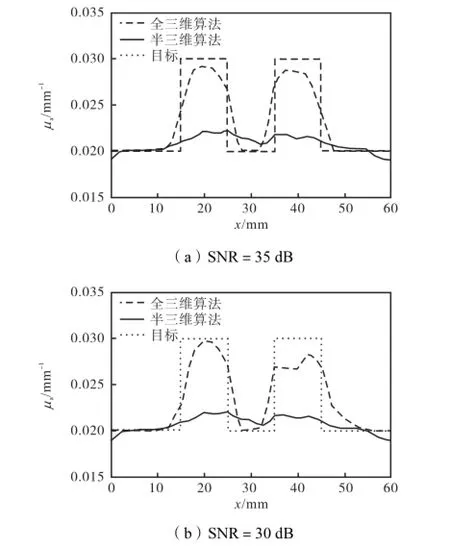
图10 信噪比SNR分别为35、30,dB,CCS为20.0,mm时全三维和双网格半三维算法获得的形貌曲线Fig.10Profile when SNR is 35,30,dB respectively and CCS is 20.0,mm with 3D and dual mesh semi-3D algorithms
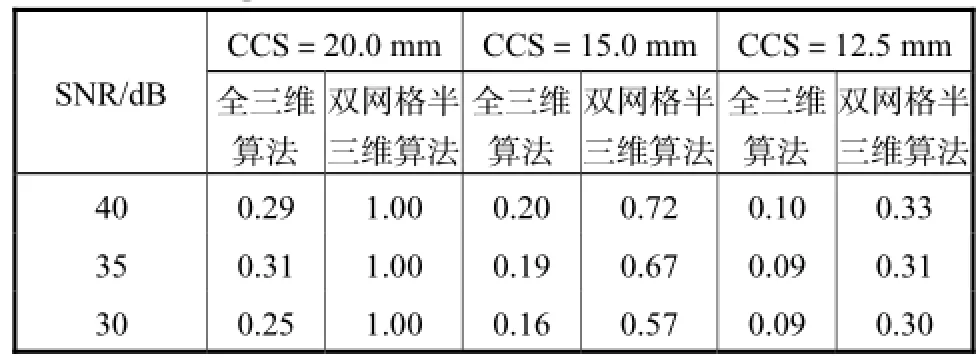
表2 全三维与双网格半三维算法空间分辨率RTab.2Comparison of R between 3D and dual mesh semi-3D algorithm
3 结 语
根据NIR脑功能成像特点,本文提出了近红外扩散光双网格半三维重建算法.模拟结果表明,本算法与全三维算法相比,由于对脑功能问题进行合理的假设,重建过程中采用双网格,在逆问题重建过程中有效地降低了重建节点数目,量化度明显优于全三维算法;同时节约了计算开销,提高了运算速度,对于网格节点数目越大的图像重建效果越明显,在正问题采用极密集网格剖分条件下本方法比全三维算法运算速度提高了约12倍.对双目标重建和添加噪声结果分析表明,半三维算法能够对双目标CCS≥12.5 mm、信噪比30,dB以上情况良好分辨.为了进一步验证本研究方法的实用性,实际脑组织功能成像实验将在后续进行研究.
[1] Hebden J C,Gibson A,Yusof R M,et al. Threedimensional optical tomography of the premature infant brain[J]. Physics in Medicine and Biology,2002,47:4155-4166.
[2] Koizumi H,Yamamoto T,Maki A,et al. Optical topography:Practical problems and new applications[J]. Applied Optics,2003,42(16):3054-3062.
[3] Huppert T J,Diamond S F,Franceschini M A,et al. HomER:A review of time-series analysis methods for near-infrared spectroscopy of the brain[J]. Applied Optics,2009,48(10):280-298.
[4] Hoshi Y,Huang J,Kohri S,et al. Recognition of human emotions from cerebral blood flow changes in the frontal region:A study with event related near-infrared spectroscopy[J]. Journal of Neuroimaging,2011,21(2):94-101.
[5] Yamada T,Umeyama S,Matsuda K,et al. Multidistance probe arrangement to eliminate artifacts in functional near-infrared spectroscopy[J]. Journal of Biomedical Optics,2009,14(6):064034.
[6] Näsi T,Mäki H,Hiltunen P,et al. Effect of taskrelated extracerebral circulation on diffuse optical tomography:Experimental data and simulations on the forehead[J]. Biomedical Optics Express,2013,4(3):412-426.
[7] Virtanen J,Noponen T,Meriläinen P,et al. Comparison of principal and independent component analysis in removing extracerebral interference from near-infrared spectroscopy signals[J]. Journal of Biomedical Optics,2009,14(5):054032.
[8] Franceschini M A,Joseph D K,Huppert T J,et al. Diffuse optical imaging of the whole head[J]. Journal of Biomedical Optics,2006,11(5):054007.
[9] Niu H,Guo P,Jiang T,et al. Improving image quality of diffuse optical tomography with a projection-errorbased adaptive regularization method[J]. Optics Express,2008,16(17):12423-12434.
[10] Perdue K L,Fang Q,Diamond S G.Quantitative assessment of diffuse optical tomography sensitivity to the cerebral cortex using a whole-head probe[J]. Physics in Medicine and Biology,2012,57(10):2857-2872.
[11] Arridge S R. Optical tomography in medical imaging[J]. Inverse Problems,1999,15(2):41-93.
[12] 秦转萍,赵会娟,杨彦双. 内窥式近红外频域漫射层析成像图像重构算法[J]. 天津大学学报,2012,45(5):423-429.
Qin Zhuanping,Zhao Huijuan,Yang Yanshuang. Image reconstruction method for endoscopic near-infrared frequency-domain diffuse optical tomography[J]. Journal of Tianjin University,2012,45(5):423-429(in Chinese).
[13] 金 蒙,高 峰,马文娟,等. 基于自然边界条件求解辐射传输方程的方法[J]. 天津大学学报,2011,44(9):816-822.
Jin Meng,Gao Feng,Ma Wenjuan,et al. A finite difference method to solve radiative transfer equation with natural boundary condition[J]. Journal of Tianjin University,2011,44(9):816-822(in Chinese).
[14] Tian Fenghua,Niu Haijing,Khan Bilal,et al. Enhanced functional brain imaging by using adaptive filtering and a depth compensation algorithm in diffuse optical tomography[J]. IEEE Transactions on Medical Imagine,2011,30(6):1239-1251.
[15] 马文娟,高 峰,张 伟,等. 基于辐射传输方程三阶简化球谐近似模型的时域荧光扩散层析图像重建方法[J]. 光学学报,2011,31(5):0510001.
Ma Wenjuan,Gao Feng,Zhang Wei,et al. Image reconstruction method of time-domain fluorescence diffuse optical tomography based on the third-order simplified spherical harmonics approximation to radiative transfer equation[J]. Acta Optica Sinica,2011,31(5):0510001(in Chinese).
[16] 周晓青,王 倩,范 颖,等. 面向大数据量的扩散光层析成像快速重建算法[J]. 光学学报,2013,33(4):0417001.
Zhou Xiaoqing,Wang Qian,Fan Ying,et al. Fast reconstruction scheme of diffuse optical tomography for dense sampling dataset[J]. Acta Optica Sinica,2013,33(4):0417001(in Chinese).
(责任编辑:赵艳静)
Dual Mesh Semi-3D Algorithm Towards NIR Diffuse Optical Tomographic Imaging of Brain Function
Liu Ming1,Meng Wei1,Zhou Xiaoqing1,Jia Mengyu1,Zhao Huijuan1,2
(1. School of Precision Instrument and Opto-Electronics Engineering,Tianjin University,Tianjin 300072,China;2. Tianjin Key Laboratory of Biomedical Detecting Techniques and Instruments,Tianjin 300072,China)
Diffuse optical tomography(DOT)based on the photon transport model provides good quantitative potential for near infrared cerebral functional imaging. Due to the inherent ill-posed inverse problem,the disadvantages of the traditional 3D reconstruction algorithm are low-precision,low-resolution and a big burden in calculation time. Therefore,the simplification and constraint of the reconstruction procedure according tothe practical situation have significant meaning. Based on the anatomic structure of head and the diffusive natureof near infrared light propagation in the brain,the semi-3D image reconstruction algorithm was proposed to alleviate the ill-posed problem. Namely,the dense mesh of 3D finite element method is used to improve the calculation accuracy in forward problem,and the sparse mesh of 2D image reconstruction algorithm is used in inverse problem by assuming that the optical properties in grey matter are invariable along the depth. Simulation results show that,for the single target sample,the quantitativeness ratio from the semi-3D reconstruction algorithm is 30%higher than that from the 3D reconstruction algorithm,and the reconstruction speed by using the semi-3D reconstruction algorithm is 4—12,times faster than that by using the 3D reconstruction algorithm. Additionally,for the two targets sample,the spatial resolution of the semi-3D reconstruction algorithm at CCS of 12.5,mm is almost the same as that ofthe 3D reconstruction algorithm at CCS of 20,mm with the value of SNR≥30.
cerebral functional imaging;semi-3D reconstruction algorithm;finite element method;dual mesh
TK448.21;Q63
A
0493-2137(2015)01-0062-08
10.11784/tdxbz201307070
2013-07-22;
2013-12-10.
国家自然科学基金资助项目(81101106,61108081,81271618);教育部高等学校博士学科点专项科研基金资助项目(20120032110056).
刘 明(1981— ),男,博士研究生.
赵会娟,huijuanzhao@tju.edu.cn.
时间:2014-01-07.
http://www.cnki.net/kcms/detail/12.1127.N.20140107.0915.002.html.
