基于非局部相似性和分类半耦合字典学习的超分辨率重建
2015-06-05杨爱萍钟腾飞何宇清
杨爱萍,钟腾飞,何宇清
基于非局部相似性和分类半耦合字典学习的超分辨率重建
杨爱萍,钟腾飞,何宇清
(天津大学电子信息工程学院,天津 300072)
为了提升单幅彩色图像的超分辨率重建质量,提出了一种改进的基于学习的超分辨率方法.针对半耦合字典学习超分辨率算法训练精度不高的缺陷,采用稀疏域分类与半耦合字典学习交替进行的启发式策略.在训练阶段引入稀疏域非局部相似性约束项,使用改进了的非局部约束l1范数优化问题求解算法,训练得到多组高、低分辨率字典和映射矩阵.在重建阶段利用分类稀疏表示、非局部相似性并结合残差补偿进一步提高重建精度.实验结果表明,该方法在主观和客观评价标准下均取得了较好的重建效果,显著提升了超分辨率重建质量.
超分辨率;半耦合字典学习;分类稀疏表示;非局部相似性
单幅图像超分辨率重建旨在利用一幅低分辨率图像获得高分辨率图像,以克服成像设备固有的分辨率限制.单幅图像超分辨率重建是数字图像处理领域的研究热点之一,在医学影像诊断、卫星遥感成像以及视频监控等领域均具有重要的应用价值[1-2].当前,单幅图像超分辨率重建算法主要分为基于插值的超分辨率算法、基于重建的超分辨率算法和基于学习的超分辨率算法3类.基于插值的超分辨率算法(如Bicubic插值[3])计算复杂度小、运行速度快,但易造成边缘锯齿和细节模糊.基于重建的超分辨率算法利用图像降质模型,结合特定的先验知识,对高分辨率图像进行重建,常用的先验知识有全变分(total variation,TV)先验[4]、平滑边界(soft edge)先验[5]和梯度轮廓(gradient profile)先验[6]等.人为假定的先验知识虽然能够提高超分辨率重建质量,但同样也是该类方法的局限性所在:对具有丰富的结构信息和柔和的纹理信息的自然图像而言,此类方法得到的超分辨率图像往往给人不够“自然”的视觉效果.
Yang等[7-8]从压缩感知理论出发,提出基于稀疏编码的超分辨率(sparse coding super-resolution,SCSR)算法,成为近年来国际上超分辨率领域的研究热点之一.该方法从高、低分辨率图像块集合中联合学习得到高、低分辨率冗余字典,使得训练集中的每个图像块都能在相应的字典下进行稀疏表示.在超分辨率重建过程中,首先计算低分辨率图像块在低分辨率字典下的稀疏表示系数,再由高分辨率字典与该稀疏表示系数相乘,得到高分辨率图像块的估计.该方法的字典学习过程中使用了Lee等[9]提出的拉格朗日对偶(Lagrange dual)算法和特征符号搜索算法(feature sign search algorithm),其通用性强的优点为算法的改进提供了较大的空间.Zeyde等[10]提出单幅图像超分辨率(single image super-resolution,SISR)算法,将测试图像自身作为训练样本学习字典,采用K-奇异值分解(K-singular value decomposition,K-SVD)算法[11]求低分辨率字典,再利用最优方向法(method of optimal direction,MOD)[12]求高分辨率字典,学习效率有所提升,得到了与Yang等[7-8]提出的SCSR方法相当的重建质量.基于SCSR和SISR算法,一些研究者从不同方面进行了改进.文献[13]引入图像块分类策略,将图像块分成平滑块、各方向边缘块和不规则块,并在每一类中训练字典.在重建阶段,把经过各类字典重建得到的高分辨率块根据重建误差进行加权,作为最终的高分辨率块的估计.文献[14]考虑到稀疏表示问题中训练信号空间的结构性,利用训练信号的非局部相似性特征,提出了基于非局部约束的稀疏表示算法.文献[15]采用了文献[14]中基于非局部约束的稀疏表示思想,将其应用于图像的超分辨率重建.文献[16]采用双层稀疏表示模型[17],直接以超分辨率重建误差作为优化问题的目标函数.
以上各方法虽然可小幅提升超分辨率重建质量,但都建立在“高、低分辨率图像块在相应字典下的稀疏表示系数相同”这一基本假设下,制约了重建质量的进一步提升.Wang等[18]提出半耦合字典学习(semi-coupled dictionary learning,SCDL)算法,对应的高、低分辨率图像块在相应字典下的稀疏表示系数不再假设是相同的,而是通过一个稀疏域的映射矩阵相联系.SCDL算法框架放宽了约束条件,增强了学习高、低分辨率图像块之间映射关系的能力,提高了重建质量,其在训练阶段可一并得到半耦合的高、低分辨率字典以及稀疏域映射矩阵,但由于采用了LARS算法[19]求解l1范数最优化问题,导致训练精度不高且限制了算法的改进.
本文针对半耦合字典学习算法的不足,提出了基于非局部相似性和分类半耦合字典学习的图像超分辨率重建算法.主要工作和创新点有:以半耦合字典学习算法为框架,引入基于映射误差的训练图像块稀疏域分类,并采用稀疏域分类与半耦合字典学习交替进行的启发式策略;在原有稀疏表示问题的l1范数约束项之外,引入稀疏域非局部相似约束项,在稀疏域挖掘训练图像块空间的结构化信息,以重建出更多高频细节;改进了文献[15]中基于非局部约束的稀疏表示算法,使其满足半耦合字典学习算法整体框架的要求;另外,在重建阶段引入了误差补偿机制,进一步提升超分辨率重建质量.
1 半耦合字典学习
图1为半耦合字典学习的基本思路,令X=[x1,x2,…,xn]和Y=[y1,y2,…,yn]表示高、低分辨率图像块数据矩阵,其中{xi,yi}是相应的高、低分辨率图像块对,Dx和Dy表示高、低分辨率字典,Sx和Sy表示高、低分辨率图像块数据矩阵在相应字典下的稀疏表示系数矩阵.不同于SCSR和SISR算法中的耦合字典学习,在半耦合字典学习框架下,高、低分辨率图像块的稀疏表示向量中,非零元素的位置和大小均不再假设是相等的,而是通过一个映射矩阵(见式(1))相联系.


图1 半耦合字典学习Fig.1 Semi-coupled dictionary learning
这种模型上的拓宽虽然客观上加大了字典和映射矩阵学习的复杂度,但本质上提升了模型的学习能力和稀疏表示精度,使得由观察图像lz得到的高分辨率图像的估计hˆy与真实高分辨率图像hy更相近.
在l1范数正则化的稀疏表示模型的基础上,添加映射误差惩罚项,并将高、低分辨率稀疏表示问题联立,得到半耦合字典学习模型[18],即

在Wang等[18]提出的SCDL算法中,式(2)可以转化为3个子问题交替求解,其中l1范数正则化的稀疏表示子问题使用了以LARS算法为基础的SPARS工具箱[20].该工具箱适合求解中小规模的稀疏表示问题,当训练数据规模较大时训练精度不高,且无法添加自定义的正则化项.
针对以上不足,本文提出了基于非局部相似性和分类半耦合字典学习的超分辨率重建算法,其整体上分为训练阶段和重建阶段,训练阶段离线进行,重建阶段利用离线学习得到的多类半耦合字典和稀疏域映射矩阵进行超分辨率重建测试.
2 训练阶段
2.1 交替启发式学习框架
图2为本文提出的训练阶段交替启发式学习框架.由于自然图像中存在着各种复杂的纹理块和边缘块,使用单一字典难以得到精确的稀疏表示,因而首先将训练图像块初始化分类.在每一类中进行半耦合字典学习,得到高、低分辨率字典和稀疏域映射矩阵;同时,利用图像块在稀疏域的非局部相似性,挖掘训练图像块空间的结构信息,以重建出更多高频细节.然后根据高、低分辨率稀疏表示系数在各类映射矩阵下的映射误差,将图像块进行重分类后,再次进行半耦合字典学习,如此循环,直到映射误差小于阈值算法终止.
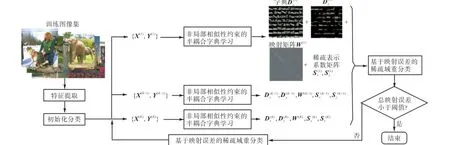
图2 交替启发式学习框架Fig.2 Alternant and heuristic learning framework
相对于具有特定分类规则的有人监督分类,交替启发式学习框架可以在学习过程中自适应地调整训练信号集的分类状况,在稀疏域映射误差最小目标下,使得各类训练信号更加集中,进而使得学习得到的各类字典更紧凑,稀疏表示精度更高.
2.2 训练数据获取与初始化分类
将训练图像集中的每一幅高分辨率图像{yrh}经模糊算子H、下采样算子P滤波并添加高斯噪声v后,得到相应的低分辨率图像{zrl},再经双三次插值算子A放大为原始尺寸的低分辨率图像{yr},用于特征提取.这一过程可表示为


在{yrh}上随机采样N个n×n的高分辨率图像块,向量化后构成矩阵形式X∈Rn×N;在{}的4幅滤波图像(滤波器为水平和垂直方向的一阶、二阶梯度算子)的相应位置采样得到低分辨率特征块,向量化后构成矩阵形式Y∈R4n×N.由于平滑块易造成稀疏分解不稳定,且平滑块通过双三次插值就能够较好重建,因此去除方差小于一定阈值的平滑图像块.而后将训练信号{X,Y}初始化分类为K类,记为,分类方法为K均值分类[21].为了方便表示,下文中除特别提及训练信号分类外,表示第i类的上标均省略.
2.3 稀疏域非局部相似性
稀疏表示的基本思路是用冗余字典中少数原子的加权组合近似表示输入信号[9].数据空间的分布并不均匀,例如自然图像中的小块具有一些特有的结构和模式,近期研究表明数据空间的结构化信息有助于提升稀疏表示的性能[14].由于稀疏分解的不稳定性,相似的数据其稀疏表示系数可能差别很大,导致重建误差较大,因此利用自然图像中的重复性结构,可有效提高稀疏表示的稳定性.
令ix和jx是两个数据向量,在字典D下的稀疏表示向量为is和js,若在原数据域jx是与ix第k最相似的数据向量,那么在稀疏域js也应当是与is第k最相似的稀疏表示向量.上述“稀疏域非局部相似性约束”,用ix的相似块稀疏表示系数的加权平均来估计is,即期望误差[14]

越小越好.其中,Ω是与ix前K个最相似的数据的下标集,jib为表示jx与ix相似程度的权重.

式中:h为可选择的参数;ci为归一化因子.令权重矩阵B的第j行第i列元素为bji,即B(j,i)=bji,则式(5)可写为
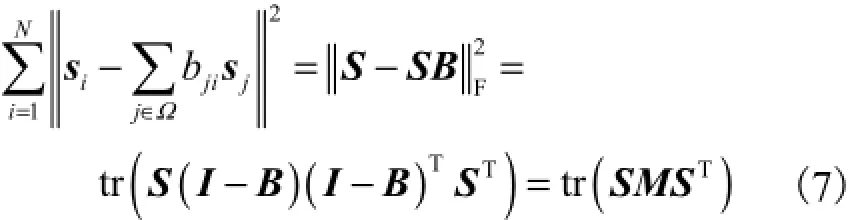
式中:tr()⋅是矩阵的迹运算;矩阵M由数据矩阵X经由权重矩阵B求得.
在原l1范数正则化的稀疏表示问题模型中引入稀疏域非局部相似性约束项[14],则数学模型为

式(8)可分解为关于字典D和稀疏表示系数S的两个子问题,分别利用Lagrange-Dual算法[9]和Feature-Sign改进算法[14]求解,两个子问题交替优化,直到式(8)收敛至局部最优解.
2.4 非局部相似性约束的半耦合字典学习
在式(2)半耦合字典学习中引入非局部相似性约束项,得到基于非局部相似性约束的半耦合字典学习模型,即

注意到式(9)关于3组优化变量{Dx,Dy}、{W}和{Sx,Sy}其中之一是凸优化问题,故采用文献[9]中的交替优化思路,将式(9)分解为3个子问题,即对应式(10)、(11)和(13),分别称之为“字典更新”、“映射矩阵更新”和“双任务稀疏分解”.
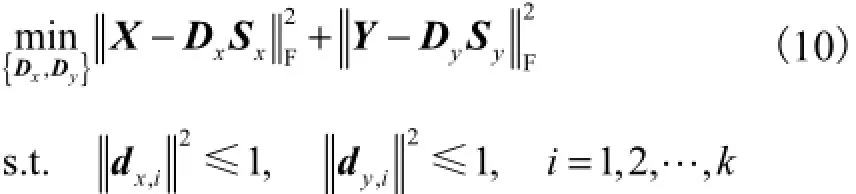
式(10)字典更新子问题的两个优化变量是可分离的,因此其可分解为2个二次约束的二次规划问题(QCQP),并利用Lagrange-Dual算法[9]分别求解.映射矩阵更新子问题可表示为
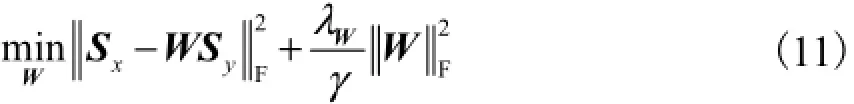
注意到式(11)实际上是岭回归问题,存在解析解
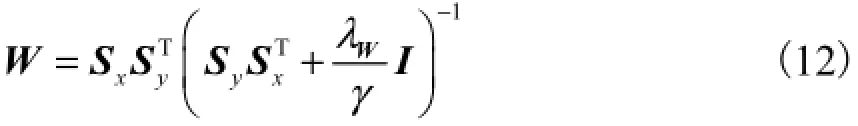
式中I为单位矩阵.
考虑到稀疏域映射矩阵W是线性的,可以采用双向学习策略,一并学习xS与yS之间的双向映射关系xy→W和yx→W,故双任务稀疏分解子问题的数学模型可表示为

为了利用Feature-Sign改进算法[14]求解式(13),将矩阵上下联立,并令

则式(13)可写成双任务的基于非局部相似性约束的稀疏表示问题,即

式(14)可利用Feature-Sign改进算法[14]交替优化2个子问题,直到收敛至局部最优解.
2.5 基于映射误差的稀疏域重分类
K均值分类的原理是在原信号域基于欧氏距离或其他度量,把信号归类到若干个自适应的分类中心向量周围.但在半耦合字典学习框架下,按照K均值分类(即初始化分类)得到的某一类信号,往往由于稀疏分解的不稳定性而得不到一个稳定的映射矩阵.因此,这里把在原信号域分类改为在稀疏域进行,将会大大降低总的映射误差使得各类中学习得到的稀疏域映射矩阵更稳定.基于映射误差的稀疏域重分类优化问题可表示为

式中c为训练信号的分类标号向量,其元素取值为1~k.基于映射误差的稀疏域重分类,实际上是将稀疏表示系数对{sx,i,sy,i}(对应原信号对{xi,yi})归类到使映射误差最小的映射矩阵W(i)对应的第i类中.
上述稀疏域重分类后,判断训练阶段的终止条件为:总映射误差是否小于一定阈值1δ.若是,则输出各类高、低分辨率字典各类稀疏域映射矩阵和各类稀疏表示系数矩阵;否则,继续在新分成的各类中进行第2.4节阐述的基于非局部相似性约束的半耦合字典学习,直至满足终止条件.
3 重建阶段
在超分辨率训练阶段,采用了稀疏域分类和半耦合字典学习交替进行的启发式学习策略.在重建阶段,也采用相同的交替启发式策略,利用非局部相似性和分类半耦合稀疏表示,并结合误差补偿机制重建图像,主要有4个步骤.
(1)输入低分辨率图像zl,初始化高分辨率图像yˆh0为zl的双三次插值;有重叠地在图像对应位置采样小块并提取特征,向量化后构成数据矩阵{XY},求解式(16)进行分类.
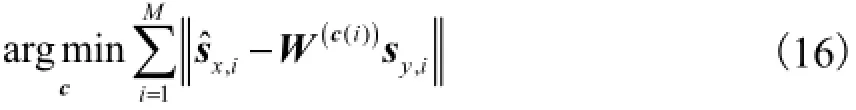
式中sˆx,i和sy,i分别为xˆi和yi在各类高、低分辨率字典下根据式(8)求出的稀疏表示向量.
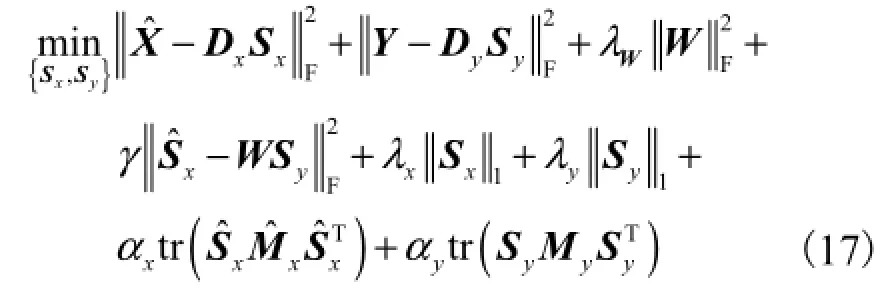

(4)误差补偿.将yˆh按照式(3)降质为低分辨率图像zˆl,计算残差图像e=zl-zˆl,并把残差图像e作为第(1)步的输入图像,重复步骤(1)~(3),得到残差图像e的超分辨率图像yˆh,e,进而得到最终的高分辨率图像,即

重建算法结束.
4 实验及结果分析
为了验证本文所提算法的有效性,在半耦合字典学习(SCDL)框架下,首先引入稀疏域非局部相似性约束(记为SCNL),再采用交替启发式学习与重建策略(记为SCNL_AH),最后引入误差补偿机制(记为SCNL_AHEC,即本文最终提出的算法),对Kodak Lossless True Color Image Suite图像集的24幅图像进行纵向对比实验,表1给出了引入各种策略后重建图像的PSNR值.
由表1可以看出,引入稀疏域非局部相似性约束,采用交替启发式学习与重建策略,以及引入误差补偿机制能够提升超分辨率重建质量.由于自然图像中含有大量重复性结构,引入稀疏域非局部相似性约束,起到了稳定稀疏分解的作用,显著提升了自然图像的超分辨率重建质量(见SCNL一列).求解稀疏表示与稀疏域重分类交替进行的交替启发式学习与重建策略,由于尽可能地降低了总映射误差,提高了映射矩阵学习的稳定性,因而较为明显地改善了重建质量(见SCNL_AH一列).误差补偿机制针对误差图像进行二次超分辨率,减小了可能存在的块效应和因稀疏表示引入的重建噪声,进一步增强了重建质量(见SCNL_AH_EC一列).
为将本文提出的新算法同现有的单幅图像超分辨率重建算法进行对比,选择近年来一些公认较优秀的超分辨率重建算法进行实验,包括Bicubic插值[3]、Yang等[8]的SCSR算法、Zeyde等[10]的SISR算法、Dong等[22]的自适应稀疏域选择-自适应正则化(adaptive sparse domain selection and adaptive regularization,ASDS-Reg)算法以及Dong等[23]的非局部集中稀疏表示(non-locally centralized sparse representation,NCSR)超分辨率算法.为了使对比更客观,将SCSR算法和SISR算法中所用的训练图像换成本文所使用的Berkeley Segmentation Data Set and Benchmarks 500(BSDS500)图像集;上述所有方法的测试图像均采用Kodak Lossless True Color Image Suite图像集.
实验中,统一条件和参数如下:下采样因子s=3;模糊算子为大小7×7、标准差σ=1.6的高斯模糊算子;图像块大小为5×5;相邻图像块有3个像素重叠;式(9)中各参数取值依次为:γ=0.5,λx=λy=0.1,λW=0.01,αx=αy=0.2.以图像Kodim_23为例,各算法的超分辨率重建结果及其局部放大图如图3所示.

图3 各算法超分辨率重建结果Fig.3 Comparison of several super-resolution methods
由图3可看出,与Bicubic插值相比,Yang等的SCSR算法和Zeyde等的SISR算法,重建图像具有更强的边缘锐利度,但在局部区域,如眼睛左上方的纹理处,存在明显的伪边缘和噪声.Dong等的ASDS-Reg算法重建图像虽然显著减少了伪边缘和噪声,但丢失了过多的纹理细节,如眼睛下方的纹理边缘过于平滑.NCSR算法与ASDS-Reg相比,重建出了更多的细节,但某些纹理依然存在锯齿效应.本文算法在重建纹理细节和消除伪边缘与锯齿两方面,同时做到了较好的效果,其主观视觉效果在以上几种方法中达到最优.
为了客观评价上述超分辨率重建算法,对柯达无损彩色图像集的24张图像分别应用各算法进行超分辨率重建,表2给出了上述各超分辨率算法重建图像的PSNR值.由表2可看出,本文提出的基于非局部相似性和半耦合字典学习的超分辨率重建算法,在大多数测试图像上均取得了较高的PSNR值,仅在其中2张图像上略逊于NCSR算法.

表2 各超分辨率算法重建图像的PSNR值Tab.2 PSNR of reconstructed images with several super-resolution algorithms dB
5 结 语
针对单幅彩色自然图像的超分辨率重建问题,笔者在半耦合字典学习算法框架的基础上,引入了稀疏域非局部相似性约束项,挖掘训练图像块空间的结构化信息,重建出了更多的图像高频细节;同时根据映射误差大小在稀疏域进行重分类,采用“学习-重分类-学习”交替进行的启发式策略,训练得到多组字典和稀疏域映射矩阵.另外,在重建阶段引入误差补偿机制,对残差图像进行二次超分辨率处理.实验结果表明,本文提出的基于非局部相似性和分类半耦合字典学习的超分辨率重建算法能够大大提高超分辨率重建质量.
[1] Baker S,Kanade T. Limits on super-resolution and how to break them[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence,2002,24(9):1167-1183.
[2] Park S C,Park M K,Kang M G. Super-resolution image reconstruction:A technical overview [J]. IEEE Signal Processing Magazine,2003,20(3):21-36.
[3] Keys R. Cubic convolution interpolation for digital image processing [J]. IEEE Transactions on Acoustics,Speech and Signal Processing,1981,29(6):1153-1160.
[4] Marquina A,Osher S J. Image super-resolution by TV-regularization and Bregman iteration [J]. Journal of Scientific Computing,2008,37(3):367-382.
[5] Dai S,Han M,Xu W,et al. Soft edge smoothness prior for alpha channel super resolution[C]// Proceedings of IEEE Computer Society Conference on Computer Vision and Pattern Recognition. Minneapolis,USA,2007.
[6] Sun J,Xu Z,Shum H-Y. Image super-resolution using gradient profile prior[C]// Proceedings of IEEE Computer Society Conference on Computer Vision and Pattern Recognition. Anchorage,USA,2008.
[7] Yang J,Wright J,Huang T,et al. Image superresolution as sparse representation of raw image patches[C]// Proceedings of IEEE Computer Society Conference on Computer Vision and Pattern Recognition. Anchorage,USA,2008.
[8] Yang J,Wright J,Huang T,et al. Image superresolution via sparse representation [J]. IEEE Transactions on Image Processing,2010,19(11):2861-2873.
[9] Lee H,Battle A,Raina R,et al. Efficient sparse coding algorithms[C]// Proceedings of Advances in Neural Information Processing Systems. Vancouver,Canada,2006:801-808.
[10] Zeyde R,Elad M,Protter M. On single image scale-up using sparse-representations[C]// Proceedings of Curves and Surfaces. Avignon,France,2012:711-730.
[11] Aharon M,Elad M,Bruckstein A. K-SVD:An algorithm for designing of overcomplete dictionaries for sparse representations [J]. IEEE Transactions on Signal Processing,2006,54(11):4311-4322.
[12] Engan K,Aase S O,Hakon Husoy J. Method of optimal directions for frame design[C]// Proceedings of IEEE International Conference on Acoustics,Speech and Signal Processing. Phoenix,USA,1999:2443-2446.
[13] Yang S,Wang M,Chen Y,et al. Single-image superresolution reconstruction via learned geometric dictionaries and clustered sparse coding [J]. IEEE Transactions on Image Processing,2012,21(9):4016-4028.
[14] Zheng M,Bu J,Chen C,et al. Graph regularized sparse coding for image representation [J]. IEEE Transactions on Image Processing,2011,20(5):1327-1336.
[15] Lu X,Yuan H,Yan P,et al. Geometry constrained sparse coding for single image super-resolution [C]// Proceedings of IEEE Computer Society Conference on Computer Vision and Pattern Recognition. Providence,USA,2012:1648-1655.
[16] Yang J,Wang Z,Lin Z,et al. Coupled dictionary training for image super-resolution [J]. IEEE Transactions on Image Processing,2012,21(8):3467-3478.
[17] Yang J,Wang Z,Lin Z,et al. Bilevel sparse coding for coupled feature spaces[C]// Proceedings of IEEE Computer Society Conference on Computer Vision and Pattern Recognition. Providence,USA,2012:2360-2367.
[18] Wang S,Zhang D,Liang Y,et al. Semi-coupled dictionary learning with applications to image superresolution and photo-sketch synthesis[C]// Proceedings of IEEE Computer Society Conference on Computer Vision and Pattern Recognition. Providence,USA,2012:2216-2223.
[19] Efron B,Hastie T,Johnstone I,et al. Least angle regression[J]. The Annals of Statistics,2004,32(2):407-499.
[20] Mairal J,Bach F,Ponce J,et al. Online dictionary learning for sparse coding [C]// Proceedings of the 26th Annual International Conference on Machine Learning,ACM. New York,USA,2009:689-696.
[21] Kanungo T,Mount D M,Netanyahu N S,et al. An efficient k-means clustering algorithm:Analysis and implementation [J]. IEEE Transactions on Pattern Analysis and Machine Intelligence,2002,24(7):881-892.
[22] Dong W,Zhang L,Shi G,et al. Image deblurring and super-resolution by adaptive sparse domain selection and adaptive regularization [J]. IEEE Transactions on Image Processing,2011,20(7):1838-1857.
[23] Dong W,Zhang L,Shi G,et al. Nonlocally centralized sparse representation for image restoration [J]. IEEE Transactions on Image Processing,2013,22(4):1620-1630.
(责任编辑:赵艳静)
Super-Resolution Reconstruction Based on Non-Local Similarity and Clustered Semi-Coupled Dictionary Learning
Yang Aiping,Zhong Tengfei,He Yuqing
(School of Electronic Information Engineering,Tianjin University,Tianjin 300072,China)
In order to improve the super-resolution reconstruction quality of single color image,a modified learning based super-resolution approach was proposed. To resolve the problem of low training accuracy of semi-coupled dictionary learning(SCDL)super-resolution algorithm,this paper presented a novel heuristic strategy in which clustering in sparse domain and semi-coupled dictionary learning were performed in turn. In training phase,the non-local similarity constrain term in sparse domain was introduced into the optimization function,and then several groups of highlow resolution dictionaries and mapping functions were trained by a modified non-locally constrained l1-norm optimization algorithm. In reconstruction phase,combined with residual compensation,clustered sparse representation and non-local similarity were used to further improve the super-resolution reconstruction quality. Experimental results show that the proposed approach can achieve better reconstruction effect in both subjective and objective evaluation criteria and significantly improve the quality of super-resolution.
super-resolution;semi-coupled dictionary learning;clustered sparse representation;non-local similarity
TN911.73
A
0493-2137(2015)01-0087-08
10.11784/tdxbz201309026
2013-09-06;
2013-11-11.
国家自然科学基金资助项目(61002027,61372145).
杨爱萍(1977— ),女,博士,副教授.
杨爱萍,yangaiping@tju.edu.cn.
时间:2014-01-06.
http://www.cnki.net/kcms/detail/12.1127.N.20140106.1455.001.html.
