基于改进型LuGre模型的自适应滑模摩擦补偿方法
2015-06-05谭文斌李醒飞裘祖荣向红标张晨阳
谭文斌,李醒飞,裘祖荣,向红标,张晨阳
基于改进型LuGre模型的自适应滑模摩擦补偿方法
谭文斌1,2,李醒飞1,裘祖荣1,向红标3,张晨阳2
(1. 天津大学精密测试技术及仪器国家重点实验室,天津 300072;
2. 天津商业大学机械工程学院,天津 300131;3.天津理工大学机械工程学院,天津 300384)
为建立具有良好动态性能的开放式伺服系统,针对自适应摩擦补偿对未知建模误差和扰动抑制能力较弱的问题,提出了一种基于修正黏性摩擦LuGre模型的自适应滑模摩擦补偿方法.建立开放式伺服系统的动力学方程,并结合修正黏性摩擦LuGre模型,提出伺服系统的状态方程.根据反演设计的思想,设计自适应滑模摩擦控制器以及相应的自适应律和切换函数,并分析了其全局渐进稳定性.通过可编程多轴控制器(PMAC)实现了该补偿控制方案在开放式伺服平台的应用,并通过实验验证了其有效性.实验结果表明:与自适应摩擦补偿相比,该自适应滑模摩擦补偿方案在输入信号为正弦信号时,伺服系统的跟踪误差由±6.9,µm降低到±4.1,µm.采用该补偿方案可有效地抑制摩擦及其他不确定干扰对伺服系统的不利影响,进一步提高伺服系统的跟踪性能.
LuGre模型;自适应滑模控制;摩擦补偿
摩擦补偿是构建高精度伺服系统的重要环节,已成为目前伺服控制策略的研究热点之一[1].摩擦补偿策略一般可以分为两类:基于摩擦模型的补偿策略以及不依赖于摩擦模型的补偿策略.其中,基于摩擦模型的补偿策略是一种从本质上补偿伺服系统摩擦的方法,但是只有其采用的摩擦模型及模型参数都十分精准的情况下,才能实现精确的摩擦补偿.而随着伺服系统工作时间的增加,传动机构将不可避免地产生磨损,同时润滑情况也会出现一些改变,从而导致补偿所依赖的摩擦模型的参数不可避免地产生变化,此时必须重新进行复杂的参数辨识,才能保证补偿的精度[2-3].
自适应摩擦补偿基于摩擦模型,并进行模型参数的在线估计,能够在摩擦参数发生一定变化的情况下实现较好的补偿效果.Gilbart等[4]最先提出将自适应控制应用于摩擦补偿,采用了模型参考的自适应控制结构.王发智等[5]针对光电平台提出一种基于Stribeck静态摩擦模型的自适应摩擦补偿方法.Minh等[6]采用双观测器估计LuGre模型中的不可测状态,并设计了基于李雅普诺夫稳定性原理的自适应补偿控制器.向红标等[3]则基于LuGre模型,对开放式伺服平台进行了自适应摩擦补偿.但是自适应控制不能很好地解决伺服系统中存在的不确定非线性项,鲁棒性较差,而且需要摩擦模型具有较高的精确性.而在实际伺服系统中,建模误差和外部扰动不可避免地存在,从而限制了自适应控制的效果,降低了伺服系统的低速跟踪性能,甚至可能造成系统不稳定[7].
滑模控制是一种非线性的控制方法,利用其滑动模态,通过切换状况的改变来克服不确定性,不仅可以满足系统内部参数变化的需要,同时对各种不确定性扰动也具有很好的适应性.Sankaranarayanan等[8]对各种摩擦模型进行分析,得到了各模型的共性,并以此进行伺服系统滑模变结构控制.Young[9]根据滑模变结构的模态切换特性和摩擦在零速时的不连续现象,也采用滑模变结构对伺服系统进行摩擦补偿.但是,滑模控制也存在一定的缺陷,如系统产生抖振现象.
自适应滑模控制是自适应控制和滑模控制的有机结合,既可解决系统参数不确定及参数时变问题[10],又能抑制滑模控制的抖振现象,因此可以更精确地实现摩擦补偿.
本文针对高精度开放式伺服平台中摩擦模型的参数变化以及伺服系统中不确定的非线性建模误差与扰动,提出了一种基于改进型LuGre模型的自适应滑模摩擦补偿方法.利用反演设计方法,通过递推Lyapunov函数设计了自适应滑模控制器,并分析了其稳定性和渐进收敛性.
1 系统构成
如图1所示,高精度开放式伺服平台由工业控制计算机、可编程多轴控制器(programmable multi-axis controller,PMAC)、伺服驱动器、伺服电机、滚珠丝杠螺母副、直线导轨和移动平台组成.
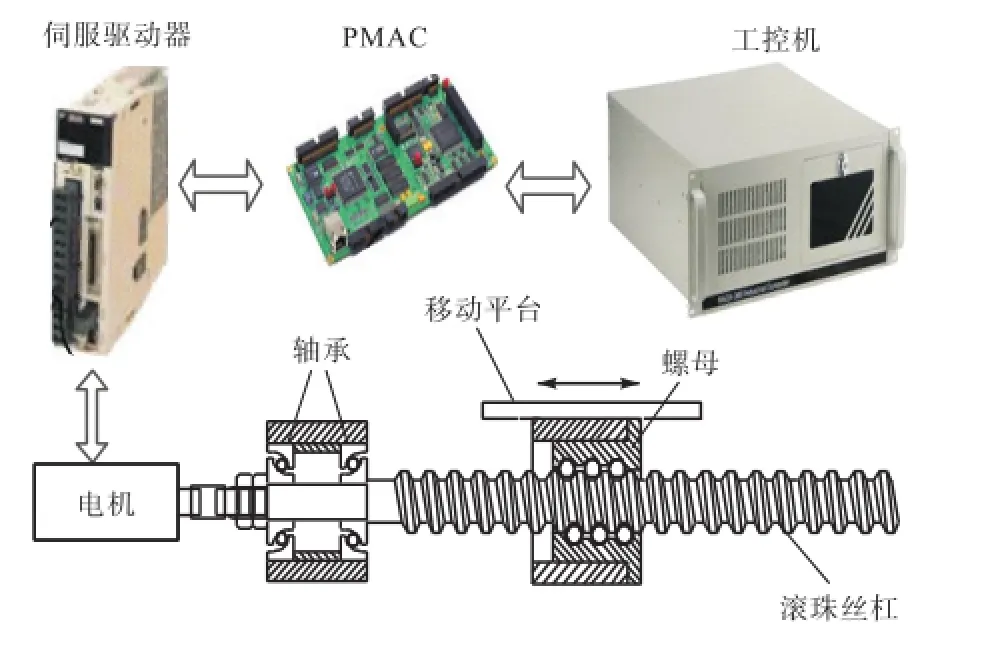
图1 系统结构Fig.1 System structure diagram
2 系统动力学方程
图2所示为伺服系统的简化模型,其中,r、x分别为期望位移和实际位移,u为运动控制卡PMAC的输出,θ为电机转角,θ˙为电机角速度,fT为伺服系统的等效摩擦,JL为转动惯量,Km为PMAC数字输出到驱动器转矩输出的转换系数,Kcts为转角与移动平台直线位移的转换系数,s为传递函数中的一个变量.
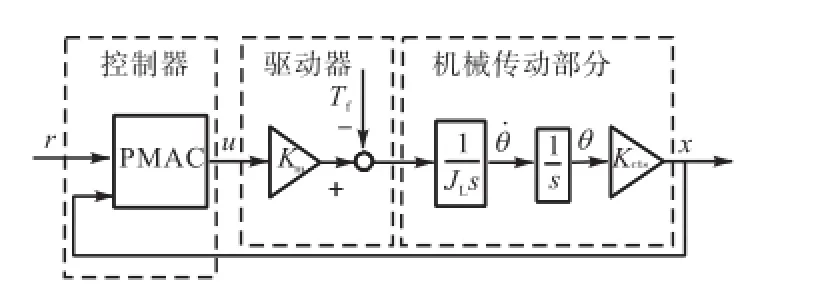
图2 伺服系统简化模型Fig.2 Simplified model of servo system
根据图2可得到伺服系统动力学方程为

式中x˙˙为位移加速度.fT可由修正黏性摩擦的LuGre模型[11]描述为
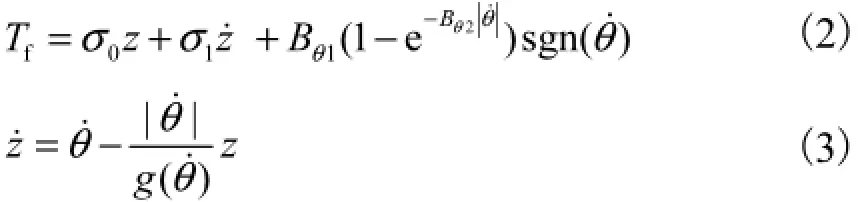
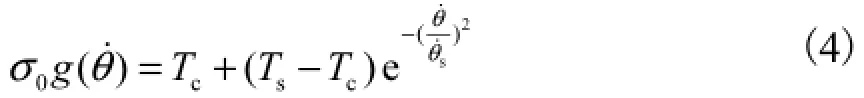
式中:σ0为刚性系数;σ1为阻尼系数;Tc为库伦摩擦力矩;Ts为静摩擦力矩;1Bθ为黏性摩擦斜率因子;Bθ2为黏性摩擦变化因子;θ˙s为切换速度;z为接触面的鬃毛平均变形;g(θ˙)严格正实且有界.
3 自适应滑模控制器设计
考虑摩擦参数的变化,将原摩擦模型进行修改:与z有关的部分通过α反映其变化;黏性摩擦部分通过β反映其变化;此外增加项Δ反映条件变化时的建模误差以及其他不确定扰动.修改后Tf描述为
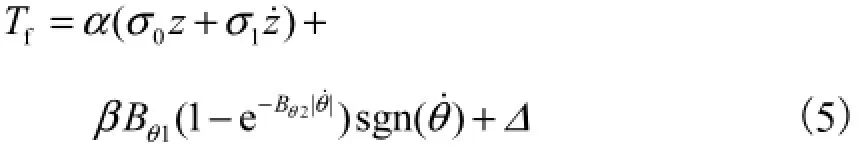
式中:α>0;β>0.当外部没有发生改变,且建模完全准确时,α=β=1且Δ=0,与原模型一致.
合并式(1)、(5),得到状态方程为
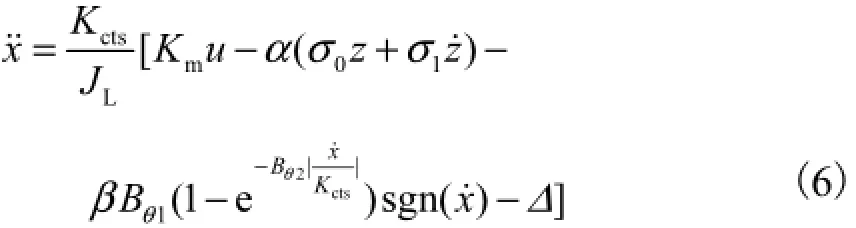
根据状态方程,即可采用反演设计方法进行自适应滑模摩擦补偿控制器的设计.
首先,良好的位置跟踪性能是伺服系统的控制目标,因此,将位置跟踪误差1e定义为第1个误差变量,即

设定稳定项为

式中c1为正实数.
设定Lyapunov函数1V为

并设定第2个误差变量2e
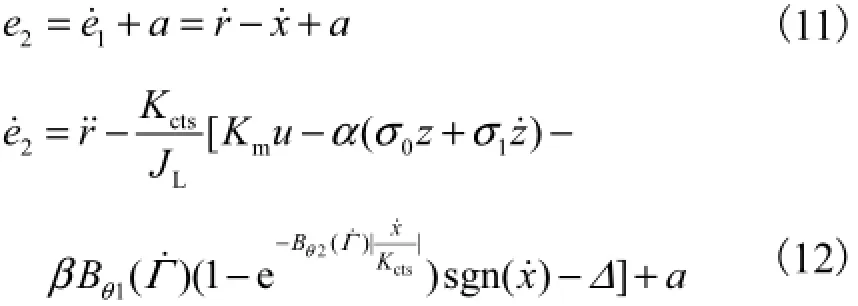
则有
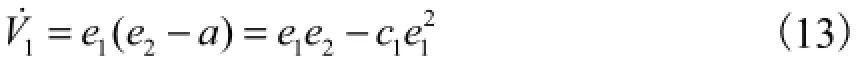
然后设定Lyapunov函数2V为

式中σ为滑模控制的切换函数.σ的定义为

式中k1为正实数.由此可得
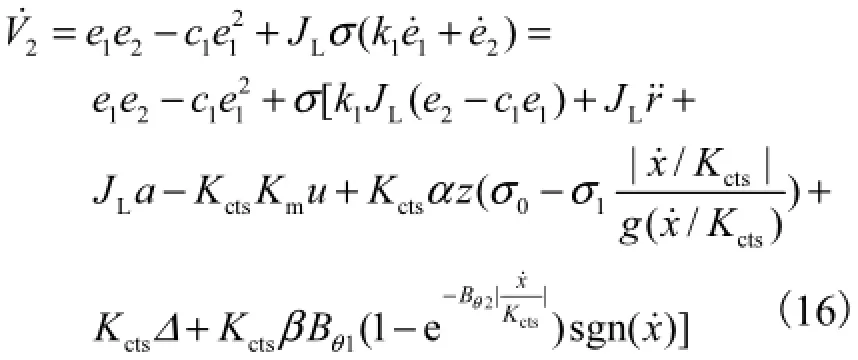
由于α、β和Δ为伺服系统中的不确定参数,直接根据式(16)设置滑模控制律,容易使系统出现抖振,因此,本文采用自适应方法对α、β和Δ进行估计.ˆα、ˆβ、ˆΔ分别为相应的估计值,则α、β和Δ的估计误差为
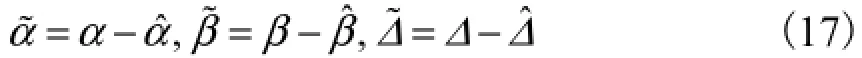
由于摩擦模型中的状态z是不可测的,因此需要利用非线性观测器进行估计,本文所采用的非线性观测器[3]为
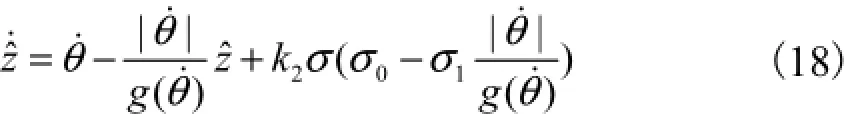
式中:ˆz为估计值;k2为正实数.设z~为其观测误差,则有
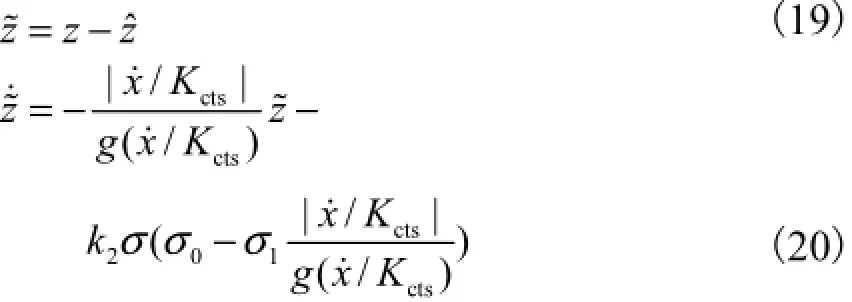
再设定Lyapunov函数3V为
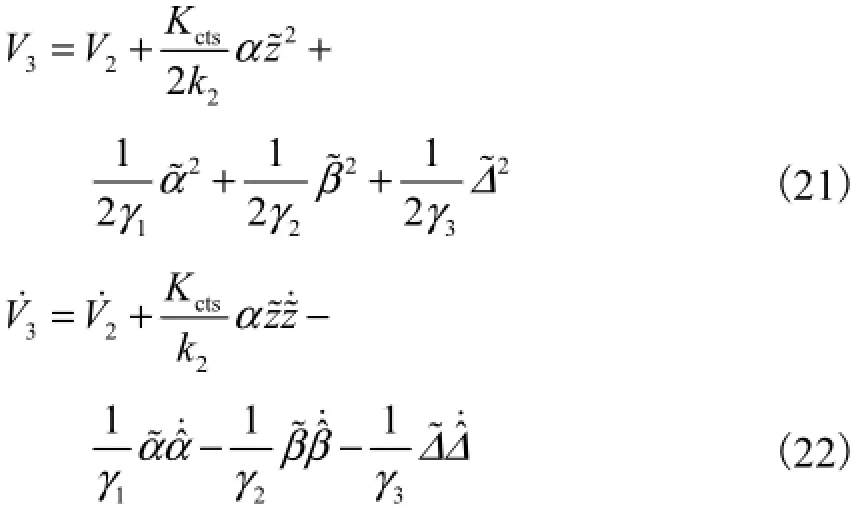
由于

将式(17)、式(20)、式(22)和式(23)结合,可得
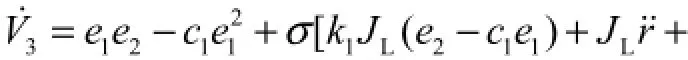
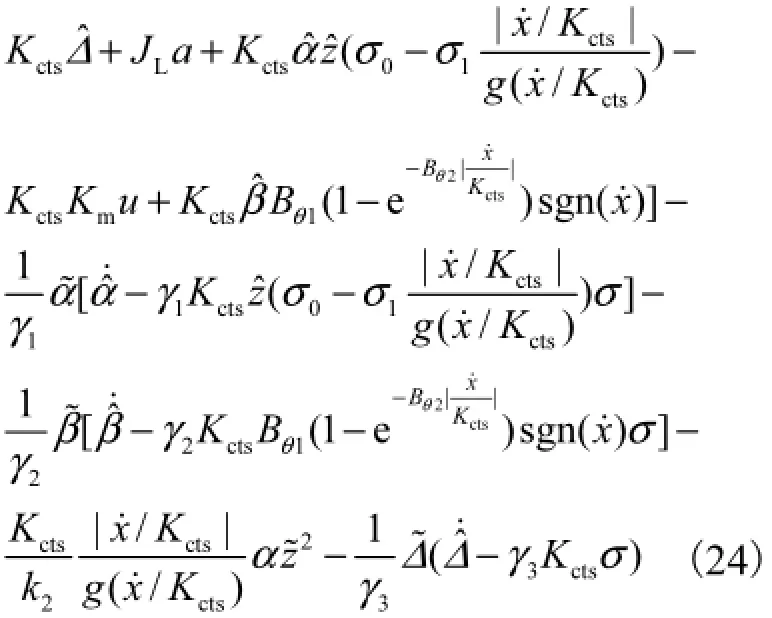
从而可根据式(17)进行自适应滑模控制器和自适应律的设计,即
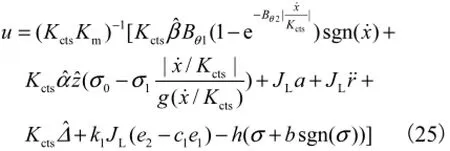
式中h和b为正实数.
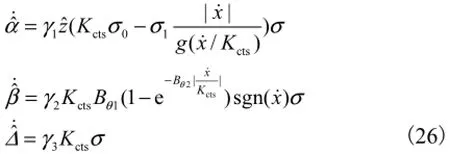
由此,建立了自适应滑模控制器,并确定了其切换函数、自适应律,以下分析系统的稳定性.
将式(25)和式(26)代入式(24),可得
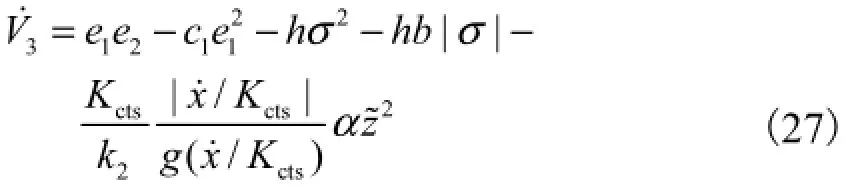
取
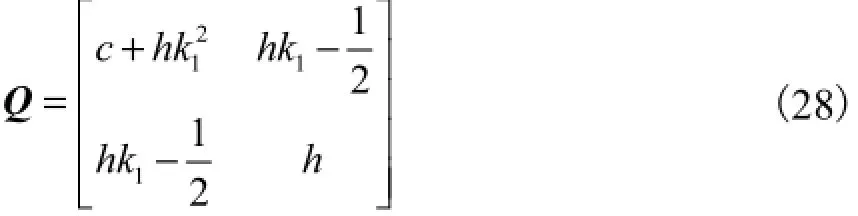
则有

因此
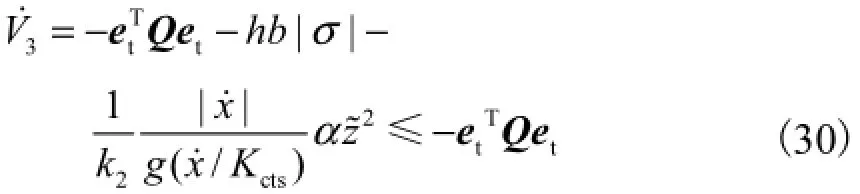
由于
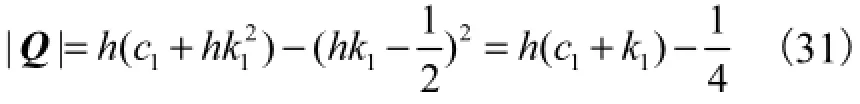
因此可通过设置h、c1及k1,使||Q>0,保证Q为正定矩阵,从而有

由此可知,本文设计的自适应滑模控制律在符合条件h( c1+k1)>1/4时,系统具有全局渐近稳定性.
4 补偿方案及实验
4.1 自适应滑模摩擦补偿方案
图3为自适应滑模摩擦补偿方案的控制框图,其中自适应滑模控制器的处理在PMAC中进行,控制器的输出u根据式(15)、式(25)和式(26)来确定.参数调试过程与PID调试类似,本文不再赘述.4.2 补偿实验
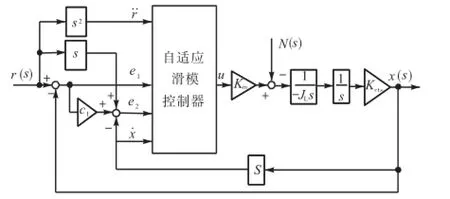
图3 自适应滑模摩擦补偿方案示意Fig.3Flow chart of adaptive sliding friction compensation scheme
为验证补偿方案的有效性,本文将以下两种补偿方案进行对比,一种是本文提出的自适应滑模摩擦补偿方案,一种是文献[3]提出的自适应摩擦补偿方案.在伺服平台连续运行1,h后,比较在正弦信号输入作用下的跟踪性能.
当输入正弦信号为r( t)=5sin(0.3πt)mm时,两种不同补偿方案下系统的跟踪误差如图4所示.
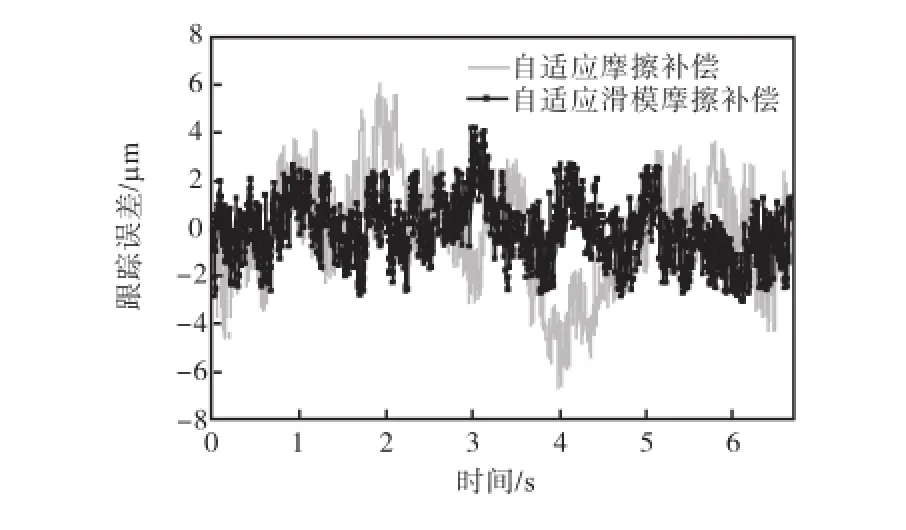
图4 正弦信号时的跟踪误差曲线Fig.4Curves of tracking error for a sinusoidal signal
由图4可知,采用自适应摩擦补偿时,系统的跟踪误差变动范围为±6.9,µm;而采用自适应滑模摩擦补偿时,系统的跟踪误差变动范围为±4.1,µm.
由此可知,由于自适应滑模摩擦补偿对系统中的不确定非线性建模误差和其他扰动也具有较强的抑制能力,因此相较于自适应摩擦补偿方案,能够更有效地提高伺服系统的控制精度.
5 结 论
(1) 本文根据反演设计思想,基于修正黏性摩擦的LuGre模型,提出了一种自适应滑模摩擦补偿控制器的设计方法.
(2) 利用PMAC的自定义伺服算法功能,在高精度开放式伺服平台完成了自适应滑模摩擦补偿.
(3) 采用自适应滑模摩擦补偿方案,系统的跟踪误差变动范围为±4.1,µm,明显优于采用自适应摩擦补偿方案时的±6.9,µm.
(4) 本文提出的自适应滑模摩擦补偿方案,解决了自适应补偿对未知建模误差和扰动的控制能力较弱的问题,又抑制了采用滑模控制出现的抖振现象,能够很好地实现伺服系统的位置逼近,控制精度较高.
[1] 向红标,裘祖荣,李醒飞,等. 测量机滚珠丝杠Z轴伺服系统的动力学建模及补偿[J]. 天津大学学报,2011,44(4):291-296.
Xiang Hongbiao,Qiu Zurong,Li Xingfei,et al. Dynamic modeling and compensation for the ball screw Z-axis servo system of measuring machine [J]. Journal of Tianjin University,2011,44(4):291-296(in Chinese).
[2] 孔祥臻,王 勇,蒋守勇. 基于Stribeck 模型的摩擦颤振补偿[J]. 机械工程学报,2010,46(5):68-73.
Kong Xiangzhen,Wang Yong,Jiang Shouyong. Friction chatter-compensation based on Stribeck model [J]. Journal of Mechanical Engineering,2010,46(5):68-73(in Chinese).
[3] 向红标,谭文斌,李醒飞,等. 基于LuGre模型的自适应摩擦补偿[J]. 机械工程学报,2012,48(17):70-74.
Xiang Hongbiao,Tan Wenbin,Li Xingfei,et al. Adaptive friction compensation based on LuGre model [J]. Journal of Mechanical Engineering,2012,48(17):70-74(in Chinese).
[4] Gilbart J W,Winston G C. Adaptive compensation for an optical tracking telescope[J]. Automatica,1974,10(2):125-131.
[5] 王发智,耿 蕊. 光电平台低速自适应摩擦补偿的研究[J]. 计算机仿真,2011,28(7):207-211.
Wang Fazhi,Geng Rui. Adaptive low velocity friction compensation for opto-electronic platform [J]. Computer Simulation,2011,28(7):207-211(in Chinese).
[6] Minh T N,Ohishi K,Takata M. Adaptive friction compensation design for submicrometer positioning of high precision stage[C]//International Congress of Mathematicians,IEEE. Kumamoto,Japan,2007:1-6.
[7] Reed J S,Ioannou Pa. Instability analysis and robust adaptive control of robotic manipulators[J]. IEEE Transactions on Robotics and Automation,1989,5(3):381-386.
[8] Sankaranarayanan S,Khorrami F. Model independent friction compensation[C]//American Control Conference,IEEE. Philadelphia,USA,1998,1:463-467.
[9] Young K D. A variable structure control approach to friction force compensation[C]//American Control Conference,IEEE. Philadelphia,USA,1998,4:2138-2142.
[10] 刘金琨. 滑模变结构控制MATLAB仿真[M]. 2版.北京:清华大学出版社,2012. Liu Jinkun. Sliding Mode Control Design and MATLAB Simulation[M]. 2nd ed. Beijing:Tsinghua University Press,2012(in Chinese).
[11] 谭文斌,李醒飞,向红标,等. 修正黏性摩擦的LuGre模型的摩擦补偿[J]. 天津大学学报,2012,45(9):824-828.
Tan Wenbin,Li Xingfei,Xiang Hongbiao,et al. Friction compensation based on LuGre model with modified viscous friction [J]. Journal of Tianjin University,2012,45(9):824-828(in Chinese).
(责任编辑:赵艳静)
Adaptive Sliding Friction Compensation Method Based on Modified LuGre Model
Tan Wenbin1,2,Li Xingfei1,Qiu Zurong1,Xiang Hongbiao3,Zhang Chenyang2
(1. State Key Laboratory of Precision Measuring Technology and Instruments,
Tianjin University,Tianjin 300072,China;2. School of Mechanical Engineering,Tianjin University of Commerce,Tianjin 300131,China;3. School of Mechanical Engineering,Tianjin University of Technology,Tianjin 300384,China)
In order to establish an open-servo system with good dynamic performance,this paper proposes a adaptive sliding mode compensation method based on modified viscous friction LuGre model. It is applied to solve the problem of adaptive friction compensation in unknown modeling errors and disturbance rejection. Firstly,a dynamic equation of an open-servo system is given and a servo system equation of state based on modified LuGre friction model is established. Secondly,according to the inversion design,an adaptive sliding friction controller,the corresponding adaptive laws and switching functions are given. Besides,its global asymptotic stability is analyzed by this method. In the last,a programmable multi-axis controller is utilized to realize the compensation applied to the open-servo platform and demonstrate the validity of the method. Results show that the tracking error of servo system is reduced from ±6.9,µm to ±4.1,µm compared with the conventional adaptive friction compensation,when the input signal is a sinusoidal signal. The proposed method effectively suppresses the adverse effects of friction and other uncertainties on the servo system and improves the tracking performance of the servo system.
LuGre model;adaptive sliding mode control;friction compensation
TP273;TH112
A
0493-2137(2015)05-0463-05
10.11784/tdxbz201311023
2013-11-08;
2014-04-30.
国家自然科学基金资助项目(50975206);精密测试技术及仪器国家重点实验室开放基金资助项目(PIL1302).
谭文斌(1984— ),男,博士,讲师,twb@tju.edu.cn.
李醒飞,lixf@tju.edu.cn.
时间:2014-05-08. 网络出版地址:http://www.cnki.net/kcms/doi/10.11784/tdxbz201311023.html.
