基于有限体积法的群桩绕流数值模拟
2015-06-05李绍武祁泽鹏
庄 茜,李绍武,祁泽鹏
基于有限体积法的群桩绕流数值模拟
庄 茜1,2,3,李绍武1,祁泽鹏1
(1. 天津大学水利工程仿真与安全国家重点实验室,天津 300072;2. 天津城建大学土木工程学院,天津 300384;3. 长沙理工大学水沙科学与水灾害防治湖南省重点实验室,长沙 410114)
采用COASTALTOOL软件中的潮流模块TC2D模拟桩绕流问题.通过细网格模型,研究桩断面形状、排列方式及桩心距对桩周围水流的影响.对于粗网格模型中群桩阻力的影响,提出基于阻力叠加原理的有桩单元水流阻力计算公式;对于单元中群桩的遮流作用,提出遮流面积折合水深的概化方法.这种概化计算模式中考虑了群桩中各桩间的遮蔽影响.
桩绕流;群桩阻力;遮流;概化
由群桩组成的透空式建筑物,对周围水流和泥沙运动的扰动要比实体墙建筑物小,在某些特定区域用做调整流场的工程措施往往具有一定优势,技术上需要根据群桩的阻流特性确定群桩布置方式和桩间距,理论上归结为孤立建筑物绕流问题.
物体绕流问题十分复杂,至今只能对简单、规则断面形状的圆桩或方桩在低雷诺数情况下给出解析解或半经验理论解.对于群桩阻流特性的问题需借助物理模型试验和数值计算.Zdravkovich[1]通过水槽试验,研究了两圆桩串列和交错放置,且桩心距小于5倍柱径时的绕流流场,结果表明,桩心距在3倍桩径是临界值,小于此值时,上游圆桩的涡尚未脱落,即进入第2个桩的影响范围;而超过此临界值时,上游桩后交替脱落的涡对下游桩的绕流力产生影响. Williamson[2]对两并列圆桩的绕流尾迹进行了研究,通过流场显示技术得到两圆桩的尾迹变化.李景银等[3]在低雷诺数下,在水槽中对4个正方形排列、桩间距为4倍桩径的圆桩进行了绕流试验,分别采用激光诱导荧光技术(LIF)和粒子成像测速(PIV)法测量了流场分布.邓绍云等[4-5]通过水槽试验,探讨了规则排列群桩的柱阻力系数随桩间距的变化.
在有网格数值模拟计算中,存在两种基本方法.一种是按单桩解析尺度进行网格剖分,进行原桩数值计算;另一种是采用较大网格,对单元内多个桩进行概化后计算.原桩计算的可以获得较高精度,但计算量大,概化计算的关键是如何对各桩的阻流效果进行合理概化.黄筱云等[6]采用自适应四叉树网格下的N-S方程数值求解圆桩绕流,其结果与前人试验结果一致.Stansby[7]用涡方法研究了双圆桩并排、串列、交错放置时的阻力特性,认为排列方式对阻力有影响.吴文权[8]通过数值计算研究了对称来流条件下多圆桩绕流问题,认为双圆桩绕流流动是双稳态的,多圆桩的排列方式对流场影响很大,前排对后排的影响尤为显著.Farrant等[9]用数值模拟方法研究了雷诺数Re=200时4个圆桩排列成正方形时的绕流问题,两桩间距分别为3倍和5倍桩径时,圆桩后方均出现旋涡脱落现象.张爱社等[10]用数值方法模拟了3圆桩布置成等边三角形时的二维绕流问题,得出各圆桩阻力系数和流场分布,结果表明,间距较小时3圆桩相互干扰,流动有偏向下游某个圆桩的倾向.唐士芳等[11-12]提出用折合底部摩阻力的经验方法来计算群桩绕流阻力,其中对于桩绕流阻力的处理缺乏明确的物理机制.解鸣晓等[13]提出在保证阻力等效的前提下以大尺度桩代替群桩的方法,概化中未考虑桩间影响.
本文首先通过细网格模型,研究不同桩断面、群桩排列方式及桩心距对桩周围水流的影响.对于粗网格模型中群桩的影响,提出一种综合考虑底部摩阻力与桩绕流阻力的理论公式和桩间遮流效果的概化方法,并通过对比细网格原桩模拟和粗网格概化模拟结果,验证该概化方法的有效性.
1 二维水流数学模型
运用自行开发的海岸软件COASTALTOOL中的二维潮流模块TC2D进行水流数值计算,模型的基本方程及求解方法概述如下.
1.1 控制方程
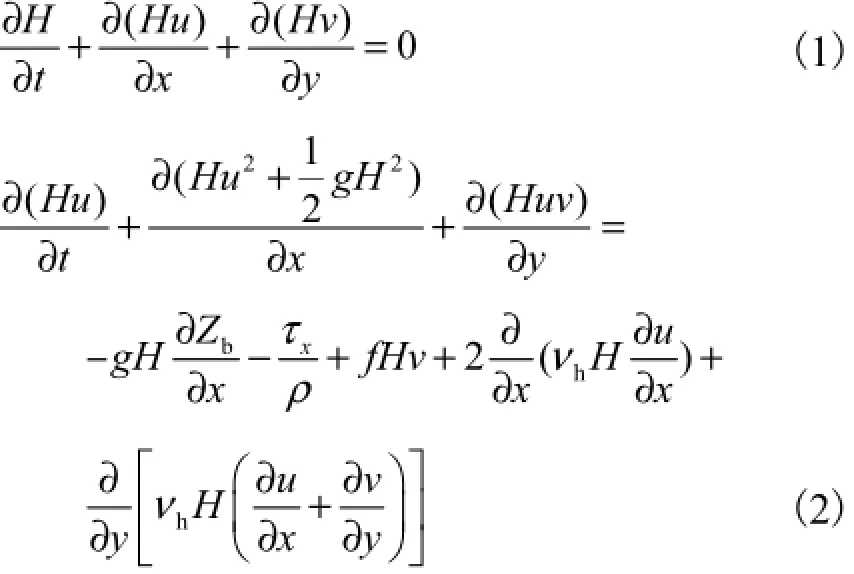
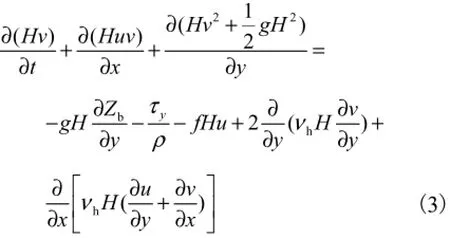
在如图1所示的坐标系下,浅水波运动方程为式中:H为全水深,H=η-Zb,η为水位,Zb为底高程;u、v分别为x、y方向上的流速分量;g为重力加速度;τx、τy分别为水流阻力在x、y方向的分量;ρ为水的密度;f为Coriolis频率参数,为地球自转频率,为当地纬度;νh为水平方向的紊动黏滞系数,采用Smagorinsky亚格子紊动模型计算,即
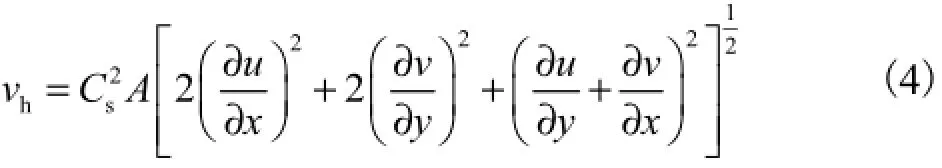
式中:Cs为系数,取0.1~0.2;A为单元面积.
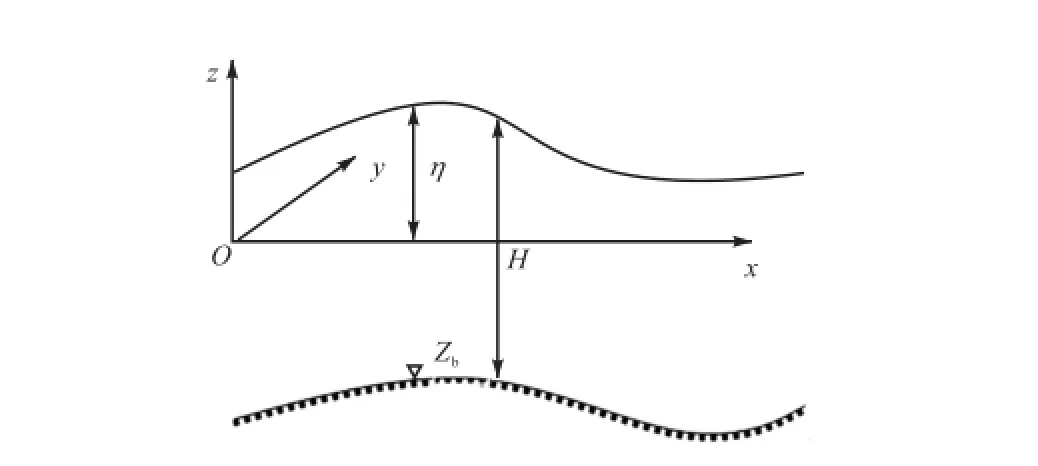
图1 坐标系示意Fig.1 Sketch of coordinate system
1.2 边界条件
开边界处给水位过程.水平方向固边界采用“不穿透”条件,沿固边界的法向分量恒为零,即

式中:v为流速矢量;n为固边界的单位外法线矢量.
1.3 控制方程的数值求解方法
采用三角形和四边形混合单元,以提高计算效率.离散变量定义在各单元的中心,单元交界处变量产生间断,交界面数值通量采用Osher格式计算,有关方程离散过程详见文献[14].
1.4 群桩概化方法
将群桩所在单元视为水单元,采用等效阻力系数和等效过水面积相结合的方法对群桩进行概化,具体方法如下.
1.4.1 单元综合水流阻力
单元内有桩时,单元综合水流阻力可视为底部摩阻力与桩绕流阻力之和,即

式中:Ai为第i个单元的面积;wiT和piT分别为底部摩阻力和桩绕流阻力.底部摩阻力wiT的表达式为
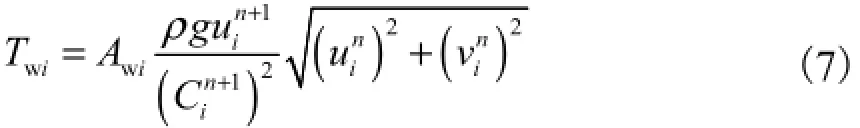
式中:Awi为扣除桩位后单元i的面积;C为谢才系数,可用曼宁公式计算;上标n表示时间层.
桩绕流阻力piT为单元中各桩绕流阻力之和,即
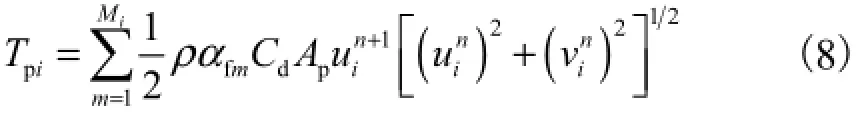
式中:Mi为单元i内桩的个数;αfm为考虑群桩内各桩相互影响后的绕流阻力校正系数,根据文献[5]和笔者的大量数值研究结果,αfm与桩的排列方式、桩心距等因素有关,其值取决于各桩对综合阻力的贡献,可根据试验结果或数值试验结果选取;Cd为单桩绕流阻力系数;Ap为单桩在水流方向投影的面积,为单桩在水流方向投影的宽度为第i单元的自然水深.
假设单元内桩尺寸统一,离散方程中的x向单元综合水流阻力分量可表示为
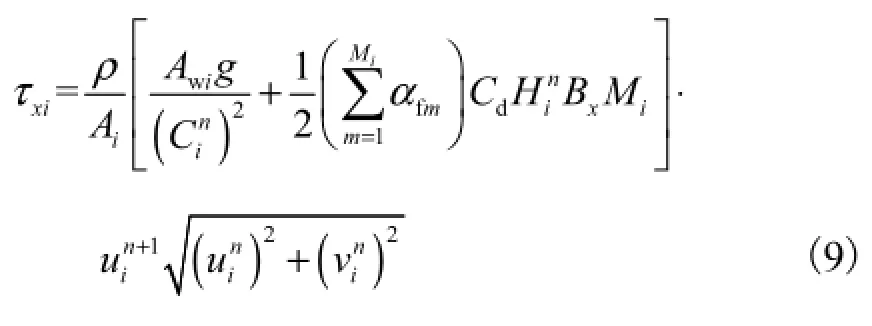
y方向单元综合水流阻力分量可表示为
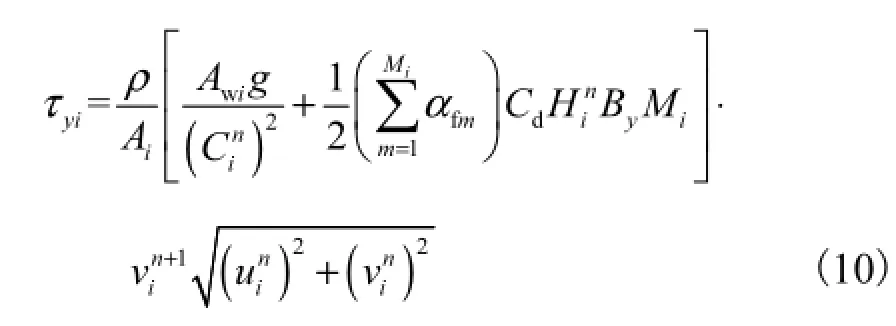
1.4.2 过水面积等效
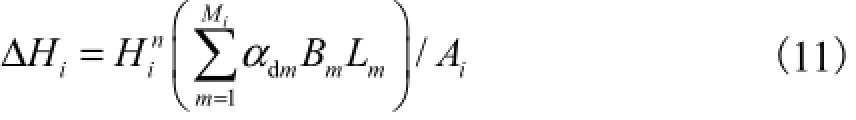
群桩不但增加了水流阻力,也改变了局部过水面积.过水面积等效是将单元中桩群遮挡的过水面积折合成垂向高度,在单元水深中予以扣除.需扣除的折合水深计算公式为式中:αdm为考虑桩间遮蔽作用的调整系数;Lm为第i单元中第m根桩在单元中沿水流方向影响域的长度(见图2);Bm为第i个单元中第m根桩在单元中沿水流方向的影响域的宽度.
遮蔽调整系数αdm的取值目前尚无理论方法.从工程实用角度,初步可按如下方法取值.若单元内沿水流方向单桩或并列多根桩时αdm取1;若横向多根桩不并列(错位布置),则对位于上游的首个桩αdm取1,其后的桩则根据文献[1, 9-10]中有关前桩对后桩的影响仅限于其后3倍桩径D范围的结论,按式αdm=min(δ/3D,1)计算,其中δ 为前、后桩在水流方向投影距离.往复流可按不同方向算出的折合水深中最不利方向考虑.
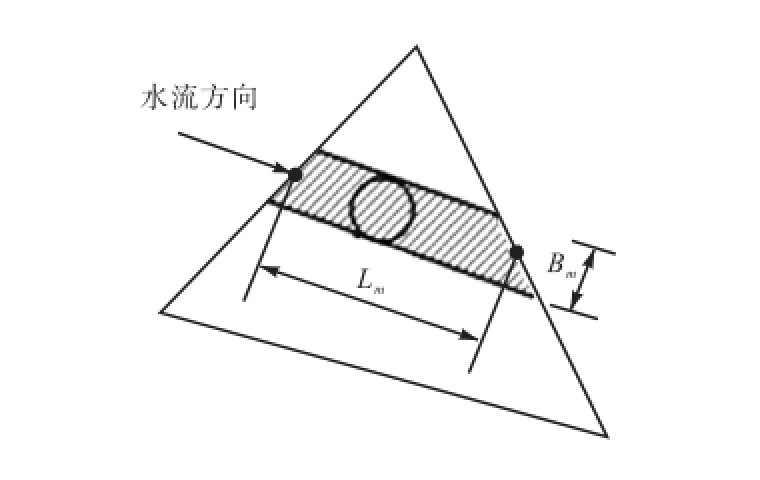
图2 桩在单元中沿水流方向影响域示意Fig.2Sketch of influence domain of pile in an element along flow direction
2 模型有效性验证
采用Roulund等[15]的水槽试验资料对二维水流数学模型的有效性进行检验.试验为单个圆桩绕流问题.数值水槽长1,000,m,宽200,m,纵比降为1.17/10,000,底部糙率与物模一致,取0.022.水深为0.54,m,圆桩直径为0.536,m,置于水槽横断面中心,均匀流流速为0.326,m/s,桩雷诺数为1.75×105.采用三角形网格,桩附近进行网格加密(见图3).计算区域左端为来流边界,右端为出流边界,上、下侧均为滑移固边界.
桩前、后垂向平均流速模拟结果与实测结果对比如图4所示,桩前模拟结果与实测结果符合很好,桩后实测值呈现先增大、再减小、而后又增大的过程,这可能是由于桩后1倍D范围内为尾流区,涡动使得流场变化复杂,故二维模型无法准确模拟桩后较近范围内的复杂流场,但在尾流区以外的计算结果与实测结果是吻合的.
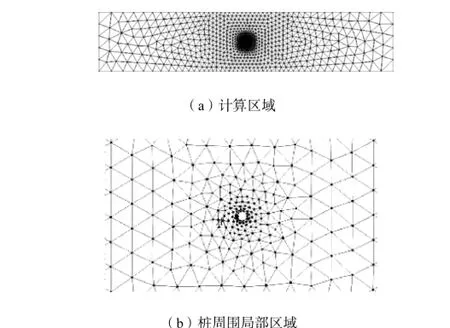
图3 圆桩绕流计算区域及网格划分Fig.3 Computational domain and mesh discretization of flow around cylindrical pile
根据伯努利方程导出桩前水位壅高/Z DΔ的计算公式为

式中Fr为弗劳德数.
仍采用上述数值水槽,计算条件如表1所示.驻点A处(见图3)相对水位壅高/Z DΔ随弗劳德数Fr变化的模拟结果与伯努利方程理论结果对比如图5所示,可以看出二者十分吻合.
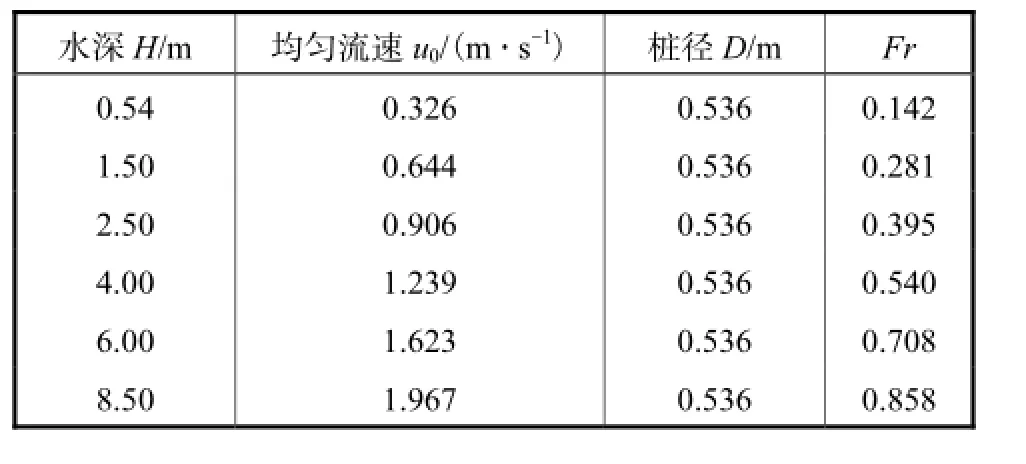
表1 模型计算条件Tab.1 Computational conditions of model
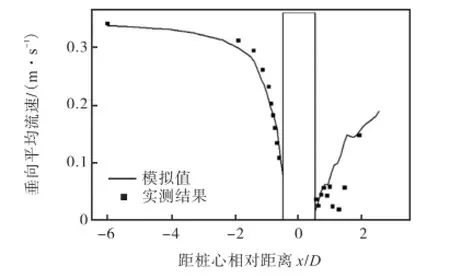
图4 垂向平均流速模拟结果与实测结果对比Fig.4 Comparison of mean vertical velocity between numerical simulation and measurement results
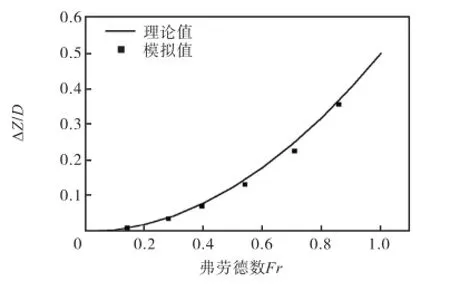
图5 桩前水位壅高值模拟结果与理论结果对比Fig.5Comparison of water level rising in front of the pile between numerical simulation and theoretical results
3 断面形状对绕流流场的影响
建立20,000,m×18.6,m的矩形数值水槽,计算区域左端为来流边界,右端为出流边界,上、下侧均为滑移固边界.底坡J=1/100,000,槽底糙率0.015,水深20,m.均匀流流速为u0=1.55,m/s.分别模拟断面形状为圆形(D=0.6,m)、正方形(边长L=0.6,m)和正菱形(对角线长B=0.6,m)的桩的绕流流态.桩置于水槽中心(见图6),计算区域及网格划分见图7.
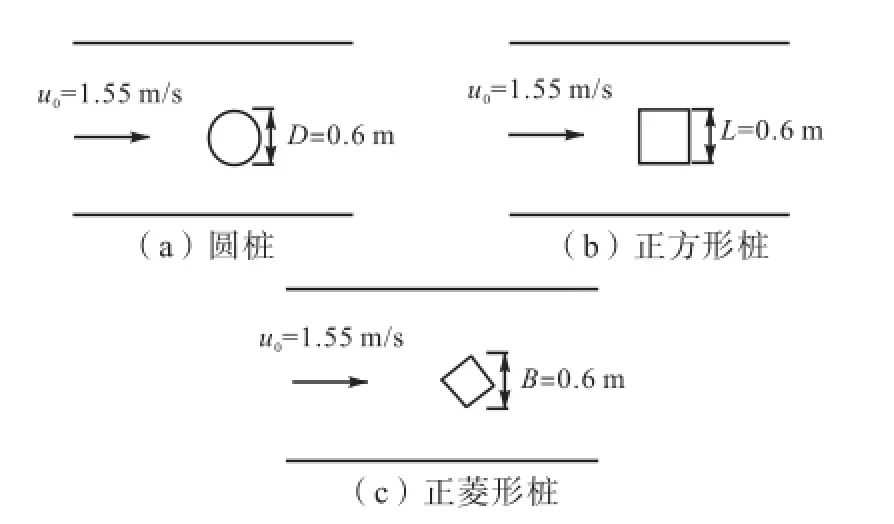
图6 不同断面形状桩绕流平面布置示意Fig.6Sketch of plane layout of flow around piles with different cross sections
不同断面形状桩的流速场模拟结果对比如图8所示,水位模拟结果对比如图9所示,横断面与纵剖面流速u与平均流流速u0之比u/u0的计算结果对比如图10所示,横断面与纵剖面水位变化相对值(HH0)/D计算结果对比如图11所示.从结果可以看出,在横向上,圆桩与正方形桩及正菱形桩的流速分布不同,贴近桩体处圆桩流速最大,但随后有所下降,在远离桩体处圆桩的流速最小.正方形桩与正菱形桩相比,由于断面形状略大,对水流的挤压作用也略大.从纵向看,正菱形桩后流速最小,圆桩与正方形桩后的流速较接近,表明其阻流效果好于圆桩和正方形桩.原因与正菱形桩的形状有关.
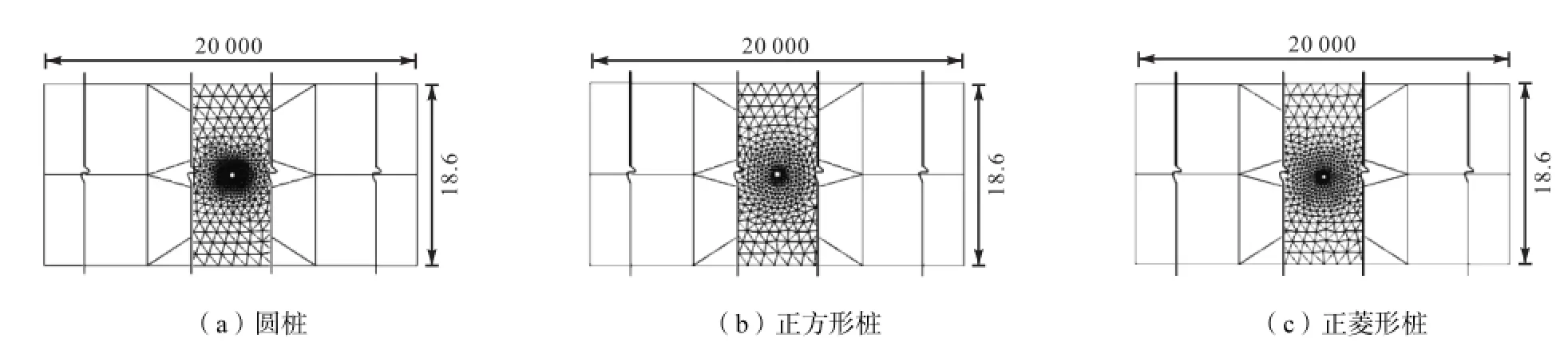
图7 不同断面形状的桩绕流计算区域及网格划分(单位:m)Fig.7 Computational domain and mesh discretization of flow around piles with different cross setions(unit:m)
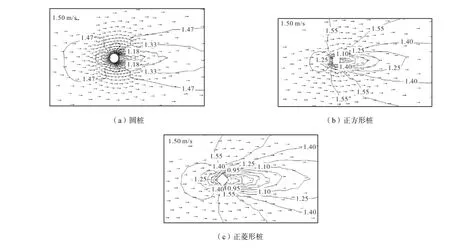
图8 不同断面形状桩的流速场模拟结果对比(单位:m/s) Fig.8 Comparison of simulation results of flow velocity field for piles with different cross sections(unit:m/s)
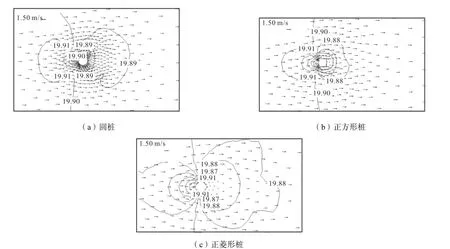
图9 不同断面形状桩的水位模拟结果对比(单位:m)Fig.9 Comparison of simulation results of water surface elevation for piles with different cross sections(unit:m)
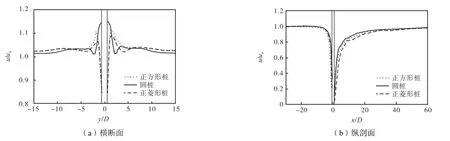
图10 不同断面形状的桩绕流u/u0计算结果对比Fig.10 Comparison of u/u0of flow around piles with different cross sections
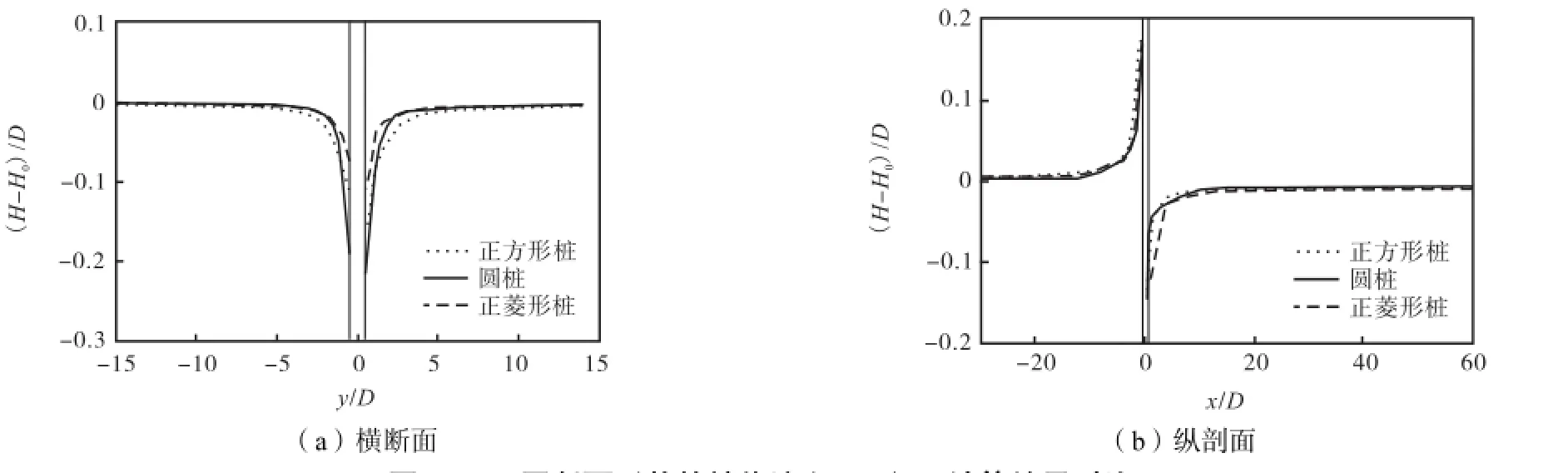
图11 不同断面形状的桩绕流(H-H0)/D计算结果对比Fig.11 Comparison of (H-H0)/D of flow around piles with different cross sections
4 透空式阻流堤阻流效果讨论
工程中直接采用不透水堤来调整流速和流态往往会引起局部水流的剧烈改变,给工程带来各种不利影响,如由于流速剧烈改变引起泥沙回淤或局部流速过大造成船舶航行或靠泊困难等.而采用透空式群桩阻流堤既可以达到调整流速的目的,又不至于引起当地流场的剧烈改变,作用效果比较和缓,但为了确定合理的群桩布置方案,需要了解群桩阻流效果.以下针对不同排列形式的桩排,研究其阻流效果.
选择单排并列、两排并列和3排并列3种布置形式进行研究,其中堤长按10根桩并列考虑.
为了严格控制水位和流速条件,数值水槽的上下游开边界均给恒定水位.流速初值赋0.经试算,达到指定流速值需要的水槽长度应大于500,km,故实际取500,km,水槽宽100.8,m.水槽两侧边界设置为自由滑移边界.底坡J=1/100,000,水深20,m,槽底糙率0.015,均匀流流速u0=1.55,m/s.桩横断面选择直径D=0.6,m的圆桩和边长L=0.6,m的方桩进行对比,横向、纵向桩心距SH=SV变化范围为(2~4)D(L).为了减少网格数量,桩的上下游两侧大部分区域均采用矩形网格,桩周围采用三角形网格,之间平滑过渡(见图12).多排桩按等间距梅花排列,见图13.
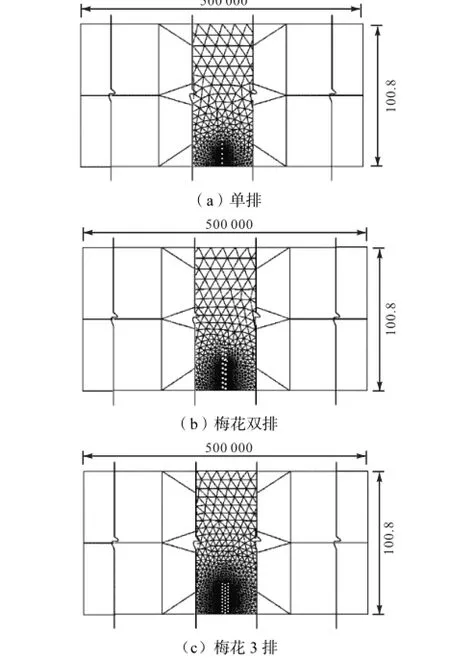
图12 圆桩桩排计算区域及网格划分示意(单位:m)Fig.12Computational domain and mesh discretization of cylindrical pile rows(unit:m)
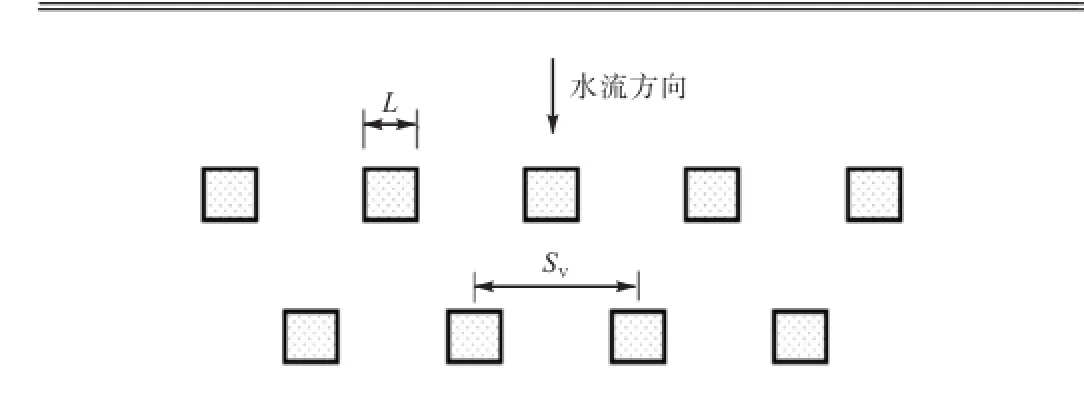
图13 梅花排列示意Fig.13 Sketch of staggered array of pile group
由计算结果统计各种布置方式桩后(30~200)· D(L)处流速折减率处为上限,200,D(L)处为下限)、堤长及百米桩数如表2所示.图14和图15分别给出了圆桩和方桩在不同桩心距和排列情况下桩后不同位置处流速相对值的横向分布结果,图中y为沿桩排轴线方向坐标,y/D为相对距离.可以看出,方桩的阻流效果略好于圆桩.
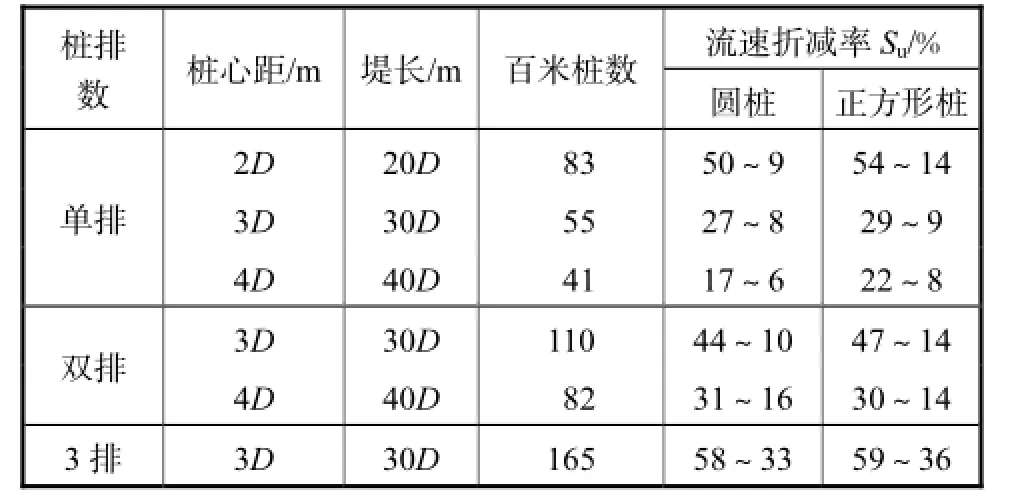
表2 不同桩心距和排列群桩阻流堤后阻流效果数值模拟结果Tab.2Simulation results of the resistance effect in the rear side of pile-group with different spacings and array layouts
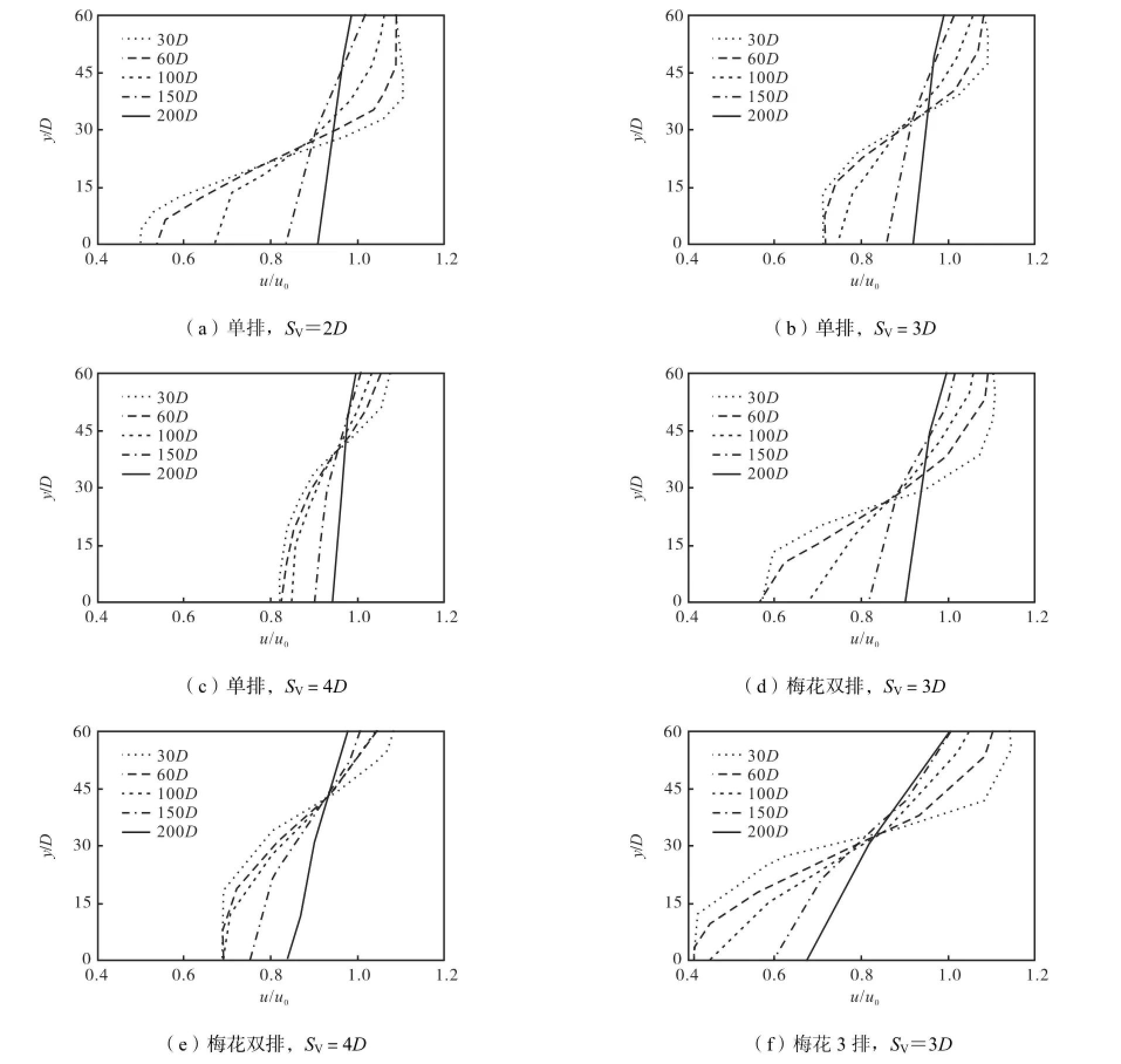
图14 不同桩间距和排列圆桩的阻流效果Fig.14 Resistance effect of cylindrical pile group with different spacings and array layouts
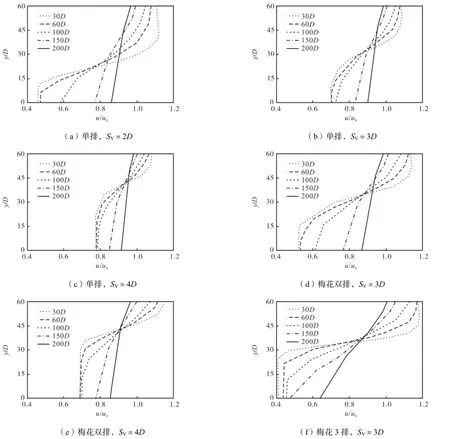
图15 不同桩心距和排列方桩的阻流效果Fig.15 Resistance effect of square pile group with different spacings and array layouts
5 群桩概化模拟
某码头为高桩墩式结构,码头轴线与流场中最大流速方向呈17°角,码头由17个墩台构成,考虑到计算工作量,本研究暂模拟其东端4个墩台.墩台尺寸为31,m×26,m,由39根直径D=1.4,m、不规则排列的圆桩(见图16)支撑.
矩形数值水槽长40,000,m、宽1,000,m.群桩位于水槽中央,水槽上下两侧为固边界,与群桩有足够的间距,水槽左、右端为开边界.水槽底坡J=1/100,000,水深25,m,槽底糙率0.015,均匀流流速u0=1.80,m/s.

图16 码头群桩平面布置及群桩周围细网格剖分Fig.16Plane layout of pile group of wharf and fine mesh discretization
模拟分为直接和概化两种情况.直接模拟是将单桩外轮廓当作固边界对计算区域进行剖分(见图16),而概化模拟是将整个墩台范围划分为8个单元
(见图17),群桩不等距分布在8个单元中(见图18). 直接模拟单元总数为24,564,计算时间步长为0.01,s,概化模拟单元总数为1,852,计算时间步长为0.3,s.概化模拟计算量相当于直接模拟计算量的近1/400,计算效率大大提高.
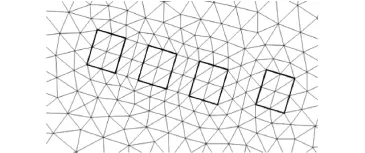
图17 群桩概化模拟粗网格剖分Fig.17 Coarse mesh for simplification simulation of pile group
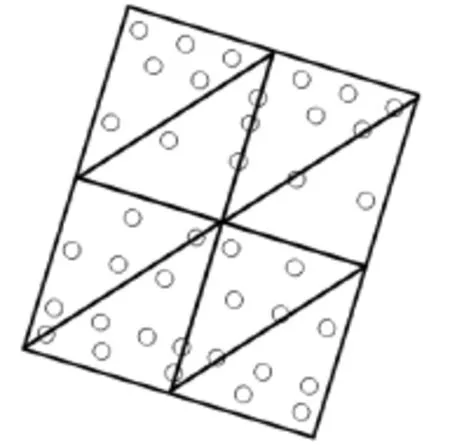
图18 概化模型中群桩分布Fig.18 Real pile group array of simplification model
从解决工程问题的角度出发,概化模拟中把不规则排列的39根桩简化成40根8×5矩形排列的群桩,横向桩心距SH=3D,纵向桩心距SV=4D.根据笔者利用计算流体力学软件FLUNET对不同桩数和桩间距的矩形排列群桩阻力系数进行数值模拟计算的结果[16],本算例中绕流阻力校正系数取40根桩分布在8个单元中,每个单元中有5根桩,群桩所在单元绕流阻力校正系数.根据桩的雷诺数,单桩阻力系数取0.4.
群桩所在单元面积为101,m2,阻流面积为95,m2,由式(11)算得折合水深ΔHt=23.5 m.
桩群概化模拟与直接模拟流场分布对比如图19所示,图中Δh为群桩引起的水位变化,负号表示水位降低.可以看出,二者流速是相符的,水位误差在2%~5%.结果表明,这种考虑群桩阻力和遮流效果的概化方法既可有效提高计算效率,又有较好的计算精度.
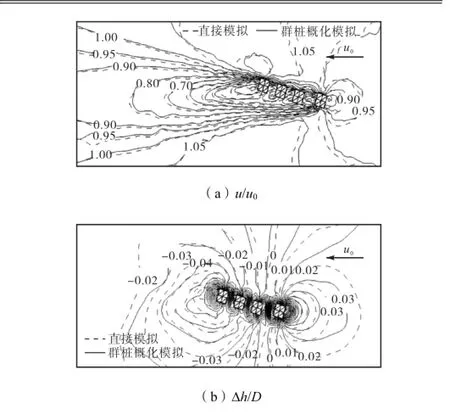
图19 群桩概化与直接模拟流场分布对比Fig.19Comparison of the flow field of simplification simulation for pile group against direct simulation
6 结 论
(1) 采用COASTALTOOL海岸软件中的潮流模块TC2D模拟了桩绕流问题,结果表明桩前水位壅高计算结果与理论值吻合较好,流速和水槽试验实测结果一致,桩后较小范围内的复杂流场模拟结果略差,但尾流区以外计算结果与试验结果是吻合的.
(2) 通过对比不同断面形状的桩绕流模拟结果发现,在横向上圆桩对水流的挤压效果最明显,而在纵向上正菱形桩的阻流效果好于圆桩和正方形桩,这应与桩的断面形状有关.
(3) 提出了考虑底部摩阻力及桩群绕流阻力的综合阻力计算公式,公式考虑了群桩中各桩间的遮蔽作用;提出了初步考虑桩间相互影响的群桩概化方法. 群桩概化与直接模拟结果的对比表明,本文提出的群桩计算概化模式具有较好的精度.
(4) 研究了透空式群桩阻流堤断面形状、排列方式以及桩心距等因素对阻流效果的影响,得到了不同排列群桩后的流速折减率,结果表明正方形桩的阻流效果略好于圆桩.
[1] Zdravkovich M M. Review of flow interference between two circular cylinders in various arrangements[J]. Journal of Fluids Engineering,1977,99(4):618-633.
[2] Williamson C H K. Evolution of a single wake behind apair of bluff bodies[J]. Journal of Fluid Mechanics,1985,159(1):l-18.
[3] 李景银,Lam K,Chan K T,等. 绕正方形排列的顺排的四个圆柱的流动研究[J]. 工程热物理学报,2004,25(1):59-62.
Li Jingyin,Lam K,Chan K T,et al. Stydy on the cross flow around four cylinders in an in-line square arrangement at low Reynolds numbers[J]. Journal of Engineering Thermophysics,2004,25(1):59-62(in Chinese).
[4] 邓绍云,张嘉利. 桩群阻力测试的研究[J]. 华北水利水电学院学报,2007,28(2):86-90.
Deng Shaoyun,Zhang Jiali. Study on experiment of testing for drag force of water flow around groups of piles[J]. Journal of North China Institute of Water Conservancy and Hydroelectric Power,2007,28(2):86-90(in Chinese).
[5] 邓绍云. 桩柱水流绕流阻力特性及其计算[J]. 中国港湾建设,2007(1):14-21.
Deng Shaoyun. Drag force characteristics and calculation of water flow around pile[J]. China Harbour Engineering,2007(1):14-21(in Chinese).
[6] 黄筱云,李绍武. 自适应四叉树网格下的N-S方程数值求解模型[J]. 天津大学学报:自然科学与工程技术版,2013,46(1):58-66.
Huang Xiaoyun,Li Shaowu. Numerical N-S equation solver based on adaptive ouadtree mesh[J]. Journal of Tianjin University:Science and Technology,2013,46(1):58-66(in Chinese).
[7] Stansby P K. A numerical study of vortex shedding from one and two circular cylinders[J]. Aeronautical Quarterly,1981,32(1):48-71.
[8] 吴文权. 流体绕多个钝体不稳定分离流动数值仿真[J]. 华东工业大学学报,1997,19(3):1-8.
Wu Wenquan. Numerical simulation for unstable separated flow past multi-blunts[J]. Journal of Huadong Poly-technic University,1997,19(3):1-8(in Chinese).
[9] Farrant T,Tan M,Price W G. A cell boundary element method applied to laminar vortex-shedding from arrays of cylinder in various arrangements[J]. Journal of Fluids and Structures,2000,14(3):375-402.
[10] 张爱社,张 陵. 等边布置三圆桩绕流的数值分析[J]. 应用力学学报,2003,20(l):142-150.
Zhang Aishe,Zhang Ling. Numerical simulation of three equispace dcircular cylinders[J]. Chinese Journal of Applied Mechanics,2003,20(l):142-150(in Chinese).
[11] 唐士芳. 二维潮流数值水槽的桩群数值模拟[J]. 中国港湾建设,2002,6(3):14-21.
Tang Shifang. Numerical simulation for pile group innumerical water flume of two dimensional tidal flow[J]. China Harbour Engineering,2002,6(3):14-21(in Chinese).
[12] 唐士芳,李 蓓. 桩群阻力影响下的潮流数值模拟研究[J]. 中国港湾建设,2001,10(5):25-29.
Tang Shifang,Li Pei. Study on numerical simulation of tidal flow influenced by pile group resistance[J]. China Harbour Engineering,2001,10(5):25-29(in Chinese).
[13] 解鸣晓,张 玮,谢慧姣. 桩群数值模拟中的概化方法研究[J]. 水动力学研究与进展,2008,A23(4):464-471.
Xie Mingxiao,Zhang Wei,Xie Huijiao. Simplification method in numerical modeling of bridge pier group[J]. Chinese Journal of Hydrodynamics,2008,A23(4):464-471(in Chinese).
[14] 李绍武,卢丽峰,时 钟. 河口准三维涌潮数学模型研究[J]. 水动力学研究与进展,2004,A19(4):407-415.
Li Shaowu,Lu Lifeng,Shi Zhong. A quasi-3D numerical model for estuarinetidal bore[J]. Chinese Journal of Hydrodynamics,2004,A19(4):407-415(in Chinese).
[15] Roulund A,Sumer B M,Fredsøe J,et al. Numerical and experimental investigation of flow and scour around a circular pile[J]. Journal of Fluid Mechanics,2005,534:351-401.
[16] 庄 茜. 建筑物绕流数学模型理论及应用研究[D]. 天津:天津大学建筑工程学院,2013.
Zhuang Qian. Study on Theory and Application of Mathematical Model for Flow Around Structures[D]. Tianjin:School of Civil Engineering,Tianjin University,2013(in Chinese).
(责任编辑:樊素英)
Numerical Simulation for Flow Around Pile Group Based on FVM
Zhuang Qian1,2,3,Li Shaowu1,Qi Zepeng1
(1. State Key Laboratory of Hydraulic Engineering Simulation and Safety,Tianjin University,Tianjin 300072,China;2. School of Civil Engineering,Tianjin Chengjian University,Tianjin 300384,China;3. Key Laboratory of Water and Sediment Science and Water Hazard Prevention,Changsha 410114,China)
Flow around pile is studied by using the tide module TC2D of COASTALTOOL software. The effects of pile transection shape,array layout and center distance of pile group on the flow around piles are investigated,respectively,by adopting fine grid model. As for the coarse grid model,a calculation formula is proposed for the resistance of pile group inside an element based on the superposition principle of resistance. A simplification method is put forward to account for the shielding effect of pile group in an element by introducing the equivalent water depth for the sheltered area of the piles,by which the shielding effect among piles of a pile group is considered.
flow around pile;resistance of pile group;shielding effect;simplification
TV131
A
0493-2137(2015)05-0445-10
10.11784/tdxbz201403091
2014-03-27;
2014-09-29.
国家自然科学基金资助项目(51379143);国家创新研究群体基金资助项目(51021004);水沙科学与水灾害防治湖南省重点实验室基金资助项目(2014SS01).
庄 茜(1980— ),女,博士研究生,讲师,zq@tcu.edu.cn.
李绍武,lishaowu@tju.edu.cn.
