基于Hillinger-Reissner变分的混合单元的开发与应用

丁 阳，赖程钢，李 宁，李忠献

基于Hillinger-Reissner变分的混合单元的开发与应用

丁 阳1,2，赖程钢1，李 宁1,2，李忠献1,2

(1. 天津大学建筑工程学院，天津 300072；
2. 天津大学滨海土木工程结构与安全教育部重点实验室，天津 300072)

基于Hellinger-Reissner变分建立了一种用于几何和材料非线性分析的混合单元，采用位移形函数和考虑二阶效应的内力形函数对截面位移和截面内力进行插值，建立混合控制微分方程；通过静力凝聚消除单元节点力未知量得到单元刚度矩阵和单元内力．单元状态确定过程中，截面层次的平衡方程和单元层次的协调方程均通过引入非线性迭代算法以消除残余误差，从而减少结构层次的迭代次数．混合单元结合纤维截面模型用于钢管混凝土(CFST)构件的数值分析，结果表明：相对于刚度法和柔度法单元，基于Hellinger-Reissner变分的混合单元可以更加准确地反映构件的几何和材料非线性，非线性迭代算法用于单元状态确定具有良好的计算效率和数值稳定性．在此基础上对影响CFST构件几何非线性的主要参数进行了分析．

Hellinger-Reissner变分；混合单元；非线性迭代；几何非线性；材料非线性；钢管混凝土(CFST)

随着工程结构复杂程度增大，结构非线性分析日渐发挥重要功能，广泛应用于工程和研究领域．近年来，如何提高梁柱单元在结构几何、材料非线性问题求解中的分析精度和计算效率一直是研究者关注的热点问题之一．

基于纤维截面模型的分布塑性梁柱单元可准确地反映轴力和弯矩共同作用下材料的非线性，具有良好的分析精度和计算效率．然而，对于大变形状态下的几何非线性，一直未能得到很好的解决．

聂建国等[1]基于有限元程序MSC.MARC开发了用于组合结构地震反应分析的刚度法纤维梁单元；王文达等[2]基于非线性纤维梁-柱理论建立了分布塑性有限元模型，用于钢管混凝土(concrete filled steel tube，CFST)框架结构全过程分析．传统的刚度法单元采用三次横向位移和线性轴向位移假定，适用于线性曲率和轴向常应变位移场，无法准确描述构件在强非线性状态下的真实位移场分布形式．通过增加单元数量或者采用更高阶形函数[3-4]来逼近真实位移场可以提高计算精度，但将影响单元计算效率．

相对于刚度法单元，柔度法单元以节点力作为基本未知量，沿构件全长插值得到截面内力，严格满足单元平衡方程．但是现有的有限元程序中柔度法单元均为几何线性单元，基于小变形假定建立单元控制方程，无法考虑构件在大变形下的几何非线性．针对这一问题，陈滔等[5-6]结合二阶柔度法和纤维模型梁柱单元，在内力形函数中引入横向位移考虑构件二阶效应．文献[7-9]基于Hillinger-Reissner变分提出了考虑几何非线性的分析方法，以单元节点位移和节点力作为基本未知量通过位移形函数和内力形函数插值得到截面位移和截面内力，最终通过静力凝聚消除节点力未知量得到单元刚度矩阵．该方法基于两场变分能够较为准确地反映构件在大变形状态下的受力状态，并且相对柔度法单元在数值计算上具有更好的稳定性．

本文在已有研究基础上，基于Hellinger-Reissner变分建立混合单元有限元方程，将非线性迭代算法用于截面层次和单元层次消除残余误差，从而减少结构层次迭代次数．将混合单元结合纤维截面模型嵌入开源有限元程序OpenSees用于钢管混凝土构件非线性分析，以充分验证混合单元以及非线性迭代算法用于非线性分析的有效性．基于混合单元分析了构件长细比和荷载偏心比对钢管混凝土构件几何非线性的影响规律．

1 基于Hillinger-Reissner变分的混合单元

图1给出了混合单元有限元方程建立的流程.混合单元以节点位移和节点力作为基本未知量，分别通过位移形函数和内力形函数插值得到截面位移和截面内力，由截面位移得到的截面应变与由截面内力得到的截面应变之间应满足协调方程；截面内力和外荷载之间应满足单元平衡方程；最终由单元平衡方程和协调方程基于Hellinger-Reissner变分建立单元刚度矩阵．单元状态确定过程中，由节点力插值得到的截面内力与由截面应变积分得到的截面内力尚需满足截面平衡方程．

混合单元基于以下基本假定：①不考虑剪切和扭转变形的影响；②单元截面应变状态符合平截面假定；③单元外荷载只考虑杆端集中荷载；④单元轴向变形满足小变形假定．

1.1 单元力与变形

混合单元基本未知量包括单元节点位移向量U和节点力向量Q，即

式中：ΔL为杆端相对轴向变形；θzi、θzj为绕z轴的杆端转角；θyi、θyj为绕y轴的杆端转角；Nx为杆端轴力；Mzi、Mzj为绕z轴的杆端弯矩；Myi、Myj为绕y轴的杆端弯矩．

单元轴向位移和横向位移分别采用线性形函数和三次Hermitian形函数，截面位移向量u可以表示为

式中：u(x)为截面轴向位移；v(x)、w(x)分别为截面2个主轴方向上的横向位移；Nu为单元位移形函数矩阵．

为描述单元应变与位移的非线性关系，由单元截面位移向量u得到的截面应变向量d采用Green-Lagrange应变张量表示为

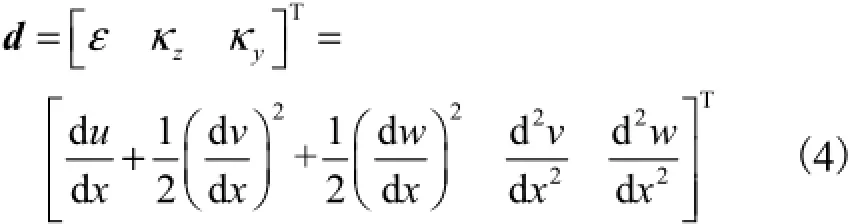
式中：ε为截面轴向应变；κz、κy为绕z、y轴的曲率．

单元内力采用常轴力和线性弯矩并考虑二阶效应，单元截面内力向量q可表示为

式中：N(x)为截面轴力；Mz(x)、My(x)为绕z、y轴的截面弯矩；Nq为单元内力形函数矩阵．

式中L为单元长度．

1.2 截面平衡方程

基于纤维截面广义截面内力与变形关系由截面变形向量dq积分得到截面内力向量qsum，与由节点力向量Q插值得到的截面内力向量q应满足截面平衡方程

式中Dq为截面不平衡力．

1.3 单元刚度矩阵

基于虚位移原理，混合单元平衡方程的虚功方程可表示为

式中：δdTq为截面内力向量q所做的虚功；-δUTP为外荷载向量P所做的虚功．

基于纤维截面广义截面内力与变形关系由截面内力向量q得到单元截面应变向量dq，与由单元截面位移向量u得到的截面应变向量d应满足变形协调性，即

基于Hellinger-Reissner变分[10]，式(8)和式(9)可表示为

经分部积分得到

式中E、C分别为单元求解过程中的不平衡力和残余变形向量．

利用泰勒级数展开式可将非线性方程(12)～(13)线性化，具体过程在文献[9]中已有介绍，这里不再详述．

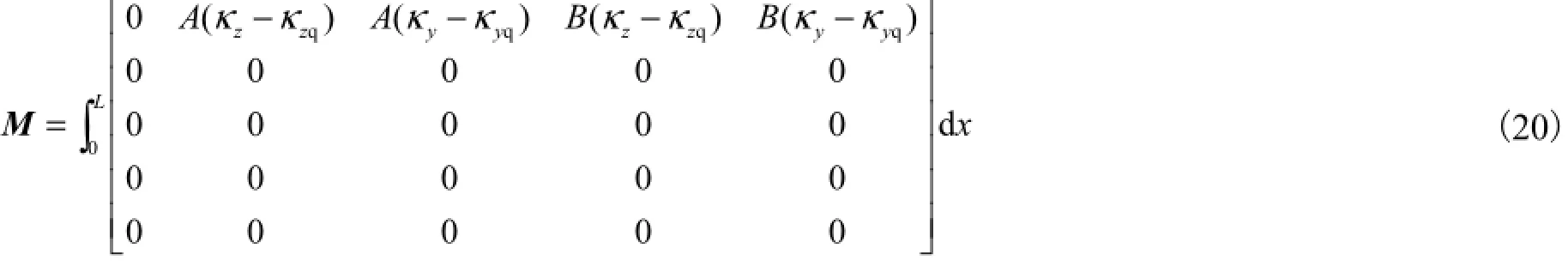
式中：ΔQ为单元节点力增量；ΔU为单元节点位移增量；ΔP为单元外力增量；N为单元轴力．

OpenSees是基于刚度法编制的有限元程序，为了实现将混合单元嵌入该程序，由式(14)、式(15)通过静力凝聚将单元节点力未知量ΔQ消除得到

式中：Ke为混合单元刚度矩阵；Qe为单元内力向量．

1.4 单元状态确定

混合单元需要对截面平衡方程、单元协调方程及单元平衡方程进行求解，单元状态确定过程较为复杂，文献[11]介绍了4种用于混合单元状态确定的算法．Denavit等[9]采用线性算法通过线性求解将截面层次和单元层次的残余误差转化为不平衡力在结构层次进行迭代求解．该算法需要在结构层次进行多次迭代以消除截面不平衡力和单元残余变形的累积误差，需要程序储存大量单元矩阵．由于只在结构层次进行迭代求解，当单元层次残余误差过大时可能导致计算不收敛．

非线性迭代算法在结构层次每一次迭代过程中都会分别在截面层次和单元层次通过迭代将对应的残余误差消除，从而减少结构层次的迭代次数，程序只需储存少量的单元矩阵．本文基于OpenSees采用C++语言编制程序将非线性迭代算法用于混合单元状态确定，具体计算过程如图2所示．

图2 非线性迭代算法Fig.2 Nonlinear iteration algorithm

2 算例分析

2.1 材料本构关系

本文圆钢管混凝土应力-应变曲线(见图3)采用Denavit等[9]改进的Chang-Mander模型，混凝土应力-应变关系为

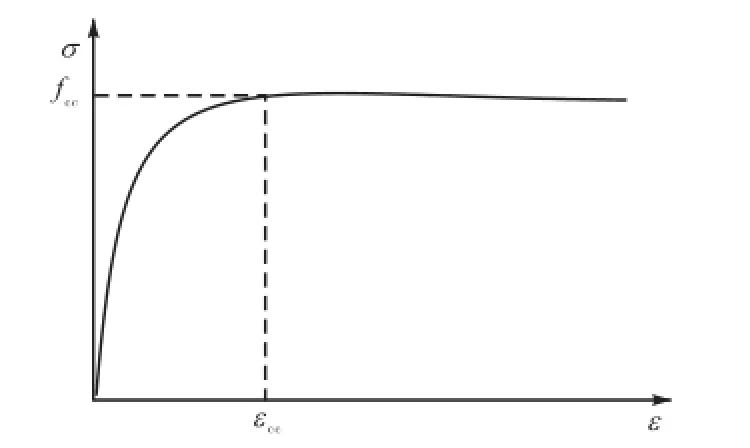
图3 圆钢管混凝土应力-应变曲线Fig.3 Stress-strain relationship curve of circular CFST

本文方钢管混凝土应力-应变曲线(见图4)在混凝土达到峰值应力前参考韩林海[12]模型考虑方钢管对混凝土的约束效应，峰值应力之后参考文献[13]考虑构件截面尺寸、钢管和混凝土强度对混凝土应变软化及残余应力的影响．其应力-应变关系为

图4 方钢管混凝土应力-应变曲线Fig.4 Stress-strain relationship curve of square CFST

核心混凝土峰值应力后应变软化曲线斜率Kc表示为

式中：B/t为方钢管宽厚比；Es为钢材弹性模量．

核心混凝土残余应力frc和对应的压应变εrc可表示为

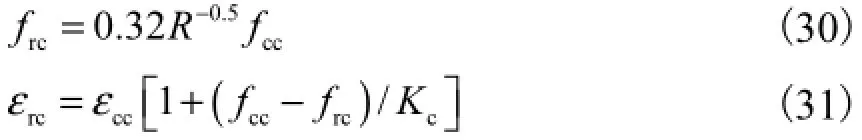
2.2 轴压试验

Han[14]进行了一组细长圆钢管混凝土柱轴压试验，本文选取其中2个试件进行分析，其试验参数见表1，初始缺陷取L/5,000[15]．根据对称性取一半结构采用1个单元模拟，单元设置4个积分点，截面离散为16个钢纤维和32个混凝土纤维．混合单元的计算结果与试验结果对比如图5所示．可见，计算结果与试验结果吻合良好，说明混合单元能较好地反映细长钢管混凝土轴压柱的极限承载力和软化行为．

表1 轴压试验试件参数Tab.1 Test parameters of specimen under axial load

图5 轴压柱混合单元计算结果与试验结果对比Fig.5 Comparison of mixed element computational results and test results of axial compression columns

2.3 偏压试验

Grauers[16]进行了一组方钢管混凝土柱偏压试验，整个加载过程随着荷载的增大试件在轴力和弯矩的共同作用下逐渐表现出材料非线性和几何非线性.本文分别采用混合单元、刚度法单元和柔度法单元对其中7个方钢管混凝土柱进行分析，试件S-2和S-10基本试验参数见表2．

偏压柱3种单元的计算结果与试验结果对比如图6所示．可见，整个加载过程中混合单元计算结果与试验结果吻合良好，较为准确地反映了试件的初始刚度、极限承载力以及软化刚度．基于刚度法单元、柔度法单元的计算结果在加载初期与试验结果吻合较好，随着试件变形增大计算结果与试验结果误差逐渐增大，均高估了试件极限承载能力．

表2 偏压试验试件参数Tab.2 Test parameters of specimen under eccentric load

图6 偏压柱3种单元的计算结果与试验结果对比Fig.6Comparison of computational results and test results of three kinds of elements of eccentric compression columns

表3给出了7个偏压试件的数值计算结果与试验结果误差．从表中可以看出，采用1个混合单元模拟即可得到较为精确的结果；刚度法单元和柔度法单元计算结果与试验结果具有较大误差，需要成倍增加单元数量才能减小计算结果与试验结果误差，严重降低了计算效率．

表3 偏压构件数值计算结果与试验结果误差Tab.3 Errors of computational and test results of eccentric compression member

3 参数对构件几何非线性的影响

以上分析说明不考虑几何非线性会过高估计钢管混凝土构件的承载力．本文针对试件S-10分析了参数对构件几何非线性的影响，参数包括长细比λ和荷载偏心比e/B，其中λ＝40～140，e/B＝0.1～0.5．

图7所示为长细比λ＝140、荷载偏心比e/B＝0.1的计算结果对比．可见，随着变形的增大不考虑几何非线性明显高估构件承载能力，达到极限承载力60%左右时不考虑几何非线性对构件承载力约高估10%，达到构件极限承载力时约高估16%．极限承载力之后相对误差随变形增大逐渐减小并趋于稳定．

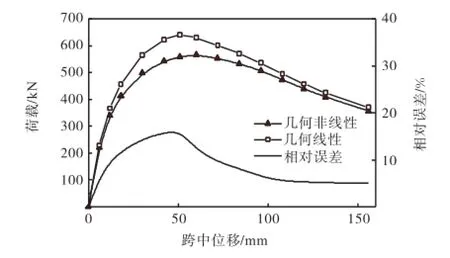
图7 几何非线性参数对构件承载力的影响Fig.7 Influence of geometric nonlinear parameters on bearing capacity of member

图8 所示为构件长细比λ与荷载偏心比e/B对几何非线性的影响．可见，荷载偏心比不变时，相对误差与构件长细比大致呈线性增长关系，且小偏心比情况下相对误差增长更快．构件长细比较小(λ≤80)时，极限承载力相对误差随荷载偏心比变化较为平缓，构件长细比较大(λ＞80)时，极限承载力相对误差随着荷载偏心比增大线性减小，说明大长细比情况下荷载偏心比对几何非线性影响更明显．

图8 长细比与荷载偏心比对几何非线性的影响Fig.8Influence of slenderness ratio and load eccentricity ratio on geometric nonlinearity

4 结 论

(1)建立了一种基于Hellinger-Reissner变分的混合单元，采用非线性迭代算法确定单元状态，并将单元模型嵌入OpenSees用于非线性分析．

(2)采用非线性迭代算法在单元层次和截面层次将残余变形消除，减少了结构层次的迭代次数，具有良好的稳定性．相对于刚度法和柔度法单元，单个构件采用1个混合单元即可较为准确地反映构件强非线性状态下的内力和变形，具有更好的分析精度和计算效率．

(3)不考虑几何非线性对钢管混凝土构件承载力大约高估3%～16%．长细比对几何非线性有明显的影响，长细比越大几何非线性越明显．构件长细比较小(λ≤80)时，荷载偏心比对几何非线性影响较小．构件长细比较大(λ＞80)时，随着荷载偏心比增大，构件几何非线性减弱．

［1］ 聂建国，陶慕轩. 采用纤维梁单元分析钢-混凝土组合结构地震反应的原理[J]. 建筑结构学报，2011，32(10)：1-10.

Nie Jianguo，Tao Muxuan. Theory of seismic response analysis of steel-concrete composite structures using fiber beam elements[J]. Journal of Building Structures，2011，32(10)：1-10(in Chinese).

［2］ 王文达，韩林海. 钢管混凝土框架结构力学性能非线性分析[J]. 建筑结构学报，2008，29(6)：75-86.

Wang Wenda，Han Linhai. Nonlinear finite elementanalysis on mechanical performance of concrete filled steel tubular frame structure[J]. Journal of Building Structures，2008，29(6)：75-86(in Chinese).

［3］ 夏拥军，陆念力. 梁杆结构二阶效应分析的一种新型梁单元[J]. 工程力学，2007，24(7)：39-43.

Xia Yongjun，Lu Nianli. A new beam element for second-order effect analysis of beam structures [J]. Engineering Mechanics，2007，24(7)：39-43(in Chinese).

［4］ 许红胜，周绪红，舒兴平. 空间钢框架几何非线性分析的一种新单元[J]. 工程力学，2003，20(4)：39-44.

Xu Hongsheng，Zhou Xuhong，Shu Xingping. A new element for geometric nonlinear analysis of threedimensional steel frames[J]. Engineering Mechanics，2003，20(4)：39-44(in Chinese).

［5］ 陈 滔，黄宗明. 基于有限单元柔度法的材料与几何双重非线性空间梁柱单元[J]. 计算力学学报，2006，23(5)：524-528.

Chen Tao，Huang Zongming. Material and geometrically nonlinear spatial beam-column elements based on the finite element flexibility method[J]. Journal of Computational Mechanics，2006，23(5)：524-528(in Chinese).

［6］ 陈 滔，黄宗明. 基于有限单元柔度法和刚度法的几何非线性空间梁柱单元比较研究[J]. 工程力学，2005，22(3)：31-38.

Chen Tao，Huang Zongming. Comparison between flexibility-based and stiffness-based geometrically nonlinear beam-column elements[J]. Engineering Mechanics，2005，22(3)：31-38(in Chinese).

［7］ Alemdar B N. Distributed Plasticity Analysis of Steel Building Structural Systems[D]. Atlanta：Department of Civil and Environmental Engineering，Georgia Institute of Technology，2001.

［8］ Tort C，Hajjar J F. Mixed finite element for threedimensional nonlinear dynamic analysis of rectangular concrete-filled steel tube beam-columns[J]. ASCE Journal of Structural Engineering，2010，136：1329-1339.

［9］ Denavit M D，Hajjar J F. Nonlinear seismic analysis of circular concrete-filled steel tube members and frames [J]. Journal of Structural Engineering，138(9)：1089-1098.

［10］ Zienkiewicz O C，Taylor R L. The Finite Element Method for Solid and Structural Mechanics[M]. 6th ed. Butterworth-Heinemann Ltd，Elsevier，2005.

［11］ Nukala P K，White D. Variationally consistent state determination algorithms for nonlinear mixed beam finite elements[J]. Computer Methods in Applied Mechanics Engineering，2004，193：3647-3666.

［12］ 韩林海. 钢管混凝土结构：理论与实践[M]. 2版. 北京：科学出版社，2007.

Han Linhai. Concrete Filled Steel Tubular Structures：Theory and Practice[M]. 2nd ed. Beijing：Science Press，2007(in Chinese).

［13］ Tort C，Hajjar J F. Mixed finite element approach for performance-based design of rectangular concrete-filled steel tube frames[C]//Composite Construction in Steel and Concrete Composite，Ⅵ-Proceedings of the 2008 Composite Construction in Steel and Concrete Conference. Tabemash，CO，USA，2011：591-603.

［14］ Han Linhai. Test on concrete filled steel tubular columns with high slenderness ratio[J]. Advances in Structural Engineering，2000，3(4)：337-344.

［15］ An Yufeng，Han Linhai，Zhao Xiaoling. Behavior and design calculations on very slender thin-walled CFST columns[J]. Thin-Walled Structures，2012，53：161-175.

［16］ Grauers M. Composite Columns with Hollow Steel Section Filled with High Strength Concrete [D]. Goteborg：Department of Structural Engineering and Mechanics，Chalmers University of Technology，1993.

(责任编辑：樊素英)

Development and Application of Mixed Element Based on Hellinger-Reissner Variation

Ding Yang1,2，Lai Chenggang1，Li Ning1,2，Li Zhongxian1,2
(1. School of Civil Engineering，Tianjin University，Tianjin 300072，China；2. Key Laboratory of Coast Civil Structure Safety of Ministry of Education，Tianjin University，Tianjin 300072，China)

This paper proposed a beam-column mixed element based on Hellinger-Reissner variation for geometric and material nonlinear analysis. A governing differential formulation of mixed element is established using displacement shape function and force shape function including second-order effects for interpolation of section deformation and innerforce，respectively．The element stiffness matrix and internal forces are derived by eliminating the force unknown through static condensation. During the element state determination，nonlinear iteration algorithm is adopted for residual error of section equilibrium and element compatibility，which reduces the numerical cost of structural equilibrium iteration. This mixed element based fiber section is used for numerical studies of concrete filled steel tube(CFST) members，and the results indicate good agreement. Relative to the displacement-based and flexibility-based elements，the mixed element based Hellinger-Reissner variation was more reasonable in predicting geometric and material nonlinearity of members，and the nonlinear iteration algorithm carried out for element state determination is of good efficiency and stability. Finally，a parametric study for geometric nonlinearity of CFST was performed based on the mixed element model.

Hellinger-Reissner variation；mixed element；nonlinear iteration；geometric nonlinearity；material nonlinearity；concrete filled steel tube(CFST)

O344.3

A

0493-2137(2015)05-0422-07

10.11784/tdxbz201310064

2013-10-25；

2013-11-20.

国家重点基础研究发展计划(973计划)资助项目(2011CB013606，2011CB013603)；国家自然科学基金紫霞湖项目(51238007，

51378341，51178306)；天津市自然科学基金资助项目(13JCZDJC35200，13JCQNJC07200).

丁 阳（1966— ），女，博士，教授.

李 宁，neallee@tju.edu.cn.

时间：2013-12-31. 网络出版地址：http://www.cnki.net/kcms/doi/10.11784/tdxbz201310064.html.