雷诺质流模型在填料床反应过程中的应用:Ⅰ. MEA吸收CO2过程的模拟
2015-06-05李文彬刘伯潭余国琮袁希钢
李文彬,刘伯潭,余国琮,袁希钢
雷诺质流模型在填料床反应过程中的应用:Ⅰ. MEA吸收CO2过程的模拟
李文彬,刘伯潭,余国琮,袁希钢
(天津大学化学工程研究所,天津300072)
工业中填料床往往处于湍流操作条件下,导致传质扩散呈现各向异性.针对填料床反应过程的预测,本文采用了雷诺质流模型,该模型的特点是通过直接求解雷诺质流方程来封闭湍流传质方程,从而准确表征填料床内湍流传质扩散的各向异性,得到更为准确的组分浓度、流体温度及速度分布.本文模拟了散堆填料塔内一乙醇胺溶液(MEA)-CO2化学吸收过程.模拟结果与文献报道的实验数据符合较好,验证了模型的可靠性.
填料床;吸收;模拟;各相异性湍流扩散;计算传质学
填料床是化学工业生产中最为常用的一种装置,例如工业上常用于精馏、萃取、反应以及吸附等单元操作.
随着工业上对填料床性能的要求越来越高,填料床的优化及放大成为许多研究者关心的问题.要对填料床进行合理优化或者放大,研究者通常需要先做大量的小试实验以确定填料床内流体的速度、组分浓度以及温度分布的信息,了解相关参数对填料床性能的影响规律,并在此基础上根据经验系数来逐级放大其规模.通常这样的实验成本很高,也费时费力.因此,近些年数值模拟越来越受到大家的关注.随着计算机技术以及相关计算软件的飞速发展,计算流体力学已经成为一种可靠的计算机实验方法.通过计算流体力学(CFD)模拟,研究者可以得到填料床局部的速度、浓度以及温度分布信息.这对填料床的优化和放大都是至关重要的.目前,用于模拟填料床的CFD模型可以分为两大类.第1类是“填料算法”(packing algorithm)[1].这类模型的特点是应用特定的数学方法[2-3]直接计算填料床层中的流体流动.其优点是模拟得到的填料床层中流体流动更接近真实过程.但是模拟过程中需要消耗巨大的计算资源.到目前为止,采用这类方法模拟的填料床层,其填料颗粒的总数至多1,250个[4].显然,相比于工业应用的填料床,这一数量是很少的.第2类是“水力学类比法”(hydrodynamic analogy method)[5].这类方法的特点是将填料床层处理为一种多孔介质,同时将其径向空隙率分布考虑在内[6-11].这样做的优点就是把复杂的填料颗粒排列简化为一种简单地相含率分布模式,从而大大节省所需的计算资源.
以上介绍了填料床内流体力学模拟的方法.而对填料床反应性能(或传质性能)的考察,则需要借助计算传质学模拟.传统的计算传质学模型需要估算湍流传质扩散系数来模拟组分浓度场.而湍流传质扩散系数的估算又往往借助于经验关联式或经验施密特数/皮克列数.Liu等[12]则采用严格的双方程模型来估算湍流扩散系数.该模型相比于之前的经验模型能更准确地预测湍流扩散系数,但模型中该系数的求解仍然采用了各向同性的假设.即认为沿填料床轴向、径向的湍流扩散系数相等.然而,已有大量实验证明[13-15],填料床中的湍流扩散具有各向异性的特征.因此,很多研究者都认为在填料床的模拟中应当考虑湍流扩散的各向异性[13-18],从而获得更为准确的模拟结果.
实际上,有很多研究人员都尝试通过实验方法来关联各向异性的湍流扩散系数[13-15].但是,不同实验关联式得到的各向异性湍流扩散系数在数值上差异较大.这主要是由于他们在确定湍流扩散系数时所采用的实验方法和计算模型不同导致的.可见,采用这类实验关联式,尽管能在一定程度上表征出湍流扩散的各向异性.但是可以想象,采用不同的实验关联式将得到不同的浓度场.这就给模拟带来很大的不确定性.为了降低这种不确定性,Li等[19]提出了“雷诺质流模型”来模拟精馏塔内的组分浓度分布.雷诺质流模型的特点是通过加入辅助模型方程,以准确预测各向异性的湍流扩散系数,从而摆脱对经验关联式的依赖.
笔者的研究目的在于建立适用于填料床反应过程模拟的雷诺质流模型.论文首先描述了雷诺质流模型的基本构成.然后,为了验证模型的可靠性,对一乙醇胺溶液(MEA)-CO2化学吸收过程进行了模拟,模拟结果对比了文献报道的实验数据.
1 模型方程
雷诺质流模型由以下3部分组成:①湍流传质方程以及用于封闭该方程的雷诺质流方程;②计算流体力学(CFD)方程组;③计算传热学(CHT)方程组.
1.1 湍流传质方程及其封闭方程
流体中某组分的湍流传质方程为
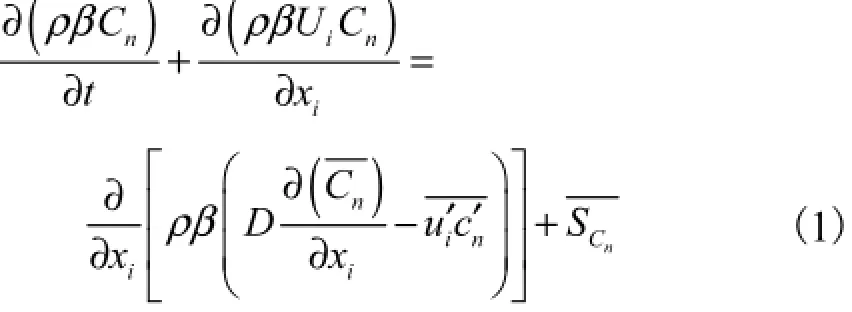
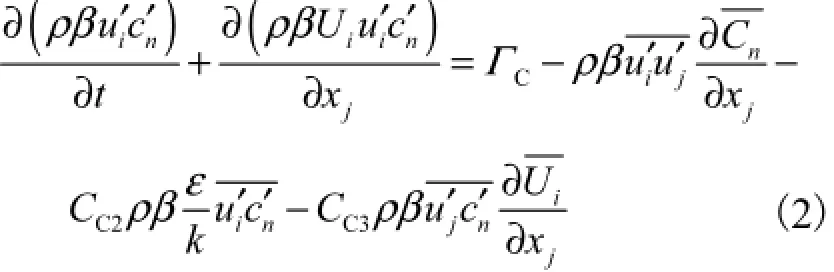
式中CΓ表示雷诺质流方程的扩散项,由下式确定:
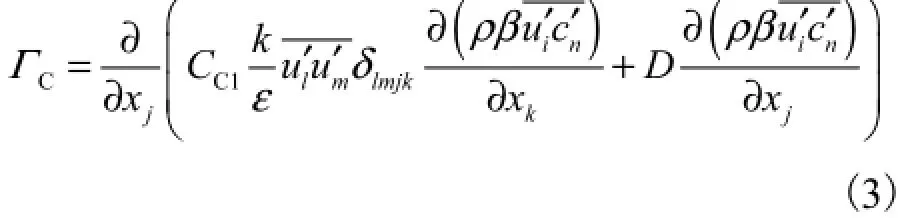
模型参数分别为[
1.2 计算流体力学方程组
计算流体力学(CFD)模型方程组是由描述流体流动的连续性方程、湍流动量传递方程以及封闭湍流动量传递方程的雷诺应力方程共同构成.
连续性方程
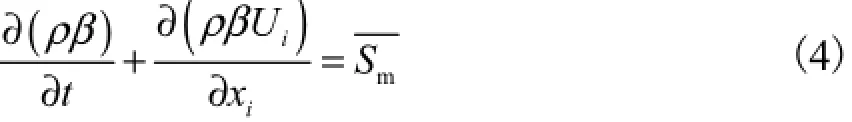
湍流动量传递方程
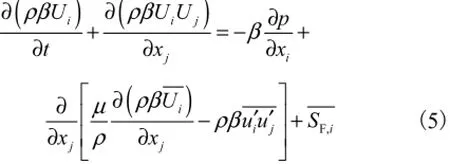
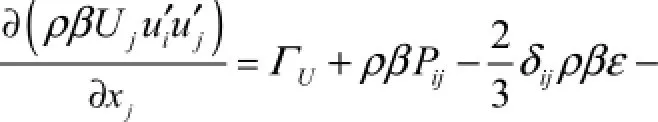
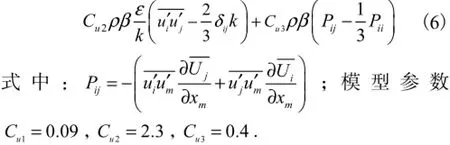
方程(6)中的UΓ为雷诺应力方程的扩散项,由下式确定:
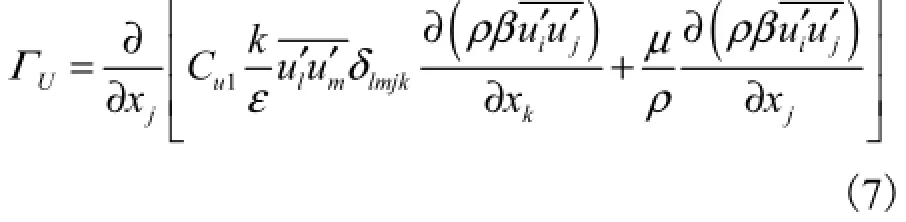
其中湍动能k以及湍动能耗散率ε则由以下方程求解:
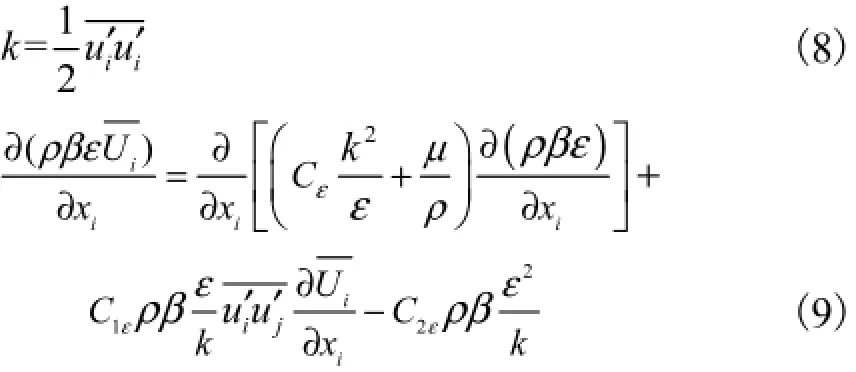
需要说明的是,本文虽然采用了湍动能k方程以及湍动能耗散率ε方程来辅助求解雷诺应力,但并非采用了k-ε湍流模型来求解速度场.
1.3 计算传热学方程组
计算传热学方程组包括流体湍流传热方程以及封闭该方程的雷诺热流方程.流体湍流传热方程:
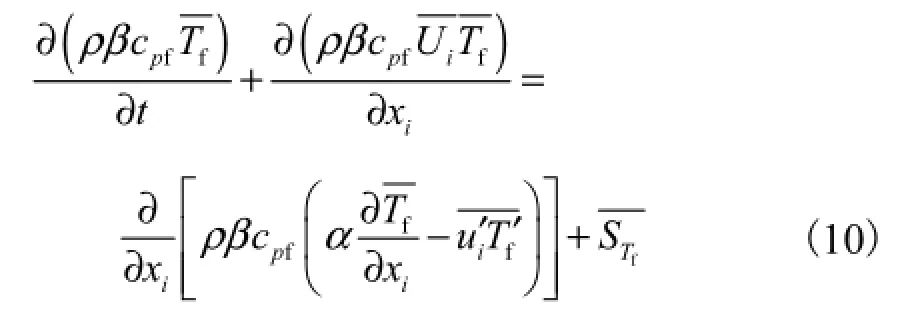
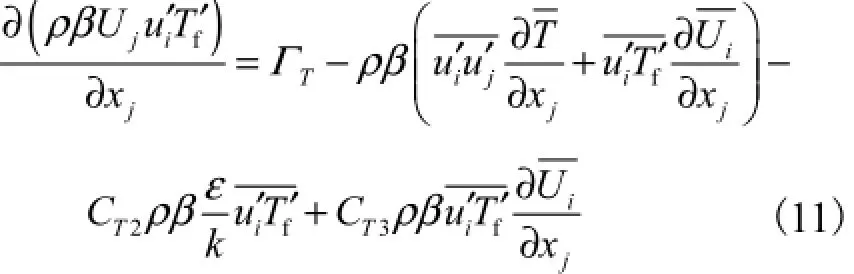
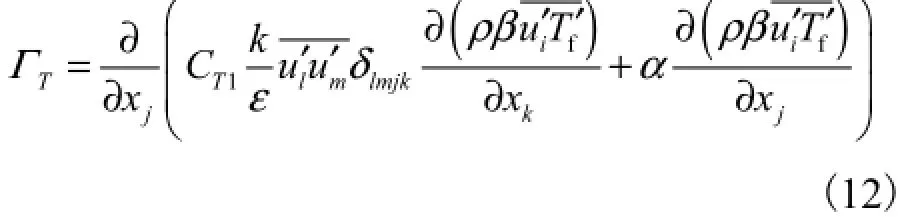
式中模型参数CT1=0.07.
2 模型实施
本节阐述如何将雷诺质流模型应用于填料床MEA水溶液化学吸收CO2过程的模拟,主要包括化学反应机理、模型方程中一些未知项的确定方法、模型边界条件设置以及数值计算步骤等.
此外,为了采用雷诺质流模型来描述填料床内化学吸收过程的流体流动、传热、传质等过程,本文提出以下假设:
(1) 化学吸收过程为稳态,液相不可压缩,填料吸收塔为二维轴对称;
(2) 气相中只有CO2会被液相吸收,而液相中作为溶质的水不会向气相挥发;
(3) CO2被水溶液吸收时放出的溶解热以及与MEA反应时放出的反应热都将被液相迅速吸收,同时忽略液相与气相、液相与固相之间的热量传递;
(4) 吸收过程处于绝热操作条件下,即忽略吸收塔与环境的热交换.
2.1 MEA水溶液与CO2的反应机理
Astarita等[21]以及Danckwerts[22]研究了MEA水溶液与CO2的反应机理,认为CO2被液相吸收并与液相中碳化率小于0.5的MEA发生反应的过程,一般分为以下几个步骤进行:
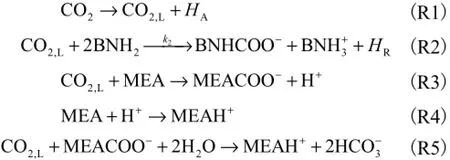
Babak等[23]指出,反应(R2)可认为是整个反应的控制过程,并认为当MEA碳化率不超过0.5时,这一控制步骤为一不可逆二级反应.因此,可以认为MEA水溶液吸收CO2是一个伴有不可逆二级化学反应的过程.总反应速率由下式确定[24]:

2.2 模型方程中未知项的确定
连续性方程源项表示填料塔内液相吸收CO2导致的质量变化,可根据双膜理论计算,即
式中:KOG为基于气相的总包传质系数;2COM为二氧化碳的分子质量;pCO2为气相中CO2分压;表示与液相平衡的CO2分压.
基于气相的总包传质系数为

式中:kL、kG分别为液相、气相膜传质系数;E为因伴随化学反应而导致的传质增强因子,可由Danckwerts[25]提出的关联式确定;H为亨利常数,由Mandal等[26]提出的方法确定.
对于液相、气相膜传质系数kL、kG可采用Onda等[27]提出的关联式来计算,即
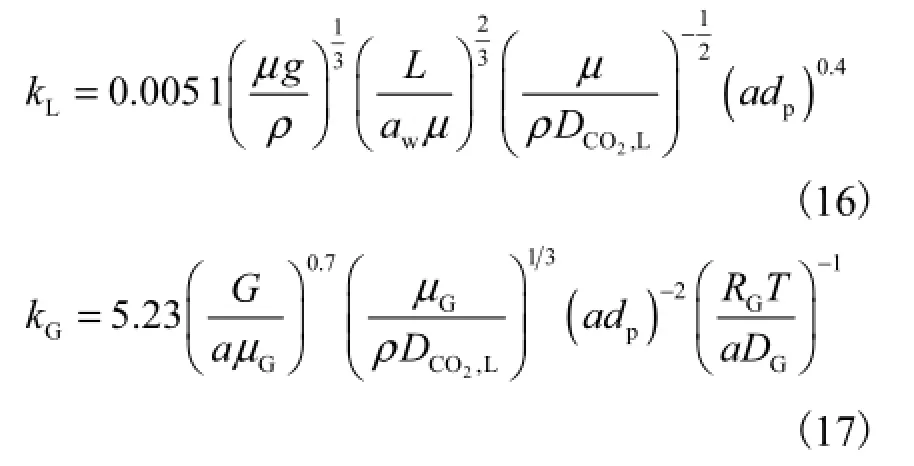
其中填料的有效传质界面面积ae可认为等于润湿比表面积aw,并由Onda等[27]提出的关联式确定.L为局部液相流率,可表示为

MEA水溶液的分子黏度µ由Weiland等[28]提出的关联式来计算.气相分子黏度由Perry等[29]报道的关联式确定.CO2在气相中的分子扩散系数DG根据Poling等[30]提供的方法计算.而CO2在MEA水溶液中的分子扩散系数DCO2,L则通过校正N2O在MEA水溶液中的分子扩散系数得到[26].此外,方程(1)中MEA在MEA水溶液中的分子扩散系数D由下式确定[31]:
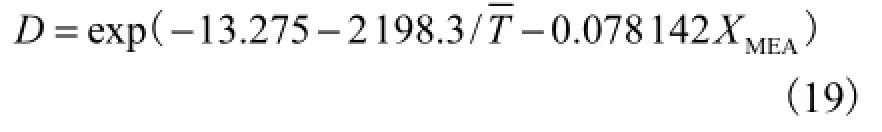
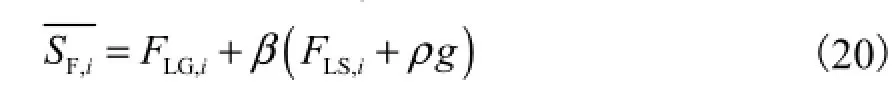
式中:LG,iF表示气液相间曳力;LS,iF为填料对流体流动造成的阻力.气液相间曳力由以下方法确定:

式中tpΔ气相通过填料塔时的压降,可以认为tpΔ是由干填料压降与因气液相间作用而导致的压降的加和. 而干填料压降和气液相间作用力导致的压降可通过Robbins[32]提出的方法计算;slipU为气液相对速度.slipU由下式确定:

而固体填料对液体流动造成的阻力LS,iF可以根据Ergun[33]提出的经验关联式计算.液相含率β则根据下式确定:

式中:γ表示散堆填料床的局部空隙率,可由Liu[34]提出的关联式计算;ht为填料床总持液量,可根据下式确定:

式中:hs为填料床静持液量,可根据Engel等[35]提出的关联式计算;oph为动持液量,可通过Sater等[36]提出的方法计算.
以MEA水溶液中MEA作为关键组分,湍流传质方程(1)中源项表示单位体积内因吸收气相中CO2并发生化学反应而消耗MEA的速率.根据反应(R2),可得

根据反应步骤(R1)以及(R2),可得到液相传热方程源项为

式中:CO2溶解热反应热
2.3 模型边界条件的确定
液体以一定的初始速度、温度、浓度分布由塔顶自上而下流过填料床层,在填料塔吸收气相中的CO2,最后从塔底流出.边界条件如图1所示,具体设置如下.
1) 入口条件
速度、温度和质量浓度的入口条件根据实验条件来确定:
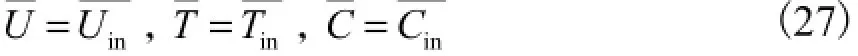
对于雷诺质流以及雷诺热流方程的入口条件设置由下式确定:
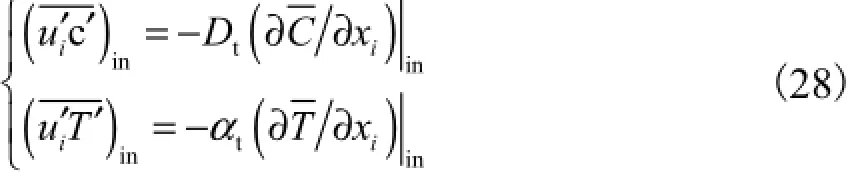
而入口处的湍流传质扩散系数Dt与湍流传热扩散系数αt则分别采用湍流施密特数(Sct)和湍流普朗特数(Prt)模型近似估算.Sct一般都设置在0.6~1.0,本文将其设置为在工程上常用的Sct=0.7,而Prt则设置为Prt=0.9.
2) 出口条件
填料床出口处认为湍流充分发展,即在主流方向除压力外所有物理量的梯度为零.
3) 轴对称条件
由于填料床为柱形,因此在模拟填料塔内的化工过程时,可以将计算域按二维轴对称模型进行简化.在对称轴上,所有变量的径向梯度都为零.
4) 壁面条件
对填料塔模拟采用壁面无滑移条件,除热通量外其余所有变量在壁面处的通量都为零.
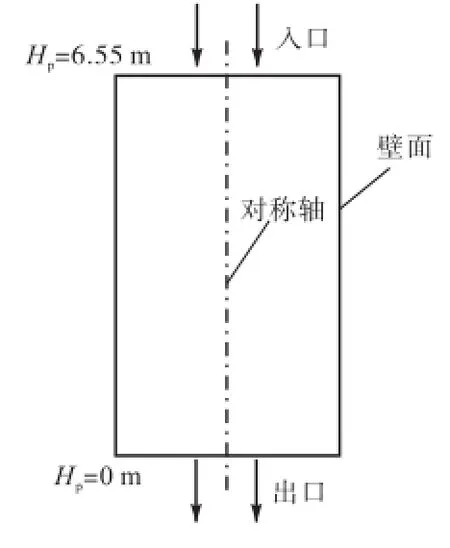
图1 边界条件的设置Fig.1 Setting of boundary conditions
2.4 数值模拟
本文模拟的是1992年Tontiwachwuthikul等[38]报道的散堆填料床MEA水溶液化学吸收CO2的实验.塔高为6.55,m、内径为0.1,m的填料塔内装有直径为12.7,mm的鲍尔环填料.操作压力为760,kPa.吸收塔内向下流动的液相为一乙醇胺水溶液,用来吸收向上流动气体中的CO2.
采用Fluent 6.3.26的二维轴对称稳态求解器,速度压力耦合问题采用SIMPLEC算法,对填料高度为6.55,m、直径为0.1,m的填料塔共划分了160,000个四边形网格,其中轴向上布置2,000个网络,径向上布置80个网络,在近壁区采用加密网格.残差收敛判断标准控制在1.0×10-6以下,以保证计算的精度.
对于数值计算,网格划分精度对计算结果有很大影响,为了得到网格独立解,往往需要精度很高的网格.为了考察网格精度对模拟结果的影响,本文还采用了更高精度的网格,而在计算域轴向上布置2,000个网络,径向上布置160个网络.两种网格精度下的模拟结果如图2所示,可见差别非常小,说明本文的网格精度(2,000×80)已足够.
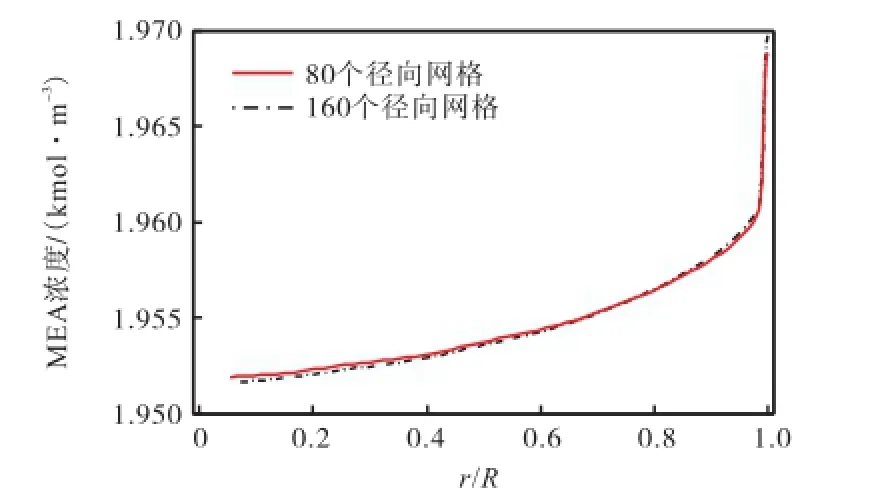
图2 网格精度对计算结果的影响Fig.2 Effect of grid resolution on simulation results
3 模拟结果与讨论
Tontiwachwuthikul等[38]报道了10组实验数据(T13~T22),本文仅以实验T17为例与模拟结果进行对比,其主要操作条件见表1.
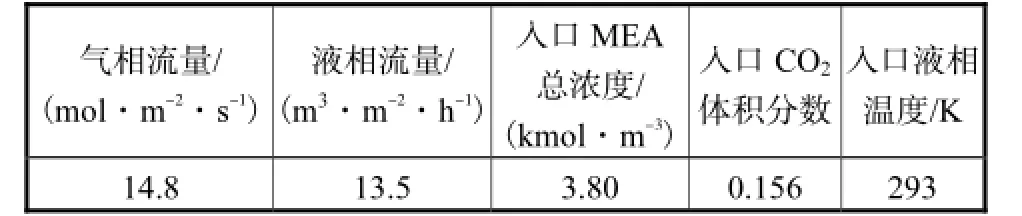
表1 实验T17的主要操作条件Tab.1 Main operating conditions for experiment T17
3.1 液相MEA碳化率分布
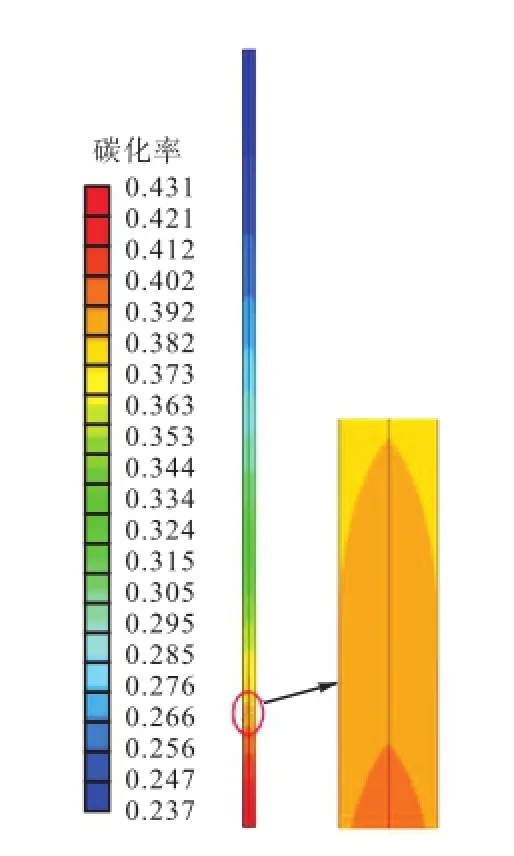
图3 液相MEA碳化率在填料床内的分布Fig.3 Profile of CO2loading in the packed bed
图3和图4分别给出了填料床内液相MEA碳化率的全塔云图以及轴向分布.从图3可以看出,CO2的化学吸收主要发生在填料床的下段(靠近液相出口,也即气相的入口端),而填料床上段只吸收很少的CO2.模拟得到的液相MEA碳化率轴向分布与实验测量对比见图4.从图4可以看出模拟得到的MEA碳化率与实验测量值符合较好.
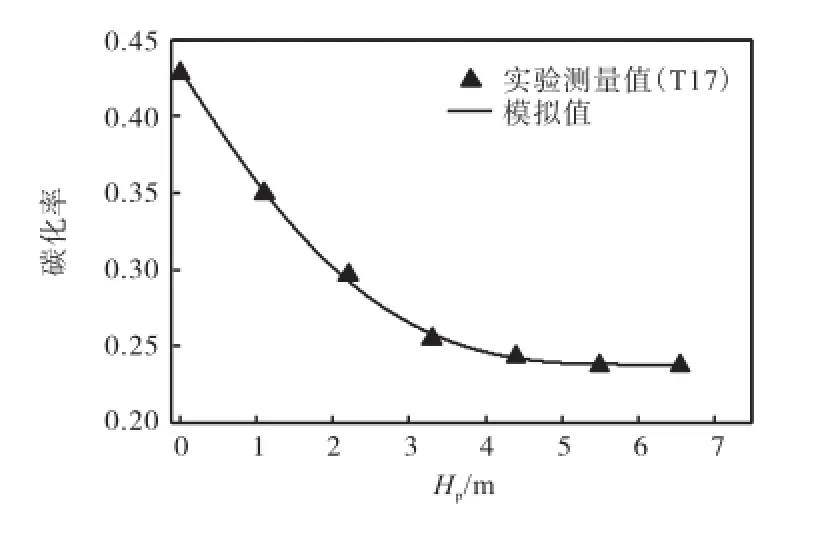
图4 液相MEA碳化率在填料床内的轴向分布Fig.4 Axial distributions of CO2loading in the packed bed
3.2 液相自由MEA分布
从图5可以看出,在同一填料高度上,液相中自由MEA的摩尔浓度沿塔中心到塔壁逐渐增大.这是由于散堆填料塔近壁区的液相速度减小,从而导致液相与气相的接触变差,气相中只有较少的CO2被液相吸收,因此液相中自由MEA的浓度就比塔中心区域高.这同样解释了图3中,在同一填料高度上,液相MEA碳化率沿塔中心向塔壁逐渐减小的趋势.
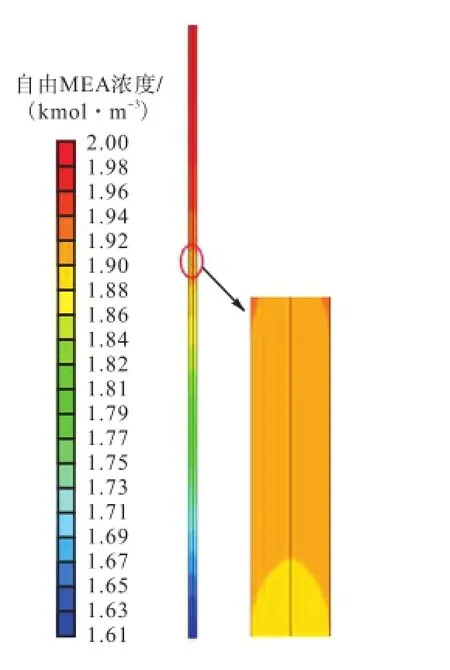
图5 液相自由MEA在填料床内的分布Fig.5 Profile of free MEA in the packed bed
3.3 液相温度分布
图6给出了填料床内液相温度分布.从图中可以看出,在同一填料高度上,液相温度在靠近壁面处下降.如第3.2节中的分析,这是因为在靠近壁面区域液相MEA与CO2反应减少,反应放热也随之减少,故液相温度低.
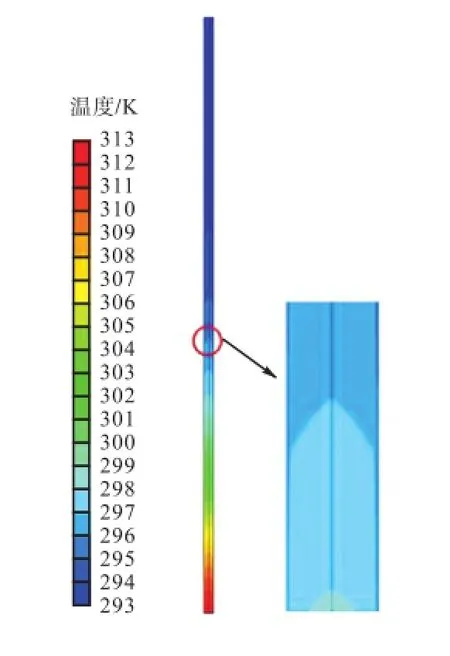
图6 填料床内液相温度的分布Fig.6 Profile of liquid temperature in the packed bed
图7为模拟的液相温度与实验测量值对比.模拟的液相温度比实验测量值稍大.这一偏差的出现是由于模型假设了填料床壁面绝温,即忽略了壁面向环境的热损失,从而模拟的液相温度高于实验测量值.
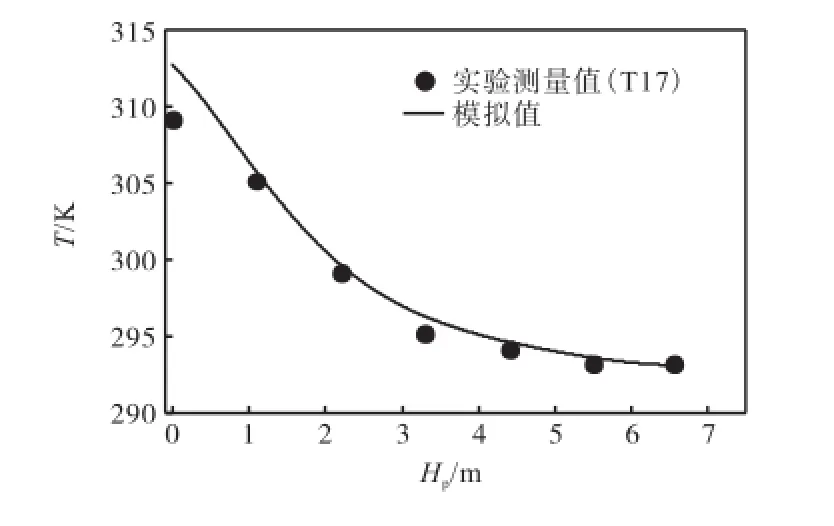
图7 填料床内液相温度的轴向分布Fig.7Axial distribution of liquid temperature in the packed bed
3.4 液相速度分布
不同填料高度上液相速度的分布情况基本一致,因此图8只给出填料高度Hp=2.2,m处液相速度的径向分布.从图8可以看出,靠近壁面处(r/R从0.8到1.0)出现明显的波动,这是这一区域填料空隙率分布不均匀所致.而r/R从0到0.8时,轴向速度基本保持恒定.这一结果与很多研究者的实验观察相吻合[34,39].
3.5 各向异性的湍流传质扩散系数分布
采用标准雷诺质流模型能直接求得各向异性的雷诺质流.图9(a)和9(b)分别给出了轴向、径向雷诺质流分布.
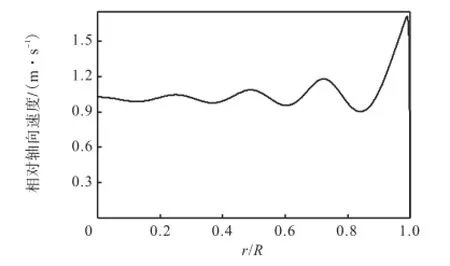
图8 填料高度为2.2 m处液相速度的径向分布Fig.8 Radial distribution of liquid velocity at Hp=2.2 m
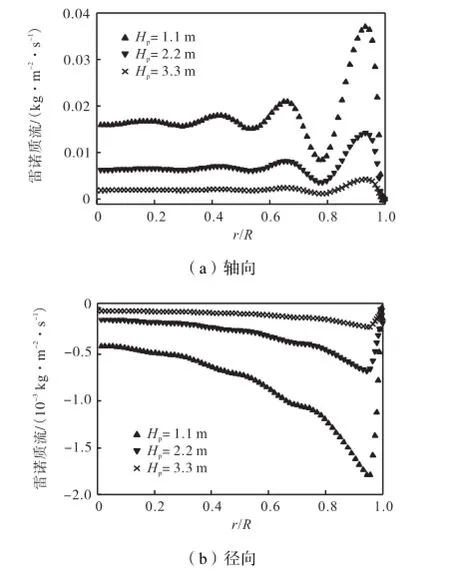
图9 填料床内各向雷诺质流分布Fig.9 Distributions of Reynolds mass flux in different directions in the packed bed
此外,依据经典Boussinesq假设,还可以反算各向异性的湍流传质扩散系数,即
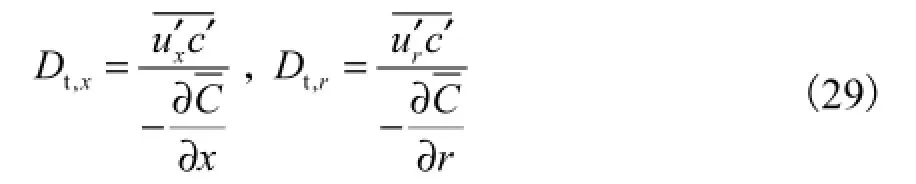
式中:Dt,x、Dt,r分别为轴向、径向湍流传质扩散系数;分别为轴向、径向雷诺质流;∂C∂x、分别为浓度轴向、径向梯度,见图10(a)、(b).
传统模型使用的湍流传质扩散系数一般通过示踪剂实验或经验关联式计算得到,而且湍流传质扩散系数往往只与轴向的组分浓度梯度相关且为标量.而本文反算得到的湍流传质扩散系数不仅与轴向组分浓度梯度有关,还与径向组分浓度梯度有关,表现出各向异性(见图11).
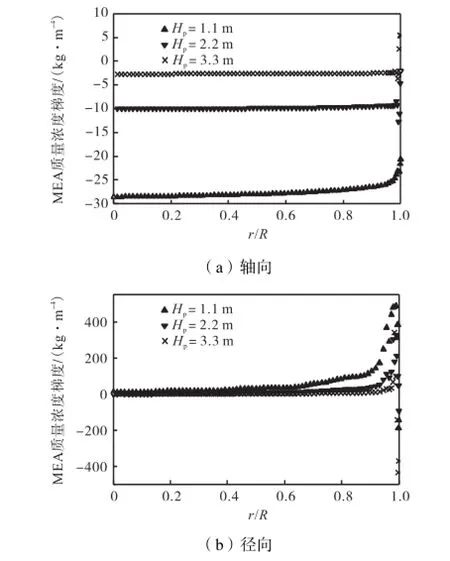
图10 自由MEA浓度梯度分布Fig.10Distributions of free MEA concentration gradient
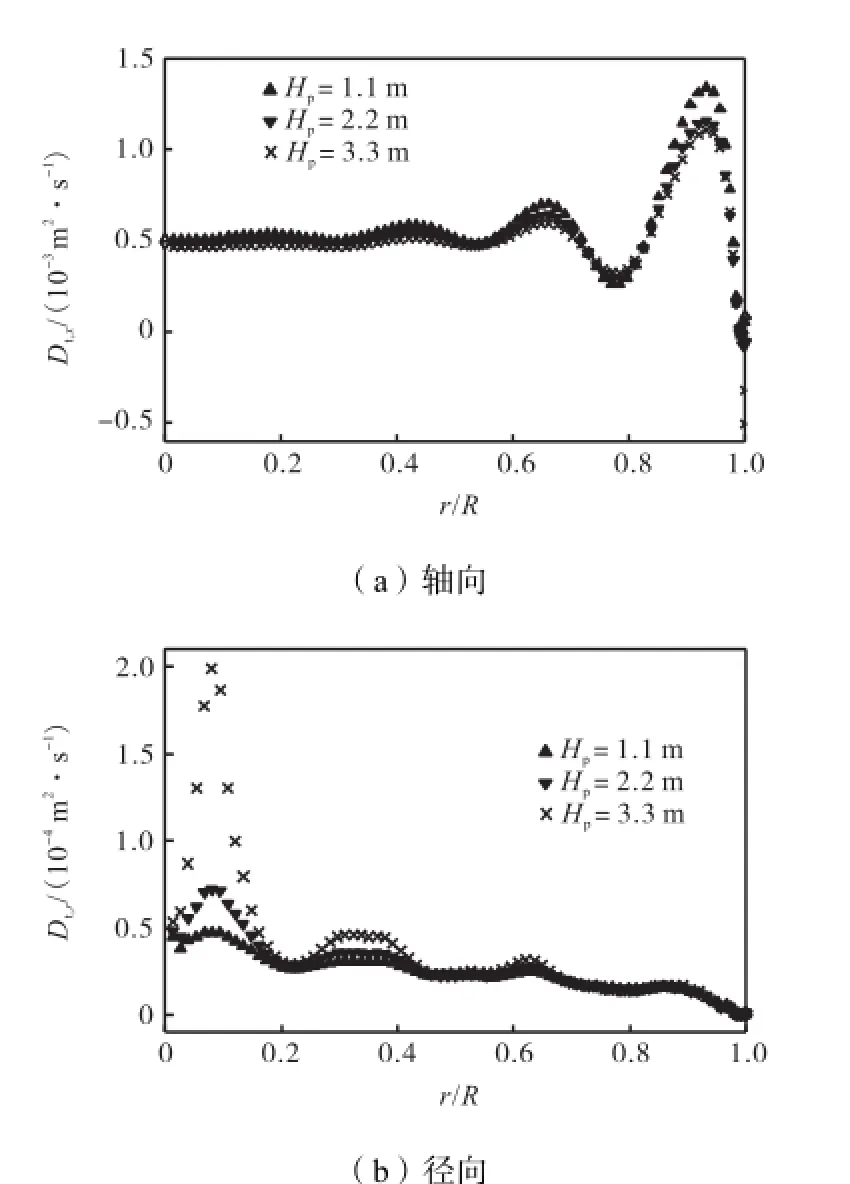
图11 填料床内各向湍流传质扩散系数分布Fig.11Distributions of anisotropic turbulent mass diffusivity in the packed bed
从图11(a)中可以看出在同一填料高度上,轴向湍流传质扩散系数Dt,x在填料床中心区域基本为一定值,而在近壁区则迅速减小,这和图9(a)中轴向雷诺质流分布的趋势是基本一致的.图11(b)中各个填料高度上的径向湍流扩散传质系数都在塔中心附近有一突变,即沿r/R=0.2至r/R=0径向雷诺质流增大了近7倍.这主要是因为模型假设填料床为二维轴对称柱体,因此在填料床轴线上即r/R=0处浓度径向梯度从而使得该区域出现较大的径向湍流传质扩散系数.
4 结 语
本文应用雷诺质流模型对填料床反应过程进行了模拟.采用该模型可以同时得到填料床内流体速度场、温度场以及组分浓度场.雷诺质流模型的特点是通过直接求解雷诺质流封闭湍流传质方程,从而能够准确表征填料床反应过程中的湍流传质扩散.本文模拟对象为填料床MEA水溶液化学吸收CO2过程,模拟结果与实验对比符合较好,从而证明本文的雷诺质流模型适用于填料床反应过程模拟.
[1] Jia X,Williams R A. A packing algorithm for particles of arbitrary shapes[J]. Powder Technology,2001,120(3):175-186.
[2] Nijemeisland M,Dixon A G. CFD study of fluid flow and wall heat transfer in a fixed bed of spheres[J]. AIChE Journal,2004,50(5):906-921.
[3] Dixon A G,Nijemeisland M,Stitt E H. Packed tubular reactor modeling and catalyst design using computational fluid dynamics[C]// Advances in Chemical Engineering. New York:Academic Press,2006:307-389.
[4] Dixon A G,Walls G,Stanness H,et al. Experimental validation of high Reynolds number CFD simulations of heat transfer in a pilot-scale fixed bed tube[J]. Chemical Engineering Journal,2012,200/201/202:344-356.
[5] Kenig E Y. Multicomponent multiphase film-like systems:A modelling approach[J]. Computers and Chemical Engineering,1997,21(Suppl):355-360.
[6] Daszkowski T,Eigenberger G. A reevaluation of fluid flow,heat transfer and chemical reaction in catalyst filled tubes[J]. Chemical Engineering Science,1992,47(9/10/11):2245-2250.
[7] Papageorgiou J N,Froment G F. Simulation models accounting for radial voidage profiles in fixed-bed reactors[J]. Chemical Engineering Science,1995,50(19):3043-3056.
[8] Legawiec B,Zió/klkowski D. Mathematical simulation of heat transfer within tubular flow apparatus with packed bed by a model considering system inhomogeneity[J]. Chemical Engineering Science,1995,50(4):673-683.
[9] Jakobsen H A,Lindborg H,Handeland V. A numerical study of the interactions between viscous flow,transport and kinetics in fixed bed reactors[J]. Computers and Chemical Engineering,2002,26(3):333-357.
[10] Koning G W. Heat and Mass Transport in Tubular Packed Bed Reactors at Reacting and Non-Reacting Conditions:Experiments and Models[D]. Enschede,The Netherlands:University of Twente,2002.
[11] Castillo-Araiza C O,López-Isunza F. Modeling the partial oxidation of o-xylene in an industrial packed-bed catalytic reactor:The role of hydrodynamics and catalyst activity in the heat transport[J]. Industrial & Engineering Chemistry Research,2010,49(15):6845-6853.
[12] Liu G B,Yu K T,Yuan X G,et al. A computational transport model for wall-cooled catalytic reactor[J]. Industrial & Engineering Chemistry Research,2008,47(8):2656-2665.
[13] Delgado J M P Q. A critical review of dispersion in packed beds[J]. Heat Mass Transfer,2006,42(4):279-310.
[14] Koplik J,Redner S,Wilkinson D. Transport and dispersion in random networks with percolation disorder [J]. Physical Review A,1988,37(7):2619-2636.
[15] Sahimi M. Flow and Transport in Porous Media and Fractured Rock[M]. Weinheim,Germany:VCH Velagsgesellschaft mbH,1995.
[16] Yin F H,Sun C G,Afacan A,et al. CFD modeling of mass-transfer processes in randomly packed distillation columns[J]. Industrial & Engineering Chemistry Research,2000,39(5):1369-1380.
[17] Foumeny E A,Chowdhury M A,McGreavy C,et al. Estimation of dispersion coefficients in packed beds[J]. Chemical Engineering & Technology,1992,15(3):168-181.
[18] Adnani P,Catton I,Abdou M A. Non-darcian forced convection in porous media with anisotropic dispersion [J]. Journal of Heat Transfer,1995,117(2):447-451.
[19] Li W,Liu B,Yu G,et al. A new model for the simulation of distillation column[J]. Chinese Journal of Chemical Engineering,2011,19(5):717-725.
[20] Chen C J,Jaw S J. Fundamentals of Turbulence Modeling[M]. Washington:Taylor & Francis,1998.
[21] Astarita G,Marrucci G,Gioia F. The influence of carbonation ratio and total amine concentration on carbon dioxide absorption in aqueous monoethanolamine solutions[J]. Chemical Engineering Science,1964,19(2):95-103.
[22] Danckwerts P V. The reaction of CO2with ethanolamines[J]. Chemical Engineering Science,1979,34(4):443-446.
[23] Babak V N,Babak T B,Kholpanov L P. Two-phase absorption complicated by a second-order irreversible chemical reaction in a liquid phase under direct-flow conditions(solution for the fourth quadrant of a hydrodynamic plane)[J]. J Eng Phys Thermophys,1998,71(2):202-213.
[24] Park S W,Choi B S,Lee J W. Chemical absorption of carbon dioxide into aqueous PEO solution of monoethanolamine[J]. Separation Science and Technology,2005,40(16):3261-3275.
[25] Danckwerts P V. Gas-Liquid Reactions[M]. New York:McGraw-Hill,1970.
[26] Mandal B P,Kundu M,Bandyopadhyay S S. Physical solubility and diffusivity of N2O and CO2into aqueous solutions of (2-amino-2-methyl-1-propanol+monoethanolamine) and (N-methyldiethanolamine +monoethanolamine)[J]. Journal of Chemical & Engineering Data,2005,50(2):352-358.
[27] Onda K,Takeuchi H,Okumoto Y. Mass transfer coefficients between gas and liquid phases in packed columns[J]. Journal of Chemical Engineering of Japan,1968,1(1):56-62.
[28] Weiland R H,Dingman J C,Cronin D B,et al. Density and viscosity of some partially carbonated aqueous alkanolamine solutions and their blends[J]. Journal of Chemical and Engineering Data,1998, 43(3):378-382.
[29] Perry R H,Green D W. Perry’s Chemical Engineers’Handbook[M]. 7th ed.New York:McGraw-Hill,2001.
[30] Poling B E,Prausnitz J M,O’connell J P. The Properties of Gases and Liquids[M]. 5th ed. New York:McGraw-Hill,2001.
[31] Snijder E D,te Riele M J M,Versteeg G F,et al. Diffusion coefficients of several aqueous alkanolamine solutions[J]. Journal of Chemical & Engineering Data,1993,38(3):475-480.
[32] Robbins L A. Improve pressure-drop prediction with a new correlation[J]. Chemical Engineering Progress,1991,87(5):87-90.
[33] Ergun S. Fluid flow through packed columns[J]. Chem Eng Prog,1952,48:89-94.
[34] Liu S J. A continuum model for gas-liquid flow in packed towers[J]. Chemical Engineering Science,2001,56(21/22):5945-5953.
[35] Engel V,Stichlmair J,Geipel W. A new model to predict liquid holdup in packed columns-using data based on capacitance measurement techniques[J]. Institution of Chemical Engineers Symposium Series,1997,142(2):939-947.
[36] Sater V E,Levenspiel O. Two-phase flow in packed beds. Evaluation of axial dispersion and holdup by moment analysis[J]. Industrial & Engineering Chemistry Fundamentals,1966,5(1):86-92.
[37] Koho A L,Riesenfeld F C. Gas Purification[M]. 4th ed. Houston:Gulf Publishing Company,Book Division,1985.
[38] Tontiwachwuthikul P,Meisen A,Lim C J. CO2absorption by NaOH,monoethanolamine and 2-amino-2-methyl-1-propanol solutions in a packed column[J]. Chemical Engineering Science,1992,47(2):381-390.
[39] Giese M,Rottschäfer K,Vortmeyer D. Measured and modeled superficial flow profiles in packed beds with liquid flow[J]. AIChE Journal,1998,44(2):484-490.
(责任编辑:田 军)
Reynolds Mass Flux Model and Its Application to Reaction Processes in Packed Bed:Ⅰ. Simulation of MEA-CO2Absorption Process
Li Wenbin,Liu Botan,Yu Kuotsung,Yuan Xigang
(Chemical Engineering Research Center,Tianjin University,Tianjin 300072,China)
The mass diffusion in packed bed under turbulent condition,which is a common operating condition in industry,often shows anisotropy. In the present study,Reynolds mass flux model was applied for simulating the reaction processes in packed bed. The feature of the model is that the modeled Reynolds mass flux equation is used to close the turbulent mass transfer equation,therefore the anisotropic turbulent mass diffusion can be characterized with accuracy. With the proposed model,the distributions of concentration and temperature as well as the velocity were obtained. To validate the present Reynolds mass flux model,simulation of the chemical absorption of CO2into aqueous MEA solution in packed bed was carried out. The simulated results were compared against the open experimental data and satisfactory agreement has been found between them.
packed bed;absorption;simulation;anisotropic turbulent mass diffusion;computational mass transfer
TQ021.4
A
0493-2137(2015)05-0379-09
10.11784/tdxbz201408027
2014-08-11;
2014-10-08.
国家自然科学基金资助项目(21176171,21376163).
李文彬(1986— ),男,博士.
李文彬,richard@tju.edu.cn.
时间:2014-10-28. 网络出版地址:http://www.cnki.net/kcms/doi/10.11784/tdxbz201408027.html.
