基于双目立体视觉与数字散斑图像相关的全场振动测量
2015-06-04陈教豆
陈 忠,陈教豆
(1.上海交通大学 机械系统与振动国家实验室,上海 200240;2.华南理工大学 机械与汽车工程学院 广东省精密装备与制造技术重点实验室,广州 510641)
通过振动测试系统获取机械设备的动态位移等系统动态特性的基本参数,是保证机械正常运行的重要工作。传统的结构振动测试方法采用稀疏的“点”振动测试技术,如加速度传感器振动测试技术、多普勒激光振动测试[1],其测试模型大小受到成本、技术的限制,不能满足现代实验模态测试对测试模型大小的要求。其它的全场光学振动测试方法,如散斑剪切变形[2](DSI)、电子散斑模式干涉[3](ESPI)和全息干涉[4],虽然具有良好的全场振动测试特性,但这些方法存在很难定量或测量精度不高、只能实现单轴的振动测量的问题。
数字散斑相关方法[5-6](DSCM)是根据物体表面随机分布的散斑场在变形前后的统计相关性来确定物体的变形,该方法具有实时、非接触、高精度、全景式测量、对被测物体干扰小等优点。传统的二维数字散斑相关方法(2D-DSCM)只能测量平面物体的二维(面内)位移和应变。为了实现对物体的三维变形测量,Luo等[7]提出了基于双目立体视觉原理和数字散斑相关方法相结合的三维数字散斑相关方法(3D-DSCM)。
针对二维数字散斑相关方法,潘兵等[8]研究了在不同散斑图像中子区大小对测量精度的影响;Tong[9]从抗干扰能力和计算效率两方面研究了各种相关函数的性能,推荐了归一化协方差互相关函数;Schreier等[10-11]详细研究了形函数和灰度插值方法的选择对位移测量精度的影响,目前应用最多的是一阶形函数,高次插值函数具有较高的精度但效率会降低。目前3D-DSCM用于获取物体的三维动态位移与振动频率研究方面,分析各种参数(相关函数、子区大小、形函数)对物体振动频率的影响的相关文献不多。
本文采用双目高速摄像机连续采集散斑变形图像,利用MatchID 3D[12]软件得到图像上散斑的离面位移,再由位移时程曲线求出频率。通过与双频激光干涉仪测量的结果进行对比,验证了三维数字散斑相关方法测量的可行性与可靠性:与双频激光干涉仪测量结果进行比对,考察了三维数字散斑相关方法测量离面位移的精度;分析了相关函数、子区大小、形函数的选择对测量结果的影响。
13 D-DSCM原理
1.1 双目立体视觉原理
双目立体视觉系统类似于人的双眼,用两个摄像机记录同一物体在不同方位下的图像,然后通过匹配左右两幅图像中的对应点得到同一点的视差,再由标定得到的两台摄像机的内外参数得到物体表面的三维形状信息[13]。图1为双目立体视觉模型。

图1 双目立体视觉模型Fig.1 Stereo vision model
图中 P(x,y,z)为物方世界坐标系 OW下一点,O1,O2分别为左右摄像机的光心。P点在左右摄像机中对应的像点分别为P1,P2。如果P1和P2的图像坐标和由标定得到的左右摄像机的内、外参数,就可求得P点在世界坐标系下的三维坐标。
1.2 三维数字散斑相关方法
二维数字散斑相关方法通过相关运算来匹配两幅散斑图像(其中一幅图像作为参考图像,表示为f(x,y);另一幅作为待匹配图像,表示为g(x,y))中的不同子区来得位移场。其基本原理如图2所示,在参考图像f(x,y)中选一个以 M(x0,y0)为中心的(2n+1)×(2n+1)大小的子区,利用子区中的灰度信息,通过一定的相关匹配算法,在待匹配图像g(x,y)中找到以M'(x'0,y'0)为中心的目标图像子区。

图2 变形前后图像子区示意图Fig.2 Schematic diagram of sub-area image before and after deformation
三维数字散斑相关是由二维数字散斑相关方法与双目立体视觉测量结合的一种三维光测力学测量方法。在三维数字散斑相关方法的测量技术中,有两个关键性的技术环节:摄像机标定和匹配。
目前国内外相关研究人员最常用的两种成熟的标定方法是:1986年Tsai[14]提出的经典的两步标定法和1999年张正友提出的Zhang[15]标定法。在三维数字散斑相关方法的测量过程中匹配包含两个环节:二维匹配(左图像变形前、后图像的匹配)和立体匹配(左右图像的匹配),如图3所示。而二维数字散斑相关中关于相关匹配的丰富研究结果可以应用到三维数字散斑相关中的立体匹配中。匹配完成后,对于同一时刻的左右图像对应点,再利用标定得到的双目摄像机内、外参数,根据三角测量原理可以得到目标点的三维坐标信息。
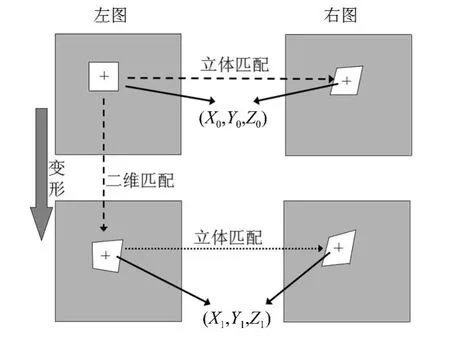
图3 三维数字散斑相关方法匹配示意图Fig.3 Schematic diagram of3d digital speckle correlation method matching
在进行相关匹配时,变形前后的图像以及左右图像需按照某一映射函数来进行相关计算。常用的映射函数有零阶形函数、一阶形函数、二阶形函数等[16]。
零阶形函数表达如下:

一阶形函数表达如下:

二阶形函数表达如下:
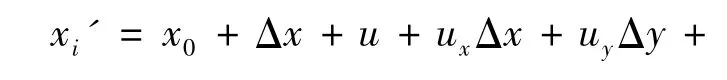

其中:Δx=xi- x0,Δy=yj- y0;u,v分别为子区中心点在x和y方向的位移分量;ux,uy,vx,vy为图像子区的一阶位移梯度;uxx,uyy,uxy,uxy,vxx,vxy,vyy为图像的二阶位移梯度。
评价变形前后图像以及左右图像子区的相似程度,常用的相关函数有归一化互相关、零均值归一化互相关、归一化平方和以及零均值归一化平方和[17],如表1所示。
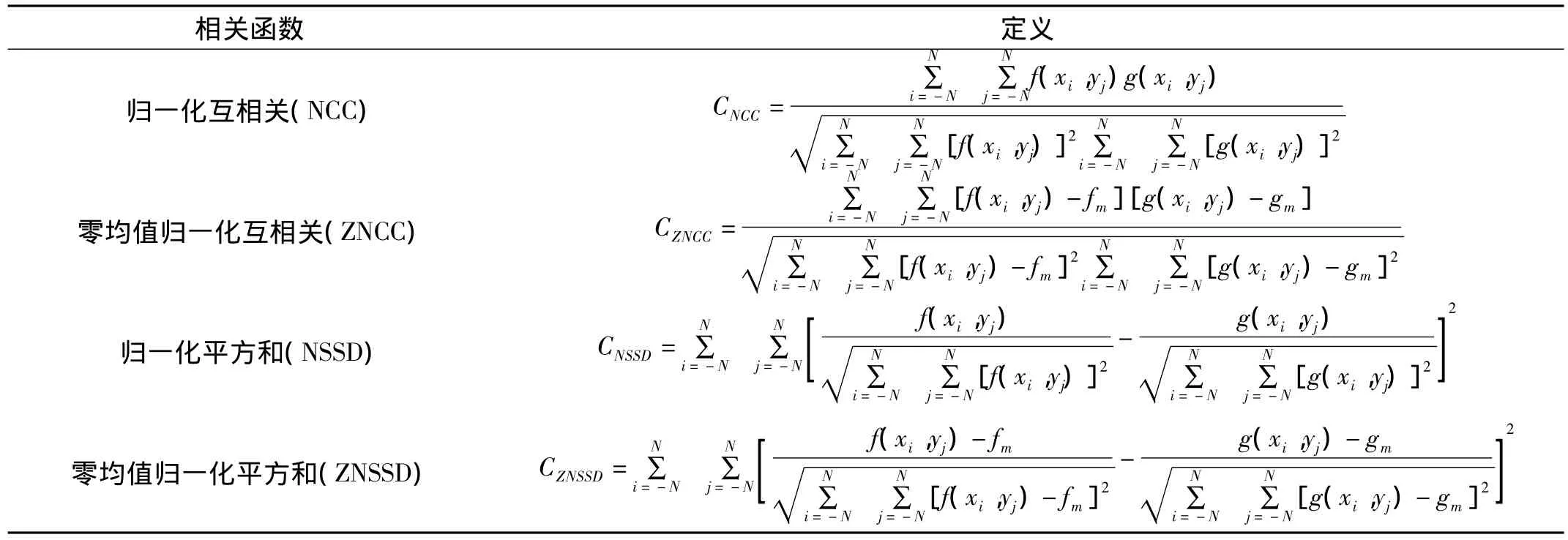
表1 相关函数Tab.1 Correlation Function
表1中,
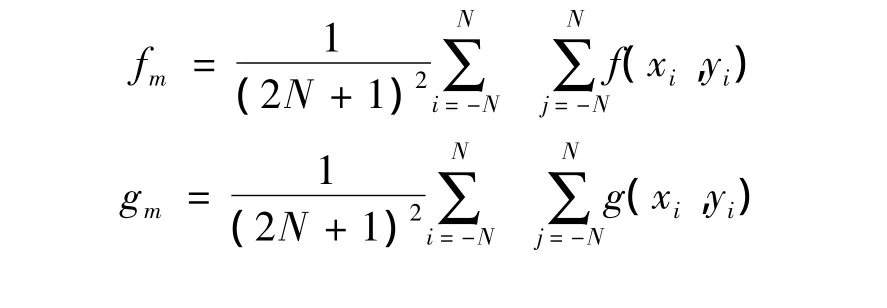
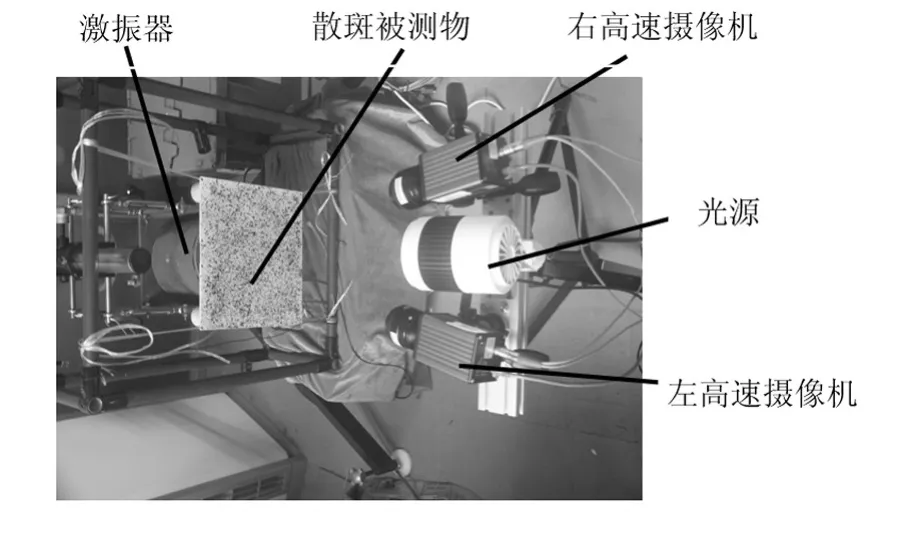
图4 实验系统Fig.4 Experimental setup
ZNCC和ZNSSD的抗噪声干扰能力较强,同时对光强的线性变化不敏感。表1中的相关表达式可用Newton-Rapshon 方法进行优化求解[18]。
2 实验系统与标定
2.1 实验系统
本研究实验系统如图4所示,一块300mm×300mm×2mm的铁板悬挂在一框架上,铁板正面喷有白底黑色散斑点,铁板背后连接着一台激振器,用两台CMOS型的AOS S-PRI F2高速摄像机记录在激励信号下铁板表面不同时刻的散斑图像。
2.2 摄像机标定
本文对双目立体视觉系统的标定是采用HALCON机器视觉软件。图5为左右摄像机拍摄的两幅标定板图像。表2和表3为标定后获得的摄像机的内、外参数。

图5 标定图片Fig.5 Calibration template images

表3 左、右摄像机的相对位置参数Tab.3 Structural parameters of left and right camera
3 实验及分析
先完成双目视觉系统标定,得到双目视觉系统的内、外参数。以正弦信号通过功放驱动电磁激振器激励被测物体,并采用人工外部促发的方式发送TTL信号同步触发两台高速摄像机,使两台高速摄像机同步采集散斑图像。将所得图像用MatchID 3D[15]软件分析处理后,得到被测物分析区域各点在不同时刻的三维坐标,进一步得到分析点的离面位移信息。图6中,小方框为感兴趣区域,选取圆标注的点为分析点。图7(a)为二维匹配结果图,匹配系数在99%以上,图7(b)为立体匹配结果图,可得匹配系数在95%以上,匹配精度满足测试要求。

图6 感兴趣区域与分析点Fig.6 ROI and analyzed point

图7 (a) 二维匹配结果Fig.7 (a)2D-Matching Result

图7 (b) 立体匹配结果Fig.7 (b)Stereo-Matching Result
影响三维数字散斑相关方法的位移测量精度的因素有多种。硬件方面有镜头畸变、散斑模式、摄像机夹角、光照等因素,算法方面涉及到相关函数、图像子区形函数、子区大小、插值方法等。
为了更好地评价数字散斑相关方法的测量准确性与测量精度,本文将由数字散斑相关方法测得的结果与测量精度更高的双频激光干涉仪(RENISHAW XL-80)测得的数据进行比较。
3.1 测量精度的对比分析
采用3D-DSCM和双频激光干涉仪两种方法在正弦波激励下对实验模型测试点进行测量,得到的对比曲线如图8(a)和8(b)所示。
计算测试时间历程信号的有效值,得到激光干涉仪测试数据的有效值I0=0.85977mm,数字散斑法方法测试数据的有效值为I'=0.88678mm。计算相对误差如下:

进一步对幅频曲线做相关分析,得到相关系数corr=0.999058。
可以看出,由双频激光干涉仪和三维数字散斑相关方法得到的位移时程曲线和幅频曲线吻合得很好。

图8 (a) 位移时程曲线Fig.8 (a)The displacement signals in time domain
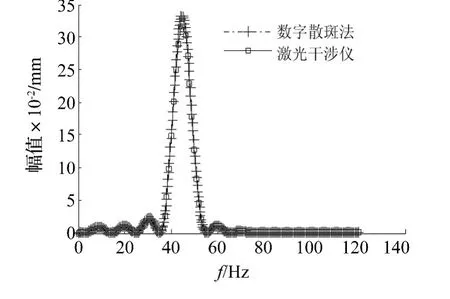
图8 (b) 幅频响应曲线Fig.8 (b)The amplitude-frequency response curves
3.2 对比不同相关函数
采用不同的相关函数(子区大小为21×21)得到的位移时程曲线和幅频曲线如图9(a)、9(b)所示。
将测量得到的数据有效值、幅频曲线与激光干涉仪测得的数据进行比较分析,得到相对误差与相关系数如图10所示。
从图10中可以得到,对于不同的相关函数来说,NSSD和NCC的计算精度较高,ZNSSD和ZNCC的计算精度较低。

图9 (a) 位移时程曲线Fig.9 (a)The displacement signals in time domain

图9 (b) 幅频响应曲线Fig.9 (b)The amplitude-frequency response curves

图10 相关函数对测量结果的影响Fig.10 The effects on measuring results owing to correlation functions
为了研究不同子区大小对测量结果的影响,在其它条件一致的情况下选择不同的子区大小来计算图像感兴趣区域中分析点的离面位移并进行傅里叶变换得到幅频曲线,将测量得到的位移数据有效值、幅频曲线与激光干涉仪测得的数据进行比较分析。在本文中,由于被测物体表面的散斑点较稀疏,在采用5×5~15×15的子区大小时,无法实现很好的匹配效果,故本文选定的子区大小为21×21~91×91,得到相对误差与相关系数如图11所示。图12表示不同子区大小时的匹配耗时。

图11 子区大小对测量结果的影响Fig.11 The effects on the measuring results owing to subset size

图12 匹配耗时Fig.12 Time-consuming of Matching
从图11、12可以得到,随着子区的变大,相应的相关系数都很高且变化很小,计算精度提高,相应的匹配耗时逐渐增加。
3.4 对比形函数
在选择ZNSSD相关函数、41×41大小子区条件下,考虑不同形函数选择下计算目标点的位移与幅频曲线,将测量得到的位移数据有效值、幅频曲线与激光干涉仪测得的数据进行比较分析,得到相对误差与相关系数如图13所示。

图13 形函数对测量结果的影响Fig.13 The measuring effects of shape function
从图13可以得到,随着形函数阶次的提高,相应的计算精度也随之提高,相关系数无多大变化。
4 结论
本文基于双目视觉原理的3D-DSCM方法实现对正弦激励下的物体的全场振动信息测量,将测量结果与双频激光干涉仪测得的数据进行对比分析,证明了进行全场振动测量的可行性。由实验结果可知,相关函数、子区大小、形函数的选择都对计算的精度具有很大的影响。结果可以归纳为:
(1)随着子区大小的增加,位移的计算精度越高,但相应的耗时也会增加,一般计算子区可折中取41×41~61×61;
(2)对于不是很复杂的变形,宜采用NSSD和NCC相关函数,形函数选用一阶就能满足要求。
[1]纪跃波,白永明,黄卫清,等.基于单侧点单方向多普勒激光测头面内振动测试方法[J].振动工程学报,2007,20(3):232-237.JI Yue-bo,BAI Yong-ming,HUANG Wei-qing,et al.Test the in-plane vibration-mode with one-dimensional Doppler laser speed detector for single test-point[J].Journal of Vibration Engineering,2007,20(3):232 -237.
[2]顾国庆,王开福.物体变形测量的相移数字散斑剪切干涉术[J].激光杂志,2011,32(4):16-17.GU Guo-qing, WANG Kai-fu. Digital phase-shifting shearography for measurement of object deformation [J].Laser Journal,2011,32(4):16 -17.
[3]景超,井文才,徐天华,等.用于测振的电子散斑剪切干涉术[J].纳米技术与精密工程,2006,1(4):58-62.JING Chao,JING Wen-cai,XU Tian-hua,et al.Electronic speckle-shering patten interferometry for vibration analysis[J].Nanotechnology and Precision Engineering,2006,1(4):58-62.
[4]周灿林,亢一澜.数字全息干涉法用于变形测量[J].光子学报,2004,33(2):171-173.ZHOU Can-lin,HANG Yi-lan.Deformation measurement by digital holofraphy[J].Acta Photonica Sinica,2004,33(2):171-173.
[5]Pan Bing,Xie Hui-min,Guo Zhi-qing,et al.Full-field strain measurement using two-dimensional savitzky-Golay digital differentiator in digital image [J]. Opt. Eng,2007(3):033601.
[6]Sutton M A,McNeill S R,Helm J D,etal.Advances in twodimensional and three-dimensional computer vision[J].Topics in Applied Physics,Springer Verlag,2000,77:323-372.
[7]Luo P F,Chao Y J,Sutton M A,et al .Accurate measurement of three dimensional displacement in deformable bodies using computer vision[J].Experimental Mechanics,1993,33(2):123-132.
[8]Pan B,Xie H M,Wang Z Y,et al.Study on subset size selection in digital image correlation for speckle patterns[J].Opt,2008,16:37 -48.
[9]Tong W .An evaluation of digital image correlation criteria forstrain mapping applications[J].Strain 2005,41:167-75.
[10]Schreier H W,Sutton M A .Systematic errors in digital image correlation due to undermatched subset shape functions Exp[J].Mech,2002,42:303 -10.
[11]Schreier H W,Braasch J R,Sutton M A.Systematic errors in digital image correlation caused by intensity interpolation[J].Opt.Eng,1999,39:15 -21.
[12]Dimitri Debruyne.MatchID 3D[CP/DK].http://www.matchid.org.2013.12.12/2014.06.22.
[13]Zhang S.Handbook of 3D machine vision:optical metrology and imaging[M].Boca Raton FL:CRC Press.2013.
[14]Tsai R Y.A versatile camera Calibration technique for highaccuracy 3D machine vision methrology using off-the-self TV cameras and lenses[J].IEEE Journal of Robotics and Automation,1987,ra-3(4):323 -344.
[15]Zhang Z Y.A flexible new technique for camera calibration[J].IEEE Transactions on Pattern Analysis and Machine Itelligence.2000,22(11):1330-1334.
[16]Garcia D,Orteu J J,Penazzi L.A combined temporal tracking and stereo correlation technique for accurate measurement of 3D displacements:application to sheet metal forming[J].Journal of Materials Processing Technology,2002,125:736-742.
[17]Pan B,Qian K,Xie H,et al.Two-dimensional digital image correlation for in-plane displacement and strain measurement:A review[J].Measurement Science and Technology,2009,20:062001.
[18]潘兵,谢惠民.数字图像相关中基于位移场局部最小二乘拟合的全场应变测量[J].光学学报,2007,27(11):1980-1986.PAN Bing,XIE Hui-min.Full-field st rain measurement based on local least2square fit ting for digital imagecorrelation met hod[J].Acta Optica Sinica,2007,27(11):1980-1986.
