科技创新与黑龙江省服务外包产业升级
2015-06-02于珊珊姜鹏
于珊珊 姜鹏
[摘 要]通过对黑龙江省主要城市科技创新资源与创新活动空间集聚指数进行测算,比较全省各地级城市科技创新的空间分布差异,并通过计算全局和局域空间自相关指数,检验黑龙江省创新活动的空间相关性,利用空间面板数据分析方法构建黑龙江省科技创新溢出效应计量模型,考察相关影响因素对科技创新溢出效应的贡献度,科技创新R&D资本投入对科技创新产出的影响程度呈现上升趋势,而科技创新人员投入的重要性日趋减弱。为增强黑龙江省科技创新资源与要素调整与配置效率,应鼓励不同行业资金融合支持科技创新活动,构建多元化的科技创新资金结构,逐步提高科技创新活动资金筹集的市场化程度。
[关键词]黑龙江;科技创新;溢出效应;服务外包
[中图分类号]F062.9 [文献标识码]A [文章编号]2095-3283(2015)04-0011-06
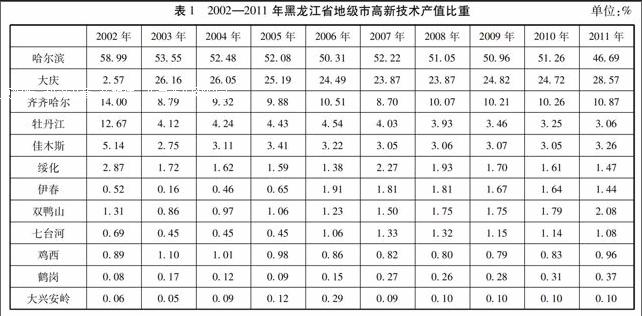
当前国际经济活动的一个显著特征是国际产业转移从制造业向服务业延伸,作为一种具有高成长性、高附加值和促进区域协调发展的新的国际分工形式,服务外包在全球范围内得到了迅速发展。科技创新有利于服务外包产业从低附加值向高附加值领域转移。黑龙江省科技资源富集、科技综合实力较强,但科技创新活动与创新产出存在明显的空间地理集聚现象。除2002年外,2003—2011年黑龙江省各地级城市高新技术产值占全省比重排序前三位的分别是哈尔滨、大庆、齐齐哈尔,这三座城市是黑龙江省西部地区“哈大齐工业走廊”的主体城区,其高新技术产值总和占当年全省高新技术产值总和的比重均超过了80%(如表1所示)。2002—2011年黑龙江省主要城市高新技术产值绝对数量的变化以哈尔滨、大庆两地最为显著,这两地高新技术产值增长速度明显快于全省其他地区。由此可知,黑龙江省科技创新活动存在明显的空间分布异质性。
一、研究方法
(一)空间集聚测度方法
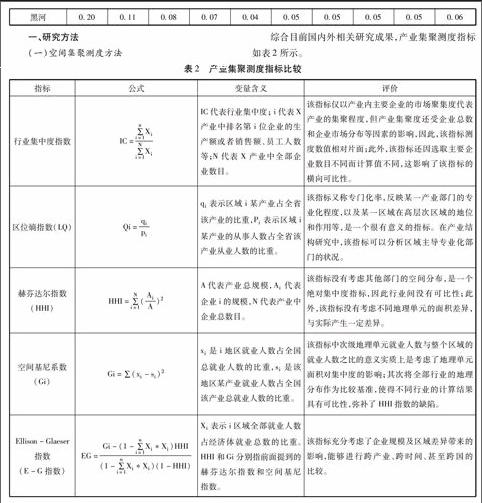
综合目前国内外相关研究成果,产业集聚测度指标如表2所示。
通过对以上指标的比较分析,考虑地理单元因素、产业空间分布差异可比性因素等,结合本文搜集整理的数据,选择区位熵指数(LG)和空间基尼系数(Gi)衡量黑龙江省科技创新的集聚程度。
(二)空间相关性指标
根据地理学第一定律,地理距离相近地区的市场经济运作活动、科技研发与交通往来,相比地理距离较远地区具有显著的关联性。目前测度空间相关性的指标,通常采用全局空间自相关指标Global Morans I指数和局域空间自相关指标Local Morans I指数。Global Morans I指数是衡量各个区域间的整体的空间差异程度和空间关联的分析方法,其来源于统计学的Pearson相关系数,将互相关系数推广到自相关系数,时间序列的自相关系数推广到空间序列的自相关系数,最后采用加权函数代替滞后函数,将一维空间自相关系数推广到二维空间自相关系数,即可得到Global Morans I指数。Global Morans I指数的实质是标准化的空间自协方差。局域空间自相关Local Morans I指数是检验局部地区是否存在相似或相异的观测值聚集的指标。它可以度量某地区与其周围地区存在的空间差异程度和以及显著性,它可以理解为Global Morans I的分解。Global Morans I指数和Local Morans I指数的具体计算公式为:
(三)空间计量模型
综合目前国内外相关研究成果,考虑空间因素的知识溢出效果模型主要包括两种空间计量形式(Anselin,1996),一种是空间滞后模型(SLM),该模型反映了各变量在一地区是否存在扩散现象(溢出效应);另一种是空间误差模型(SEM),该模型反应了存在于扰动误差项之中的空间依赖作用,用以衡量邻近地区由于因变量的误差扰动对本地区观察值的影响程度。SLM空间计量模型的形式如公式(1)所示,SEM空间计量模型的形式如公式(2)所示:
公式(1)中,y为因变量,X为外生解释变量,Wy为空间滞后因变量,ρ为空间回归系数,用于衡量地理溢出程度,β反映了自变量X对因变量y的影响,ε为随机误差向量;ε为随机误差向量。公式(2)中λ为空间误差系数,用于衡量样本观察值的空间依赖作用,μ为正态分布的随机误差向量,参数β反映了自变量X对因变量y的影响。
目前研究知识生产与科技创新的影响与溢出效果,主要利用Griliches -Jaffe提出的基于柯布—道格拉斯生产函数的标准知识生产函数,函数基本形式为:
公式(3)中Q代表科技创新产出,A代表常数项,R&D为科技创新的经费或人力资本投入,S代表影响科技创新产出的经济社会变量,ε为随机误差项,i为观测单元,t为时间。本文考虑到数据的获取性与可得性,将以公式(3)中各项变量分别定义为黑龙江省主要城市R&D经费投入K、黑龙江省主要城市科技创新人员投入L、黑龙江省科技创新的外部知识溢出变量S。在具体实证研究过程中,还需要对以上公式两边取对数,构建双对数模型,即
二、数据来源与处理
本文研究对象为黑龙江省11个地级市和2个地区,根据目前相关文献研究经验,一般采用专利申请数量作为科技创新能力衡量指标,但由于统计数据的可得性与数据量纲的一致性,本文选取高新技术产值替代专利申请数量作为衡量研究对象地区科技创新产出的评价指标,R&D经费支出以及R&D人员投入作为衡量研究对象地区科技创新投入水平的评价指标。本文数据来源于《黑龙江统计年鉴》,黑龙江省科技统计网、黑龙江科技信息网等。部分年份数据缺省值采用线性插值法进行补全。本文空间统计分析与空间制图采用Arcgis软件,空间相关性检验与空间计量分析采用Geoda软件。
三、实证分析
(一)空间集聚实证结果分析
根据区位熵指数(LG)、空间基尼系数(Gi)计算公式,黑龙江省主要城市2003—2010年科技创新两项指标的计算结果如表3、图2所示。其中区位熵指数(LG)大于1的城市以齐齐哈尔、大庆、哈尔滨为主,表明这些地区科技创新的专业化水平明显高于全省其他地区,人均科技创新创新效率相对显著,尤其是齐齐哈尔地区,除2007年外,其他年份LG指数均高于1,LG指数平均值为2.159,位居全省第一位。空间基尼系数(Gi)在2003—2007年始终保持在0.08水平上下浮动,但从2008开始,Gi系数显著上升,始终保持在大于0.1水平浮动,Gi系数平均值约为0.1,表明全省科技创新活动空间分布存在一定差距,但从数据上来看,差距程度与发达国家相比,差距相对较小。综合以上两项指数的测算结果,黑龙江省科技创新活动的空间分布并不均匀,呈现一定的局部集聚性,并且这种地理集聚度随着时间的推移呈现出逐渐增加的趋势。endprint
(二)空间相关性实证结果分析
根据全域空间自相关指数和局域空间自相关指数计算公式,本文在计算过程中空间权重矩阵采用“K-Nearest Neighbor”法,通过Geoda软件,计算2002—2011年黑龙江省11个地级市和2个地区科技创新产出的全局空间自相关指标的Morans I值与局域空间自相关指标的MoranI值,以及它们的显著性检验值如表4、图3所示。
根据表4可知,2002年全局Morans I指数和局域Morans I指数值相对较低,表明空间相关性相对较弱,且未通过5%显著性检验。而2003—2011年全局Morans I指数和局域Morans I指数的平均值为0.1045,P-value通过了5%显著性检验。因此,2003年以后,黑龙江省主要城市科技创新产出的空间相关性尤为明显,尤其是2011年,全局Morans I指数和局域Morans I指数值达到了0.1162,实现了2003年以来的显著上升。
2002—2011年黑龙江省13个市(地)以高新技术产值衡量的科技创新产出的全局Morans I指数和局域Morans I指数曲线的变化,除2002年Morans I指数为负值,且仅通过10%水平的显著性检验,而未通过5%水平的显著性检验之外,2003年开始Morans I指数显著上升,虽然此后经历了小幅下降,但2004—2010年,MoranI指数均保持在0.1水平稳定波动,且均通过了5%水平的显著性检验,尤其是2011年,MoranI指数实现了显著的上升反弹,表明空间自相关性更为明显。正向的空间自相关性表明随着经济的发展,黑龙江省主要城市之间的经济活动的空间相关性不断提高,即一个城市的科技创新投入、产出将会对相邻城市产生正向的溢出效应。
图3是2003年、2006年、2009年、2011年黑龙江省13个市(地)科技创新的MoransⅠ散点图,图中横轴代表该观测单元的科技创新产出,纵轴代表周边观测单元的科技创新产出。第一象限(HH)表示高—高的正空间自相关,代表观测地区的科技创新产出较多,周边观测地区的科技创新产出也较多;第二象限(LH)表示低—高的空间自相关关系,代表观测地区的科技创新产出较少,而周边观测地区的科技创新产出较多;第三象限(LL)表示低—低的空间自相关关系,代表观测地区的科技创新产出较少,周边观测地区的科技创新产出也较少;第四象限(HL)表示高—低的空间自相关关系,代表观测地区的科技创新产出较多,而周边观测单元的科技创新产出较少。
如图3、表5所示,2003年、2006年、2009年、2011年黑龙江省主要城市科技创新的 Morans I散点分布极为相似,除2003年,齐齐哈尔市科技创新的空间自相关性由第二象限变动至第一象限外,其他3个年份各象限的分布地区均相同。即第一象限(HH),表示以大庆与哈尔滨不仅各自地区科技创新产出相对较强,同时对周边地区也起到辐射和带动作用,使相邻地区的创新产出也较多,具有正的空间相关性;第二象限(LH),表示齐齐哈尔、绥化、牡丹江三个地区尽管靠近科技创新产出较强的地区,但由于缺乏吸纳科技创新扩散或溢出效应的能力,各自暂未受到周边地区的辐射影响,科技创新产出较少;第三象限(LL),表示鸡西、伊春、鹤岗、大兴安岭、黑河、佳木斯、七台河、双鸭山地区的科技创新产出相对较少,同时相邻地区的科技创新能力也相对薄弱,并没有产生积极的正向互动影响效应。
(三)空间计量实证结果分析
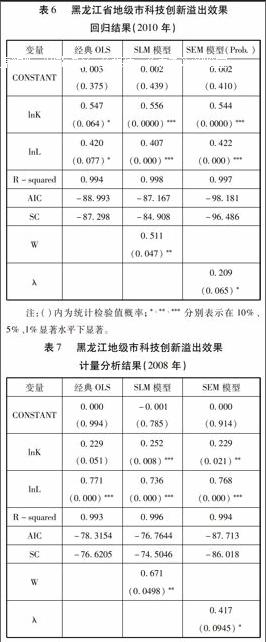
通过验证,本文选择滞后5期模型估计效果最好,同时又根据本文整理的空间计量数据时间范围2003年至2010年,本文选择2008年和2010 年黑龙江省11个地级市和2个地区的横截面数据为例衡量科技创新的空间溢出效果,具体经典OLS模型、空间滞后模型(SLM)、空间误差模型(SEM)回归结果如表6、表7所示。
由表6和表7可知,SLM 模型和SEM 模型与经典OLS 模型相比,各项指标检验值均具有显著性,2010年三种模型的拟合优度R2与2008年相比,均小幅上升,但SLM模型与SEM模型的拟合优度R2的绝对值略高于经典OLS模型的拟合优度,此外,SLM模型和SEM模型的空间相关系数都为正,且都通过了1%的显著性水平检验,这表明黑龙江省11个地级市和2个地区,以高新技术产业衡量的科技创新产出具有显著性的空间正相关效应。而经典OLS模型由于未考虑空间相关性,其回归结果中各项指标的解释能力明显弱于SLM模型和SEM模型。进一步比较SLM模型与SEM模型,SLM模型2010年和2008年的拟合优度R2均略高于SEM模型。此外,2010年和2008年SLM模型的赤池信息准则(AIC)和施瓦茨准则(SC)分别小于SLM模型相应指标值,因此 SLM 模型是上述三个模型中的最优回归模型。
根据以上空间计量模型拟合结果,验证了黑龙江省主要城市和地区的科技创新活动存在一定的空间相关性和依赖性,且空间滞后模型(SLM)能够很好地解释科技创新投入与科技创新产出之间的空间影响性。根据表6和表7测算结果,SLM模型中,科技创新R&D资本投入和科技创新人员投入均通过了1%水平下的显著性检验,且2010年科技创新R&D资本投入的弹性系数值明显高于2008年的系数值,这表明科技创新R&D资本投入对科技创新产出的影响程度呈现上升趋势,R&D资本投入的重要性日益凸显;而2010年科技创新人员投入的弹性系数值明显小于2008年的系数值,这表明科技创新人员投入对科技创新产出的影响程度逐年呈现下降趋势,科技创新人员投入的重要性日益减弱,因此SLM 模型更强调R&D资本投入对科技创新产出的贡献作用,由此可知,黑龙江省主要城市和地区应积极加大科技创新的财政投入,正确引导社会科技创新资金投入与流通,积极拓展多渠道、多层次的科技创新融资方式,鼓励不同行业资金融合支持科技创新活动,构建多元化的科技创新资金结构,逐步提高科技创新活动资金筹集的市场化程度。
[参考文献]
[1]王力,刘春生,黄育华.中国服务外包竞争力报告(2012—2013):中国服务外包基地城市竞争力评价[M]社会科学文献出版社,2013.
[2]王晓红.中国服务外包:跨越发展与整体提升[M]山西经济出版社,2012.
[3]陈斐.区域空间经济关联模式分析理论与实证研究[M]中国社会科学出版社,2008.
(责任编辑:张彤彤)endprint
