无线传感器网络部署优化仿真研究

郎健 孟晗

【摘 要】目前，基于WSN节点部署仍然存在部署成本高，网络覆盖范围低的问题。本课题针对以上问题，提出一种改进的WSN节点部署优化算法，在一定数量传感器节点和一定监测区域内，最大限度地提升网络覆盖率，降低部署成本，提高网络QOS。本算法将微粒群算法和K-means算法应用到无线传感器部署问题，并提出了KMPSO算法的改进算法（TKMPSO）。

【关键词】微粒群算法 K-means均值聚类算法 WSN

1 WSN节点部署算法国内外研究现状

无线传感器网络（WSN）是由大量具有通信和计算能力的传感器节点以自组织和多跳的方式构成的无线网络，能够协作地感知、采集、处理和传输网络覆盖区域内感知对象的监测信息，并将其报告给用户[1]。文献[2]和文献[3]都提出了一种基于微粒群算法的无线传感网络部署优化方法，虽然证明微粒群算法能够有效实现无线传感网络部署优化，但是标准粒子群算法在空间搜索时，容易陷入“早熟”现象，达不到理想的覆盖率。针对该问题，有文献提出一种基于改进微粒群算法（KMPSO）的无线传感器网络节点部署优化策略。在优化的过程中，算法通过引入K-means聚类算法，将种群划分为几个子种群，使各子种群之间彼此进行独立优化；与此同时，为了避免“早熟”发生，可以增强子种群间的信息交流，对子种群进行动态重组，减弱微粒对局部最优点的追逐，避免标准PSO算法中的粒子“早熟”现象，但是该算法规定迭代若干代后，强制对子种群进行动态重组，具有一定的盲目性。

针对K-means微粒群算法存在的问题，本文提出一种改进TKMPSO算法。

2 改进的KMPSO算法（TKMPSO算法）

郑磊等人提出KMPSO算法能有效地避免“早熟”现象，但是仍然存在不少的问题，为了解决这些问题，本文提出KMPSO算法的改进算法（TKMPSO），同样采用PSO和K-means算法结合的方式。算法中每一个微粒表示区域内全部传感器节点的一种部署方案。TKMPSO算法的基本思想：首先，引入K-means聚类算法将种群划分成几个子种群，每个子种群独立进化，假设T表示不合格的全局最优值的连续累计次数，如果T达到阈值，对子种群进行重新划分，组成新的微粒群。再次，算法引入基于欧几里得距离矫正算法，降低节点之间覆盖重叠区域的面积。

2.1 基于欧氏距离的矫正算法

通过实验，作者发现在标准PSO算法进入迭代后期（2/3倍最大迭代周期），一些微粒中的节点之间存在扎堆的情况，造成了大量感知区域重叠，大大降低了全局覆盖率。为了解决上述问题，进一步提高覆盖率，本文引入了一个基于欧氏距离矫正算法。

本算法的中心思想是：遍历微粒群中每一个微粒，从微粒j中头节点i（1

将区域按照直角坐标系的规则划分为4个面积相等的象限。根据节点的x、y坐标定位到某个象限，如果是第一象限，将该节点向更靠近上边界或者右边界的方向移动r/2的距离。

如果是二象限，将该节点向更靠近上边界或者左边界的方向移动r/2的距离。如果是三象限，将该节点向更靠近下边界或者左边界的方向移动r/2的距离。如果是四象限，将该节点向更靠近下边界或者右边界的方向移动r/2的距离。然后，判断节点k到第k1（1

（1）在采用KMPSO算法对一个微粒优化之后，判断是否进入后期迭代，100代以后成为进入迭代后期。如果是迭代后期，进入步骤2，开始扫描微粒到其它粒子之间的距离。（2）判断是否还有未遍历的微粒节点，若是，进入步骤3，开始矫正当前节点的位置。否，则已完成所有节点的遍历，结束矫正算法。（3）判断当前微粒i到其它每一个微粒之间的距离是否满足算法规则即大于R。是，则进入步骤2。否则，进入步骤4，对不满足条件的一个节点j单独变异。（4）采用PSO算法更新位置的策略对节点j进行变异，让其到每一个其它节点的距离小于R/2。采用while循环语句实现，若结束，则跳转到步骤3。

2.2 网络模型

为了进一步介绍该算法的原理和实现该算法的仿真实验，我们先对算法建立网络模型。

每一个传感器节点采用 表示（0

因此，传感器节点集C所覆盖的像素面积之和就是该节点集中所有节点覆盖像素点的并集，记为Sarea，则 。无线传感网络节点部署的优化目标是使网络的覆盖率最大，即 。定义适应值函数如下： 。当 取得最大值时的节点位置信息就是无线传感器网络中节点的最佳部署位置。

2.3 TKMPSO算法实现流程

（1）使用K-means算法将微粒群划分为k个种群，并得到每个子种群的聚类中心。（2）初始化阈值和计数器变量，通过最有目标函数计算微粒的最优位置和最优适应值，并用聚

类中心初始化全局最优位置和全局最优适应值变量。（3）开始一轮进化，若进化到迭代后期，则采用基于欧氏距离的矫正算法调整。否则，PSO算法更新微粒。然后，若微粒前适应值大于其个体最优值，则进入4；否则，采用连续无变化变异算法对微粒进行变异处理。

（4）更新微粒的pbest_fit后，若大于gbest_fit，则更新gbest_fit，否则，将小于子种群中gbest_fit的微粒数量gCount+1。（5）若所有的微粒结束一代进化，则重复步骤3，进行下一个微粒的进化。否则，进入6。（6）若gbest_fit无变化的节点总数大于微粒总数的2/3倍，则认为这一代的gbest_fit不满足进化要求，将不合格次数thresCounter加1。进入下一步。否则，thresCounter重置为0，进入第8步。（7）若thresCounter≥gThres，K-means算法将微粒群重新划分为k个种群，进入第8步。（8）gCount=0。更新公式动态更新惯性权重因子w和自适应因子C1，C2。若达到进化次数要求，则输出最优适应值，结束算法。否则，进入下一代进化，执行步骤3。

3 Matlab仿真

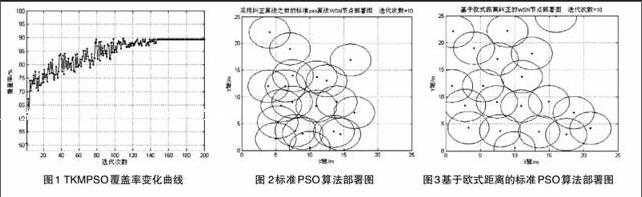
本文设计了2组模型对实验进行测试。第1组反映了TKMPSO算法的覆盖率变化曲线结果（见图1），第2组反映了欧氏距离的矫正算法处理以后传感器节点结果（见图2、3）。

图1 TKMPSO覆盖率变化曲线 图 2标准PSO算法部署图 图3基于欧式距离的标准PSO算法部署图

图1反映了TKMPSO算法的传感器节点部署图，覆盖率提高到89.49%，与初始覆盖率相比，网络覆盖率提高了76.51%。在前120次的迭代过程中，曲线的斜率较大，覆盖率增长较快；超过120次以后，曲线的斜率明显变小，覆盖率增长缓慢，最终在147代左右趋于一个稳定的常数。这是因为在惯性系数因子的作用下，算法在早期具有较强的全局收敛能力。随着迭代次数的增加，微粒开始在最优位置附近振荡。图2，图3反映了标准采用欧式距离矫正算法的优化结果。覆盖率从51.93%提升到67.26%。由此可见，基于欧式距离的矫正算法显著地提高网络覆盖率，能够有效地避免传感器节点扎堆现象。

4 结语

在标准PSO算法的基础上，郑磊提出了基于KMPSO微粒群算法，本文在KMPSO的基础上提出一种改进算法（TKMPSO）。主要从如下几方面提出改进方案：首先，引入粒子群聚类阈值变量，科学的控制采用K-means算法动态划分微粒群粒子的时机。其次，为了解决感知区域重叠的问题，本文引入基于欧几里得距离矫正算法，对距离不符合要求的两个节点使用PSO算法进行变异。最后，通过matlab仿真实验证明，TKMPSO算法达到了预期的效果。

参考文献：

[1] AKYILIDIGIF，SU Wei-lian，SAN KARASUBRAMANIAMY，etal. A survey on sensor networks [J].

IEEE Communications Magazine ，2002，8 ： 721-734.

[2] 任彦，张思东，张宏科.无线传感器网络中覆盖控制理论与算法.[J].软件学报，2006，17（3）： 422-433.

[3] BURNERA，BUCZAKAL，JIN Yao-chu. A self-organizing，cooperative sensor network for remo te surveillance：current result[C] //Proceedings of SPIE Volume 3713. Bellingham ，WA ： SPIE，1999 ： 238-248.