在高等数学课程中开展数学实验教学的探索与研究

高 洁，周 玮

（1．潍坊学院 数学与信息科学学院，山东 潍坊 261061；2．济南工程职业技术学院 基础部，山东 济南 250200）

在高等数学课程中开展数学实验教学的探索与研究

高 洁1，周 玮2

（1．潍坊学院 数学与信息科学学院，山东 潍坊 261061；2．济南工程职业技术学院 基础部，山东 济南 250200）

对在高等数学课程中开展数学实验教学的内涵、教学内容、教学设计、教学实施以及评价方法进行深入研究．结合高等数学教学内容设计了数学实验内容，将数学实验分为基础实验和建模实验，通过具体实例说明了应用Mathematica软件进行数学实验的关键步骤，并对数学实验的具体实施进行了详细论述．

高等数学；数学实验；数学建模；Mathematica软件

高等数学是高等学校一门重要的基础学科，是理工科大学生的必修课，它不仅是各学科共同使用的精确的科学语言，也对学生后继课程的学习及思维素质的培养起着重要作用，它已经日益成为各学科和工程实践中解决实际问题的有力工具．高等数学教学的根本任务就是要通过教学活动让学生学习掌握数学的思想、方法和技巧，并能学以致用，这就使得通过高等数学的学习不仅要培养大学生具有坚实的数学理论和较高的数学技能，而且同时要提高他们自觉运用高等数学理论知识去解决相关专业中的实际应用问题的数学构建能力．

目前在许多高等院校高等数学的教学依然沿用传统的讲授式教学模式，这种模式固然可行但也存在一定的弊端：一是传统的数学教学重理论轻应用，学生感觉枯燥无用；二是以教师讲授为主的教学方式造成学生被动地学，不利于学生独立思考和学习能力的培养；三是单纯讲解书本知识与专业脱节，学生体会不到数学在专业学习中的重要作用，不利于学生应用数学解决实际问题能力的培养，更不利于学生创新精神和创造能力的培养[1]．针对这种状况，近十几年来许多院校对高等数学课程的改革进行了一些讨论和探索，提出了调整优化教学内容和体系，开设数学实验和数学建模课的设想，还有许多文献研究了数学建模和数学实验的系统模式，对如何通过这门注重理论联系实际的课程培养学生的想象力、洞察力、直觉思维、发散思维、动手能力，以及应用能力和创新能力进行了探索[2]．但是这些文献普遍缺乏具体的实施措施和评价标准，同时由于各个学校的师资、生源、设备等条件的不同，也为数学实验教学带来了一定的困难．借鉴国外“从做中学”的教学模式[3]，在完成高等数学基本教学任务的同时，将数学实验教学融入高等数学课程中，不仅在平时教学中增加数学实验内容，还定期进行上机实验，使高等数学课程从“学数学”向“用数学”转变，从“理论教学”向“应用教学”转变，从“手工计算”向“应用计算机软件计算”转变，充分展现数学的工具性和应用性，并在实践中不断总结经验教训，对在实验课程中介绍哪些内容、怎样实施、如何对学生进行评价进行了探索和研究．

1 数学实验的内涵

数学实验是在计算机系统的帮助下，利用数学软件工具解决数学问题的一种教学手段，是将数学科学转化为数学技术的主要途径[4]．数学实验需要在安装数学软件的计算机机房进行，是高等数学课堂教学的补充，它既可以作为一门独立的课程，也可以融入到数学课堂教学中，作为课堂教学内容的一部分．数学实验包括基础实验和建模实验，基础实验是注重基本数学运算的实验；建模实验是注重解决实际问题的实验．每个实验专题都由实验目的、实验准备、实验任务、实验过程、思考与练习5个部分组成，其中的实验任务是实验专题的核心，由“基础实验和建模实验”共同组成．数学实验将数学知识、数学建模与计算机应用有机地结合起来，使数学不仅仅局限于数学的证明和计算技巧的训练，而是更注重于借助数学软件解决专业实际问题[5]．

2 数学实验的教学设计

2.1 数学软件的选取

数学实验可选用多种数学软件，Mathematica软件系统是目前世界上应用最广泛的符号计算系统之一，提供了与Matlab和Maple等著名数学软件同样强大的功能，主要功能包括3个方面：符号演算、数值计算和绘图．由于Mathematica界面直观、文件小巧，易于安装，因此研究者将Mathematica软件包作为主要教学内容．

2.2 数学实验内容和高等数学教学内容的关系

将Mathematica软件包融入到高等数学各章节的计算方法中，只要求学生掌握高等数学计算的原理和最基本的计算方法，对需要应用技巧或计算量比较大的计算，要求学生应用数学软件解决．高等数学课时有限，将数学软件的计算方法适时引入，不仅可以节省大量用于介绍各种计算方法和计算技巧的课时，而且可以提高解题速度和解题的准确度．学生在专业实际问题中遇到的数学计算往往数据量大，复杂度高，如果没有数学软件，那么没有一定数学功底的人是算不出来的．现在学生借助计算机解决了计算问题，就可以把精力投入到分析问题的过程中[6]．在高等数学每个单元教学中增加数学建模实验内容，就是让学生体验数学工具在实际应用中的作用，借助数学软件应用数学解决实际问题，提高数学应用能力．下面以积分与应用为例说明如何结合高等数学进行数学实验．

（1）实验目的．

理解不定积分、定积分的概念，熟练掌握Mathematica软件求不定积分、定积分的命令，并会运用数学软件解决实际问题．

（2）实验准备．

Integrate[f, x]计算函数f [x]的不定积分，也可以使用BasicInput模板上的不定积分符号；

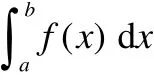
（3）实验任务．

基础实验：求函数的不定积分和定积分的Mathematica软件命令

建模实验：暴雨期间平均降雨量问题

某地区在夏天经常受到暴雨的侵害，为了做好灾害的预防工作，通过以往暴雨期间的统计资料，得出一条河流在延续了12.5小时暴雨期间的流量曲线（如图1），暴雨覆盖的面积是100 km2，计算在暴雨期间的平均降雨量是多少[7]？

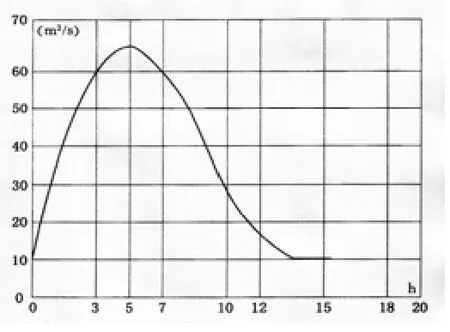
图1 暴雨降水量

（4）实验过程．

基础实验过程是要求学生在计算机上利用Mathematica软件运行不定积分和定积分的命令，得出结果．建模实验则需要对实际问题进行分析，建立数学模型，再利用Mathematica软件进行计算．

（5）思考与练习．

通过实验体会数学软件的运行方法，总结有几种方法可以实现积分计算，并思考如果数学软件命令不能求出某函数的原函数，是否说明该函数不可积，当定积分函数中含有参数，数学软件命令能否对其求定积分．通过思考与练习熟练掌握数学软件的应用．

2.3 数学实验内容的课时分配

数学实验内容包括数学基础实验和数学建模实验两部分，基础实验主要以数学软件的学习和应用为主，运用Mathematica软件进行求导、积分、求解微分方程、级数等计算．数学建模实验是以实际问题为载体，运用数学软件工具解决实际问题，主要培养学生的探究能力、创新能力和应用能力[8]．数学实验具体内容和课时分配如表1：

表1 数学实验具体内容和课时分配

3 数学实验的教学实施

3.1 基础实验的教学

（1）以Mathematica的符号运算系统为依据，掌握算微积分的计算．

高等数学中微积分教学的一个重点就是极限、导数、积分的计算方法，这一部分公式多，技巧性强，虽然教师在计算技巧的讲解上花费了大量的课时，学生仍然感觉学习困难．Maryland大学的M. Kathleen Heid是最早运用Mathematica调整微积分课程结构的，传统课程的学生必须学会微积分计算技巧才能考虑更多的应用，而计算机的使用可以使学生在掌握计算技巧之前就能利用计算机解决应用问题[9]，Mathematica强大的计算功能使微积分的计算变得非常简单，结合Mathematica数学实验进行微积分的教学，不仅可以提高学生学习兴趣，还可以提高学生的学习效率，在有限的课堂教学时间内使学生掌握更多的数学知识和计算技能．

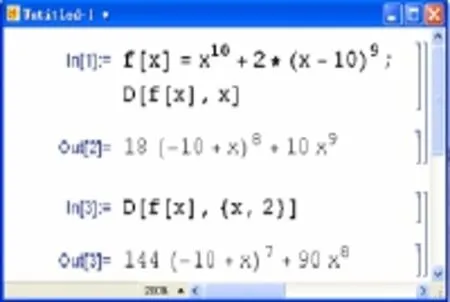
图2 计算（一）

图3 计算（二）

（2）验证高等数学中的定理公式，加深对数学知识理解．

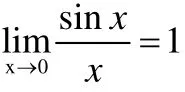
图4 函数图像（一）

图5 函数图像（二）

再利用Mathematica解方程，得出ξ值，如图6．

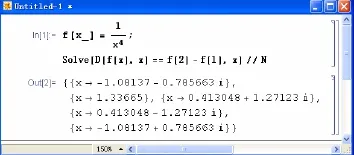
图6 计算（三）

其中的实数解就是满足拉格朗日中值定理的ξ，约为1.336 65．

（3）将数值计算与数学建模相结合，提高数学的应用能力．

数值计算方法是一种研究并解决数学问题的数值近似解的方法，是在计算机上使用的解数学问题的方法，数值计算方法的计算对象是微积分、线性代数、常微分方程中的数学问题，包括插值和拟合、数值微分和数值积分、求解线性方程组的直接法和迭代法、常微分方程的数值解等问题．数值计算是从理论到实际的一个重要桥梁，在计算机成为数值计算的主要工具以后，应用数学方法解决实际问题的过程变为：实际问题→数学模型→计算方法→程序设计与上机计算[10]．数值分析主要研究数学问题的数值方法和理论，数学建模通常作为应用数学的任务，数学实验为数学建模内容的教学提供了工具．数值计算是比较复杂的算法，学生在学习上往往感觉比较枯燥，将数值计算与数学建模结合起来，对于与学生所学专业有关的问题，他们迫切地想了解如何通过数学方法获得问题的解答，因此可以增强学生的学习积极性，应用Mathematica软件进行计算减少了计算的复杂性，可以帮助学生顺利解决实际问题，对提高学生的数学应用能力有很大帮助．

3.2 建模实验的教学

建模实验也称为运用数学技术的探索性实验，是联系数学与实际问题的桥梁，是数学实验从广度和深度上的进一步深入和提高，它为学生提供了自主学习的空间，有助于学生体验数学的价值和作用，有助于激发学生学习数学的兴趣，发展学生的创新意识和实践能力．

建模实验内容一方面来自教材中的问题原型，另一方面来自生活和专业实际问题．数学作为思想与技术兼顾的学科主要是为了解决实际问题，而数学建模正是通过识模、析模、建模、解模、验模的过程，将实际问题数学化，通过使用数学工具来解决实际问题[11]．

在建模实验教学中应注重实验的适当性、开放性和趣味性，把握好以下几个教学环节：

（1）创设问题情境，把握问题的适当性．

高等数学实验中的数学建模问题应尽量结合专业，结合生活实际，可以从教材中搜集素材，挖掘教材中数学问题的生活模型，也可以是专业问题，比如在学完导数应用中的最值问题时，可以引导学生讨论最佳订货批量问题．教师创设问题情景，工厂为了生产必须储存一些原料，如果把全年所需原料一次性购入，则不仅占用资金、占用库存，还会增加保管成本．但是如果分散购入，则因每次购货都会有固定成本（与购货数量无关），而使费用增大．现在希望找到一个两全其美的订购原料的方案．针对这一问题要求学生建立模型并求解．在设计数学建模实验内容时，应尽量结合学生已学的课程内容，所选问题难度适中，数值处理过程也应当较为简单，降低数学建模的“门槛”，使数学建模任务接近大多数学生的数学水平．

（2）以小组交流学习为主，体验数学的应用价值．

数学建模问题由于其条件和结果的开放性，需要花费较多的时间思考，因此实验任务一般在课前就布置给学生进行准备，实验分小组进行，一般3人一组，小组成员在课下共同搜集材料，进行建模．比如住房按揭贷款问题：某人想要购买一套价值100万元的三室一厅商品房，他自筹了40万元，要购房还需要贷款60万元，他准备办理公积金贷款，按照最新公积金贷款利率，贷款30年的年利率为4.50%，那么这个人需要具备什么偿还能力才能贷款？这就需要学生自己去查询银行贷款的各项数据，通过计算月利率，月还款额，对模型进行求解，并将模型推广，制定出个人住房公积金贷款万元还本息金额表．由于大学生毕业后的头等大事就是购房，因此通过研究这一问题可以使学生更加体会到数学的应用价值．

（3）归纳总结，深化教学目标．

指导学生归纳总结，撰写建模论文．建模论文是学生对建模过程的浓缩和记录，是用数学语言表述问题解决过程的基本形式，通过建模论文的撰写，加深对数学知识的认识和理解，深化教学目标．数学建模实验是一个从实际到数学，再从数学到实际的过程，在学生发现问题、分析问题、解决问题的整个过程中，是对学生进行的一种全面的科研实践和训练活动，在提高学生的综合应用和分析能力、语言表达和科技论文写作能力、洞察力、想象力、团结协作和创新精神等方面都起了一定的作用．

4 数学实验的评价

数学实验内容是开放的，学生可以做老师布置的数学实验任务，也可以进行扩展和探究，因此数学实验成绩的评定应更具有开放性和灵活性．教师将学生成绩分上机实验成绩、实验报告成绩和建模论文成绩3方面进行评定．

学生成绩=上机实验成绩×30%＋实验报告平均成绩× 30%＋建模论文平均成绩×40%．

（1）上机实验成绩．

基础实验主要学习Mathematica软件的应用，在学期结束时进行上机考试，要求学生在2课时的时间内将所学过的命令自拟题目进行运用并提交．

（2）实验报告成绩．

基础实验要求学生上交实验报告，根据基础实验的目的，制定了实验报告评分标准，要求学生每次上机实验后写出数学实验报告．数学实验报告评分标准如表2：

表2 数学实验报告评分标准

（3）建模论文成绩．

建模实验要求按照建模论文格式提交建模论文，建模论文评分标准如表3：

表3 建模论文评分标准

撰写建模论文虽然难度较大，但是可以通过小组合作完成，每个学生都能发挥自己的特长，如搜集信息、计算、分析、写作等．这种评价其实也包含了对学生的分工合作能力、团结协作精神等情感因素的评价[12]．

5 数学实验的教学效果

（1）提高了学生的数学学习兴趣，加深了对数学知识的理解．

数学实验课的开设为潍坊学院数学教学改革带来了生机和活力，不仅使学生体会到了数学的应用价值，同时也提高了学生学习数学的兴趣，加深了对数学知识的理解．很多学生谈到了数学实验给他们数学学习带来的惊喜：“原来对数学不感兴趣，一看数学计算就头疼，没想到数学实验能用计算机学数学，原来费半天劲用那么多技巧才能算出来的极限、导数、积分等问题，现在用Mathematica一下就算出来了，真是太神奇了！并且用它解决了很多实际生活中的问题，是数学实验使我们重新认识了数学！”

（2）数学建模活动广泛开展．

数学实验课程的开设使学生更多地了解到数学建模的知识，为此学校还开设了数学建模实训课程选修课和组建了数学建模协会，得到了学生们的积极响应，为数学建模爱好者提供了一个展示才华的舞台，激发了他们的创造力、创新力，加强了他们的实践应用能力，培养了他们的团队精神和拼搏精神，带动了他们参加“全国大学生数学建模竞赛”的热情，为大学生科技创新活动开阔了新天地[13]．

6 总 结

在高等数学课程中开设数学实验教学的研究为广大数学教育工作者提供了新的视角，事实证明数学实验教学是学生应用数学解决实际问题的最佳途径，是数学教育的自身目标和社会目标的最完美结合；是培养创新型、应用型和复合型人才的最佳载体[14]．数学实验开展以来为高等数学课程带来了活力，提高了学生学习数学的兴趣，加深了对数学知识的理解，深化了数学知识的应用，同时数学实验课程的开设使学生们更多地了解到数学建模的知识．数学建模活动作为一项科技创新活动，受到了学生们的积极响应，为数学建模爱好者提供了一个展示才华的舞台，激发了他们的创新力、加强了他们的实践应用能力、培养了他们的团队精神和拼搏精神，带动了大学生参加“全国大学生数学建模竞赛”的热情，为大学生科技创新活动开阔了新天地．

虽然数学实验在高等数学教育中所起的作用及价值已得到证实，但是数学实验课如何体现“工学结合”，如何将数学知识与专业知识进一步融合还有待于研究．随着教育教学改革的深入发展，相信这门创新性的课程一定会在培养和造就各类专门人才中发挥更大的作用．

[1] 郭迎春．实验与教学相结合改革高等数学教育模式[J]．数学教育学报，2008，17（3）：76-77．

[2] 曾宪林，李明振．高校数学建模方法的教学策略研究[J]．数学教育学报，2012，21（6）：88-90．

[3] 刘丽颖，黄翔．美国数学教材中的“动手做”[J]．数学教育学报，2005，14（2）：53-55．

[4] 曹一鸣．数学实验教学模式探究[J]．课程·教材·教法，2003，（1）：46-48．

[5] 周玮．融数学实验于高职数学教学的实践与研究[J]．数学教育学报，2010，19（6）：79-81．

[6] 彭涓，王庆岭．高等数学实用教程[M]．北京：北京师范大学出版社，2010．

[7] 周玮．高等数学（工科类）[M]．北京：北京师范大学出版社，2011．

[8] 尚春虹．数学实验教学的探索与实践[J]．数学教育学报，2002，11（3）：66-68．

[9] 王高峡，唐瑞芬．再谈美国的微积分教学改革[J]．数学教育学报，2000，9（4）：70-72．

[10] 韩旭里．数值计算与数学建模结合教学的实践[J]．数学教育学报，2008，17（3）：74-75．

[11] 洪双义．一种新型数学教育方式的探索——“数学建模教学”实验小结[J]．数学教育学报，2003，12（2）：91-94．

[12] 赵建昕．提高数学建模能力的策略研究[J]．数学教育学报，2004，13（3）：50-52．

[13] 张双德，杨灿荣．大学生数学建模竞赛与高等数学教育改革[J]．数学教育学报，1999，8（3）：64-66．

[14] 王光明．高效数学教学行为的特征[J]．数学教育学报，2011，20（1）：35-38．

Exploration and Research of Developing Experiment Teaching in Higher Mathematics Course

GAO Jie1, ZHOU Wei2
(1. School of Mathematics and Information Sciences, Weifang University, Shandong Weifang 261061, China; 2. Basic Research Department, Jinan Engineering Vocational & Technical College, Shandong Jinan 250200, China)

In this paper, the connotation of developing mathematics experiment teaching in the higher mathematics course and the teaching content、teaching design、teaching implementation、evaluation method are studied. The mathematical experiment contents are designed combining with the teaching content of Higher Mathematics, the mathematics experiment is divided into basic experimental and modeling experimental, through specific examples illustrate key steps using Mathematics software for mathematical experiment, and the concrete implementation of the mathematics experiment is discussed in detail.

higher mathematics; mathematical experiment; mathematical modeling; mathematics software

G642.0

：A

：1004–9894（2015）03–0086–05

[责任编校：周学智]

2014–12–30

山东省自然科学基金项目（ZR2011AL008；ZR2012AM017）；山东省职成教“十二五”规划课题——以提高质量为重点的高职数学教学改革创新研究（2011ZCJG056）；潍坊市科技发展计划项目（201101133）

高洁（1971—），女，山东潍坊人，副教授，硕士，主要从事微分方程、数学学科教学研究．