采用仿射不变矩的谐振接地系统故障选线方法研究

许 晔，郭谋发，杨耿杰，高 伟，缪希仁

(福州大学电气工程与自动化学院，福建福州350116)

采用仿射不变矩的谐振接地系统故障选线方法研究

许 晔，郭谋发，杨耿杰，高 伟，缪希仁

(福州大学电气工程与自动化学院，福建福州350116)

对谐振接地系统单相接地故障特征的分析表明，单相接地初始阶段故障线路与健全线路间的零序电流波形相似度低于各健全线路间的零序电流波形相似度，且故障初始时刻故障线路与健全线路的零序电流极性相反，高阻接地时该结论仍成立。仿射不变矩恰能反映各零序电流波形的整体形状特征和极性关系，且不受波形平移、旋转和缩放等仿射变换的影响，抗干扰能力强。对从各故障暂态零序电流波形图中提取的仿射不变矩特征量进行谱系聚类分析，并计算聚类有效性指标，选取聚类有效性最高的聚类树实现故障选线。各种故障工况的大量仿真表明，该选线方法适应性好，可靠性高。

谐振接地系统;故障选线;仿射不变矩;聚类分析

1 引言

谐振接地系统中，消弧线圈的补偿作用虽能减小短路电流，但也给故障选线带来困难。国内外许多选线方法不断涌现。工频量选线法［1］应用历史长，但故障电流微弱易受干扰，选线效果不理想。信号注入法为主动式选线，但需附加装置且高阻接地时选线可靠性低。暂态量选线法［1-3］因暂态量所含信息丰富而受关注。利用故障初始时刻波形的极性差异的选线方法主要有首半波极性法［2］和波形相关分析法［3］。首半波法存在假设性缺陷［1］，在暂态电流振荡剧烈和干扰存在的情况下易发生极性误判。波形相关分析法抗干扰能力强，但在高阻接地时波形差异小，选线准确性有待商榷。

近年来，智能选线方法［4-6］成为主要发展趋势。文献［4］以S变换提取故障特征量，提出融合投票结果并给出信心度的故障选线新思路，但信心度只是一个可靠性度量，没有显著提高高阻接地时的选线准确性。文献［5］将EMD方法消噪后的信号输入Duffing振子系统，由所得相图进行选线，在高阻接地时仍能正确选线;但用相图选线时需人为介入。文献［6］提出暂态零序电荷-电压特征与支持向量机结合的选线方法，对各种故障工况有良好外扩能力。支持向量机仅需小样本训练，但系统状态发生大变动时的适应性有待验证。

本文从谐振接地系统暂态零序电流波形特征出发，提出一种仿射不变矩与聚类分析结合的选线方法。仿射不变矩能反映各零序电流波形的整体形状特征和极性关系，不受波形平移、旋转和缩放等仿射变换的影响，抗干扰能力强。聚类分析使选线过程无人为介入，通过有效性计算选择最佳方案，提供选线结果的置信度。聚类分析无需先验知识，能适应各种复杂配电系统，具有可移植性。经仿真验证，该方法对各种故障工况均有良好的适应性。

2 零序电流波形特征分析

谐振接地系统发生单相接地等效于在接地点接入一零序电压源，各线路等效对地电容及消弧线圈等效电感构成零序电流回路，零序等效网络如图1所示。图1中线路L1为健全线路，线路L2为故障线路;C01、C02分别为线路1和线路2的等效对地电容;R0为包含故障点接地电阻的零序回路等值电阻; u0为零序网络电源;RL、L分别为消弧线圈有功损耗等值电阻和等值电感。

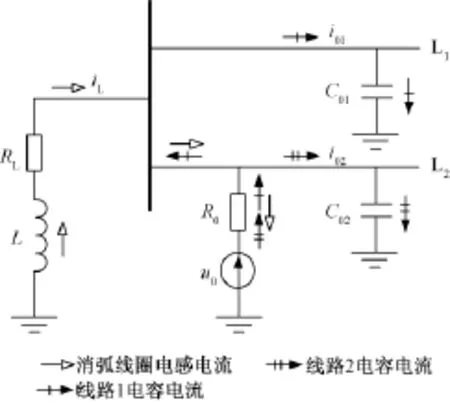
图1 单相接地故障时的零序等效网络Fig.1 Zero-sequence equivalent network of single-phase earth fault

消弧线圈通常采用过补偿方式，此时各健全线路零序电流为线路本身电容电流，故障线路零序电流为全系统各健全线路电容电流与消弧线圈电感电流之和。

通过对零序等效网络列写方程，可计算得到单相接地故障电流。健全线路和故障线路首端测得零序电流分别为:

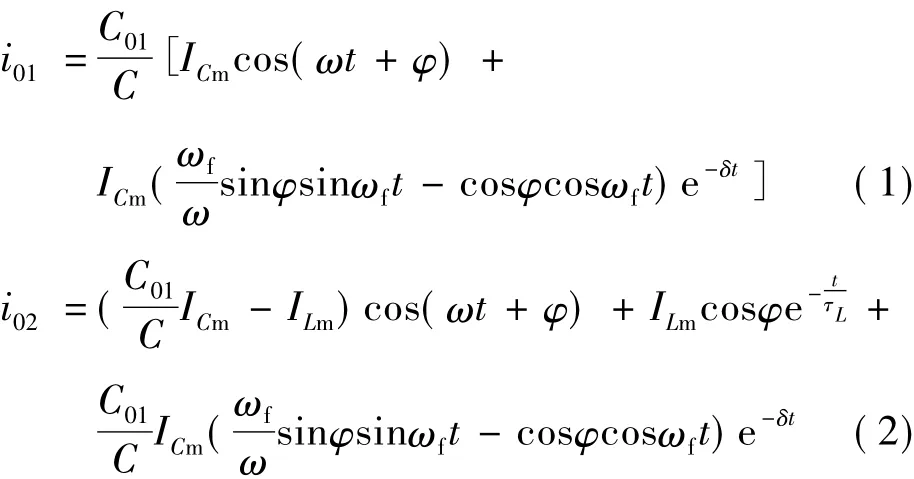
式中，C=C01+C02为全系统等效对地电容;ICm为电容电流幅值;ω为工频角频率;φ为接地瞬间电源电压的相角;ωf和δ分别为暂态自由振荡分量角频率和衰减系数;ILm为电感电流的幅值;τL为电感回路的时间常数。

由式(1)和式(2)可知，各健全线路首端流过的零序电流为线路本身电容电流，容性无功功率从母线流向线路。故障初始阶段消弧线圈电感电流不突变，未发挥补偿作用。此时故障线路首端流过的电流为各健全线路电容电流之和，容性无功功率从线路流向母线，与各健全线路的无功流向均相反。

采用MATLAB软件建立包含6条馈线的谐振接地系统仿真模型，如图2所示。其中，110kV变压器型号为SZ-31500/110，10kV配电变压器型号为S11-MR-1000/10，Z型变压器型号为JSC-200/10.5。消弧线圈过补偿度为5%。线路采用分布参数的PI型等值电路模型，电缆线路和架空线路参数如表1所示。采样频率为20kHz。

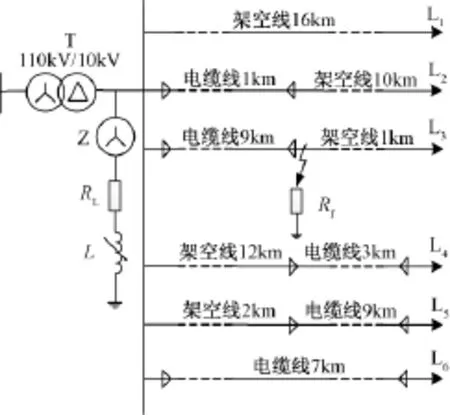
图2 仿真模型Fig.2 Simulation model

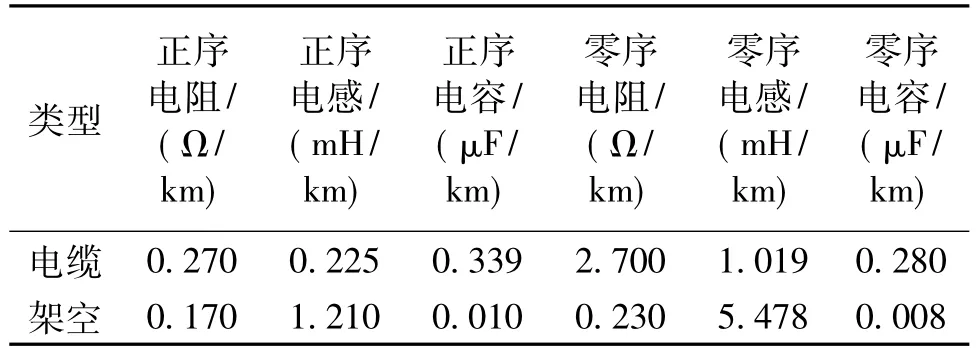
表1 电缆线路和架空线路参数Tab.1 Parameters of cable line and overhead line

图3 接地电阻为2Ω时的零序电流波形Fig.3 Zero-sequence current waveforms when ground resistance is 2Ω

线路3距离母线9km处发生B相接地故障，故障初相角为45°，接地电阻为2Ω。故障后各线路零序电流波形关系如图3所示。在故障后1/2个工频周期内，故障线路与健全线路间的零序电流波形的相似度低于各健全线路间的零序电流波形相似度，且故障初始时刻故障线路与健全线路的零序电流极性相反。

其余条件不变，接地电阻为2000Ω时，故障后线路L2、L3、L5零序电流波形如图4所示。故障后1个工频周期内，系统中的零序电流幅值缓慢上升，故障线路与健全线路间的零序电流波形的相似度低于各健全线路间的零序电流波形相似度，且故障初始时刻故障线路与健全线路的零序电流极性相反。

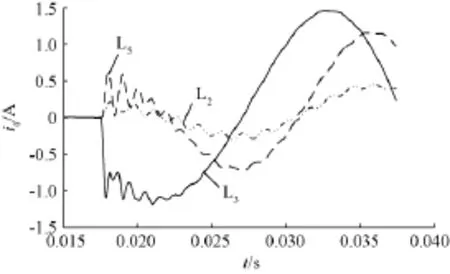
图4 接地电阻为2000Ω时的零序电流波形Fig.4 Zero-sequence current waveforms when ground resistance is 2000Ω

综上所述，故障初始阶段故障线路与健全线路间的零序电流波形的相似度低于各健全线路间的零序电流波形相似度，且故障初始时刻故障线路与健全线路的零序电流极性相反。高阻接地时该结论仍成立。该特征可用于区分故障线路与健全线路。

3 不变矩算法

不变矩算法是一种图像描绘方法，可将图像特征如幅值、边缘等以“描述子”——“矩”来表征，用于图像的识别。一个图像可求出一组具有对仿射变换(包括平移、旋转和缩放等)不变的不变矩［7］，反映图形的整体形状特征。

设离散图像的灰度分布函数为F(x，y)，则图像的p+q阶原点矩为:

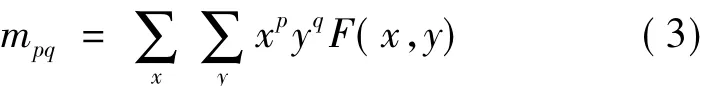
矩值mpq由灰度分布函数F(x，y)唯一确定。显然，原点矩不具备平移不变的特性。通过减去灰度重心坐标，得p+q阶中心矩:

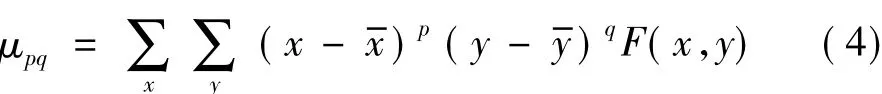
再经过归一化处理，得到归一化的p+q阶中心矩［8］:

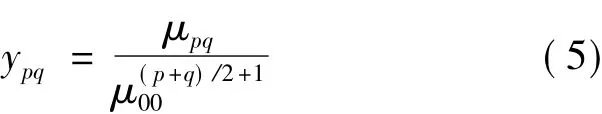
归一化的p+q阶中心矩能剔除平移变换和缩放变换的影响，具有不变的特性。现简单证明如下。

设平移变换后x'=x+α，y'=y+β，代入式(3)～式(5)可得y'pq=ypq。平移变换后，归一化的p+q阶中心矩不变。

设图像经过缩放因子为k的缩放变换，则x'= kx，y'=ky。代入式(3)～式(5)，易证明y'pq=ypq，归一化的p+q阶中心矩具有缩放不变性。

Jan Flusser用归一化的2～4阶中心矩(即p+q≤4)构造出不受平移、缩放和旋转等仿射变换影响的11个仿射不变矩［9］。其中ψ4、ψ6、ψ9、ψ11这4个不变矩如下:

仿射不变矩ψ4、ψ6、ψ9、ψ11能描述图形的极性特征，简单证明如下。

关于某一主轴的镜像变换后(以X轴为例)，x'= x，y'=－y。由式(4)可得μ'00=μ00，μ'pq=(－1)q· μpq。代入式(5)可得y'pq=(－1)qypq。当q为奇数时y'pq=－ypq，当q为偶数时y'pq=ypq。将此结论代入式(6)，可知镜像变换后，图像的4个仿射不变矩ψ4、ψ6、ψ9、ψ11的值均为原值的相反数。

因此，仿射不变矩ψ4、ψ6、ψ9、ψ11能描述零序电流波形的整体形状特征和极性关系，且具有对仿射变换(包括平移、旋转和缩放等)的不变性。下面以第2节所得的零序电流波形图验证该结论。

接地电阻为2000Ω时，取故障后1个工频周期的暂态故障电流波形。令图像灰度分布函数F(t，i)等于1，相当于形成二维的二值图像，波形上的点灰度为1，波形外的点灰度为0。计算各线路零序电流波形的仿射不变矩，结果如表2所示。

观察表2，虽然受图像灰度分布函数数值的影响，各仿射不变矩的数值较小，但能明显看出故障线路(线路3)与各健全线路的ψ4、ψ6、ψ9、ψ11这4个仿射不变矩的符号均相反，数值相差较大，而其他仿射不变矩的符号则相同。故仿射不变矩ψ4、ψ6、ψ9、ψ11可用于表征故障线路与各健全线路的零序电流波形的整体形状特征和故障初始时刻的极性关系。因此，可利用各故障暂态零序电流波形图的仿射不变矩特征值ψ4、ψ6、ψ9、ψ11来区分故障线路与健全线路。

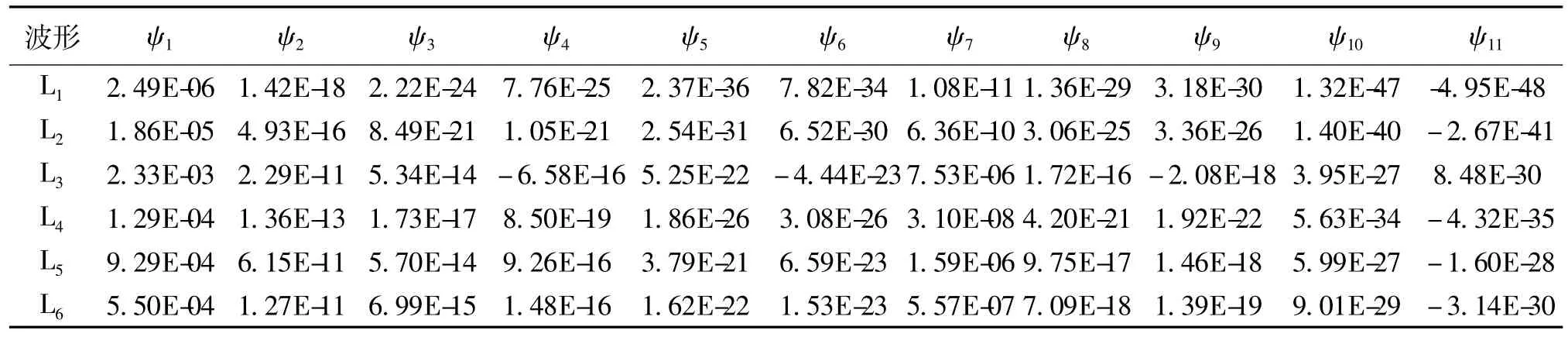
表2 典型故障暂态零序电流波形的仿射不变矩计算结果Tab.2 Affine moment invariants calculation of transient zero-sequence current waves in typical fault

4 聚类分析

实际谐振接地系统中，各线路长度和类型的不同导致故障初始阶段各暂态零序电流的仿射不变矩特征值发生变化，人为设定阈值的选线方法适应性差，因此对提取的仿射不变矩特征量进行聚类分析，使选线过程无人为介入，增强算法适应性。

样本间距离测度和类间距离测度是聚类分析的基础，测度描述了对象的差异性和相似性。下面依次介绍样本间距离测度和类间距离测度。

在聚类分析中最常用的样本间距离测度是欧氏距离。设两个样本的n维观测数据分别为xi=(xi1，xi2，…，xin)和xj=(xj1，xj2，…，xjn)，则样本间欧氏距离为:

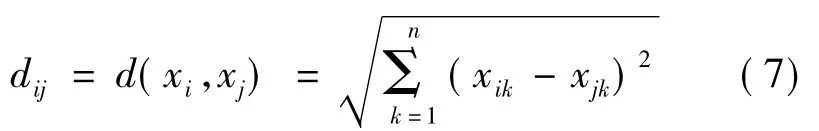
设Gs和Gt为分别含有ns和nt个样品的两个类别，类间距离测度通常有以下5种:

(1)最短距离:两个类别中样本间距离的最小值作为类间距离测度。

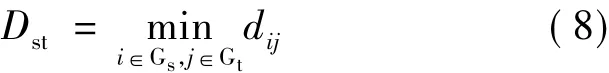
(2)最长距离:两个类别中样本间距离的最大值作为类间距离测度。

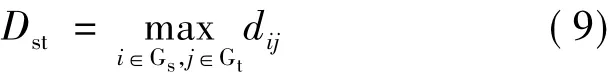
(3)类平均距离:两个类别中所有样本两两距离的平均。其优点是充分利用类中各样本所含信息。

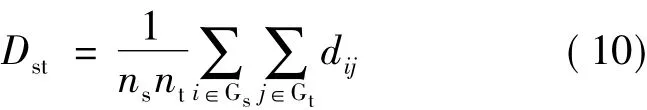
(4)重心距离:两个类别的重心间的欧式距离称为重心距离。

(5)离差平方和距离:正比于重心距离。

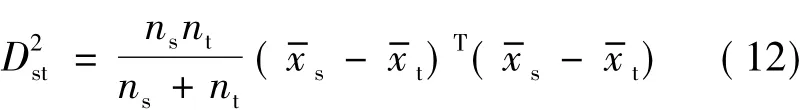
本文采用谱系聚类法进行聚类分析，谱系聚类法是一种较常用的静态聚类法。其基本思想是所有线路首先各自成类，然后聚合特征量距离最近的两类，计算新的类间距离，再进行聚合处理。如此往复，逐次聚合特征量距离最近的两类，直至所有线路聚为一类。谱系聚类无需先验知识，对初始条件不敏感。

不同的距离测度与聚类算法搭配，聚类结果将呈现不同程度的差异。为衡量聚类有效性引入谱系聚类有效性指标——cophenet相关系数［10］。cophenet相关系数为聚类树的类间距离与所有样本间的原始距离的相关关系。设Yij为样本i和样本j的原始距离，为原始距离的平均值;Zij为样本i和样本j在聚类树中的距离，为聚类树类间距离的平均值，则cophenet相关系数为:

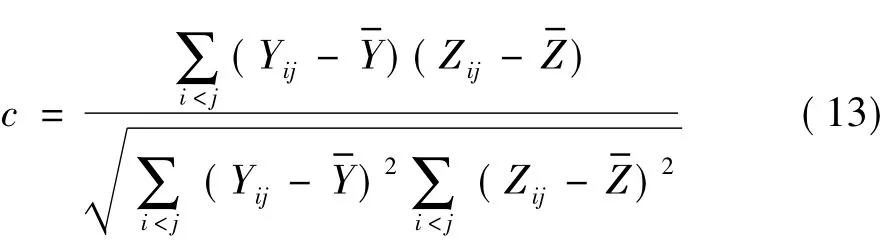
以表2所得特征量为例，将表征零序电流波形的整体形状特征和极性关系的4个仿射不变矩特征量ψ4、ψ6、ψ9、ψ11，以最短距离、最长距离、类平均距离、重心距离和离差平方和距离等5种类间距离分别进行谱系聚类分析，并计算各聚类方案的cophenet相关系数，如表3所示。5种方案的相关系数均高于0.94，说明谱系聚类算法能有效地判别故障线路和健全线路。5种方案中，以类平均距离和以重心距离进行谱系聚类的方案cophenet相关系数最高，聚类效果最好。因此选取聚类有效性最高的方案3和方案4进行谱系聚类分析。

表3 各聚类方案的cophenet相关系数Tab.3 Cophenetic correlation coefficient of each clustering scheme

画出cophenet相关系数最高方案(方案3、方案4)和最低方案(方案5)的谱系聚类图，如图5所示。图5中，cophenet相关系数最高的方案3和方案4聚类树相差无几，这由二者cophenet相关系数相等和式(13)亦可推知。聚类树进一步印证了以cophenet相关系数最高的方案进行谱系聚类时，故障线路与健全线路差异性更大，更有利于故障选线。

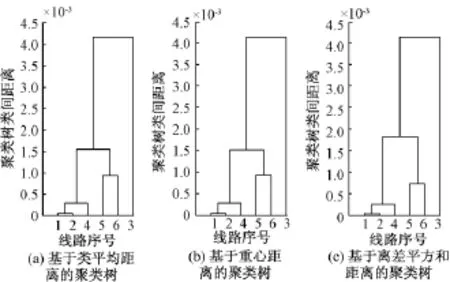
图5 谱系聚类图Fig.5 Pedigree clustering figure

用方案3和方案4的谱系聚类树分别进行故障选线，将线路分为故障线路和健全线路两类，最终聚类结果如表4所示。谱系聚类分析能准确地将故障线路(即线路3)单独划分为一类。

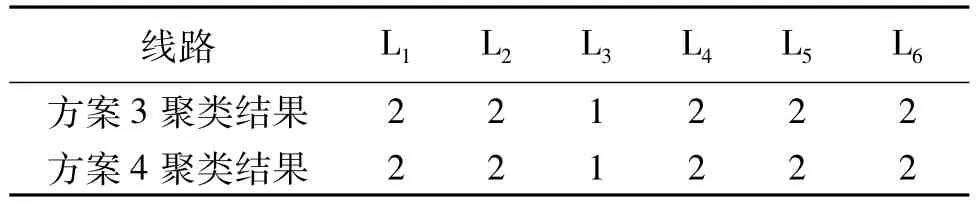
表4 谱系聚类结果Tab.4 Pedigree clustering result

5 选线方法

在仿射不变矩和谱系聚类原理分析的基础上，给出谐振接地系统故障选线算法流程，如图6所示。

图6 选线方法流程图Fig.6 Flow chart of fault line detection

取故障后1个工频周期内各线路首端测得的零序电流;令电流波形曲线上的点灰度为1，其余为零，得到图像灰度分布函数F(t，i)，进而求取反映波形形状特征的11个仿射不变矩;提取其中4个仿射不变矩特征量 ψ4、ψ6、ψ9、ψ11，分别以最短距离、最长距离、类平均距离、重心距离和离差平方和距离5种类间距离进行谱系聚类分析，并计算5种聚类方案的cophenet相关系数。选取cophenet相关系数最高的聚类方案(即聚类效果最佳的聚类树)进行故障选线。

6 仿真验证

采用图2仿真模型，对单相接地故障发生在不同线路、不同故障位置、不同故障初相角、不同故障电阻等情况进行仿真分析，验证了线路末端故障、高阻接地故障、采样不同步、电磁噪声干扰和不同补偿度等故障选线恶劣工况下的算法适应性。

6.1 典型故障

挖泥船从海侧向陆侧方向进行开挖，前后各布2门八字锚。然后根据测量导航软件窗口中自动实时动态显示的当时船位指挥抓泥船定位，挖泥船就位后即可停靠驳准备开挖。由8m3抓斗式挖泥船开挖，分层按等于2m控制。

对发生在不同工况下的单相接地故障进行仿真，随机抽取6组选线结果，如表5所示。选线结果表明，在各种故障工况下，采用仿射不变矩的选线方法均能准确选线。

表5 典型故障选线结果Tab.5 Results of fault line detection in typical fault

6.2 线路末端故障

线路末端发生单相接地故障时，因故障电流较小，故障特征微弱，易受干扰导致错误选线。为验证本文所提出方法的选线效果，现仿真不同故障初相角和不同接地电阻情况下各馈线末端发生单相接地故障，随机抽取6组选线结果，如表6所示。

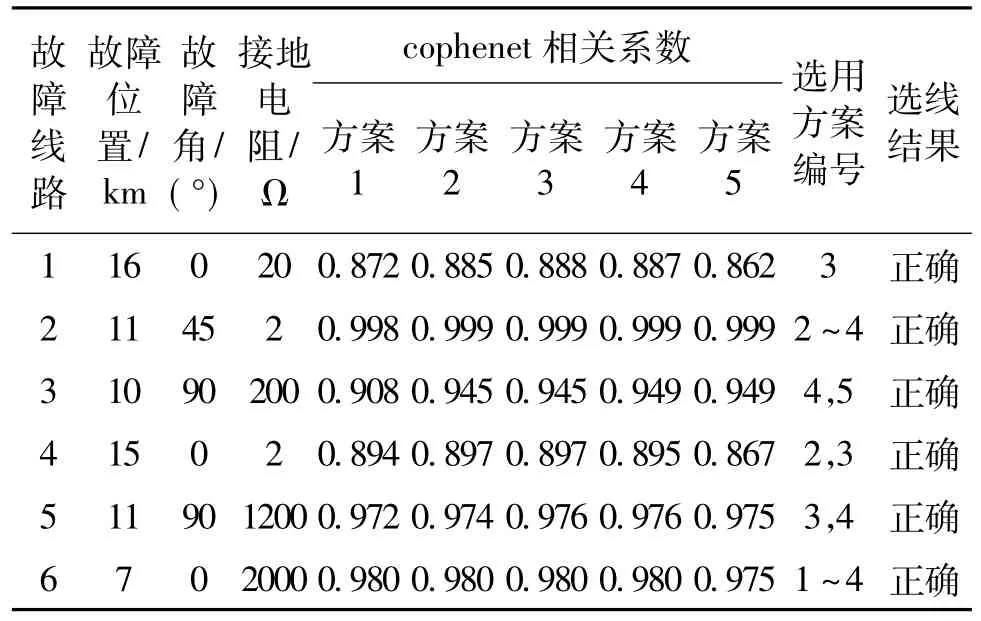
表6 线路末端故障选线结果Tab.6 Fault line selection results with line-end fault

针对线路末端故障的情况，本文提出的选线方法能够准确地辨识故障线路。

6.3 高阻接地故障

考虑高阻接地同样存在故障特征微弱使选线困难的问题，仿真不同故障条件下各馈线发生高阻接地(2000Ω)故障。随机抽取6组选线结果，如表7所示。本文提出的选线方法对高阻接地这种恶劣工况下的故障具有良好的辨识能力。

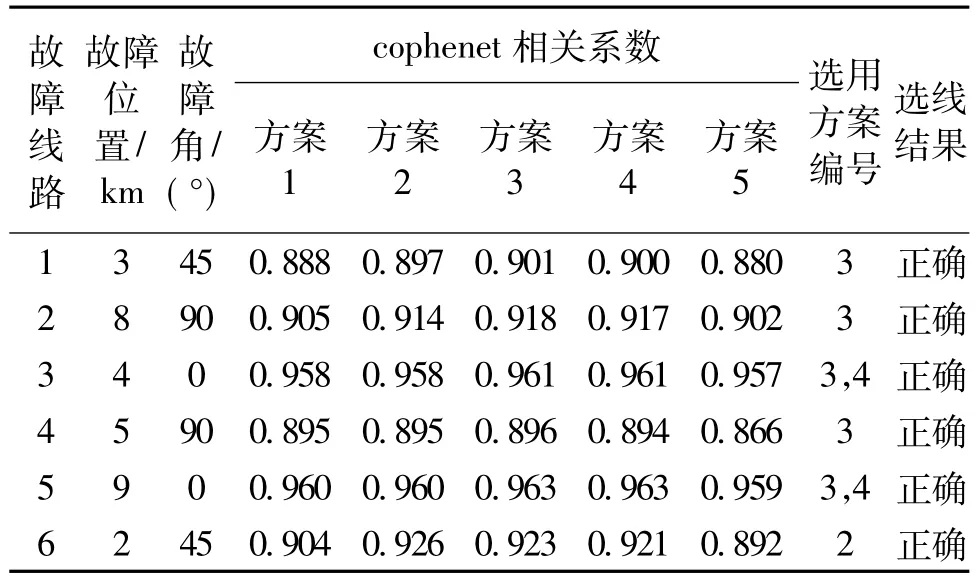
表7 高阻接地故障选线结果Tab.7 Results of fault line detection with high resistance

6.4 采样不同步

采样信号不同步的问题普遍存在于实际系统中。这使采样所得信号间存在一定的相位误差，给准确选线带来困难。在线路末端高阻接地且故障初相角为零(电压为零)等故障选线恶劣工况并存条件下，仿真验证该选线方法对采样不同步的适应性。以线路1的原始电流信号为基准分别滞后10个、15个和 20个采样点，即滞后时间分别为 0.5ms、0.75ms和1ms，结果如表8所示。

表8 采样不同步的选线结果Tab.8 Results of fault line detection with asynchronous sampling

理论分析中，仿射不变矩特征量具有平移不变的特性，因此能克服采样不同步带来的不利影响。仿真结果与理论分析一致，证明该方法对采样不同步具有良好的适应性。

6.5 电磁噪声

实际采集的电量信号中包含高频噪声，影响选线准确性。在仿真线路末端高阻接地且故障初相角为零等恶劣故障工况并存情况下，对电量信号加高斯白噪声干扰，验证该方法对噪声干扰的适应性，结果如表9所示。

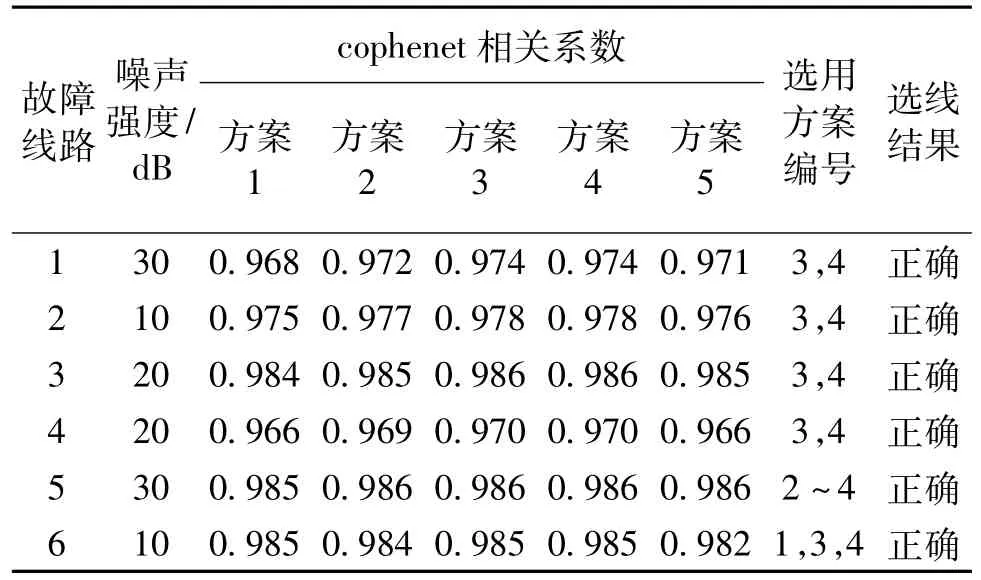
表9 噪声干扰下的选线结果Tab.9 Results of fault line detection with noise

仿真结果表明，在电磁噪声干扰下，该选线方法仍能准确辨识故障线路。侧面说明仿射不变矩数值小不影响计算结果的抗干扰性。理论分析上看，一定程度的电磁干扰并不影响各暂态零序电流波形的整体形状特征和极性关系。验证结果与理论分析相一致。

6.6 不同补偿度

消弧线圈补偿度直接影响暂态零序电流幅值，进而影响选线结果。下面以线路3为例，仿真线路末端高阻接地且故障初相角为零等恶劣故障工况并存情况下，对补偿度分别为5%和8%的系统验证该选线方法的适应性，如表10所示。

表10 不同补偿度系统的选线结果Tab.10 Results of fault line detection in different compensation types

仿真结果表明，该方法能适应不同补偿度系统。

7 结论

本文提出了一种采用仿射不变矩特征量进行谱系聚类分析以实现配电网谐振接地系统故障选线的方法。理论分析和仿真验证可得出以下结论:

(1)故障初始阶段故障线路与健全线路间的零序电流波形的相似度低于各健全线路间的零序电流波形相似度，且故障初始时刻故障线路与健全线路的零序电流极性相反。

(2)对各暂态零序电流波形图求取描述波形整体形状特征和极性关系的4个仿射不变矩，进行谱系聚类分析，选取聚类有效性最高的聚类树进行故障选线。该过程无需先验知识，对初始条件不敏感。

(3)大量仿真表明，该方法在线路末端高阻接地的恶劣故障工况下仍能正确选线，对采样不同步、电磁噪声和不同补偿度等情况均有良好的适应性，能克服首半波极性法和波形相关分析法存在的缺陷，适应工程应用中可能存在的各种影响因素，准确辨识故障线路。

［1］束洪春(Shu Hongchun).配电网络故障选线 (Fault line selection of distribution power system)［M］.北京:机械工业出版社 (Beijing:China Machine Press)，2008.

［2］胡佐，李欣然，石吉银 (Hu Zuo，Li Xinran，Shi Jiyin).基于残流与首半波综合的接地选线方法研究(Analysis of earth fault selection based residual current and current angle integration)［J］.继电器 (Relay)，2006，34(7):6-9.

［3］毛鹏，段玉倩，姜娜 (Mao Peng，Duan Yuqian，Jiang Na).基于相关分析的故障选线方法 (A correlation analysis based method to detect faulty line under single phase to ground fault occurred in distribution network with small current neutral grounding)［J］.电网技术 (Power Systems Technology)，2004，28(2):36-39.

［4］张钧，何正友，贾勇 (Zhang Jun，He Zhengyou，Jia Yong).基于S变换的故障选线新方法 (Fault line identification approach based on S-transform)［J］.中国电机工程学报 (Proceedings of the CSEE)，2011，31 (10):109-115.

［5］张淑清，翟欣沛，董璇，等(Zhang Shuqing，Zhai Xinpei，Dong Xuan，et al.).EMD及Duffing振子在小电流系统故障选线方法中的应用 (Application of EMD and Duffing oscillator to fault line detection in un-effectively grounded system)［J］.中国电机工程学报 (Proceedings of the CSEE)，2013，33(10):161-167.

［6］张姝，何正友，王玘，等 (Zhang Shu，He Zhengyou，Wang Qi，et al.).暂态零序电荷-电压特征与支持向量机结合的谐振接地系统故障选线研究 (Fault line selection of resonant grounding system based on the characteristics of charge-voltage in the transient zero sequenceand support vector machine)［J］.电力系统保护与控制 (Power System Protection and Control)，2013，41 (12):71-78.

［7］曹健 (Cao Jian).图像目标的表示与识别 (Representation and recognition of the image target)［M］.北京:机械工业出版社(Beijing:China Machine Press)，2012.

［8］Hu M K.Visual pattern recognition by moment invariants［J］.IRE Transactions on Information Theory，1962，8 (2):179-187.

［9］Flusser J.On the independence of rotation moment invariants［J］.Pattern Recognition，2000，33(9):1405-1410.

［10］李柏年，吴礼斌 (Li Bonian，Wu Libin).MATLAB数据分析方法 (Matlab data analysis methods)［M］.北京:机械工业出版社(Beijing:China Machine Press)，2011.

New approach to detect fault line in resonant earthed system using affine moment invariants

XU Ye，GUO Mou-fa，YANG Geng-jie，GAO Wei，MIAO Xi-ren
(College of Electrical Engineering and Automation，Fuzhou University，Fuzhou 350116，China)

The analysis of the characteristic of neutral point resonant earthed system with single-phase-to-ground fault is made.The result shows that the similarities of zero sequence current waveforms between the fault line and each healthy line are below those between healthy lines，and zero sequence current of the fault line is in opposite polarity as those of healthy lines in initial stage of single-phase-to-ground fault.This situation remains during high resistance grounded fault.Affine moment invariants can just reflect the overall shape and polarity of each zero sequence current without influence from affine transformation(such as rotation，translation and scale)，and has a strong anti-jamming capability.The fault line is detected according to the pedigree clustering analysis of affine moment invariants which is extracted from transient zero-sequence current waveforms of each line.Substantial simulations are conducted among various kinds of fault conditions.The results in various fault conditions show that the method is flexible and reliable.

resonant earthed system;fault line detection;affine moment invariants;clustering analysis

TM 862

:A

:1003-3076(2015)07-0037-08

2013-12-07

国家自然科学基金资助项目(51377023)

许 晔(1989-)，女，福建籍，硕士研究生，研究方向为配电网自动化;郭谋发(1974-)，男，福建籍，副教授，硕士，研究方向为电力系统自动化(通讯作者)。