基于改进人工蜂群算法的输电网扩展规划

周智成，童买成，徐璐，蔡婷

(1.广西电网电力调度控制中心，广西 南宁 530023；2.广西电网柳州供电局，广西 柳州 545005；3.广西电网防城港供电局，广西 防城港 538001)

基于改进人工蜂群算法的输电网扩展规划

周智成1，童买成2，徐璐3，蔡婷2

(1.广西电网电力调度控制中心，广西 南宁 530023；2.广西电网柳州供电局，广西 柳州 545005；3.广西电网防城港供电局，广西 防城港 538001)

针对标准人工蜂群算法存在计算精度不高、容易陷入局部最优和迭代后期速度慢等缺点，对算法提出四点改进：(1)引领蜂阶段引入差分变异算子和交叉算子更新蜜源位置，并用退火选择策略接受新蜜源；(2)选择阶段采用锦标赛选择策略计算蜜源被跟随蜂选择的概率；(3) 跟随蜂阶段引入学习因子更新蜜源位置，并用退火选择策略接受新蜜源；(4)增加对当前最优蜜源的混沌局部搜索。改进的算法提高了全局和局部搜索能力，有效避免算法过早陷入局部最优。建立以年新建费用与年网损费用之和最小的输电网规划模型，以Garver-6节点系统和Garver-18节点系统为例，验证改进人工蜂群算法应用于输电网规划中的有效性。

输电网规划；人工蜂群算法；差分算法；混沌搜索

1 引言

输电网规划是电力系统规划的重要组成部分，它在电源规划、变电站规划和负荷预测的基础上，规划在何时、何地新建何种类型的输电线路。目前对输电网规划研究主要集中在数学模型的建立和求解方法上。随着输电网规划复杂性的增加，传统的输电网规划方法并不能完全满足现代输电网规划的要求，智能优化算法为输电网规划模型的求解提供了一条新的途径。目前，遗传算法、粒子群算法、蚁群算法、人工鱼群算法和差分进化算法等智能优化方法已成功应用于输电网规划中。

2005年，土耳其学者Dervis Karaboga根据蜂群的高效开采蜜源的方式，首次提出了人工蜂群算法[1](Artificial Bee Colony algorithm，ABC)，它是一种新型的智能优化算法。由于ABC算法具有灵活性大、鲁棒性好、参数设置少和易与其他算法结合等优点，已经在电力系统的许多领域得到广泛的应用[2-4]。本文针对ABC算法存在收敛精度不高、容易陷入局部最优和迭代后期速度慢等缺点[5]，对算法提出四点改进措施，并尝试将改进人工蜂群算法(Improved Artificial Bee Colony algorithm，IABC)应用于输电网规划中。

2 输电网规划模型

建立以年新建费用与年网损费用之和最小的输电网规划模型，目标函数和约束条件如式(1)、式(2)所示。

(1)

s.t.

(2)

目标函数式(1)中，第一项为网络的年新建费用；第二项为为网络的年网损费用；ρ为资金返回系数，ρ=i(1+i)n/((1+i)n-1)，其中i是资金贴现率，n为支付年限；mL1为所有新建支路集合；kq、xq和Lq分别为支路q的单位长度造价、新建的回路数和可架线路的长度；mL2为网络中所有支路集合；dh为支路h的年网损费用系数，dh=Ccost*τh/u2，其中Ccost是网损电价，τh为支路h最大负荷损耗时间，u是系统额定电压；rh为支路h的电阻；Ph为支路h输送的有功功率。

约束条件式(2)中，P为节点注入的有功向量；B和θ分别为正常运行方式下网络的节点电纳矩阵和节点电压相角列向量；Bh和θh分别是正常运行方式下支路h的电纳和两端电压相角差；Phmax为支路h传输的最大功率；xqmax为支路q可新建线路的最大值；Z为整数集合。

3 人工蜂群算法

人工蜂群算法在求解具体的优化问题时，主要包括初始化阶段、引领蜂阶段、选择阶段、跟随蜂阶段和侦察蜂阶段。

(1)初始化阶段。由式(3)随机生成SN个D维的蜜源位置Xi(i=1,2,…,SN)。

(3)

(2)引领蜂阶段。采用式(4)来更新蜜源位置。

vij=xij+R(xij-xkj)

(4)

式中，j和k随机选取的值，并且k≠i。vij是Vi的第j维；R是[-1,1]范围内的随机数。比较Vi和Xi的适应度值，保留适应度值好的蜜源。

(3)选择阶段。由式(5)来计算第i个蜜源被跟随蜂选中的概率Pi。

(5)

式中，fiti是第i个蜜源的适应度值。

(4)跟随蜂阶段。跟随蜂对选择的蜜源进行一次领域搜索，即按式(4)更新蜜源位置，比较新旧蜜源的适应度值，保留适应度值较优的蜜源。

(5)侦察蜂阶段。一个蜜源位置如果经过limit次迭代后依然没有更新，采用式(3)随机生成一个新蜜源位置来代替该蜜源位置。如果没有达到结束迭代的条件，则返回引领蜂阶段。

4 改进人工蜂群算法

为了提高标准人工蜂群算法的性能，从四个方面对标准算法进行改进，下面将进行详细介绍。

(1)引领蜂阶段的改进。在标准人工蜂群算法的引领蜂阶段中，每次蜜源位置的更新仅在一个维度进行，使得蜜源进化速度缓慢，蜜源的多样性下降，算法容易陷入早熟。为了改变这种不利因素，本文引入差分变异算子和交叉算子对蜜源位置进行更新，有效提高了搜索的空间；并用退火选择策略接受新蜜源，提高了蜜源种类的多样性。差分变异算子和交叉算子分别如式(6)和式(7)所示。

(6)

(7)

(8)

式中，k为Boltzmann 常数；Tt为第t次迭代的下降温度，Tt=0.99*Tt-1。

(2) 选择阶段的改进。标准人工蜂群算法采用轮盘赌法来计算蜜源被选择的概率，这种方法在迭代的后期，很难选出优秀的蜜源，从而使蜜源进化停止，而采用锦标赛选择策略[6]计算蜜源被跟随蜂选择的概率时，由于这种的选择方式，与适应值大小不直接成比例，在一定程度上避免了算法过早停滞。

(3) 跟随蜂阶段的改进。为了加快跟随蜂阶段的局部搜索，引入学习因子F1和F2对蜜源位置进行更新，即引领蜂阶段由式(9)来更新蜜源位置。

(9)

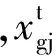
(4) 跟随蜂阶段结束后，为了提高当前最优蜜源的质量，使算法能够跳出局部最优，采用基于Tent映射的混沌系统产生混沌向量，利用混沌向量具有随机性、规律性和遍历性的优点，对当前最优蜜源进行混沌局部搜索。混沌局部搜索步骤如下：

①设混沌最大搜索次数为M，Tent映射的初始向量CH0，混沌搜索次数k=1。

(10)

式中，j=1,2,…,D。

④利用式(11)将新混沌向量ZHk与当前最优蜜源位置Xg线性组合得到一个新蜜源位置Vk。

Vk=(1-λ)Xg+λZHk

(11)

式中，收缩因子λ=e-2*t/G。进化的初期λ大。可在一个大范围内进行全局遍历搜索，有利于保持蜜源的多样性；随着迭代的增加，λ逐渐变小，有利于全局最优蜜源的精细搜索。

⑤如果Vk的适应度值优于Xg，则Vk替换Xg，同时混沌搜索结束；如果k大于M，混沌搜索也结束；否则返回步骤②，且k=k+1。

5 改进人工蜂群算法在输电网规划中的应用

5.1 构造适应度函数

适应度函数既要体现输电网规划的目标，又要满足规划方案的约束条件，即各线路在正常运行方式下没有过负荷，且输电网络没有解列现象。基于这样的考虑，适应度函数如式(12)所示。

F=

(12)

式中：γ为过负荷惩罚因子；W为网络不连通时一个较大的惩罚值；其余字母与式(1)、式(2)相同。

5.2 规划步骤

基于改进人工蜂群算法的输电网规划步骤如下：

(1) 输入输电网规划所需要的数据，设置蜜源总数、最大迭代次数和控制参数limit等；由式(3)随机生成SN个的蜜源位置。

(2)按照式(6)、式(7)更新蜜源位置，根据式(12)计算蜜源的适应度值,由式(8)计算的概率来接受新蜜源。

(3)采用锦标赛选择策略来计算新蜜源被跟随蜂选择的概率。

(4)按照式(9)更新蜜源位置，根据式(12)计算蜜源的适应度值,由式(8)计算的概率来接受新蜜源。

(5)对当前最优蜜源进行混沌局部搜索。

(6)如果一个蜜源经过limit次迭代依然没有更新，由式(3)随机生成一个新蜜源位置代替停止更新的蜜源位置。

(7)如果达到最大迭代次数，则结束程序，输出最优规划方案；否则更新参数，同时转到步骤(2)。

6 算例分析

(1)算例1

对Garver-6节点系统进行规划，Garver-6节点系统的网络结构和相关参数详见文献[7]。根据参考文献[8,9]，设线路单位长度造价为50万元·km-1，网损电价Ccost为0.3元·(kW·h)-1，线路年最大负荷损耗时间为2000h，资金贴现率i为10%，支付年限n为15年。蜜源总数为100，控制参数limit=4，混沌最大搜索次数M=20。实验环境：处理器为AMD Athlon(tm) II X2 260 ，主频3.22GHz，内存4GB的计算机。

IABC算法、ABC算法与文献[9]的标准粒子群算法(Standard Particle Swarm Optimization，SPSO)的规划结果和收敛曲线分别如表1和图1所示。

表1 Garver-6节点系统规划的结果

注：表中新建线路表达式为：节点i-节点j(新建线路值)。

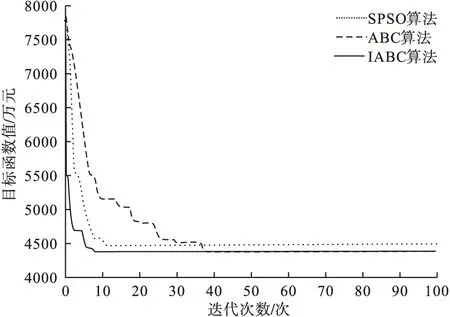
图1 Garver-6节点系统规划的收敛曲线

由表1可知，IABC算法和ABC算法的规划结果与文献[8]相同。

由图1可知，SPSO算法经过11次迭代就陷入局部最优。ABC算法和IABC算法能收敛到全局最优解，而且后者的收敛速度明显比前者快。

将ABC算法和IABC算法分别连续运行30次，收敛结果如表2所示。

由表2可知，IABC算法的稳定性和收敛速度均优于ABC算法。

表2 收敛性能比较(算例1)

(2)算例2

对Garver-18节点系统进行规划，其网络结构和相关参数详见文献[10]和算例1。蜜源总数为300，控制参数limit=4，M=20。实验环境与算例1相同。

IABC算法、ABC算法与文献[9]的SPSO算法的规划结果和收敛曲线如表3和图2所示。

表3 Garver-18节点系统规划的结果

注：表中新建线路表达式为：节点i—节点j(新建线路值)。

图2 Garver-18节点系统规划的收敛曲线

由表3可知，IABC算法和ABC算法的规划结果与文献[8]相同。

从图2可知，SPSO算法经过21次迭代后就陷入局部最优。ABC算法的收敛轨迹呈阶梯状，迭代过程中有三次陷入局部最优；而IABC算法的收敛轨迹斜率很大，整个迭代过程没有过多的重复搜索，能快速收敛到全局最优解。

将ABC算法和IABC算法分别连续运行30次，收敛结果如表4所示。

表4 收敛性能比较(算例2)

表4可知，在参数设置相同的情况下，随着规划问题的维度增加，ABC算法在30次的测试中仅有13次收敛到全局最优解。IABC算法在30次测试中能全部收敛到最优解，且收敛速度比ABC算法快。可见，在求解高维非线性规划问题中，IABC算法优于ABC算法。

7 结论

本文针对ABC算法的不足之处，从四个方面进行了分析，并提出四点改进措施。改进的算法加快了全局收敛速度，同时有效避免算法过早陷入局部最优。采用IABC算法、ABC算法和SPSO算法对Garver 6 节点系统和Garver 18 节点系统进行规划，结果表明IABC算法在收敛速度、稳定性和跳出局部最优等方面都优于ABC算法和SPSO算法，验证了IABC算法应用于输电网规划中的有效性和可行性。

[1] Karaboga D.An idea based on honey bee swarm for numerical optimization[M].Kayseri:Ericiyes University，2005:70-71.

[2] 周文越,吕飞鹏,廖小君.基于人工蜂群算法的环网方向保护配合最小断点集计算[J].电力系统保护与控制，2013,41(6):77-81.

[3] 赵志，黄文杰.改进人工蜂群算法及在风电场群调度中的应用[J].中南大学学报(自然科学版)，2011,42(10):3101-3104.

[4] 任新新，周玲，赵峰，等.基于人工蜂群算法的配电网无功优化[J].现代电力，2012,29(4):41-45.

[5] 毕晓君，王艳娇.改进人工蜂群算法[J].哈尔滨工程大学学报，2012，33(1)：117-123.

[6] 暴励.不同选择策略的人工蜂群算法分析[J].工业控制计算机，2013，26(8)：57-59.

[7] 孙洪波.电力网络规划[M].重庆:重庆大学出版社,1996.

[8] 李如琦，王宗耀，谢林峰，等.种群优化人工鱼群算法在输电网扩展规划的应用[J].电力系统保护与控制，2010,38(23):11-15.

[9] 周媛媛.改进粒子群算法在输电网络扩展规划中的应用研究[D].广西：广西大学，2009.

[10] 程浩忠,张焰,严正.电力系统规划[M].北京:中国电力出版社,2008.

Transmission Network Rxpansion Planning Based on Improved Artificial Bee Colony Algorithm

ZHOUZhi-cheng1,TONGMai-cheng2,XULu3,CAITing2

(1.Power Dispatch Control Center,Guangxi Power Grid,Nanning 530023,China;2.Liuzhou Power Supply Bureau,Guangxi Power Grid,Liuzhou 545005,China;3.Fangchenggang Power Supply Bureau,Guangxi Power Grid,Fangchenggang 538001,China)

In view of the shortcomings of standard artificial bee colony algorithm,including low calculating accuracy,being ease to fall into local optimum and computing slowly in the later optimization stage，the paper proposeds four strategies to improve algorithm.Concrete improvement strategies include:(1) adopt the differential mutation factor and cross factor to update the position of honey,and accept a new honey by the annealing selection strategy in the empoyed bee stage;(2) compute the probability which the every honey is selected by onlookers with tournament selection strategy in the selection stage;(3) adopt a learning factor to update the position of honey,and accept a new honey by the annealing selection strategy in the onlooker stage;(4) do the chaotic search on the optimal honey.Improved algorithm improves the global and local search ability and avoids trapping in local optimum.This paper build the model which minimizes sum of construction cost and network loss cost in planning for transmission network.The availability and effectiveness of improved artificial bee colony algorithm is proved by applying it to Garver-6-bus-system and Garver-18-bus-system.

transmission network planning;artificial bee colony algorithm ;differential evolution algorithm;chaotic search

1004-289X(2015)03-0044-05

TM715

B

2014-05-04

周智成(1989-)，男，硕士研究生，研究方向为电力系统最优运行与规划； 童买成(1985-)，男，硕士研究生，研究方向为电力系统最优运行与规划； 徐璐(1989-)，女，硕士研究生，研究方向为电力系统继电保护； 蔡婷(1985-)，女，硕士研究生，研究方向为电力系统最优运行与规划。