水中脉冲放电电压波形特性分析
2015-06-01章婧兰生王竹勤朱雨翔
章婧,兰生,王竹勤,朱雨翔
(福州大学电气工程与自动化学院,福建 福州 350108)
水中脉冲放电电压波形特性分析
章婧,兰生,王竹勤,朱雨翔
(福州大学电气工程与自动化学院,福建 福州 350108)
以冲击电压发生器波形和参数的计算模型为基础,研究了水中脉冲放电时的冲击放电电路模型,采用拉氏变换方法列出此电路方程,分析了电压波形特性,得出波前电阻数值越大电压波形峰值越低、上升越平缓,波前时间越长;波尾电阻数值越低则电压波形峰值越高,半峰值时间越长。同时对水中脉冲放电形成等离子体通道等效放电回路电压与电流振荡波形作了研究,放电过程中电路发生RLC振荡,电压初始值为30kV,电流峰值为1.5kA,水中放电等离子体通道电阻随时间变化,它不仅与电极间距离有关,而且与电容器的电容量C及初始电压值均有关。经过几个衰减振荡周期后,电阻值迅速增大,电流趋于零。计算和仿真相结合,有一定的参考意义。
脉冲电源;水中放电回路;等离子体通道;方程式;Matlab;电压波形
1 引言
为了研究电气设备在运行中遭受雷电过电压和操作过电压的作用时的绝缘性能,许多高压实验室都装设了冲击电压发生器,用来产生试验用的雷电冲击电压波和操作冲击电压波。在冲击电压发生器的设计、改造和调试过程中,需经常对波形和回路参数进行计算,因而建立冲击电压发生器波形和参数的计算模型对于简化计算和波形调试有一定的参考意义。Matlab可对冲击发生器放电回路的参数进行仿真计算,获得试验所要求的参数条件。王国枝等人[1]借助Matlab 语言的仿真功能精确计算出冲击电压发生器波形与回路参数。张春红等人[2]分析了冲击电压发生器二次回路在任意波形下的参数选择法,提出了一种采用 Matlab的数学计算功能进行冲击电压发生器在任意波形参数下的参数计算方法。T.Okamoto等人[2]建立了PD放电电路模型并列出积分方程以求解正弦电压条件下的波形,而本文针对放电形成等离子体的等效放电回路列出了积分方程求解电压及电流振荡波形。
水中脉冲放电分为水中脉冲电晕放电和水中脉冲电弧放电。两者的相同之处在于预击穿过程一样,不同之处在于电弧放电下的运动电荷载流子在水中走完从一个电极到另一个电极的全程,形成完整的等离子通道,而电晕放电未完成这一过程。本文采用的脉冲放电回路的放电形式为电弧放电。
本文建立了冲击电压发生器波形和参数的计算模型,给出了水中脉冲放电及放电形成等离子体的等效放电回路,并在Matlab仿真的基础上,进一步研究了水中脉冲放电回路与等离子体通道等效放电回路的方程式计算。
2 冲击电压发生器的基本原理
在分析设计冲击电压发生器时,忽略回路电感及测量用分压器对波形的影响,其基本放电回路如图1所示。

图1 冲击电压发生器放电回路
如图1中所示,R11与R12分别放置在波尾电阻R2的前后,其中R11为阻尼电阻,主要用来阻尼回路中的寄生振荡;R12专门用来调节波前时间Tf,称为波前电阻,其阻值可调。C1为主电容,C2为被试品及测量设备的电容,U1为主电容C1的充电电压。
冲击电压发生器的工作原理为充电电压为U1的主电容C1经阻尼电阻R11和波前电阻R12向C2充电来获得冲击电压波前的波形,而冲击电压波尾部分的波形则由主电容C1经波尾电阻R2放电来获得。国际电工委员会( IEC) 标准对冲击电压波形的定义如图2所示。

图2 冲击电压波形的定义
图2中,O1为视在原点,U2m为冲击电压幅值,Tf,Tt分别为视在波前时间和视在波尾时间,P和Q分别为波高点和半波高度。
3 冲击电压发生器的计算模型
3.1 冲击电压发生器的基本放电回路
以图1的冲击电压发生器放电回路为基础,分析输出电压波形与回路元件参数之间的关系。
波形参数放电回路的微分方程为
(1)
a=C1C2(R11R2+R11R12+R12R2)
(2)
b=C1(R11+R2)+C2(R12+R2)
(3)
设篇p1和p2为方程(1)的两个特征根,则
(4)
u2=Aep1t+Bep2t
将初始条件t=0时,u2=0;u1=U1代入以上方程可得
A=-B
u2=A(ep1t-ep2t)
则波形达到最大值u2m所需时间
则
u2m=A(ep1tm-ep2tm)
根据图2还可以计算出波形的波前时间Tf和波尾时间Tt。列出六个方程式:
由6个方程可解出6个未知数:t1,t2,t3,tm,p1,p2(其中t1
已知波前时间Tf和波尾时间Tt求解回路参数,可用试探逼近法。具体做法为,U1不变,在固定某一参数的基础上,改变其他参数进行仿真,直到得到的冲击电压波形与要求的波形相接近为止。
在利用Matlab仿真时,程序中参数C及L分别用微法和微亨作单位,这样时间t的单位为μs,电阻采用国际单位,采样频率为100MHz。采用逐次逼近法对1.2/ 50μs的标准冲击波进行运算,再将得出的值代入方程组,通过方程左右分别计算的值进行比较验证。
在上面图1的冲击电压发生器放电回路中,利用Matlab软件编程计算后,计算结果如图3所示,从图中看出波前时间为Tf=1.21μs,半峰值时间为Tt=49.95μs。
3.2 水中脉冲放电回路
冲击电压发生器应用于水中脉冲放电时,考虑回路内电感L以及水电阻R3、水电容C3的影响,所得水中脉冲放电回路如图4所示。

图3 冲击电压发生器的u2(t)波形图
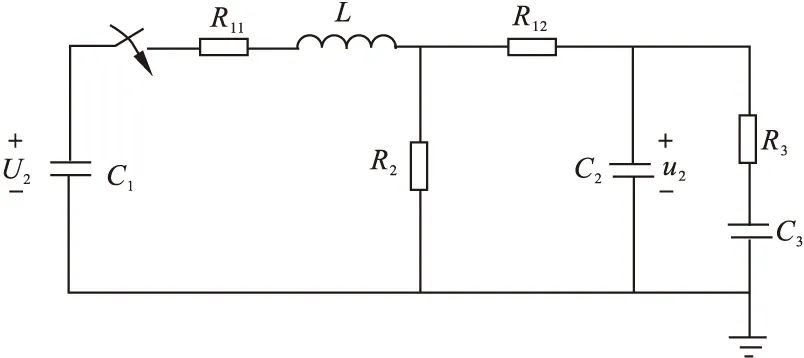
图4 水中脉冲放电回路
实际设计中,回路电感、电阻和电容等参数的影响通常不可避免,轻则改变波形参数,重则引起振荡。考虑了多种参数后的冲击电压发生器放电回路,可能为动态电路,其阶数可达3阶、4阶甚至更高阶。可采用多种计算方法来分析计算电压u2(t),如状态方程数值解法,贝杰龙(Bergeron)计算法,拉氏变换法等[5]。本文先利用拉氏变换法列出水中脉冲放电回路的电压U2(s),再借助Matlab求拉氏反变换后u2(t)的解析式。
对电路作拉氏变换并由电路理论,可求出水中脉冲放电回路的电压U2(s)为
令A=1/[(R12+R2)R3C1C2C3L],
A(1)=A[C1C3L(R12+R2+R3)+C1C2L(R12+R2)+R3C1C2C3(R12R2+R11R2+R11R12)]
A(2)=A[(R3C2C3+R11C1C3+R11C1C2)(R12+R2)+R3C1C3(R11+R2)+R12R2C1(C2+C3)+C1L]
A(3)=A[(R12+R2)(C2+C3)+C1(R11+R2)+R3C3]
A(4)=A
B(1)=AR2R3C1C3
B(2)=AR2C1
再用Matlab对U2(s)求反变换,即可得u2(t)的解析式。
可调节波前电阻R12以改变波前时间Tf,调节波尾电阻R2以改变半峰值时间Tt。保持电路其他参数数值不变,只改变R12或R2的值,得到相应的放电波形如图5、图6所示。图5、图6中纵坐标为u2(t)与u1(t)的比值,横坐标为t,单位为μs。从波形可以看出由于回路内电感L在初始时不让电流突变,使得u2(t)上升平缓。定性分析水中脉冲放电电压波形,可见R12数值越大电压波形峰值越低,u2(t)上升越平缓,波前时间Tf越长;R2数值越低电压波形峰值越高,半峰值时间Tt越长。
水中脉冲放电形成等离子通道的等效放电回路如图7所示。其中,R表示随时间变化的放电通道电阻,等离子体通道的电感和电容忽略不计,LC和RC分别为等效回路电感和电阻,C2为储能电容,U2为初始电压。
3.3 水中脉冲放电形成等离子体通道等效放电回路
水中脉冲放电形成等离子体通道过程一般分为充电和放电两部分。水中脉冲放电回路中的电容器充电到给定的电压后,触发火花间隙开关(相当于图7中的开关S闭合),将电压加到水中的棒-棒电极的间隙上(水中棒-棒电极等效为电阻R和电容C的并联,借助万用表测得等效值R=2860Ω、C=50pF)。间隙中的水介质在强电场作用下,出现分离和碰撞电离过程,从而出现从高压电极往外延伸的高电导率的根须状“先导”。当高电导率的“先导”到达对面的电极,就形成稳定的等离子体通道。该放电形成等离子通道的过程中完成了从一个电极到另一个电极的全过程,因而为电弧放电。
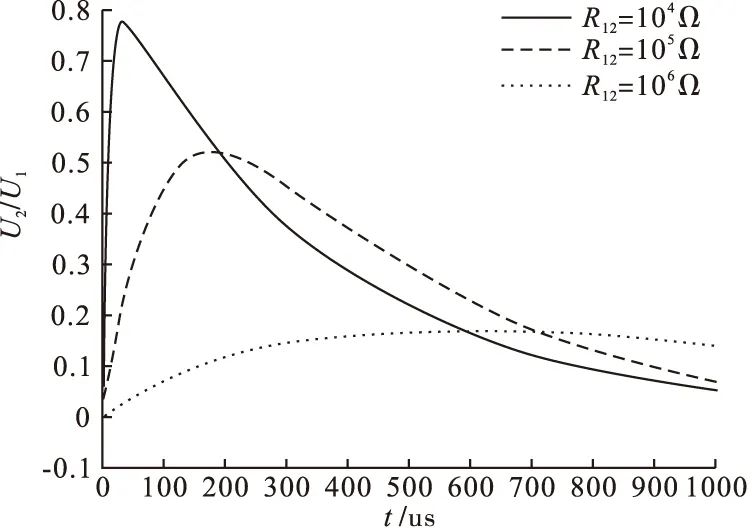
图5 水中脉冲放电回路的波前电阻R12改变时的u2(t)波形变化
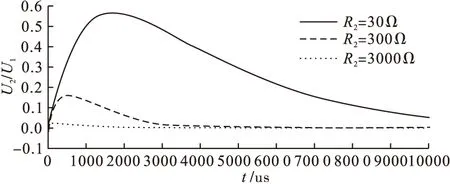
图6 水中脉冲放电回路的波尾电阻R2改变时的u2(t)波形变化
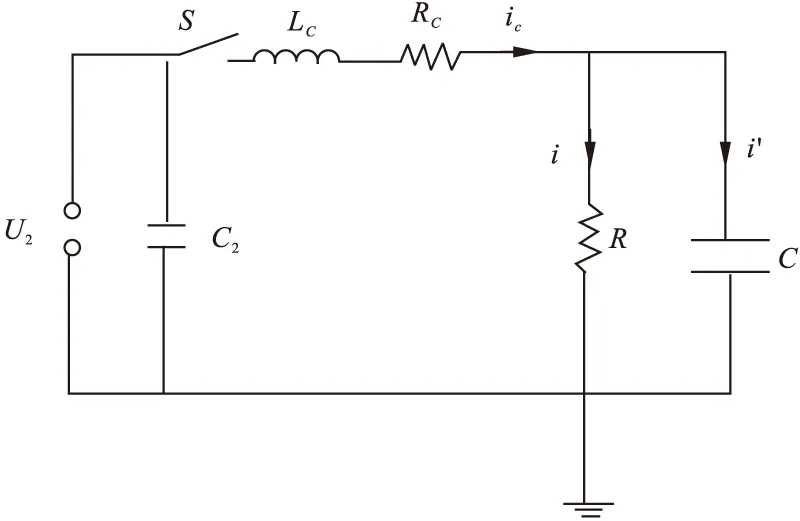
图7 等离子体通道等效放电回路
由基尔霍夫定律得到的水介质击穿形成等离子体通道时的电路过程实际上可用二阶RLC方程描述如下:
在利用Matlab仿真时,取C2=10-3μF、Lc=249nH、Rc=4.21Ω、R=2860Ω、C=50pF,电极间距离为5mm。等离子体通道等效放电回路电压波形如图8所示,电流波形如图9所示。放电过程中电路发生RLC振荡,电压初始值为30kV,电流峰值为1.5kA。

图8 等离子体通道等效放电回路电压波形
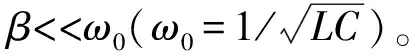
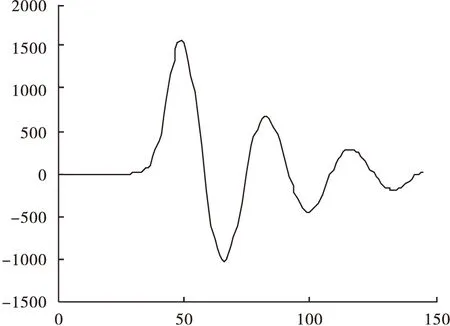
图9 等离子体通道等效放电回路电流波形
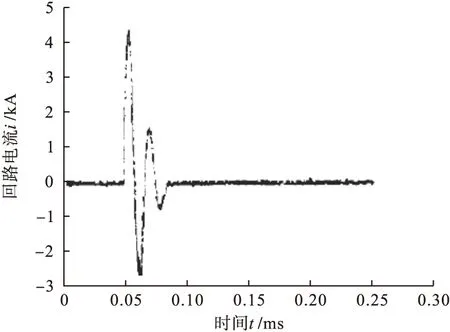
图10 电弧放电的典型电流过程波形
4 结论
本文给出了较为精确的冲击电压发生器波形计算和回路参数计算的数学模型,在此基础上进一步研究了水中脉冲放电电压波形特性,波前电阻数值越大电压波形峰值越低、上升越平缓,波前时间越长;波尾电阻数值越低则电压波形峰值越高,半峰值时间越长。列出脉冲放电回路方程式并进行了计算。对水中脉冲放电形成等离子体通道等效放电回路电压与电流振荡波形作了研究,通过计算波形与实测波形的对比得知理论计算结果与实测数据较为符合,证实了本研究方法的可行性。
[1] 王国枝,田俊梅.冲击电压发生器波形和参数的计算模型与仿真[J].山西电力,2009,151(1):58-60.
[2] 张春红,郑永康,颜怀梁.利用MATLAB 计算冲击电压发生器的参数[J].四川工业学院学报,2003,22(2):41-43.
[3] Okamoto T,Kato T,Yokomizu Y,et al.PD Characteristics as a Stochastic Process and its Integral Equation under Sinusoidal Voltage [J].IEEE Transactions on Dielectrics and Electrical Insulation,2001,8(1):82-90.
[4] Okamoto T,Takahashi T,Miyazaki S,et al.An Integral Equation for Analyzing Phase-Resolved Partial Discharge Characteristics under Sinusoidal Voltage Waveform Conditions [J].IEEE Electrical Insulation and Dielectric Phenomena,2009,9(2):401-404.
[5] 朱胜龙,叶剑涛,郁书好.冲击电压发生器放电回路数学分析及matlab在其中的应用[J].电气应用,2005,24(9):51-53.
[6] 卞文娟,杨 彬,雷乐成.液电等离子体处理有机废水[J].环境污染治理技术与设备,2003,4(5):80-84.
[7] 李伟,谢祖荣,张永丽,等.RLC 脉冲放电电路的计算机辅助分析[M].北京石油化工学院学报,2003,11(1):1-16.
[8] 张益修,孙 伟,傅正财,等.冲击电压发生器充电不均匀度的仿真和实验分析[J].电气技术,2009(2):34-37.
[9] 董 飞,魏文轩,王庆红.冲击电压发生器的MathCAD 程序设计[J].中 国 水 运,2011,11(1):91-92.
[10] 李 谦,梁智明,李 劲.火花间隙式脉冲电源脉冲电参数的影响因素[J].高电压技术,1998,24(2):32-33.
[11] 杜 涛.脉冲放电电路的仿真分析[J].探 测 与 控 制 学 报,2004,26(3):42-45.
[12] 金明剑,孙鹞鸿.不同参数条件下水中脉冲放电的电学特性研究[J].高电压新技术及应用,2004,30(7):46-49.
Analysis of the Characteristics of Voltage Waveform by Pulse Discharge in Water
ZHANGJing,LANSheng,WANGZhu-qin,ZHUYu-xiang
(College of Electric Engineering and Automation Fuzhou,Fujian 350108,China)
According to the calculation model of waveforms and parameters of impulse voltage generator,this paper researched impulse discharge circuit model of pulse discharge in water.The circuit equations were listed by using Laplace transformation method to analyzed characteristics of voltage waveform which can get the results of that the larger the wave-front resistance,the lower the peaks of voltage waveform,and the voltage rises more gentle,the wave-front time is longer.The lower the wave-front resistance,the higher the peaks of voltage waveform,and the half-peak time is longer.Voltage and current oscillation waveform of equivalent discharge circuit for plasma channel which formed by pulsed discharge in water have been researched in this paper.The circuit occurred RLC oscillation during discharge process where initial voltage is 30kV and peak of current is1.5kA.the resistance of discharge plasma channel in water changes with time,and it is not only relates to the distance between the electrodes,but also relates to the capacitance of the capacitor C and the initial voltage values.The resistance value rapidly increases and the current tends to zero after several damped oscillation cycles.The combination of calculation and simulation has a certain reference value.
pulse power supply;discharge circuit in water;plasma channel;equation;Matlab;voltage waveform
1004-289X(2015)03-0032-05
福建省自然基金项目(No.2011J1296)
TM76
B
2014-04-16
