基于EMD与NARX网络的汇率预测方法研究

马 超，徐瑾辉，蓝 斌，侯天诚，欧阳泽拯

（广东外语外贸大学金融学院，广州 510006）

基于EMD与NARX网络的汇率预测方法研究

马 超，徐瑾辉，蓝 斌，侯天诚，欧阳泽拯

（广东外语外贸大学金融学院，广州 510006）

探索构建对汇率进行直接预测的高精度组合预测算法.采用NARX神经网络作为基础模型，并结合经验模态分解模型进行混合预测，提高模型精度.为研究不同时间间隔对预测结果的影响，采用美元兑日元汇率的时间间隔为5分钟与1天的数据进行预测.实验结果显示，时间间隔较短时，模型的预测精度更高.此外，通过对汇率改革前后的人民币汇率的预测发现，汇率改革对EMD-NARX模型的预测结果影响不大，说明模型稳定性较高.

汇率预测；NARX神经网络；经验模态分解（EMD）；组合预测；误差分析

本文研究的目的便是为汇率预测寻求一种新的方法，可以对汇率进行高精度的直接预测，以此来规避汇率变动所带来的各种风险.目前国内外汇率预测主要运用的方法有支持向量机（SVM）［1］、BP人工神经网络（Artificial Neural Network）预测模型［2］、时间序列预测模型（如ARIMA）［3］、小波分析［4］等.另外，谢赤、欧阳亮等人提出神经网络组合模型具有更高的预测精度［5］，Tseng等（2002）用BP神经网络和时间序列模型—SARMIA模型进行组合，用SARMIA（Seasonal Autoregression Moving Intergrate Average）对汇率进行线性预测，再用神经网络处理SARMIA模型预测的残差，进行汇率预测［6］.用同样方法的还有Zhang（2003）用ARMIA（Autoregressive Integrated Moving Average）和ANN（Artificial Neural Networks）组合对英镑和美元汇率进行预测［7］.Yu，Wang和Lai（2005）组合广义线性自回归模型（GLAR）和神经网络进行预测［8］.受组合预测方法的启发，本文基于对NARX神经网络研究［9-10］、经验分解模型与平稳化研究［11］，创新性地提出将平稳化过程与NARX神经网络相结合对汇率进行精确预测的组合算法.

1 美元兑日元汇率预测

1.1 数据获取

本文通过比较时间间隔为5分钟与1天的汇率数据的预测结果来探究时间间隔对NARX神经网络模型与EMD-NARX混合预测模型预测结果的影响.但由于周期为5分钟的汇率数据较难获取，本文选取了NFL MetaTrader外汇交易系统中某一时间段实时记录的汇率数据（2013年8月27日—2014年5月23日），具有2万以上的样本数据量.

1.2 NARX神经网络预测

为比较不同时间间隔的预测效果，本文基于NARX神经网络模型，取隐含层节点数为10，滞后期数取10，分别采用时间间隔为5分钟和1天的原始数据作为样本来预测未来的汇率.其中，样本数据的前70%作为训练数据，后30%作为测试集进行预测.时间间隔为5分钟与1天的滚动外推预测效果如图1、2所示：

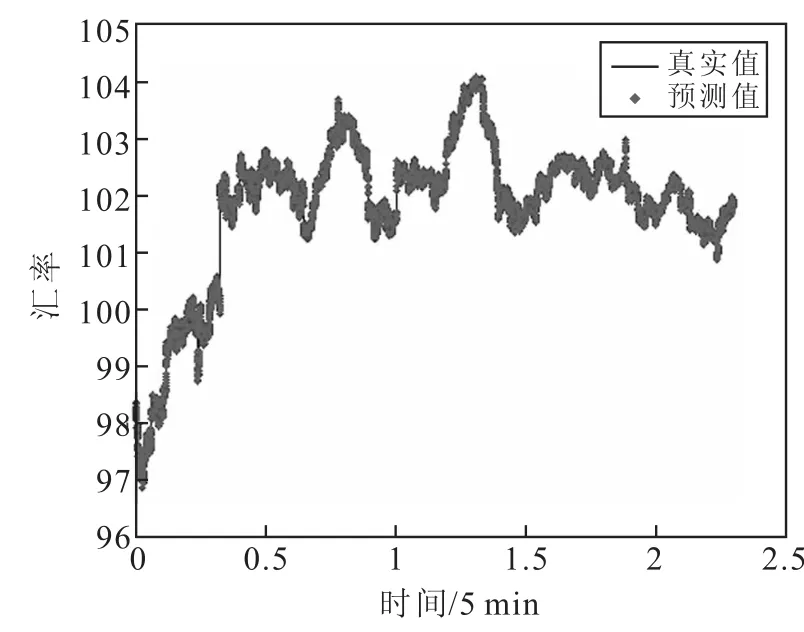
图1 间隔5分钟的滚动外推预测

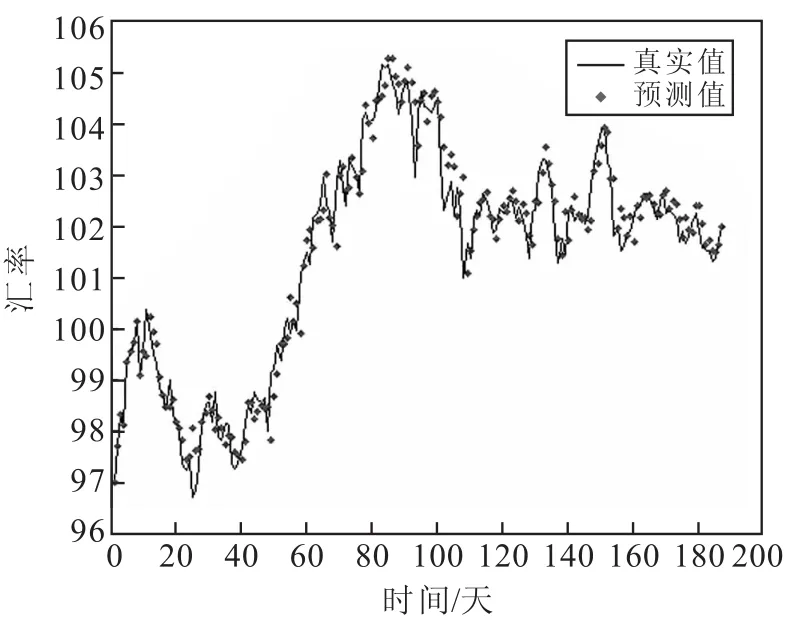
图2 间隔1天的滚动外推预测

图1为时间间隔为5分钟时NARX神经网络的预测效果图，其可决系数R2为0.997 4，均方误差（MSE）为0.000 738.图2为时间间隔为1天时NARX神经网络的预测效果图，其可决系数R2达到0.976 9，均方误差则为0.005 9.综合两个实验结果，可见NARX神经网络在汇率的预测中预测性能良好，具有优良的外推预测能力和泛化能力，精度较高.但较之基于时间间隔为5分钟的模型，基于时间间隔为1天的预测模型表现较差.

1.3 混合模型预测

汇率的时间序列具有较大的不平稳性，即使运用动态神经网络进行预测，也存在一定的误差.因此，为了提高模型的精确度，本文对时间序列运用EMD模型来降低其非平稳性，然后对每一频带分别进行NARX神经网络预测，最后将各分量的预测结果进行等权求和，得到最终的预测结果，并求出均方误差.

同样，在混合模型的预测中，为研究不同时间间隔对预测结果的影响，本文分别对时间间隔为5分钟与1天的美元兑日元汇率进行了滚动预测.其中NARX神经网络模型取隐含层节点数为10，滞后期数取10，且训练集取前70%的数据，剩下的数据为测试集.结果分别如图3、4所示：

图3 间隔5分钟的滚动外推混合预测

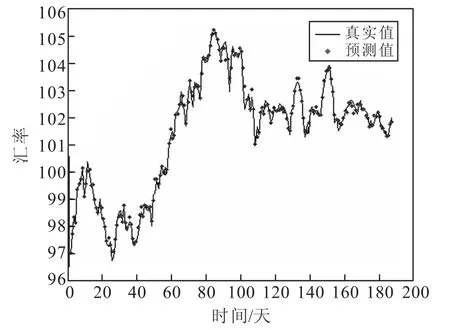
图4 间隔1天的滚动外推混合预测

1.4 误差分析

在各模型中，均取前70%的数据为训练数据，剩余的为测试数据.实验显示，可决系数R2以及均方误差（MSE）如表1所示：

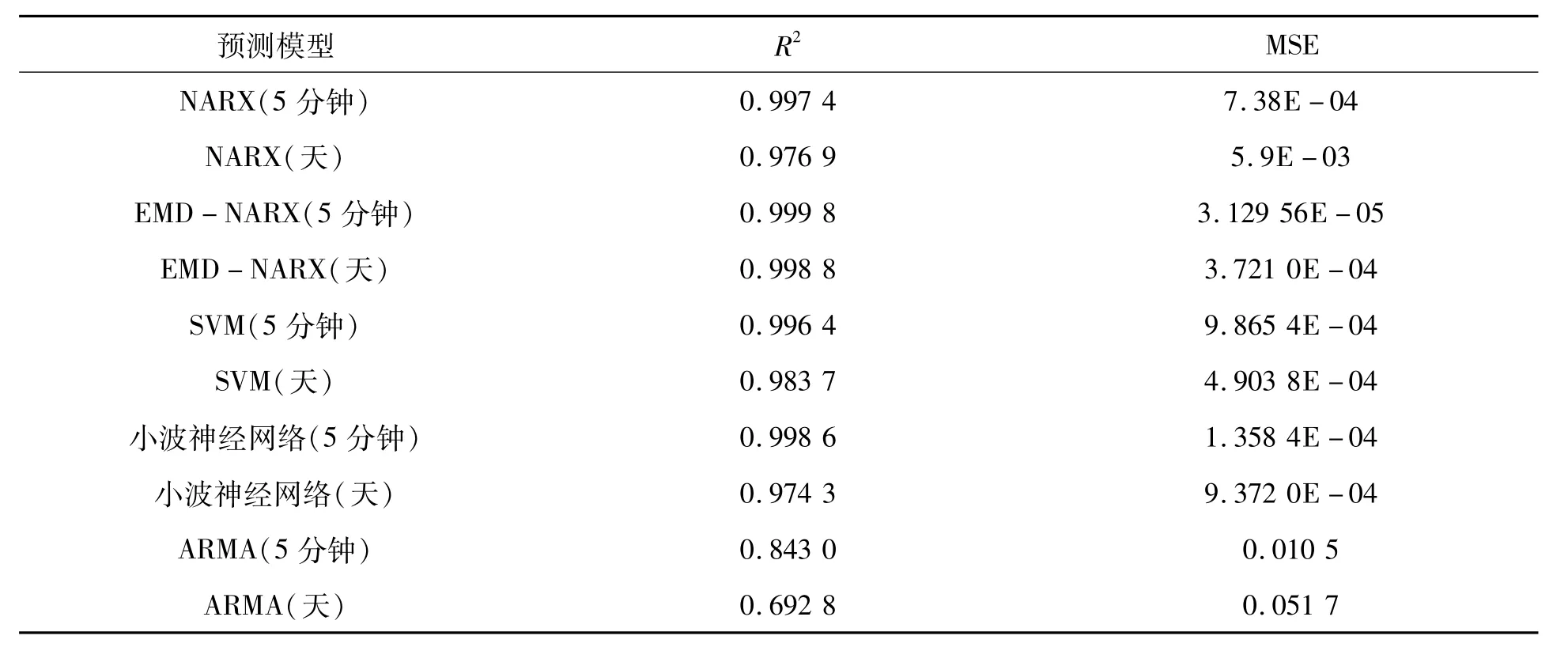
表1 预测误差分析

表1所总结之实验结果表明，在时间间隔为5分钟的情况下，各模型的预测准确度均高于时间间隔为1天的情况；而基于神经网络类模型的函数逼近方法的效果远优于传统时间序列预测方法（ARMA）.其中，在5分钟间隔的数据采样下，本文所提出的EMD-NARX模型取得了最好的效果，其均方误差仅为3.129 56E-0.5，R2可决系数为0.999 8，表明模型具有优异的逼近能力.NARX与EMD分解方法的结合，能够在去除数据噪音的同时，充分挖掘时间序列数据下所隐藏的非线性规律.这对于人们发现汇率的变动规律与趋势，具有较高理论意义和实用价值.

2 人民币汇率预测

除了探究NARX神经网络与EMD-NARX混合预测模型在汇率预测中的适用性，本文通过观察人民币汇率改革对各种模型预测结果的影响来探究模型的稳定性.

2010年6月19日，中国人民银行新闻发言人以答记者问的形式发布消息，加强人民币的弹性，以此推动汇率制度改革的深入进行，业界称之为二次汇改.与第一次汇改不同，中国的内部经济金融环境发生了很大变化.这些因素可能会对本文的实验结果造成影响.

为了探究二次汇改是否对本文的预测模型有影响，本文选取美元兑人民币汇率的历史数据，数据从2005年1月1日起，至2010年12月31日，样本间隔为1天.其中，2005年到2008年的数据作为训练数据，2009年到2010年的数据作为测试数据.数据来源于国家外汇管理局.网址为：http：//www.safe.gov.cn/.下面将数据分别代入到NARX神经网络与EMD-NARX混合预测模型中进行实验，预测效果如图5、6所示：

图5 NARX神经网络的滚动外推混合预测

图6 EMD-NARX混合模型的滚动外推混合预测

从上述两个效果图可以看出NARX神经网络与EMD-NARX混合模型同样适用于人民币汇率的预测，且有较高的精度.但是通过对比，在网络测试的前期，NARX神经网络的预测效果与EMD-NARX混合模型准确度相似.但在网络测试的中后段，也就是第二次汇率改革的时候，图5中预测值与实际值的误差明显比图6中的要大.

为了进一步探究发生汇率改革时模型的稳定性，本文采用了R2与MSE作为误差分析的指标，运用目前为止国内外研究文献中部分常用的算法来进行汇率预测，并与NARX神经网络、EMD-NARX混合预测模型的预测结果进行对比.其中，“无汇改”的数据为2005年1月1日到2008年12月31日，且前70%的数据为训练集；“有汇改”的数据为2005年1月1日到2010年12月31日，且以前三年的数据作为训练集，后两年的数据作为测试集.具体的误差分析对比如表2所示：

表2 预测误差分析

从表2中，我们不难看出，汇改这一因素的加入会导致多数模型的预测误差增大.对于多数神经网络的模型，汇改发生后需要进行重新的网络训练.但本文中，由于EMD过程的加入，使得EMD-NARX模型的抗噪音能力和鲁棒性都有了较大提升.在不重新训练的前提下，其在汇改后的测试数据上依然展现出了较强的逼近能力，MSE依然为各模型中最小值，只有1.522 5E-04，能准确地对汇率做出预测.另外，其均方误差和R2可决系数甚至优于基于无汇改数据进行测试的SVM、小波神经网络、ARMA等模型.从另一个角度亦可看出，汇改后汇率的变动规律的确发生了微小变化，但不会使本文提出之模型的预测效果出现明显降低.

3 结语

实验结果表明，EMD-NARX模型比NARX神经网络更为精确，且NARX神经网络与EMD-NARX混合预测模型都具有比目前国内外文献中常用模型更低的误差.另外，通过对比分析，得到了选取时间间隔为5分钟的数据进行预测时效果更佳的结论，且在众多的模型中，本文构建的EMD-NARX混合预测模型具有更强的稳定性，对汇率预测、投资决策等实际领域具有重大的参考意义.

［1］ 杨新臣.基于支持向量机的非线性汇率预测分析［J］.理论新探，2010（18）：13-16.

［2］ 余乐安，汪寿阳，黎建强，等.基于BPNN和Web的智能外汇滚动预测与交易决策支持系统的开发［J］.管理学报，2005（9）：109-114.

［3］ 欧阳昕.基于时间序列ARIMA模型的人民币汇率走势预测［J］.现代经济信息，2011（16）：218-219.

［4］ 郑纪安.基于小波分析和神经网络的金融时间序列预测研究［D］.厦门：厦门大学，2009.

［5］ 谢赤，欧阳亮.汇率预测的神经网络方法及其比较［J］.财经科学，2008（5）：47-53.

［6］ MICHAEL Y H，CHRISTOST.Combining conditional volatility forecasts using neural networks：an appl-ication to the EMS exchange rates［J］.Journal of International Financial Markets，Institutions and Money，1999（9）：407-422.

［7］ TSENG Fang-mei，YUBHsiao-cheng，TZENGGwo-hsiung.Combining neural network modelwith seasonal time series ARIMAmodel［J］.Technological Forecasting&Social Change，2002，69：71-87.

［9］ YU Lean，WANG Shou-yang，LAIK K.A novel nonlinear ensemble forecasting model incorporating GLAR and ANN for foreign exchange rates［J］.Computers&Operations Research，2005，32：2523-2541.

［9］ 李明，杨汉生，杨成梧，等.一种改进的NARX回归神经网络［J］.电气自动化，2006，28（4）：6-8.

［10］李挺，雷霞，张学虹，等.基于NARX神经网络预测及模糊控制的互联电网CPS鲁棒控制策略研究［J］.电力系统保护与控制，2012，40（14）：58-62.

［11］HUANG N E，SHEN Z，LONG SR，et al.The empiricalmode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis［J］.Proceedings of the Royal Society of London.Series A：Mathematical，Physical and Engineering Sciences，1998，454（1971）：903-995.

［责任编辑王新奇］

On Exchange Rate Forecasting M ethod Based on EMD and NARX Neural Network

MA Chao，XU Jin-hui，LAN Bin，HOU Tian-cheng，OU-YANG Ze-zheng

（School of Finance，Guangdong University of Foreign Studies，Guangzhou 510006，China）

We have explored the high-precision combined calculation for direct exchange rate forecast.We adopt the NARX neural network as the originalmodel.In order to enhance the forecast precision，a forecasting method based on empirical decomposition mode is also proposed.To explore the effects of various time intervals on the prediction outcomes，the 5-minute and daily data between US$and Japanese Yen exchange rates are used respectively in the experiments.The forecasting results indicate that the precision is higher when the time interval is shorter.Besides，by forecasting the exchange rate of RMB before and after the exchange rate reform，we discover that the exchange rate reform has little effect on EMD-Narx model，which means that themodel is relatively stable.

exchange rate forecasting，NARX neural network，empiricalmode decomposition；combined forecasting；error analysis

TP183

A

1008-5564（2015）02-0070-05

2014-12-10

国家级大学生创新训练计划资助项目（201411846001）

马 超（1993—），男，广东佛山人，广东外语外贸大学金融学院学生，主要从事数据挖掘，人工智能及其在工程领域的应用研究.