三维热弹性系统的柯西问题

王 超

（南京航空航天大学理学院数学系，南京 211106）

三维热弹性系统的柯西问题

王 超

（南京航空航天大学理学院数学系，南京 211106）

研究热弹性系统的柯西问题，假设初始数据的H3范数是足够小的，但更高阶导数的范数可以任意大.采用带插值的纯能量方法，通过对热弹性系统方程组做先验估计得出能量不等式，继而得出热弹性系统存在唯一的整体解.

能量估计；插值；整体存在性

一维热弹性系统，刻画了热弹性效应中非线性弹性波的传播过程，本文我们考虑的模型如下：

其中x∈ℝ，t≥0.这里σ(z)是z的光滑函数，而且满足σ＇(z)＞0，σ＇(0)=a＞0.参数β，η，δ，τ和κ是正常数.其中参数β是热膨胀系数，η是热传导系数.未知函数是u(x，t)，θ(x，t)，q(x，t)，分别表示形变速度，温度，还有热通量.

下面，我们给出文章的主要结论：

定理1 假设U0∈HN(ℝ3)，N≥3.那么这里就存在着某个足够小的常数ε＞0，使得如果有

那么这个问题（1）就存在着一个唯一的整体解U(x，t)满足对所有的t≥0，都有

成立.这里U(t)=(v，z，θ，q)T，C0是正常数，l=0，1…，N-1.

1 非线性能量估计

在这一部分中，我们利用系统（1）得到先验的非线性能量估计，这里我们首先做一个先验假设，对充分小的ε＞0，N≥3，我们假设有

下面，我们证明包含耗散项q的能量估计.

引理1假设0≤k≤N-1，那么我们有下面的式子成立：

证明对于0≤k≤N-1，将∇k作用到（1）4，然后（1）1两边同乘上κδ∇kv，（1）2两边同乘上κδ（σ＇（z）∇kz），（1）3两边同乘上κβ∇kθ，（1）4两边同乘上ηβ∇kq，最后四个方程相加，在ℝ3上积分，我们得到：

这里

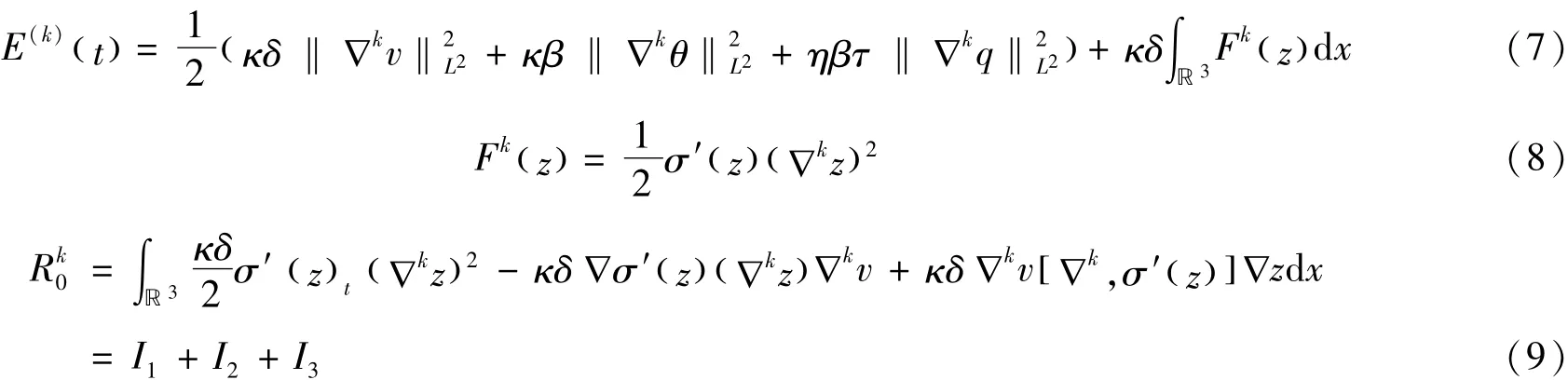
首先，我们来估计I1，

这里α满足

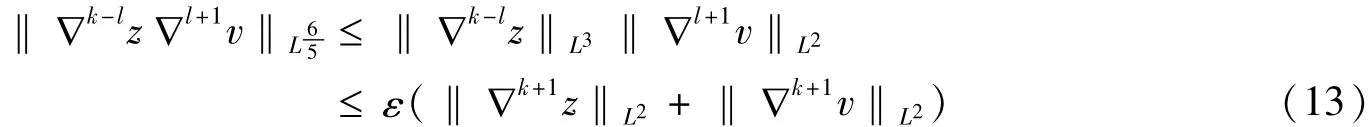
这里α满足

由上述推算，我们可以得到

同理可得

下面，我们来估计I3，

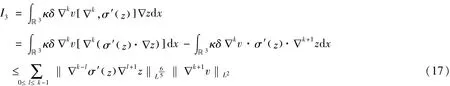
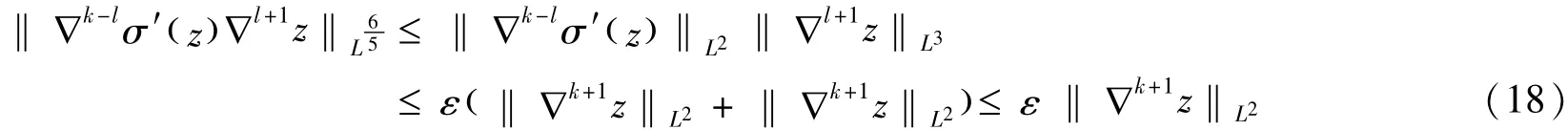
这里α满足

这里α满足

所以我们由上述推理可以得到

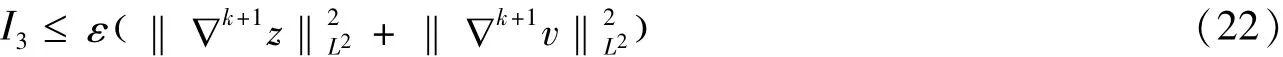
最终，我们得到

推论1由引理1的证明方法可以知道，假设0≤k≤N-1，那么我们有

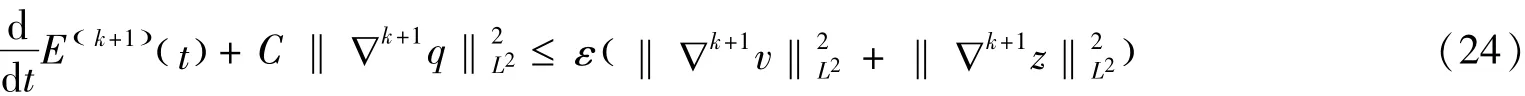
成立，具体证明方法和过程可参照引理1.这里不再赘述.

下面，我们将会利用方程组（1）得到包含z，θ，v项的能量估计.

引理2假设0≤k≤N-1，那么我们有下面的式子成立：

证明令0≤k≤N-1，用∇k作用到（1）4式，然后等式两边同剩∇k+1θ得

对上式关于x在ℝ3上积分得

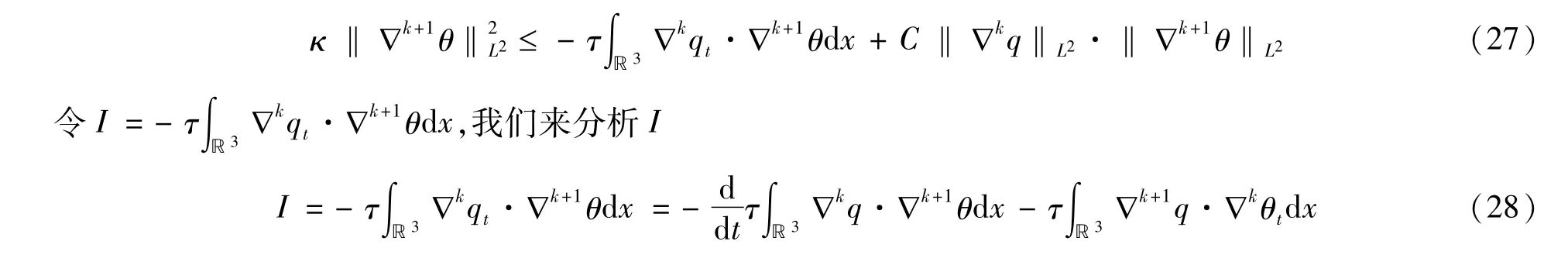
由方程（1）4，我们得到

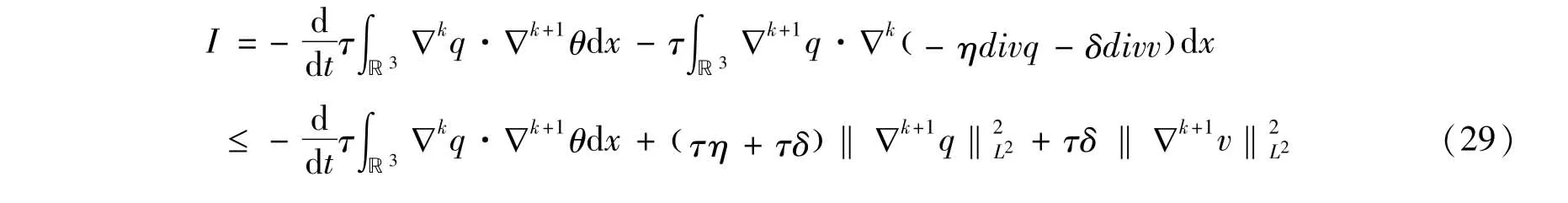
由以上推算，我们得到

接下来，我们用∇k作用到（1）3式上，然后等式两边同剩∇k+1v得

对上式关于x在ℝ3上积分得

利用方程（1）1，我们有

当l=0时，我们有

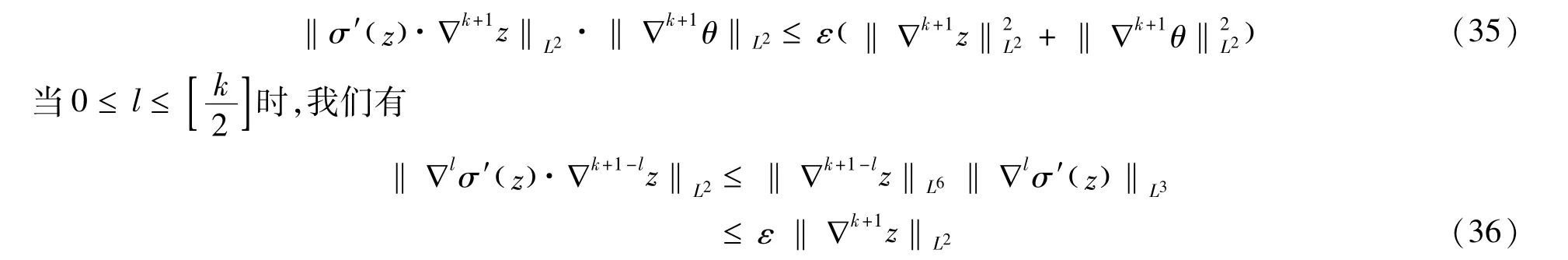
这里α满足

这里α满足

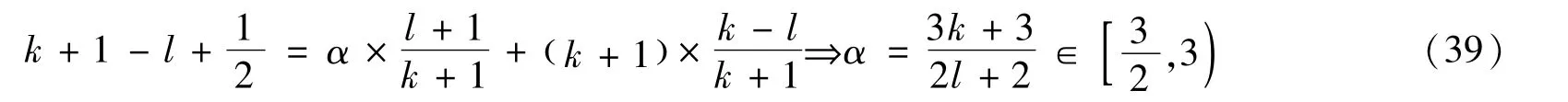
所以，由以上推算，我们可以得到

下面，我们重写方程（1）1如下

这里m＞0，然后用∇k作用到（41）式上，然后等式两边同剩∇k+1z得

对上式关于x在ℝ3上积分得

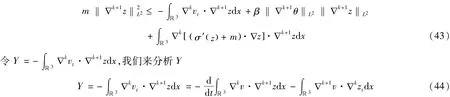
由方程（1）2我们得到

当l=0时，我们有

这里α满足

这里α满足

所以，由以上推算，我们可以得到

我们对（30），（40），（52）三个不等式整合和配系数就可以得到（25）式.

2 定理的证明

在这一部分，我们将会结合在第一部分中得到的能量不等式来证明定理1.

令N≥3，0≤l≤m-1且3≤m≤N.对引理1的（5）式，令k从l到m-1加起来，对推论1的（24）式，令k=m-1，得到的两式相加得

对引理2的（25）式，令k从l到m-1加起来，我们有

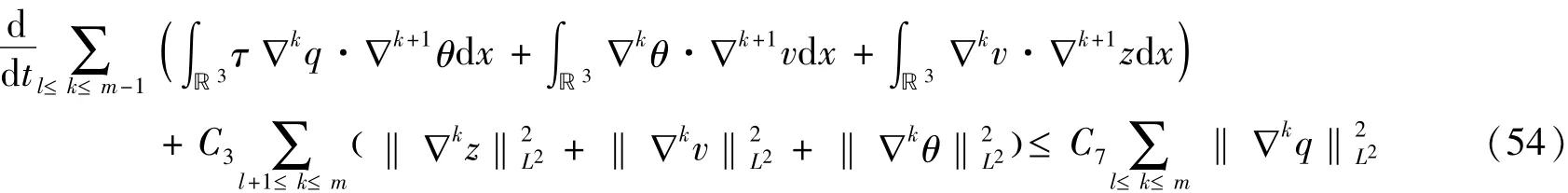
（54）式两边同时乘上2C6ε/C3，然后加上（53）式，由于ε＞0非常小，我们可以推断出这里必然存在着一个常数C8＞0，使得当0≤l≤m-1有

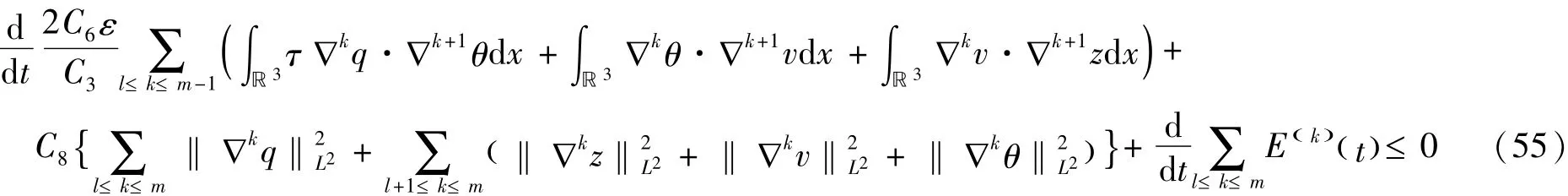
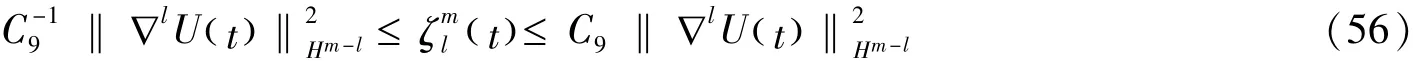
对于0≤l≤m-1，我们重写（55）式如下

在上式中取l=0，m=3，然后关于时间积分，得到

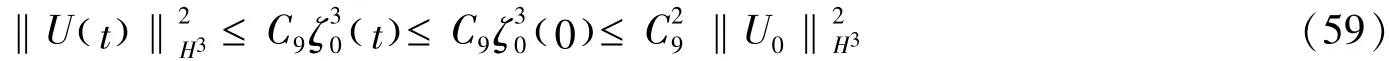
如果我们假设‖U0‖H3≤ε，这样就封闭了先验的估计‖U()t‖H3≤ε，N≥3，反过来，我们可以在（57）

式中取l=0，3≤m≤N，然后关于时间积分得

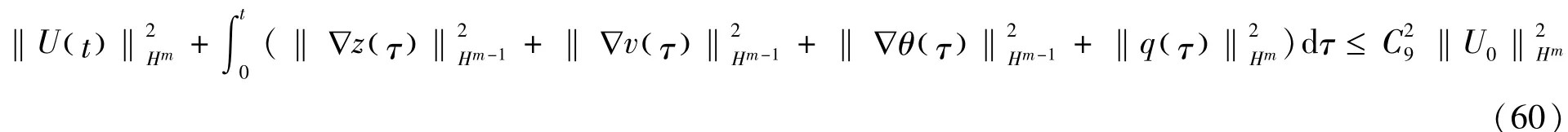
这样，我们就证明了定理1.

［1］ TAN Z，WANG Y.Global solution and large-time behavior of the 3Dcompressible Euler equations with damping［J］.Differential Equations，2013，254（4）：1686-1704.

［2］ SOHINGER V，STRAIN R M.The Boltzmann equation，Besovspaces and optimal time decay rates in$R-xˆn$［J］.Advances in Mathematics，2014，261：274-322.

［3］ GUO Y，WANG Y J.Decay of Dissipative Equations and Negative Sobolev spaces com-munications in Partial Dikerential Equations［J］.2012，37（12）：2165-2208.

［4］ KASIMOVA A，RACKEB R，SAID-HOUARIA B.Global existence and decay of solutions of the Cauchy problem in thermoelasticity with second sound［J］.Applicable Analysis：An International Journal，2014，93（5）：911-935.

［5］ TAN Z，Wang H Q.Optimal decay rates of the compressiblemagnetohydrodynam-Ic equations［J］.Nonlinear Analysis：RealWorld Applications，，2013，14（1）：188-201.

［6］ HRUSAW J，MESSAOUDISA.On formation of singularities on one-dimensional nonlinear thermoelasticity［J］.Archive for Rational Mechanics and Analysis，1990，111：135-151.

［7］ HU Y，RACKE R.Formation of singularities in one-dimensional thermoelasticity with second sound［J］.Quart.Appl. Math.，2014，72：311-321.

［责任编辑王新奇］

The Cauchy Problem in the 3D Thermoelasticity

WANG Chao

（Department of Mathematics，School of Science，Nanjing University of Aeronautics and Astronautics，Nanjing 211106，China）

This study is on the Cauchy problem in the 3D thermoelasticity.We assume that the H3norm of the initial data is small，but the higher order derivatives can be arbitrarily large. Pure energymethod with interpolation is adopted.Based on thermal elastic system equations，a priori estimate is done.The outcome is the energy inequality.We conclude that there is a unique global solution to thermoelastic system.

energy estimate；interpolation；global existence

O175.29

A

1008-5564（2015）02-0001-06

2014-11-16

王 超（1990—），男，山东济宁人，南京航空航天大学理学院数学系硕士研究生，主要从事偏微分方程研究.