基于EMD的多特征参数和关联向量机的滚动轴承故障诊断研究

娄 洁，李雅芹

（1.芜湖职业技术学院汽车工程学院，安徽 芜湖 241006；2.中健科仪有限公司，江苏 无锡 214062）

基于EMD的多特征参数和关联向量机的滚动轴承故障诊断研究

娄 洁1，李雅芹2

（1.芜湖职业技术学院汽车工程学院，安徽 芜湖 241006；2.中健科仪有限公司，江苏 无锡 214062）

轴承作为工业中旋转机械中的重要部件，其故障将严重影响机械设备的安全运行.为了实现对轴承运行故障状态的有效诊断，提出了一种基于经验模态分解（empiricalmode decomposition，EMD）提取的多特征参数的关联向量机的（Relevance vectormachine，RVM）的滚动轴承的多故障诊断模型.首先运用经验模态分解的方法将轴承振动信号分解为多个固有的模态分量，之后将提取的表征轴承故障特征的IMF分量的能量、峭度、偏度构造特征向量，最后采用关联向量机多分类故障诊断模型进行故障模式识别.轴承实测振动信号分析表明：该方法能够有效、准确地诊断出轴承的故障状态，具有较高故障诊断准确率.

EMD分解；多特征参数；关联向量机；故障诊断

滚动轴承是机械设备中的重要部件，是汽车传动系统的基础部件，素有“汽车产业的关节”之称，其运行状态的正常与否将直接关系到整车的安全性和可靠性.若汽车的故障轴承未被及时检测出来，极有可能导致整个汽车系统瘫痪，汽车无法正常运行，所以开展对滚动轴承进行状态监测和故障诊断分析的研究成为当前的研究热点.

非线性，非平稳性以及时变的特性是滚动轴承振动信号所具有的复杂信号特性，正是由于这些复杂的信号特征导致常见的小波分析，傅里叶分析等［1-2］信号处理技术难以进行有效的故障诊断，因此从复杂的振动信号中提取故障特征并分离故障模式成为当前的研究热点.Huang［3-5］等提出的时频分析方法—经验模态分解（empiricalmode decomposition，EMD），通过有效的把握信号的局部特征，将信号细分为若干个固有模态函数（Intrinsicmode function，IMF）之和［6］，在不用选择基函数的基础上可以根据信号自身的特点分解出能够突出数据局部特征的各个IMF分量.但是由于滚动轴承的尺寸以及故障位置的不同，使得依靠模态分解后的频谱图分析故障位置的效果不太理想.为了解决上述问题，本文提出利用经验模态分解后表征轴承故障诊断信息的若干个固有模式函数（intrinsic mode funnction，IMF）的能量、峭度以及偏度作为关联向量机的特征参数进行故障诊断分类，成功实现了滚动轴承的故障诊断.

1 滚轴轴承故障特征多参数提取

1.1 经验模态分解（EMD）

经验模态分解其本质上是对一个信号进行稳态化处理，它基于信号的局部特征时间尺度，能够将信号分解为若干个固有模态函数IMF之和［7］，进一步分析各个IMF分量可以更精准地把控原始数据的特征信息.如上所述，原始信号分解为

式中，y（t）是原始信号，m1（t），m2（t），…，mn（t）为y（t）的n个IMF分量，rn（t）是残余函数.各个IMF分量分别包含了信号从高到低的不同频率段的成分信息，且随信号本身变化而变化.从分解过程中可以看出，EMD将IMF分量由高频到低频依次分解出来.文献［8］中提到滚动轴承损伤故障信号通常往往被调制到高频，所以使用EMD对滚动轴承进行分解得到的前几个分量往往包含了故障信号特征，从而实现将振动故障信号中的低频干扰和噪声分离出去.

滚动轴承内圈有故障时的驱动端的振动信号以及前5个IMF分量如图1所示，从图中可以看出，EMD分解把故障信号的特征在不同的分辨率下显示出来.

1.2 EMD分解的多特征参数提取

采用经验模态分解的方法对滚动轴承振动信号处理后，计算出前几个IMF分量，然后提取IMF分量的能量Ei，峭度Ki和偏度Si的多个特征参数.能量、峭度以及偏度的计算方法［9］如下：

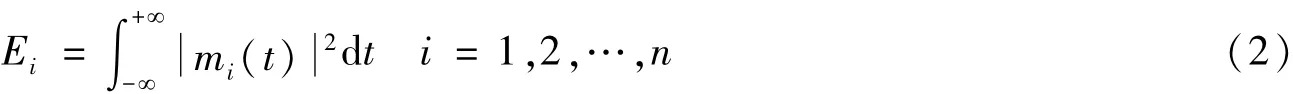
归一化后的能量Ti为：

IMF分量的峭度为：

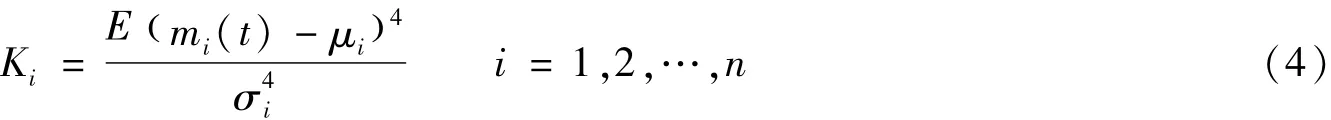
IMF分量的偏度Si为：

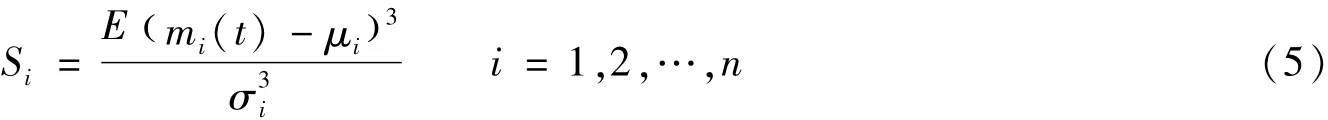
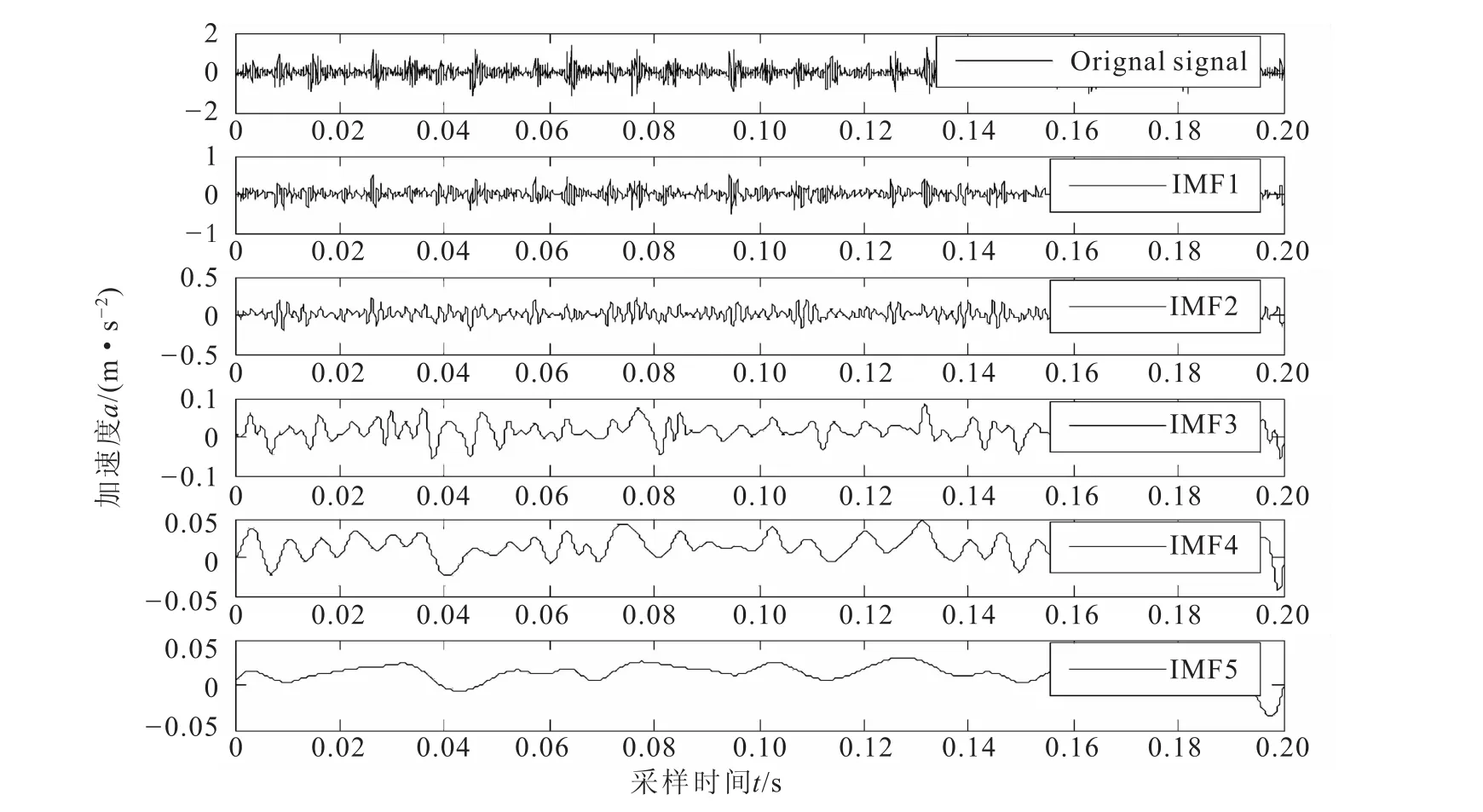
图1 内圈故障的时域波形及EMD分解后的IMF分量图

2 相关向量机

文献［10］在基于贝叶斯理论的框架下提出了一种新的机器学习方法——关联向量机（Relevance Vector Machine，RVM），与支持向量机相比，它能够进行点的分布预测，而且解更为稀疏，具有更好的泛化能力.

设｛xn，yn｝为给定的输入、输出训练样本集，且均服从相互独立分布.输入样本x和目标值y之间的关系表示为［11］：

yn=f（xn，ω）+εn，其中噪声εn服从高斯分布：εn～N（0，σ2），其均值为0，方差为σ2.

关联向量机的分类模型输出为：

其中w=［ω1，ω2，…，ωn］T为权重，K（x，xi）为核函数，φ是核函数组成的结构矩阵，由于目标值yn独立，所以整个数据集的似然函数［9］为：

其中：

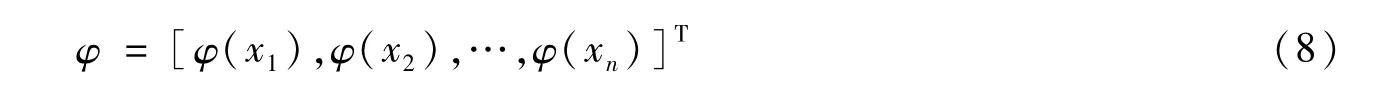
φ的每行表达式为φ（xn）=［1，k（xn，x1），…，k（xn，xN）］.求解ω和σ如果径直用最大似然法估计，通常会出现过学习的问题，即ω中不为0的元素占大部分［11］.为避免过拟合的出现，确保模型的稀疏性，稀疏贝叶斯对权重向量w赋予零均值高斯先验分布：

其中，α=（α0，α1，…，αN），求解权重ω的问题在假设超参数α与噪声参数σ2均服从Gamma先验概率分布前提下，可以转化为求解超参数α的问题，当α→∞时，ω→0.

3 EMD多特征参数与关联向量机的滚动轴承故障诊断系统

虽然传感器采集到运转过程中的滚动轴承的信号非常复杂，具有时变、非线性等特点，利用EMD经验模态分解对振动信号提取多个IMF分量并且分别计算能量、峭度和偏度等特征参数能够有效的表征轴承的运行状态，作为关联向量机（RVM）多故障分类器的输入特征参数，从而实现轴承的故障状态准确识别.其具体的步骤如下：

（1）采用经验模态分解的方法对采集到的轴承振动信号数据进行分解，提取包含主要故障的前5个IMF分量m1～m5，并计算IMF分量的能量、峭度和偏度等多个特征参数；

（2）选择高斯核函数作为关联向量机的核函数；

（3）选择多个不同的输入特征向量，建立不同的故障诊断模型，从而获得N个不同的关联向量机分类器模型；

（4）关联向量机滚动轴承的多故障诊断系统的构建是通过以二叉树的方式将上述的N个关联向量机组合起来；

（5）最后，将EMD经验模态分解提取的多个特征参数的测试样本输入到相应的关联向量机组成的多故障诊断模型中进行测试，实现滚动轴承的多故障诊断分析.

4 诊断实例研究

4.1 诊断应用与分析

为了验证上述诊断系统的有效性，本文利用美国凯斯西储大学电气工程［12］实验室的滚动轴承实验数据.选用型号为6205-2RS的深沟球轴承，由电火花机在轴承内、外圈人工加工制作轴承局部损伤（坑点），数据的采样率为12 kHZ，数据文件包含了正常、外圈，内圈以及滚动体等四种故障状态的数据.每种状态均在转速为1 700 r/min的转速下随机采集各50组，总计200组，每组的采样点数为2 400点，其中随机选取120组作为训练样本，80组作为测试样本.

4.2 特征提取

表1 轴承故障特征向量

为了有效的诊断滚动轴承的故障模式，对轴承4类状态（正常、内圈、外圈、球体）的轴承驱动端振动信号分别进行EMD分解，提取前几个IMF分量的能量、峭度、以及偏度来表征故障模式的特征向量，作为多模式故障诊断模型的特征向量.表1只列出了各个状态的某个样本经过EMD分解提取第一个IMF分量的多个特征参数.

4.3 多故障诊断模型的建立及结果分析

采用二叉树的方法建立多故障诊断分类模型，首先，利用能量作为特征参数，将正常状态和故障状态（外圈，球体，内圈）训练正常（类别为+1）、故障（类别为-1）的两类关联向量机的诊断模型RVM1，之后利用能量，峭度、偏度作为特征参数，分别建立内圈（类别为+1）和球体、外圈（类别为-1）的二分类诊断模型RVM2，并建立球体（类别为+1）和外圈（类别为-1）的二分类诊断模型RVM3.最后将测试数据集通过经验模态分解提取的多测试数据集进行预测，得到多模式诊断分类的结果.结果类别如表2所示.

表2 不同故障诊断RVM测试结果故障状态表

为了验证关联向量机（RVM）多故障诊断诊断模型对轴承状态的诊断效果，分别用关联向量机和最小二乘支持向量机2种诊断模型进行仿真.故障的诊断结果如表3所示.

从表3中可以看出，本文提出的方法比SVM提出的方法有更好的效果，能够成功实现轴承的故障诊断分析.

表3 不同故障诊断多分类的识别结果

5 结语

针对滚动轴承的非线性、时变、非平稳的振动信号，提出了一种基于经验模态分解与关联向量机的滚动轴承故障诊断方法，实验表明，通过经验模态分解对轴承驱动端提取的IMF分量后，计算出的能量、峭度、偏度等多个特征参数能够有效地区分滚动轴承不同故障状态.在进行滚动轴承不同故障状态的特征提取的基础上建立的轴承故障状态的关联向量机的多分类模型，可以有效地识别滚动轴承的故障状态，与支持向量机多故障模型相比较，具有更好的适应性.

［1］ 白冬梅，邱天爽，鲍海平.基于经验模式分解与样本熵的癫痫预测方法［J］.中国生物医学工程学报，2006，25（5）：6 -11.

［2］ 王冬云，张文志.基于小波包变换的滚动轴承故障诊断［J］.中国机械工程，2012，23（3）：295-298.

［3］ HUANG N E.The empiricalmode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis［J］.Proc.R.Soc.Lond A，1988，454：903-995.

［4］ 周川，刘畅，伍星，等.基于EMD和自适应形态学滤波的调解方法极其应用研究［J］.机械科学与技术，2011，30（8）：1376-1380.

［5］ 王金东，代梅，夏法锋，等.基于EMD信息熵和支持向量机的往复压缩机轴承故障诊断［J］.流体机械，2014，42（7）：43-46.

［6］ 焦卫东，朱有剑.基于EMD的轴承故障包络谱分析［J］.轴承，2009（1）：47-49.

［7］ 杨宇，于德介，程军圣.基于经验模态分解的滚动轴承故障诊断方法［J］.中国机械工程，2004，15（10）：908-911.

［8］ 裴骏峰，毕昆泪，吕苗荣，等.基于多特征参数和概率神经网络的滚动轴承故障诊断方法［J］.中国机械工程，2014，25（15）：2055-2058.

［9］ TIPPING M E.Sparse Bayesian learning and the relevance vector machine［J］.Journal of Machine Learning Research，2001，1（3）：211-244.

［10］DONG Chao，ZHAO Hui-jie.Hyperspectral image classification and application based on relevance vector machine［J］. Journal of Remote Sensing，2010，14（6）：1273-1278.

［11］李强，皮智谋.基于独立分量分析和相关向量机的轴承故障诊断研究［J］.制造业自动化，2014，36（8）：6-9.

［12］CaseWestern Reserve University Bearing Data Center.Download a Data File［EB/OL］.Http：//csegroup.case.edu/bearingdatacenter/pages/normal-baseline-data.

［责任编辑王新奇］

EMD-Based M ulti-Feature Parameter and RVM for Rolling Bearing Fault Diagnosis

LOU Jie1，LIYa-qin2

（1.School of Automotive Engineering，Wuhu Institute of Technology，Wuhu 241006，China；2.Biox Instrument Co.，LTD，Wuxi214062，China）

Rolling bearing is a significant component in rotatingmachinery.Its faultswould seriously affect the safety ofmachine operation.In order to achieve effective fault diagnosis of rolling bearing，an EMD-Based multi-feature parameter and RVM method for rolling bearing multi-fault diagnosis is proposed.First，themode decomposition（EMD）method is adopted for decomposing fault vibration signals into several intrinsicmode functions（IMFs）.Next，the Energy，Skewness and Kurtosis of the instantaneous amplitudes of the IMFs are extracted as the feature vector.Finally，the EMD-based multi-feature parameter RVW model is used for the failuremode identification.An analysis of bearing vibration signals indicates that thismethod iseffective in diagnosing the bearing faults and features high accuracy.

empiricalmode decomposition；multi-feature parameter；RVM；fault diagnosis

TN911.72

A

1008-5564（2015）02-0028-05

2014-12-16

安徽省教育厅自然科学研究重点项目（KJ2014A282）

娄 洁（1976—），女，山东临沂人，芜湖职业技术学院汽车工程学院副教授，硕士，主要从事汽车及其零部件制造和新能源汽车研究；

李雅芹（1983—），女，山东海阳人，中健科仪有限公司工程师，硕士，主要从事数据处理，模式识别分析建模，故障诊断研究.