曲线地段地铁诱发的大地振动规律探讨

张燕

(华东交通大学 土木建筑学院，江西 南昌 330013)

曲线地段地铁诱发的大地振动规律探讨

张燕

(华东交通大学 土木建筑学院，江西 南昌 330013)

以南昌地铁1号线的某标段工程为研究背景，建立曲线地段的轨道—隧道—大地三维有限元模型，同时考虑竖向和水平向轮轨作用力的影响，计算得到了地铁列车通过曲线时诱发的环境振动。计算结果表明:当曲线的半径一定时，地铁在曲线地段运行引起的钢轨、隧道壁和地面振动响应均与列车行驶速度密切相关;曲线地段地面水平向振动加速度级要大于竖向，平均高出5 dB;水平向和竖向振动加速度级均表现出随着与隧道中心线间距离的增加而呈波动性衰减特性，频率越高振动加速度级衰减的速度越快;环境振动在衰减过程中都会出现放大区，竖向和水平向的振动放大区出现的位置有所不同，但振动放大区的主频差别不大。

地铁 环境振动 有限元 曲线段

地铁交通以其运量大、速度快、安全可靠、运行准时等特点，成为解决城市交通的重要手段，同时其运行产生的振动通过隧道土层传到地面和地上的建筑，严重影响人们的工作和生活质量。许多国家和地区诸如日本、美国、德国、比利时等发达国家都制定了相应的规范对其引起的影响限值进行了规定，我国《城市区域环境振动标准》也有相应限值规定，国际上已把振动列为七大环境公害之一，很多专家学者并已开始着手研究振动的污染规律、传播途径与控制方法等问题并取得了一定的成果［1-5］。目前，关于地铁诱发的振动的研究方法主要有3个方面:理论分析、计算机数值模拟及现场实测。但是无论采用何种方法，几乎都是针对地铁列车通过直线地段引起的环境振动，关于曲线地段地面和地上建筑的环境振动研究少之又少，实测数据显示直线段和曲线段的环境振动规律存在很大的差异。直线地段的实测表明，垂向振动水平高出水平向较多，评价环境振动水平时，应以垂直方向的振动为主［6］;而曲线地段仅有的实测表明，在距离隧道中心线50 m范围之内，水平振动强度是竖向振动强度的2～4倍，建议在涉及曲线段地铁的环境评价中应同时考虑竖向振动和水平振动的影响［7］。

南昌科技大楼位于南昌地铁1号线八一广场站与中山路站之间圆曲线地段，半径为400 m，根据《地铁设计规范》，外轨超高为120 mm。本文以南昌地铁1号线南昌科技大楼地段工程为依托，以有限元软件ANSYS为计算平台，建立三维轨道—隧道—大地有限元模型，探究地铁列车行驶在曲线地段时诱发的大地振动规律。

1 数值分析模型

列车运行时产生的轮轨振动通过扣件、轨道板、轨道基础、隧道土层等进而引发地面或者地面建筑物的振动，这是一个极为复杂的动态耦合大系统。要将这个完整振动传递路径包含在一个统一的模型中非常困难，现虽有UM-ANSYS、SIMPACK-ANSYS联合仿真等，但主要用于桥面板或者箱梁这样的简单模型的数值计算，在隧道大地这个庞大的系统中很难实现，而且其精度不甚理想。为了克服上述困难，本文将数值分析模型分成2个子模型:

1)地铁 B型车—轨道子模型。利用多体动力学软件建立B型车，在时域内积分求解得到列车通过时轨道的轮轨作用力，将此作用力作为输入条件施加于下一个子系统。

2)轨道—隧道—大地子模型。将第一个子模型得到的轮轨作用力施加到本模型的轨道上，采用时域内的Newmark逐步数值积分法得到体系在计算过程中各时刻的运动状态及其变化情况。

1.1 列车—轨道子模型

列车—轨道子模型求解的结果直接影响到整体的求解质量。本文利用成熟的商业动力学软件SIMPACK建立B型车，基于三角基数法随机生成美国六级水平、高低不平顺谱作为轮轨激励，通过频域法导入列车—轨道模型，导入方法参考文献［8］，B型列车参数见文献［9］，钢轨为60 kg/m轨(忽略其变形，按刚体考虑)，轮对采用LM车轮踏面，列车按最高设计速度50～80 km/h行驶，而根据《地铁设计规范》推荐的轨道曲线超高公式:h=11.8Vc2/R，可得到以120 mm为平衡超高对应的行驶速度为63.78 km/h。

1.2 轨道—大地—隧道子模型

轨道—隧道模型见图1。在有限元模型中，扣件用弹簧单元模拟，扣件间距按实际情况考虑，轨道板下的CA砂浆考虑其总刚度和阻尼，将其等效为均布的弹簧阻尼系统，用 Combin 14单元模拟;土体和轨道板，轨道基础等均按8节点实体单元Solid45考虑，钢轨用空间梁单元Beam188模拟。

1.3 边界的处理及土层参数的选取

三维轨道—隧道—大地有限元模型的边界如果不作任何处理会引起边界上发生波的反射造成计算失真。黏弹性人工边界克服了黏性边界引起的低频漂移，具有良好的高频和低频稳定性，故本文采用黏弹性人工边界对有限元模型的边界域进行处理。为便于黏弹性边界在有限元软件中的应用，本文用等效黏弹性人工边界单元来替换空间分布的弹簧阻尼系统，具体做法是在已建立的三维有限元模型的边界上沿边界面法向延伸一层与土体单元厚度相等的实体单元，并将其外层节点全约束［10-11］。

图1 隧道及轨道模型

土层参数来源于南昌地铁1号线地质报告中南昌科技大楼勘探点数据，具体参数见表1。

表1 科技楼勘探点的土层参数

2 计算结果分析

本文评价地面受地铁交通引起环境振动影响时，竖向指模型中垂直于地面的Y向，水平向指垂直于轨道的X向。文中的振动水平、振动加速度除特别说明外，均指竖直方向和水平方向振动。振动加速度级VL =20lg(arms/a0)，VL为振动加速度级，dB;arms为加速度有效值，m/s2;a0=1×10－6m/s2，为基准加速度。

2.1 轨道的挠度

整个分析过程采用全瞬态的分析方法，计算的总时间由地铁列车的速度和轨道模型的长度来确定，积分时间步长为0.005 s，图2—图5分别为列车以50，70 km/h车速经过隧道时内轨、外轨的竖向挠度和水平向挠度。

轨道挠度分析表明:无论在水平方向还是竖向，当V＜63.78 km/h时，内轨的挠度要大于外轨的挠度，当V＞63.78 km/h时，外轨的挠度要大于内轨的挠度;轨道竖向挠度的大小跟列车的速度有关，随着行驶速度的增大而增大，轨道的水平向挠度与平衡超高对应的速度相关，与平衡超高速度差值越大，挠度越大。

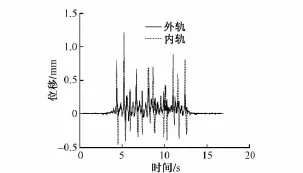
图2 50 km/h水平向挠度

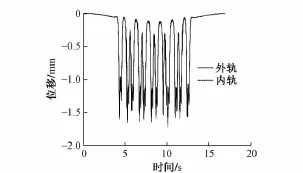
图3 50 km/h竖向挠度

图4 70 km/h水平向挠度

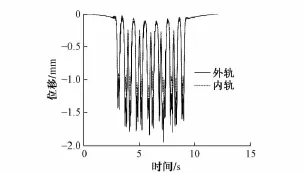
图5 70 km/h竖向挠度

2.2 隧道壁振动加速度

取右线隧道壁上一点进行瞬态分析，图6、图7为在不同速度这一敏感点的加速度时程。

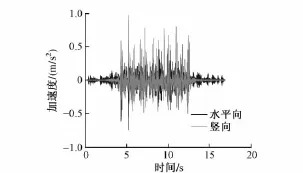
图6 50 km/h时加速度时程

加速度分析表明:当V≤60 km/h时，隧道壁的水平向振动加速度均要小于竖向振动加速度，V≥70 km/h时，竖向振动加速度要小于水平振动加速度;水平向振动加速度和竖向加速度随着速度的增大而增大，且列车行驶速度越高，加速度增加得越快。

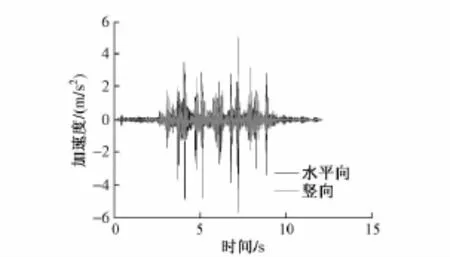
图7 70 km/h时加速度时程

2.3 地面振动的衰减

为了清晰地显现单个频率振动加速度振级随隧道中心线间距离的增加而衰减的特性，本文选取1/3倍频程频带中心频率为10，20，31.5，40，50 Hz，绘制中线频率振动加速度振级随着隧道中心线间距离变化而变化的曲线，如图8、图9所示。

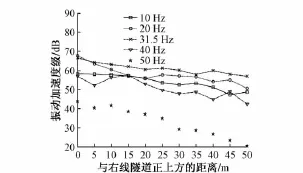
图8 水平向振动衰减

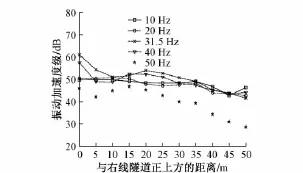
图9 竖向振动衰减

由图8、图9可以发现:水平向的振动加速度级要大于竖向，平均高出5 dB，故在小半径地铁线路地面水平向的振动不能忽略，反而应该更加重视;无论在水平向还是竖向，所有中心频率处的振动加速度级均表现出随着与隧道中心线间距离的增加而呈波动性衰减的特性;频率越高，振动加速度级衰减的速度越快;在竖向，中心频率31.5 Hz和40.0 Hz的振动在距离右线隧道中心线20 m处振动加速度级不降反增，出现振动反弹现象，中心频率为50 Hz的振动放大区出现在15 m处;而在水平向，中心频率40 Hz的振动在15 m处出现放大，50 Hz的振动比40 Hz的振动放大区有所提前，在距右线隧道中心线10 m的位置。故竖向和水平向的振动放大区出现的位置有所不同，但振动放大区的主频差别不大。

3 结论

1)无论在水平向还是竖向，当行车速度小于平衡超高速度时，内轨的挠度要大于外轨的挠度，当行车速度大于平衡超高速度时，外轨的挠度要大于内轨的挠度;轨道竖向挠度随着行驶速度的增大而增大，轨道的水平向挠度与平衡超高对应的速度有关，与平衡速度差值越大挠度越大;外轨的受力方向始终不变，而内轨的受力方向随着速度的增大而趋于稳定。

2)当V≤60 km/h时，隧道壁的水平向振动加速度均要小于竖向振动加速度;V≥70 km/h时，竖向振动加速度要小于水平向振动加速度;水平向振动加速度和竖向加速度随着速度的增大而增大，且列车行驶速度越高，加速度增加得越快。

3)地面上水平向的振动加速度级要大于竖向，平均高出5 dB，故在小半径地铁线路地面水平向的振动不能忽略，反而应该更加重视。无论水平向还是竖向振动，所有中心频率处的振动加速度级均表现出随着与隧道中心线间距离的增加而呈波动性衰减的特性，频率越高，振动加速度级衰减的速度越快。

4)水平向和竖向振动在随着距离衰减过程中都会出现振动放大区，水平向和竖向的振动放大区出现的位置有所不同，但振动放大区的主频差别不大。

［1］丁德云，刘维宁，李克飞，等．地铁运营引起的环境低频振动传播特征试验研究［J］．中国铁道科学，2011，32(2):20-26．

［2］张玉娥，牛润明，朱英磊．地铁列车振动响应分析及控制方法［J］．铁道建筑，2006(5):95-99．

［3］徐新玉．轨道交通系统诱发环境问题及其防控对策研究［J］．铁道建筑，2012(10):154-157．

［4］楼梦麟，贾旭鹏，俞洁勤．地铁运行引起的地面振动实测与传播规律分析［J］．防灾减灾工程学报，2009，29(3):282-288．

［5］韦红亮，雷晓燕，吕绍棣．列车引发地面振动的现场测试及数值分析［J］．环境污染与防治，2008，30(9):17-22．

［6］聂晗，闫维明，任珉，等．地铁交通诱发邻近建筑物振动的实测与分析［J］．铁道科学与工程学报，2008，5(1):51-58．

［7］袁扬，刘维宁，刘卫丰．基于现场测试的曲线段地铁地面振动传播规律［J］．中国铁道科学，2012，33(4):133-138．

［8］赵华伟．客车整车空气悬架多体动力学建模与仿真研究［D］．镇江:江苏大学，2010．

［9］赵雷．B型城市轨道交通车辆转向架低动力作用仿真研究［D］．北京:北京交通大学，2010．

［10］雷文军，魏德敏．无限域地基有限元分析的简化粘弹性边界［J］．地震工程与工程振动，2005，25(3):110-114．

［11］谷音，刘晶波，杜义欣．三维一致粘弹性人工边界及等效粘弹性边界单元［J］．工程力学，2007，24(12):31-37．

Exploring on regularity of ground vibration induced by metro train running at curved section

ZHANG Yan
(School of Civil Engineering and Architecture，East China Jiaotong University，Nanchang Jiangxi 330013，China)

T aking the construction of Nanchang M etro Line 1 as the research background，the track-tunnel-soil three dimensional finite element models of curve sections was established and the induced environmental vibration were calculated when subway train passes the curve section by considering the effects of vertical and horizontal wheel-rail force．T he results showed that the vibration response of rail，tunnel wall and ground caused by curve section subway operation are closely correlated with the train speed when the curve radius is a constant，the horizontal vibration acceleration level is higher than the vertical one on curve section ground and the average value is greater than 5 dB，the horizontal and vertical vibration acceleration level has characteristics of wave attenuation with the increase of the distance from tunnel center line，both vibration acceleration levels decay faster with the higher frequency，there will be amplification area in the attenuation process of environment vibration，the position of vertical and horizontal vibration amplification area is different，but the main frequency of vibration amplification area has little difference．

Subway;Environment vibration;Finite element method;Curve section

TB533+．2

:ADOI:10．3969/j．issn．1003-1995．2015．08．23

(责任审编 孟庆伶)

2015-01-05;

:2015-03-26

国家自然科学基金项目(51268014);江西省高等学校科技落地计划项目(2024)

张燕(1974— )，女，贵州遵义人，副教授，硕士。

1003-1995(2015)08-0076-04