地下水位变化对地铁车站主体结构的影响研究

王志杰，何晟亚

(西南交通大学 交通隧道工程教育部重点实验室，四川 成都 610031)

地下水位变化对地铁车站主体结构的影响研究

王志杰，何晟亚

(西南交通大学 交通隧道工程教育部重点实验室，四川 成都 610031)

为了研究地下水位对地铁车站主体结构的影响，利用ANSYS数值模拟计算在基本荷载组合情况下，不同地下水位的地铁车站主体结构的最大内力值和偏心距。通过比较分析，可以得到不同的地下水位情况下顶板、中板、底板以及侧墙的轴力和弯矩变化小，但是中板的偏心距在地下水位距地表10 m，在顶板以下6 m时，有一个最大峰值。虽然地下水位的变化对地铁车站主体结构的影响小，但是仍需对底层中柱底部进行加固。

地下水位 车站主体结构 数值模拟 最大内力值 偏心距

随着我国经济的高速发展，很多城市都开始进行地铁建设。地铁建设之初，需要开展一些基础性研究工作，例如计算模型的确定，荷载的确定，施工工法的确定和地下水位变化对地铁车站的影响等等。而地下水位的变化，可以由多种原因产生，其中包括季节性降雨，过量使用地下水等等［1-5］。季节性降雨会使地下水位在某段时期上升，而过量使用地下水，则会使地下水位下降。通过对国内外案例的分析，地下水位的下降将会引起地表沉降;而地下水位的上升，将会引起地下结构的上浮、结构的腐蚀、渗水和开裂等等［6］。无论是地下水位的上升和下降，都会引起结构受力的变化，从而引起主体结构内力和偏心距的变化［7］。此内力和偏心距的变化规律以及是否影响地铁车站主体结构安全，是一个值得研究的问题。

地下结构的计算大体可以分为两类，一类是荷载结构模型，另一类是地层结构模型。针对不同的情况，选用不同的模型进行计算。由于地铁车站位于城市中，其埋深较浅且有时会采用明挖法［8］，考虑到结构被动地承受围岩松动所产生的荷载，地铁车站上覆的土层荷载、底板荷载以及侧向荷载都可以确定，所以对此情况采用荷载结构模型。

1 工程概况

某地铁车站处于砂卵石地层中，结构为两层双等跨单柱形式。由于环境条件允许，所以采用明挖法施工。主体结构采用强度等级为C30的钢筋混凝土，保护层厚度为 60 mm。车站主体结构底板埋深为15.25 m，顶板埋深为4 m，其结构每跨为9.05 m，负一层高度为4.90 m，负二层高度为6.35 m。具体的土层参数见表1。由于地下水位的变化，可以将工况分为11个，地下水位分别为 1，2，3，4，5，6，8，10，12，14，16 m。不同工况下地铁车站设计横断面示意如图1。

表1 土层参数

2 荷载组合计算

地铁车站主体结构荷载组合分为两类，分别是基本荷载组合和标准荷载组合。对于地下水位变化引起的主体结构内力的变化规律，可以选取在基本荷载组合下的地下结构进行研究。根据《工程结构可靠性设计统一标准》的规定进行相应的计算。其中基本荷载组合的计算公式为

图1 不同工况下地铁车站设计横断面示意

式中:SGik为永久作用标准值中的第 i个效应;SP为有关代表值的预应力作用效应;SQ1k为第1个可变作用(主导可变作用)标准值的效应;SQjk为可变作用标准值中的第 j个效应;γGi为永久作用中第 i个的分项系数;γP为预应力作用的分项系数;γQ1为第1个可变作用(主导可变作用)的分项系数;γL1，γLj为第1个和第 j个考虑结构设计使用年限的荷载调整系数，对设计使用年限与设计基准期相同的结构，应取γL=1，房屋建筑的设计使用年限为100年时应取该系数为1.1。γQj为可变作用中的第 j个分项系数;ψcj为可变作用中的第j个组合系数。

由以上公式可以计算出11个工况的基本荷载组合，见表2。

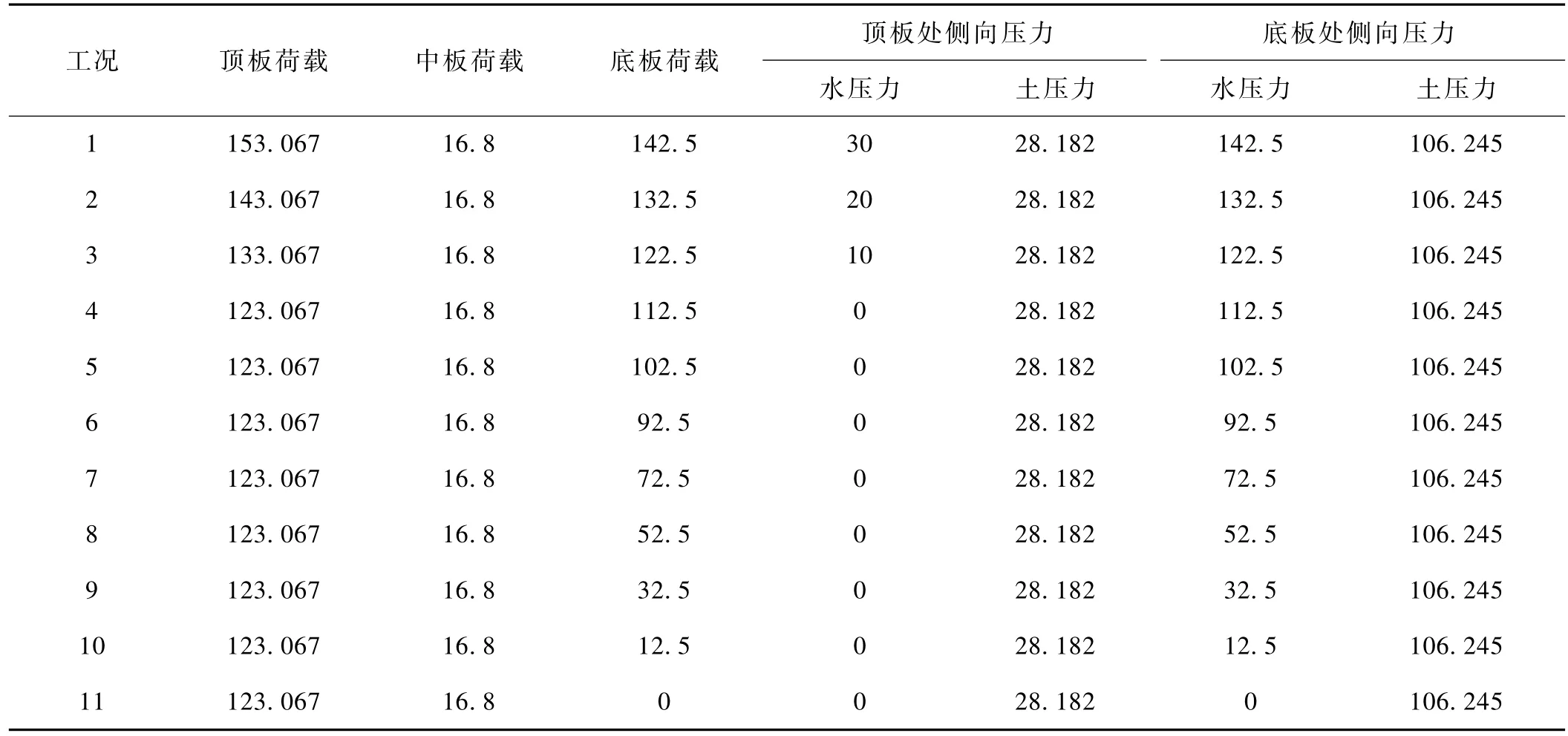
表2 11个工况中主体结构的基本荷载组合 kPa

3 数值模拟分析

3.1 ANSYS数值模型

利用ANSYS对本车站进行主体结构的数值模拟计算，首先采用荷载结构模型进行建模。利用Link10单元来代替地基反力，并设定该单元仅受压，计算中不考虑其受拉。另外，由于本模型与荷载组合均为正对称，理论上中柱处没有水平位移，所以在中柱的底端施加一个水平方向的约束。为了使模型的计算精度提高，以每个单元0.5 m进行划分，建模后模型的单元数为270(其中包括了地基弹簧单元)，网格节点数为267。

3.2 结果分析

在11个工况中，地铁车站在基本荷载组合情况下的各部分轴力最大值的变化趋势见图2，各个工况中各部分弯矩最大值的变化趋势见图3，各个工况中各部分偏心距变化趋势见图4。在ANSYS计算中，所得到的弯矩图与轴力图均呈正对称，而剪力图呈反对称，此与理论一致。由图2—图4可知:

1)在地下水位变化的情况下，地铁车站主体结构的最大轴力和最大弯矩出现的位置均没有发生变化。最大轴力发生在负二层中柱底部，而最大弯矩发生在负二层底板与中柱底部连接处。

2)随着地下水位的下降，顶板轴力的最大值没有太大的变化，基本处于稳定状态;中板轴力的最大值缓慢增加，在工况8之后维持稳定;底板轴力的最大值持续缓慢增大。侧墙的轴力最大值在工况4之前持续增加，但在工况4之后基本没有变化，保持稳定。

图2 轴力最大值的变化趋势

图3 弯矩最大值的变化趋势

图4 偏心距的变化趋势

3)随着地下水位的下降，顶板弯矩的最大值先增大，后保持稳定，基本没有变化;中板弯矩的最大值基本保持稳定，没有太大的变化;底板弯矩的最大值先减小，后保持基本稳定。侧墙弯矩的最大值在工况8之前缓慢增加，但在工况8之后稳定不变。

4)随着地下水位的下降，顶板的偏心距保持稳定，没有明显的变化;中板的偏心距逐渐增加，特别是在工况8时，达到最大峰值，之后在工况9，10，11时稳定平缓，但是总体上，偏心距还是增加了;底板的偏心距缓慢增加。侧墙的偏心距基本保持不变，相对各部分而言，其偏心距最小。

5)当地下水位越靠近中板，中板的偏心距就越大，在工况8时达到一个最大峰值。

4 结论

采用ANSYS数值模拟分析在地下水位变化的情况下地铁车站主体结构内力以及偏心距的变化规律，通过对比内力与偏心距数据可以得到以下结论:

1)随着地下水位的变化，地铁车站主体结构的受力也发生了变化，从而导致了内力也发生变化，但是这种变化较为稳定。

2)随着地下水位的变化，轴力和弯矩的波动都很小，基本上保持缓慢上升或者平稳的趋势。但是对于中板的偏心距而言，其变化较大，产生了一个较大的峰值。

3)在施工过程中，由于轴力和弯矩的最大值均发生在地铁车站底层的中柱底部，所以要加大该处的刚度，尽量减小该处的轴力和弯矩。

4)由于轴力与弯矩的变化并不大，所以地下水位的变化对地铁车站主体结构的影响小。

［1］邓睿．地下水位变化对路基稳定性影响分析［J］．铁道工程学报，2014(1):37-41．

［2］谭新平，方文俊，王小秋．西安市地下水位变化对工程的影响［J］．陕西建筑，2010(7):55-59．

［3］成璐，许模，毛邦燕．成都地铁2号线对地下水的影响评价［J］．路基工程，2009(1):128-129．

［4］毛邦燕，许模，唐万春，等．地铁建设中地下水与环境岩土体相互作用研究［J］．人民长江，2009，40(16):49-52．

［5］杨晓婷，张徽，王文科，等．地下工程建设对城市地下水环境的影响［J］．铁道工程学报，2008(11):6-10．

［6］董军，宋文杰，崔玉萍，等．地下水与隧道施工对既有地铁车站结构影响研究［J］．施工技术，2013，42(增):281-285．

［7］罗富荣，刘赪炜，韩煊．地下水水位上升对地铁隧道结构的影响［J］．中国铁道科学，2011，32(1):81-85．

［8］刘魁刚，王文正，裴书锋．砂卵石地层浅埋暗挖法快速施工技术［J］．现代隧道技术，2011，48(5):115-120．

(责任审编 赵其文)

U231+.4

:ADOI:10．3969/j．issn．1003-1995．2015．08．18

2014-07-10;

:2015-05-18

中央高校基本科研业务费专项资金资助项目(SWJTU11ZT33)

王志杰(1964— )，男，山西万荣人，教授。

1003-1995(2015)08-0061-03