基于序lasso的时间序列分析方法

王金甲，陈　春，洪文学(.燕山大学信息科学与工程学院，河北秦皇岛066004;2.燕山大学电气工程学院，河北秦皇岛066004;3.东北大学秦皇岛分校大数据可视化分析技术中心，河北秦皇岛066004)

基于序lasso的时间序列分析方法

王金甲1，陈春1，洪文学2，3，*
(1.燕山大学信息科学与工程学院，河北秦皇岛066004;
2.燕山大学电气工程学院，河北秦皇岛066004;
3.东北大学秦皇岛分校大数据可视化分析技术中心，河北秦皇岛066004)

摘要:传统的lasso法因其解的稀疏性、变量选择的稳定性被广泛应用在高维、复杂、多变的大数据的降维及分类中，但在处理时序大数据时，lasso法因不考虑变量的时序关系而受限制。鉴于这一缺点，本文在处理时序数据时采用序lasso方法。序lasso将不同特征的不同时间点的数据作为输入变量，能够有效地估计出每个特征最合适的时滞间隔，它的优点是在恢复真实系数上消除了尾部的波动性。基于实际的时序数据上的实验结果证明了本文的模型和算法。

关键词:时序大数据;序lasso;块坐标下降;保序回归

0　引言

随着移动互联网、物联网和云计算技术的迅速发展，各个领域都出现了大规模的数据增长。在过去的两年中，每天都会产生大概2.5×109个字节的数据［1］。大数据这一术语正是产生在数据爆炸增长的背景下。李国杰院士等［2］对大数据的定义为:大数据是指无法在可容忍的时间内用传统的IT技术和软硬件工具对其进行感知、获取、管理、处理和服务的数据集合。

由于大数据存在复杂、高维、多变等特性，造

成存储分析挖掘等多个环节的困难［3］。传统的非线性机器学习算法诸如压缩最近邻、近邻等方法［4］由于计算量大，算法的收敛速度慢等缺点只适用于较小规模的数据集。1996年Robert Tibshirani提出了一种新的变量选择方法(least absolute shrinkage and selection operator，lasso)［5］。该方法用模型系数的1范数作为惩罚来压缩模型系数，使绝对值较小的系数自动压缩为0，从而同时实现显著性变量选择和对应参数的估计，很好地克服了传统方法在选择特征上的不足［6］。lasso方法不仅能够准确地选择出重要特征，而且具有特征选择的稳定性，这些优点使得它在生物医学、光学等背景下的大数据集上得到广泛的应用［7］。此外，将lasso方法运用到p阶自回归模型AR(p)的时序大数据上，就可以将模型的定阶和参数估计这两个步骤合二为一，简化计算过程，提高计算效率［8］。但在处理时序大数据时，lasso方法并不考虑数据的时序关系，这会造成数据潜在信息的浪费，也可能对后续的分析产生误导［9］。因此本文采用序lasso(ordered lasso)方法分析时序数据，序lasso方法在恢复真实系数上能够有效地消除尾部的波动性，估计出每个特征最合适的时滞间隔。

1　基于序lasso的大数据处理流程

整个大数据处理流程如图1所示。经数据源获取的数据，因为其数据结构不同，用特殊方法进行数据处理和集成，将其转变为统一标准的数据格式方便以后对其进行处理，然后用合适的数据分析方法对其进行处理分析，并将分析的结果利用可视化等技术展现给用户。在整个处理过程中，数据分析是最核心的部分，因为在数据分析的过程中会发现数据的价值所在。经过数据的处理与集成后，所得的数据便成为数据分析的原始数据，根据所需数据的应用需求对数据进行进一步的处理和分析。传统的数据处理分析方法有数据挖掘、机器学习、智能算法、统计分析等。

图1　大数据处理基本流程Fig.1　Basic framework of big data processing

2　lasso方法

2.1基本原理及算法

假定有N对观测数据(xi，yi)，其中i = 1，2，…，N，xi= (xi1，xi2，…，xip)是p维的特征向量，yi是相应的响应向量值。并且假定xij是标准化的，即有。线性模型在lasso罚下的参数估计可以描述为

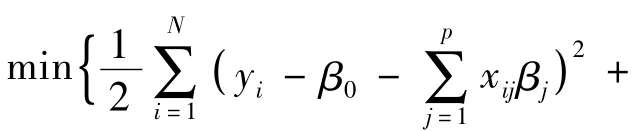
本文运用坐标下降法针对固定的λ值求解式(1)。假设已估计出β槇0和β槇l(l≠j)，仅对βj进行部分优化，计算βj=β槇j处的梯度，要求β槇j≠0，否则梯度不存在。记分3种情况(βj＞0，βj＜0，βj= 0)分别对式(2)求导，求其最小值，结果总结如下:

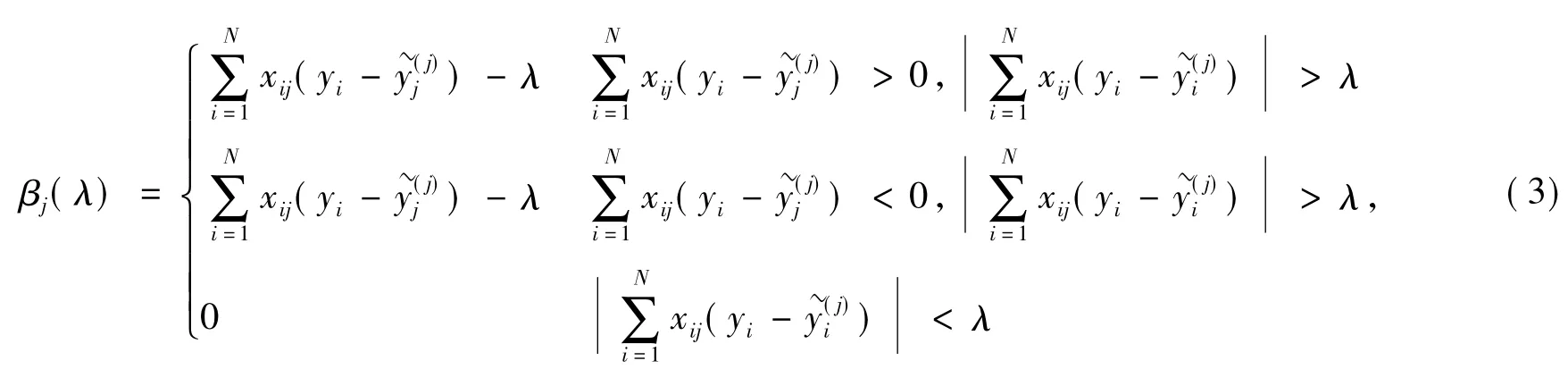
式(4)即为lasso罚的线性回归模型参数估计的迭代更新公式。

2.2lasso在时序大数据上的应用

线性滚动预测模型的主要思路是利用近期数据的线性形式来预测数据变化趋势。在这儿假定数据形式{ yt，xt1，…，xtp}，其中t = 1，2，…，N。记录的是在N个不同的时间点的每个预测变量的值及输出结果。考虑一个最大时延为K的时滞回归模型，即K阶滚动线性预测模型: yt=β0+，其中，E(εi) = 0，Var(εi) = σ2。在该模型的基础上加罚:

为了解决这一问题，建立一个大小为N×(Kp)的特征矩阵Z，特征矩阵Z每一行的形式为{ xt-1，1，xt-2，1，…，xt-K，1xt-1，2，xt-2，2，…，xt-K，2…xt-1，p，xt-2，p，…，xt-k，p}。矩阵Z有N行这样的值。根据新构建的特征矩阵Z及响应向量y，运用式(4)求解滚动预测模型的参数值。

3　序lasso方法

3.1基本原理

在特征存在自然顺序的问题中，在lasso罚中再添加单调非递增约束条件是很有必要的，即

式(6)即为本文介绍的序lasso方法(Ordered lasso)。然而，由于顺序约束条件的加入使得这一问题非凸。为求解式(6)，将每一个βj都写成如下形式:βj=β+j－βj，且β+j，βj≥0。正负组件的使用将非凸问题(6)转换为凸问题:

式(7)可用一阶广义梯度算法求解。用保序回归中的PAVA算法作为它的近邻算子即可。

3.2算法细节

为求解方便，假定截距^β0= 0。令X是N×p的数据矩阵，y是长度为N的响应向量。首先考虑如下问题:

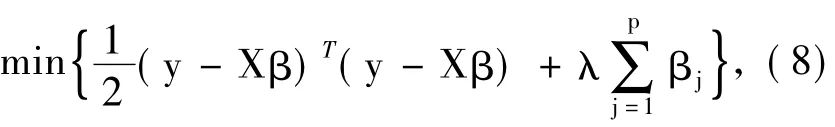
s.t.β1≥β2≥…≥βp≥0，将带有单调非递增约束条件的式(7)记作minf(β) + h(β)，其中，f(β)

‖C(β)，‖是一个指示函数，C是由{β∈Rp|β1≥β2≥…≥βp≥0}给定的凸集。采用一阶广义梯度算法，可以得到β的迭代更新公式为

其中，L是Lipschitz系数，γ＞0是步长，要求它在每一步的更新过程中，目标函数都是递减的。下面接着计算h(β)的近邻映射，即

将式(10)转化为以下问题:

采用经典的保序回归算法(Pool Adjacent Violators Algorithm，PAVA)得到保序回归{ yi－λ}的解{i} = {λi}，那么{λi.‖(λi＞0) }是式(11)的解。因此式(10)的解为

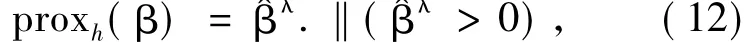
将该式应用到一阶广义梯度梯度算法中，那么求解式(8)的更新β的步骤为

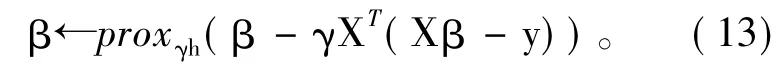
以上过程完成了单独的β+(β－)的求解，为了求解式(7)，需要把每一个预测变量Xij扩展成x*ij=－xij，那么有xijβj= xijβj++ x*ijβj－，定义扩展变量对(β+，β－)，并把近邻算子(13)式分别运用到X、X*来得到最小的扩展变量对(+，－)。

3.3在时序大数据上的应用

仍假定数据形式{ yt，xt1，…，xtp}，其中t = 1，2，…，N。令βkj=βk+j－βk－

j，求解下式:

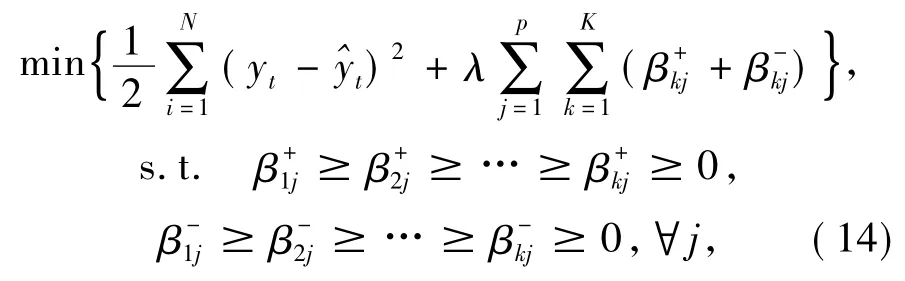
同2.2节类似，仍然建立矩阵Z，并将每一行的数据分为p块，每一块对应单个预测变量延迟1，2，…，K个时间单位的值。故Z 每一行的形式仍然扩展每一个预测变量xt-K，j，令x*t-k，j=－xt-k，j。选择一个有效的最大延时K，令每个预测变量在K个时间点之外的系数为0。用块坐标下降法［10］求解式(14)。

4　实验结果与分析

在自回归时间序列模型中，最大延时为k时，可从yt-1，yt-2，…，yt-k预测yt，这符合滚动预测模型框架。只是回归变量是它自身的不同的时间点的时间序列。这一例子使用公开的sunspot.year数据，它包含了289个观测值，代表的是从1700年到1988年每年的太阳黑子的数量。该数据的时序图、自相关图、偏相关图分别如图2的(a)～(c)所示，图中蓝色虚线表示置信区间。从图中可以看出，该时间序列的自相关图拖尾，偏相关图截尾，且偏相关图在滞后9阶之后缩至为0，所以初步判定可以使用AR(9)模型。本文中，将lasso、序lasso和传统的AR模型拟合进行了比较，AR拟合的阶数是由最小二乘和AIC计算得到，lasso和序lasso中，假定最大时滞为20，采用10倍交叉验证获得最佳模型。图3给出的是将自回归模型应用到太阳黑子数据上的结果。

从实验结果可以看出，标准的AR拟合得到的是9阶AR模型，序lasso的阶数是10，并能得到一个较好的系数序列。而lasso则因尾部的波动不能确定模型的确切阶数。

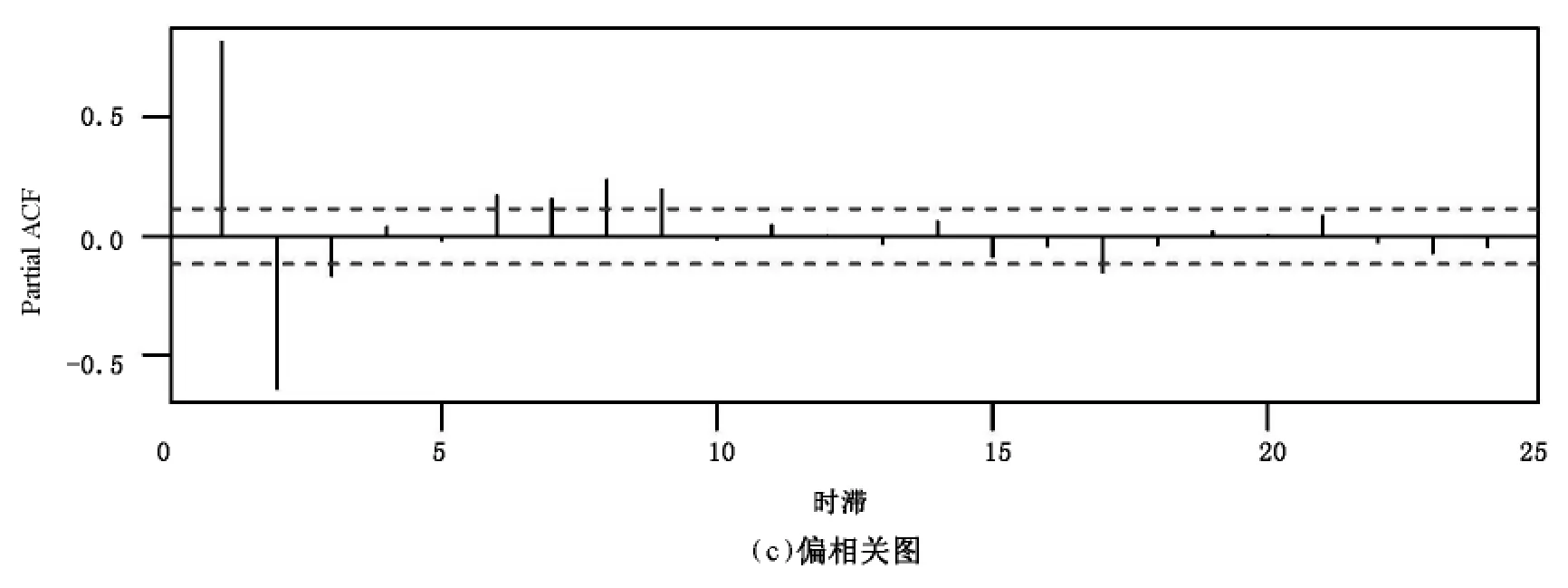
图2　太阳黑子数据示意图Fig.2　Sunspot data sketches

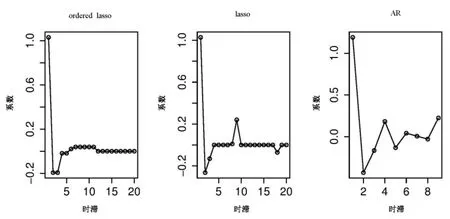
图3　lasso、序lasso、AR模型在太阳黑子上的系数估计Fig.3　Sunspot data: estimated coefficients of the ordered lasso，the lasso and the standard AR fit

5　结论

lasso方法不仅能够准确地选择出重要特征，而且具有特征选择的稳定性，这些优点使得它广泛应用在大数据的降维及分类中。但在处理时序大数据时，lasso方法并不考虑数据的时序关系，会造成数据潜在信息的浪费，也可能对后续的分析产生误导。采用序lasso方法处理时序数据，能有效地改进lasso法的不足。本文将lasso、序lasso方法应用到太阳黑子数据上，从实验结果可以看出，序lasso和lasso在自回归模型上能取得和标准的AR模型拟合相近的性能，而序lasso更因其尾部的稳定性胜于lasso。这也充分证明了将序lasso应用到基于时滞回归模型的预测问题上是可行的，为将来在金融问题、临床医学问题等大数据的处理上提供了可能。

参考文献

［1］Wu Xindong.Data mining with big data［J］.IEEE Transactionss on Knowledge and Data Engineering，2014，26(1) : 97-98.

［2］李国杰，程学旗.大数据研究:未来科技及经济社会发展的重大战略领域-大数据的研究现状与科学思考［J］.中国科学院院刊，2012，27(6) : 647-657.

［3］王元卓，靳晓龙，程学旗.网络大数据:现状与展望［J］.计算机学报，2013，36(6) : 1126-1127.

［4］Muja M.Lowe D G.Scalable nearest neighbor algorithms for high dimensional data［J］.IEEE Transactions on Pattern Analysis and Machine Intelligence，2014，36(11) : 2227-2230.

［5］Robert Tibshirani.Regression shrinkage and selection via the Lasso ［J］.Journal of the Royal Statistical Society，Series B(statistical methodology)，1996，58(1) : 267-288.

［6］Yamada M.High-dimensional feature selection by feature-wise kernelized lasso［J］.Neural Computation，2014，26(1) : 185-187.

［7］Liu Fayao.Multiple kernel learning in the primal for multimodal alzheimer's disease Classification［J］.Journal of Biomedical and Health Informattics，2014，18(3) : 984-985.

［8］谢仪，高雪，景英川.基于Lasso及Adaptive Lasso的AR(p)模型定阶及参数估计［J］.浙江工业大学学报，2014，42 (4) : 463-465.

［9］姜高霞，王文剑.时序数据曲线排齐的相关性分析方法［J］.软件学报，2014，25(9) : 2003-2004.

［10］Li Haifeng，Fu Yuli，Hu Rui，et al.Perturbation analysis of greedy block coordinate descent under RIP［J］.IEEE Transactions on Signal Processing Letters，2014，21(5) : 519-520.

Time series analysis method based on ordered lasso

WANG Jin-jia1，CHEN Chun1，HONG Wen-xue2，3
(1.College of Information Science and Engineering，Yanshan University，Qinhuangdao，Hebei 066004，China; 2.College of Electrical Engineering，Yanshan University，Qinhuangdao，Hebei 066004，China; 3.Big Data Visualization Technology Center，Northeastern University at Qinhuangdao，Qinhuangdao，Hebei 066004，China)

Abstract:When doing data mining on high dimensional，complex，and changeable data，it is necessary to reduce the dimension of primal data at first.Traditional lasso method is widely used for reducing the dimensionality and classification because of the sparsity of its solution and the stability of variable selection.However，when dealing with time-series data，it doesn't consider temporal relations of variables，so its application is limited.Given this shortcoming，ordered lasso of handling time-series data is proposed in this paper.The input variables of ordered lasso are the different time points according to different predictors.For each predictor，the ordered lasso can estimate the best suitable time-lag interval.The advantage of ordered lasso in recovering real coefficients is that it can eliminate the fluctuations in the tails.Experimental results on real time-series data have proved ordered lasso method is feasible.

Key words:time-series big data; ordered lasso; block coordinate descent; isotonic regression

作者简介:王金甲(1978-)，男，河南商丘人，博士，副教授，主要研究方向为信号处理和模式识别; *通信作者:洪文学(1953-)，男，黑龙江依安人，教授，博士生导师，主要研究方向为大数据偏序结构理论、复杂概念网络、可视化模式识别和中医工程学，Email: hongwx@ ysu.edu.cn。

基金项目:国家自然科学基金资助项目(61473339) ;中国博士后科学基金资助项目(2014M561202) ;河北省2014年度博士后专项资助项目(B2014010005) ;首批“河北省青年拔尖人才”资助项目

收稿日期:2014-07-05

文章编号:1007-791X(2015) 01-0030-05

DOI:10.3969/j.issn.1007-791X.2015.01.005

文献标识码:A

中图分类号:TP18; TP391