基于散焦的三维显微粒子追踪测速

赵攀杰，王昊利

（中国计量学院 计量测试工程学院，浙江 杭州 310018）

显微散焦数字图像追踪测速技术是在宏观散焦测速技术应用的基础上发展而来的.该散焦理论最初是由 Willert等人［1］提出，之后Pereira等人［2］对散焦光学理论进行了详细的解释，并推导出了相关的几何光学方程式，以此可估算出粒子在三微流场中的位置.Kajitani等人［3－4］对散焦方程式进行了修正，并通过不确定分析建立了三维几何不确定度的模型.Wu等人［5］利用示踪粒子散焦时产生衍射环的特殊图像方式对三维粒子的运动进行了追踪，但该方法得到的粒子图像像散现象严重，误差比较大.Yoon等人［6］成功地将散焦技术用到了微尺度流动的测量中，并针对后台阶结构通道内流体雷诺数Re＝0.025的微流动进行了测量，获得了粒子的运动轨迹和深度可达50μm的三维速度场.Pereira等人［7］基于此技术而设计了一个高速三维显微散焦粒子测速系统，成功地实现了蒸发液滴内流动速度达到1.5mm／s的2μm荧光粒子的三维追踪.Lu等人［8］也用此高速显微粒子测速系统对动态生物细胞运动进行了定量分析.

由于实验中所研究的测试流体是多种多样的，流体的折射率成为了该系统标定的一关键因素.Yoon等人［9］提出了一种新颖的微流体装置，测得的折射率与五种流体样品标准的折射率最大偏差为0.0036（0.24%）.Yoon等人［10］通过实验的方法推算出了流体折射率和相应的标定系数之间的相互关系，减少了不同测试流体需重复标定的工作.此外，除了常用的三孔挡板外，为了克服由于粒子多次曝光造成的图像饱和极限，Tien等人［11］在挡板的每个孔上放置了一个可过滤不同单色光的滤色片.另外，Lin等人［12］提出了一种基于环形孔挡板的散焦技术，该挡板结构光学效率高，是一种很有前景的方法.

本文设计加工了散焦粒子图像测速技术的核心元件三孔挡板（three pinhole mask），搭建了高速显微散焦粒子测速系统，在研究标定和粒子识别方法的基础上，对台阶结构微通道运动轨迹进行了追踪测速.

1 实验系统和微通道

图1给出了高速 Micro－DDPIV／DDPTV系统装置示意图，从图中可以看到三孔挡板的安装位置.该系统是在现有的德国LaVison公司生产的Micro－PIV／PTV系统装置的基础上改造而成.光源采用了波长为532nm，功率为5W的连续激光器（型号为LIF－532－5）.图像采集装置使用了日本生产的MEMRECAM HX－6型CMOS高速相机，最大帧频可达5000帧／s.根据实验装置的实际状况，本文设计的挡板为边缘厚度0.1mm，距挡板边缘间厚度成线性分布的三孔挡板，小孔直径为2mm，过三孔圆心的圆直径为4mm.使用20×0.4倍的显微物镜对微流场中直径为2μm的荧光粒子进行观测，所观测的微流体视场为205μm×205μm×50μm.实验中CMOS相机设定为1000帧／s的扫描速率记录序列图片，图片的规格为640×640pixel.

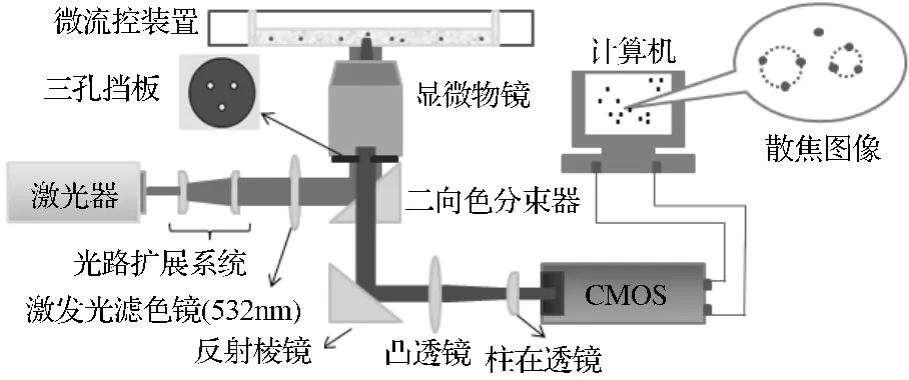
图1 高速Micro－DDPIV／DDPTV系统装置示意图Figure 1 Device diagram of the high speed Micro－DDPIV／DDPTV system

为了验证实验结果的可靠性，设计了倒置台阶结构微通道，如图2.通道由下端的玻璃板和上端的PDMS材料制作而成（图2（a）），其长L和宽w分别为11mm和2mm，进口处深度h1为50μm，出口处深度h2为25μm，两端口水平长度L1和L2均为5.5mm（图2（b））.实验中所配溶液中纯水与荧光粒子液的体积比为2000∶1，注射泵（格兰公司生产）的流量为371.6μl／h，微通道进口处流体的雷诺数Re＝0.1.其中此方形微管的水力直径d＝2wh1／（w＋h1）.

2 散焦测速原理

图3为高速显微散焦粒子测速系统的光路原理简图.从图中可以看到，荧光通过三孔挡板后在CMOS相机图像传感器上形成散焦图像.散焦图像通常为等边三角形构型，其边长和方向由荧光粒子的空间位置决定，而在参考平面（Reference plane）上三个像点聚焦为一点.参考平面内外等距离处（图3中z＞0和z＜0处）粒子的散焦图像所成的等边三角形边长相等但方向相反，即“等大反向”，从而避免了深度歧义的问题.

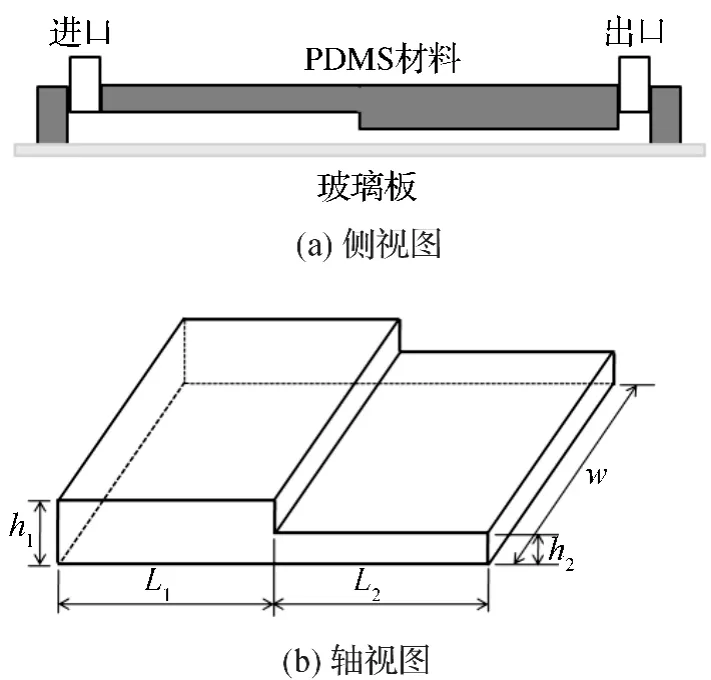
图2 倒置台阶结构微通道示意图Figure 2 Schematic diagram of microchannel for the inverted step

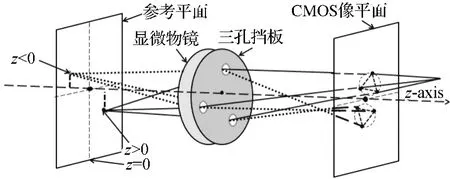
图3 散焦光路系统原理简图Figure 3 Principle diagram of the defocusing optical system

以粒子三角模型散焦像外接圆的直径D和圆心（X，Y）来分别表示粒子的像径及其在水平面的位置.由几何关系，有：

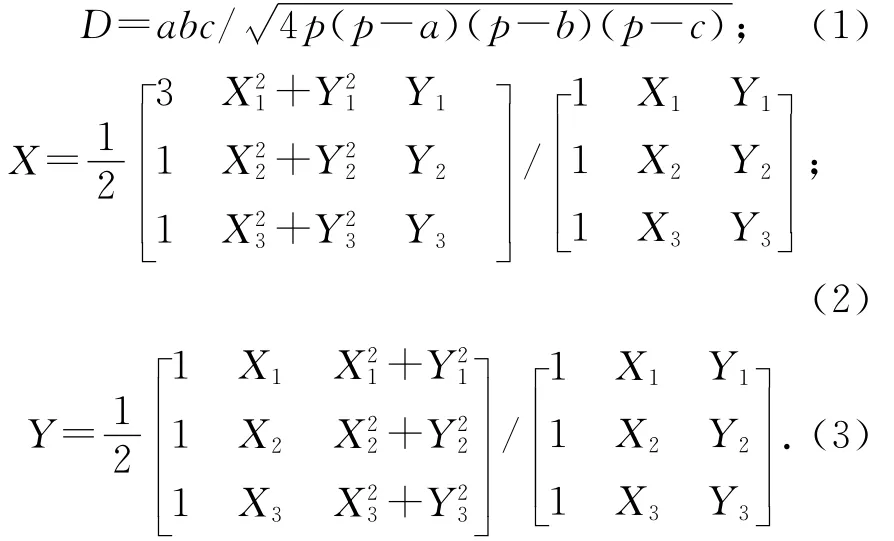
式中：a，b和c—三个像点的间距，p＝（a＋b＋c）／2.（X1，Y1），（X2，Y2）和（X3，Y3）分别为粒子所对应三个像点的质心.

2.1 标定方法

标定方法如图4，荧光粒子固定于上端载玻片下表面，通过精确调整上载玻片的垂向位置，建立垂向坐标与荧光粒子散焦图像几何构型（如三孔距离和方向）之间的关系，获得标定结果.由于实验所用工作流体是多种多样的，为了减少这种重复的标定工作，Yoon等人［10］通过实验的方法推算出了流体折射率和相应的标定系数之间的相互关系.对于不同的流体，根据光路分析可以获得实验流体和标定所用的参考流体之间的标定关系式，见式（4）.

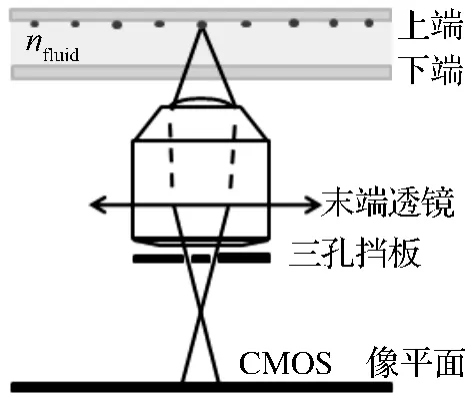
图4 标定原理简图Figure 4 Principle diagram of the calibration

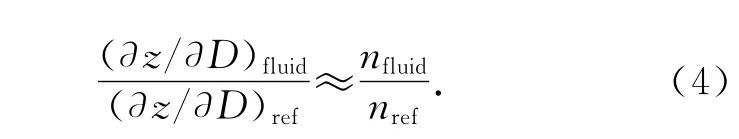
其中：nfluid和nref—实验溶液和参考流体的折射率，（∂z／∂D）fluid和（∂z／∂D）ref为这两种溶液对应的标定系数.而根据Yoon等人［10］的实验结果可以看出，以在空气中标定得到的深度标定系数为参考，将空气换成纯水后，经公式（4）计算出的深度标定系数，与在纯水中标定得到的深度标定系数相比，其误差只有0.013（1.38%）.因此，本实验采用空气作为工作介质进行标定.

基于上述标定原理，本文采用了一类简便易行的方法：将低浓度的荧光粒子溶液沉积在载玻片表面，蒸发后在载玻片上形成固定的荧光粒子，将其作为标定粒子；利用系统自带的高精度三维坐标架对z方向进行精确定位（最小分辨率可达0.1μm），沿深度方向每间隔2μm采集一次粒子散焦图像；建立散焦图像构型特征与深度位置的标定关系式，利用公式（4）完成工作介质空气与水溶液两者相应标定系数的转换，从而实现粒子深度方向位置的标定.

2.2 粒子识别

粒子图像识别采用了Yoon等人［6］提出的相似度理论，其公式见式（5），几何关系如图5所示.其中，向量（r1，r2，r3）和（c1，c2，c3）分别表示参考模式（以标定中颗粒对应的散焦像作参考）和正在识别中的三角形模式.根据图5，建立判别准则进行粒子识别.当S≥0.99时，则认为识别中的三个像斑为粒子对应的三角模式.

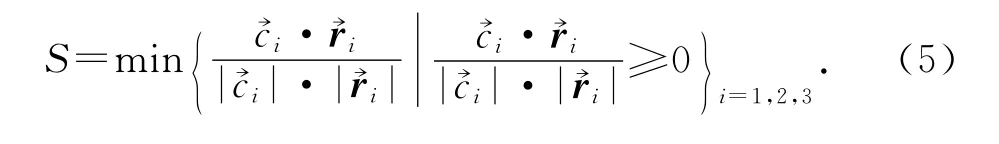
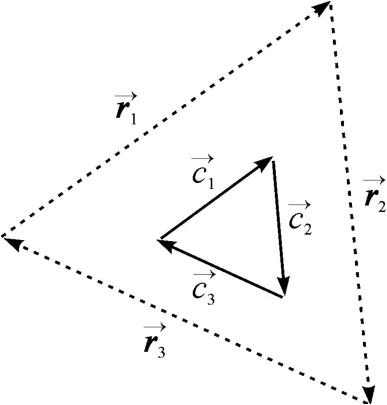
图5 参考的三角形（图中虚线）与识别中的三角形Figure 5 Reference triangle（the dotted line）and the triangle in recognition

3 实验结果及分析

3.1 粒子散焦图像

图6给出了距参考平面一定间距处的散焦粒子图像.其中，第一排为近场（参考平面以内，z＞0）中提取的不同深度处的标定图像，第二排为远场（参考平面以外，z＜0）的结果.从图中可以看出，在远离参考平面的过程中，粒子散焦图像的大小呈现正比例增大的趋势.在z＞0和z＜0方向上距参考平面相同距离的深度处粒子散焦成像基本呈等大反向规律.鉴于粒子距参考平面较远时所成散焦像点易变得模糊，在深度较大的流场中，可同时取近场和远场的散焦图像，并通过这种不同深度处“等大反向”的成像方式来对测量区域进行归类.

3.2 粒子追踪结果

图6 距参考平面一定间距处的散焦粒子图像Figure 6 The defocused particle images with a certain distance from the reference plane

从散焦光路的几何分析中可知，同一深度处不同水平位置的粒子所成的散焦像的大小应是相等的.这里本文取同一深度处11个粒子像径的均值作为该深度处所对应的粒子像径.从图7（a）中可以看出，粒子像径与其对应的深度呈较好的线性关系.然而，根据Pereira等［2］的研究结果，在大深度方向上粒子像径随深度的变化呈现非线性特征.本文研究结果也表明，在离参考平面较近的区域粒子像径随深度表现出弱非线性特征.如图7（b），粒子像径与深度增量之比ΔD／Δz随深度在参考线（图中水平虚线，－1.665）上下浮动，其均方根误差（RMS）为0.1162.

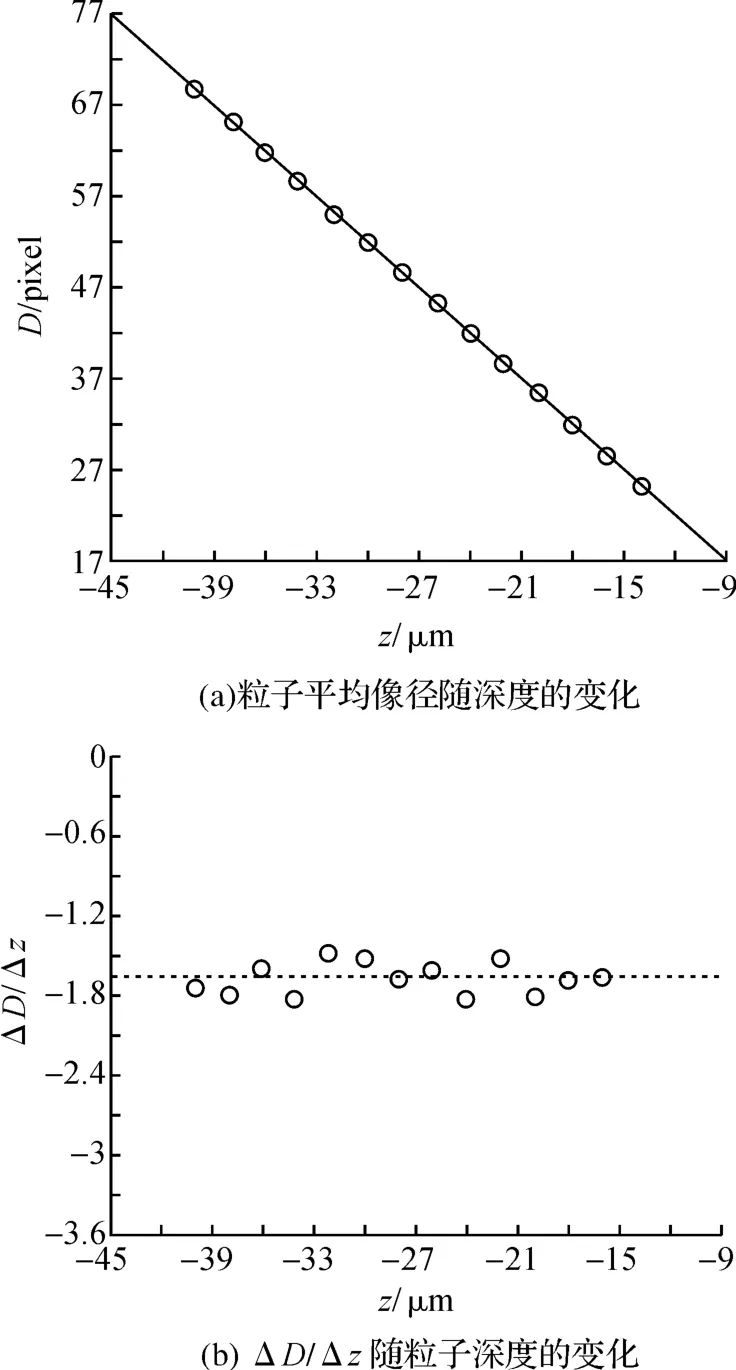
图7 粒子平均像径及ΔD／Δz随粒子深度的变化Figure 7 Changes in average diameter of the particle andΔD／Δz with z positions of the particle

固定粒子散焦图像及其上下左右四端粒子像径随粒子深度的变化如图8.其中，图8（a）给出了上下左右四个位置的粒子图像，图8（b）绘制出这四个位置粒子像径随深度的变化的趋势分布.从图8中可以看出，不同深度下，四个位置像径非常接近，说明同一深度处粒子像径的大小基本不受其水平位置的影响.

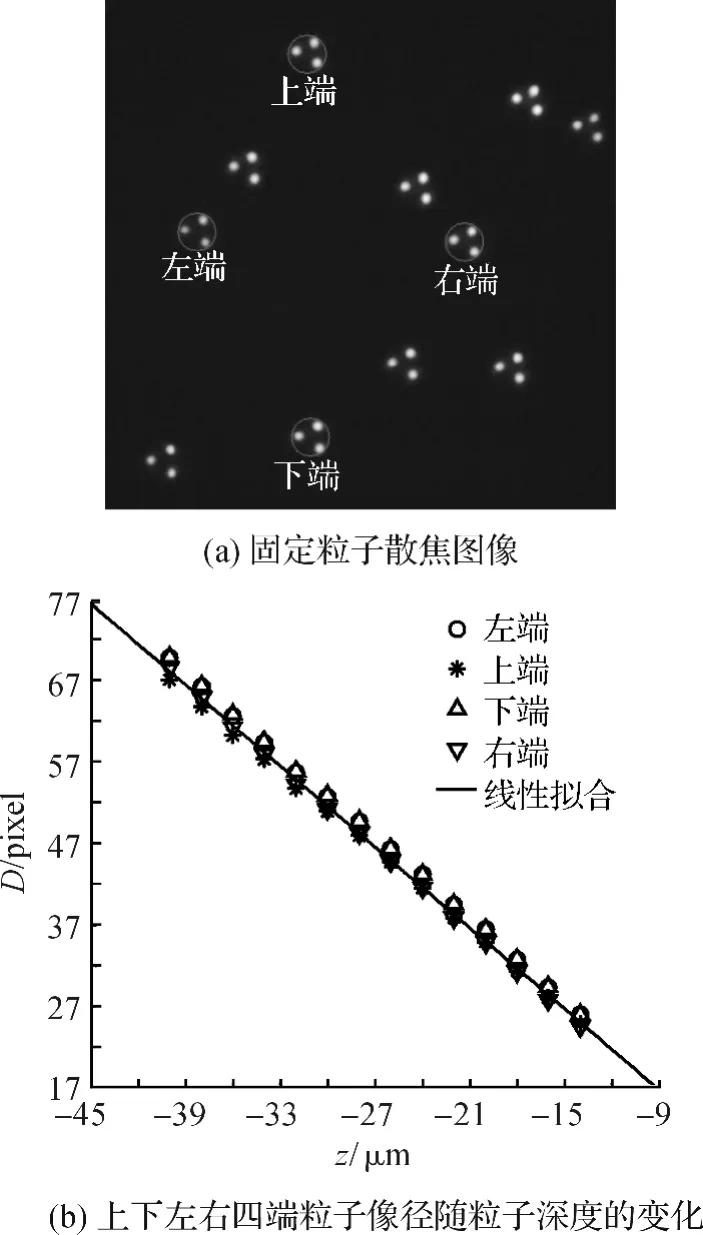
图8 固定粒子散焦图像及上下左右四端粒子像径随粒子深度的变化Figure 8 Focus image of the fixed particles and changes of diameter D according to z positions of the particles at left edge，upper edge，lower edge and right edge.

根据深度方向的标定方法，在参考平面附近的粒子深度z与其像径D之间的关系可写为如下线性方程：

式（6）中：标定系数a＝（∂z／∂D）ref，b—一常量.

通过关系式（4）可以求得在工作流体荧光粒子溶液中进行标定时粒子深度与其像径的关系式如下：

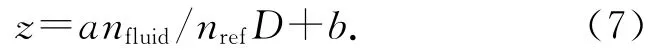
实验中发现：同一粒子不同深度处和同一深度粒子不同水平位置处，粒子的相对位移Δx和Δy均是不同的.由于深度方向上能对粒子的相对位移进行定量分析，粒子相对位移随深度变化呈现出明显的非线性趋势.鉴于固定粒子在玻璃板上是随机分布的，在水平方向上这种定量分析有一定难度，但很显然，粒子的相对位移与粒子的水平位置有关，而实验测量中须尽可能消除这种相对位移（即粒子位置漂移）.为了消除位置漂移，本文采用了多项式补偿函数方法［6］：

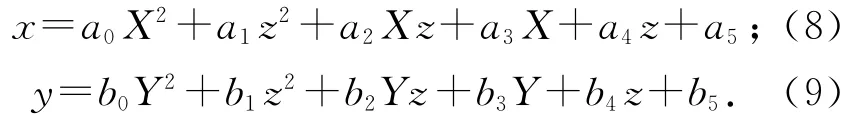
其中：X和Y—粒子在像平面中的坐标位置，z—其实际深度，x和y—其在水平方向上的实际位置.本文利用最小二乘法对不同深度不同水平位置处与粒子三维空间坐标有关的154组数据进行了二元二次多项式的拟合，得到了粒子位置x和y的补偿函数.

图9给出了样品粒子位置x和y补偿前后的情况，这里把粒子在深度方向z＝0处的水平位置（x，y）定义为粒子的参考位置.从图9（a）和（b）中可以看出，经x／y补偿函数修正后粒子的水平位置得到了明显改善，其大小随深度在参考线（图9中过参考点的水平虚线）上下轻微浮动.

图10给出了粒子测量位置x／y／z的误差分析结果.其中，Re为均方根误差RMSE（Root Mean Square Error）.经深度标定函数测得的同一深度处所有粒子的位置与其标定深度的均方根误差Re随标定深度在参考线Rz＝0.4739μm附近变化.而经x／y补偿函数修正后的同一深度处的所有粒子的位置与其各自的水平参考点的均方根误差Re随标定深度分别在参考线Rx＝0.177μm和Ry＝0.2155μm上下轻微变化.由于粒子像径随标定深度的轻微非线性变化和其三维方向分辨率的不同等因素，粒子深度方向的测量误差是其水平方向测量误差的2～3倍.与Pereira［2］及 Yoon［6］等对粒子在深度与水平方向测量误差的比对实验结果一致.

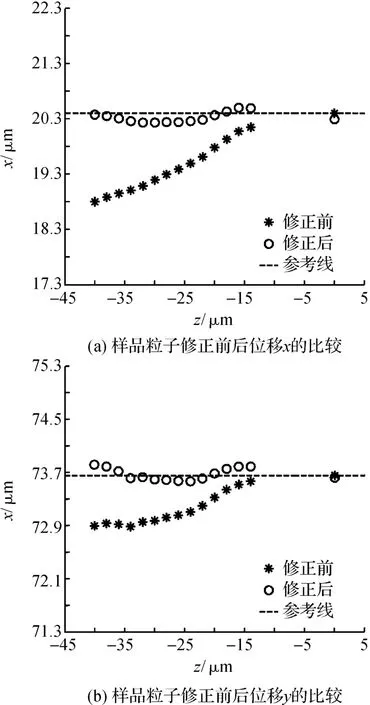
图9 样品粒子修正前后位移x／y的比较Figure 9 Comparisons of the sample between the non－compensated and the compensated x／ypositions

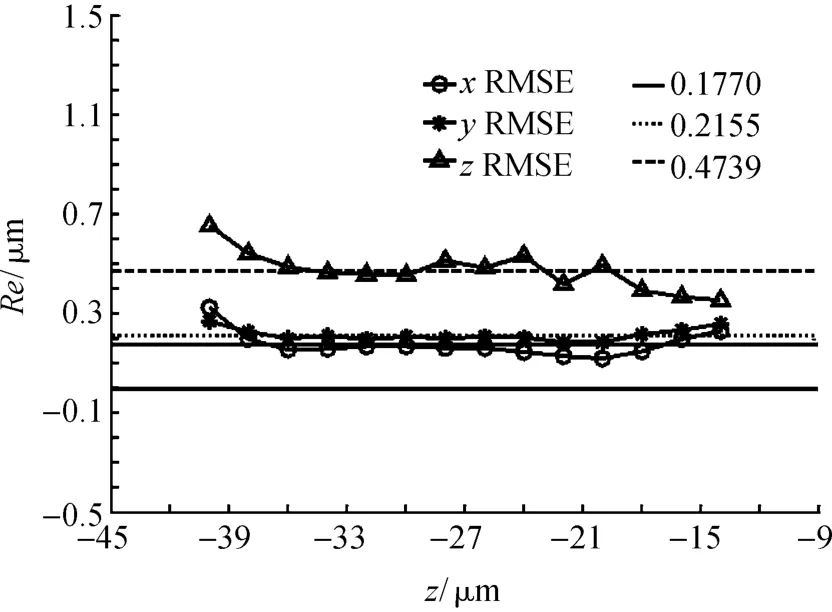
图10 粒子测量位置x／y／z误差分析Figure 10 Error analysis of particle's x／y／z positions measurement

3.3 倒置台阶绕流测量结果与分析

采用高速CMOS相机，以1000帧／s的扫描速率对倒置台阶结构微通道中粒子轨迹和流场进行了测量.对高速相机采集的图像序列经过维纳滤波去噪，获得高质量的散焦粒子图像；将同参考模式的相似度值大于0.99的三角形作为粒子对应的模式（图5）进行粒子识别；利用像点追踪软件Vide Spot Tracker v07.02对其相应的三个像点进行单独追踪（针对低体积密度溶液中粒子的追踪），计算三个像点构成的等边三角形质心，获得追踪粒子的质心；利用深度标定函数和x／y补偿函数对粒子的实际深度和水平位置进行计算和修正，获得了台阶绕流流场中荧光粒子的瞬时位置，最终实现粒子运动轨迹的追踪和速度矢量的测量.

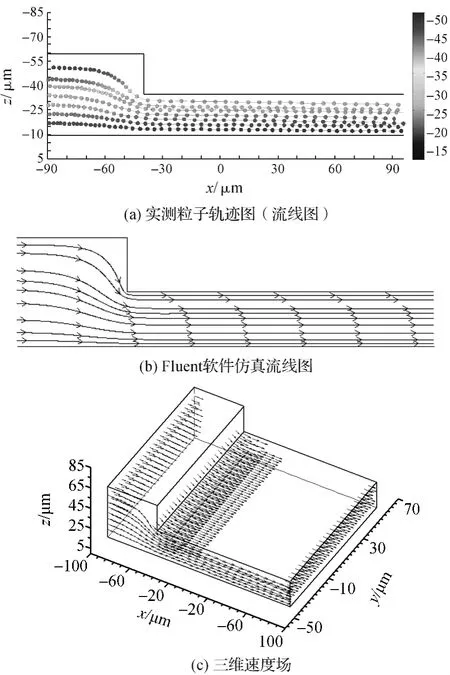
图11 倒置台阶微通道内粒子追踪轨迹及平均速度矢量场Figure 11 Particle trajectory and the average velocity vector field in a micro channel with inverted step

图11给出了流向尺度约为180μm范围内的粒子轨迹及流线和三维速度分布.其中图11（a）给出了流向和深度方向不同位置粒子运动的轨迹图.由于流动为定常，粒子运动的迹线也即为流场的流线.为了验证实测结果的有效性，图11（b）给出了采用流体动力学软件Fluent进行数值仿真结果，可以看到实测和仿真所获流型是一致的.对粒子轨迹坐标进行求导后可获得二维速度分布，在此基础上进行展向拉伸得到三维速度场分布（为了清楚起见，主要给出流场绕台阶拐点位置的三维分布），见图11（c）.该测量结果表明，粒子分层的运动轨迹符合后台阶绕流流场的基本特征，表明利用散焦粒子追踪测速技术能够实现三维流场的测量.

4 结 语

本文在通过对显微散焦粒子三孔挡板进行设计的基础上，搭建了高速显微散焦粒子测速系统.研究了散焦粒子图像与粒子三维空间之间的标定函数关系，编写了标定和粒子识别算法.针对倒置台阶结构微通道流动的粒子进行了三维追踪测速，获得了粒子的运动轨迹和微通道流动的速度矢量，实验结果验证了散焦测速系统的可行性和追踪测速算法的有效性.

［1］WILLERT C，GHARIB M.Three－dimensional particle imaging with a single camera［J］.Experiments in Fluids，1992，12：353－358.

［2］PEREIRA F，GHARIB M.Defocusing digital particle image velocimetry and three－dimensional characterization of two phase flows［J］.Measurement Science and Technology，2002，13：683－694.

［3］KAJITANI L，DABIRI D.A full three－dimensional characterization of defocusing digital particle image velocimetry［J］.Measurement Science and Technology，2005，16：790－804.

［4］KAJITANI L，DABIRI D.A full three－dimensional characterization of defocusing digital particle image velocimetry［J］.Measurement Science and Technology，2008，19：1－2.

［5］WU M，ROBERTS J W，BUCKLEY M.Three－dimensional fluorescent particle tracking at microscale using a single camera［J］.Experiments in Fluids，2005，38：461－465.

［6］YOON S Y，KIM K C.3Dparticle and 3Dvelocity field measurement in a micro volume via the defocusing concept［J］.Measurement Science and Technology，2006，17：2897－2905.

［7］PEREIRA F，LU J，CASTANO G E，et al.Microscale 3D flow mapping withμDDPIV［J］.Experiments in Fluids，2007，42：589－599.

［8］LU J，PEREIRA F，FRASER S E，et al.Three－dimensional real－time imaging of cardiac cell motions in living embryos［J］.Journal of Biomedical Optics，2008，13（1）：1－8.

［9］YOON S Y，YANG S.Microfluidic device for refractive index measurement of fluid sample［J］.Procedia Engineering，2010，5：1340－1343.

［10］YOON S Y，KHIM K D，KIM K C.Correlation of fluid refractive index with calibration coefficient for micro－defocusing digital particle image velocimetry［J］.Measurement Science and Technology，2011，22：1－5.

［11］TIEN W H，KARTES P，YAMASAKI T，et al.A color coded back lighted defocusing digital particle image velocimetry system［J］.Experiments in Fluids，2008，44：1015－1026.

［12］LIN D，ANGARITA－JAIMES N C，CHEN S Y，et al.Three dimensional particle imaging by defocusing method with an annular aperture［J］.Optics Letters，2008，33（9）：905－907.