磁流变技术的工程应用

李卫华

（伍伦贡大学，澳大利亚 伍伦贡 2522）

1 磁流变材料

1.1 磁流变液

磁流变液（MRF）是微米级的可极化粒子与载体溶液的混合物.其特点是：

1）在没有磁场作用下呈现牛顿流体状态；

2）在磁场作用下可以产生高强度屈服应力，如图1；

3）为电力控制和机械设备提供无噪声、反应迅速的控制.

1.2 磁流变弹性体

磁流变弹性体（MRE）是一种新型智能材料，如图2，它的组成颗粒有铁粒子和铁合金粒子，以硅胶、自然橡胶、高分子聚合物为载体.磁流变弹性体是一种典型的刚度可控的弹性材料，其剪切应力与应变的关系如图3.

图1 磁流变液的状态Figure 1 State of magnetorheological fluid

图2 磁流变弹性体Figure 2 Magnetorheological elastomers

图3 应力应变曲线图Figure 3 Relationship between shear stress and strain

2 磁流变技术在高铁上的应用

高速铁路具备很多优势：1）高效和安全；2）环保；3）单位运输成本低.但高铁仍然面对着问题，即振动问题和稳定性问题.普通车辆存在竖直方向的振动，火车存在横向振动，而临界速度是衡量高铁行驶稳定性的重要指标.

高速铁路在行驶过程中，高速引起的振动和噪音会导致：

1）乘坐不适和车身不稳定；

2）对周围环境造成噪音污染；

3）提高铁轨和轮对的维护成本.

针对以上问题，已经存在一些解决方案，如精心设计的被动阻尼系统通常用于高铁减振.但该方法仍有不足之处，即当高铁达到它的临界速度时，被动阻尼器往往会失去减振效能.所以研究高铁不稳定性机理并找到解决问题的方法是当前至关重要的.所以，接下来我们探究由振动引起的高铁的不稳定问题以及如何将磁流变技术应用于高铁以解决振动问题和不稳定性问题.

2.1 对振动引起的不稳定性问题的分析

2.1.1 数学模型

高速铁路行驶的数学模型如图4，该数学模型包括前转向架模型和后转向架模型，每个转向架架框包括一个一系悬架和一个二系悬架，含有四对轮对（两对在车身前部，另两对在车身尾部）.数学模型中有15个自由度，分别是：

图4 高铁行驶的模型Figure 4 Model of high speed rail

1）车身：横向运动，横摆运动和侧倾运动（3个自由度）；

2）转向架：前转向架和后转向架的横向运动和横摆运动（4个自由度）；

3）轮对：四个轮子的横向运动和横摆运动（8个自由度）.

高铁数学模型的数学表达式如下：

式（1）中，q＝［ycθcψcyω1ψω1yω2ψω2yω3ψω3yω4ψw4yt1ψt1yt2ψt2］.

式（1）的特征值如下：

式（2）中，n表示自由度个数，αj、βj分别表示系统动态矩阵第j个特征值的实部和虚部.

阻尼比的表达式为

当阻尼比值为零时，高铁即时速度为临界速度.

2.1.2 高铁速度对阻尼比的影响

图5表示火车速度对十五个自由度的阻尼比的影响.阻尼比越小，所对应的自由度越不稳定.从图5可以看出，由于后转向架轮对，后转向架框架的阻尼比非常小，甚至小于零，因此相比于其它自由度，后转向架轮对的四个自由度以及后转向架框架的两个自由度更不稳定.

2.1.3 悬架参数对临界速度的影响

如图6（a），当一系横向阻尼变化时，高铁临界速度主要受后转向架的后轮对的横向运动影响.如图6（b），当一系横向刚度变化时，高铁临界速度主要受后转向架后轮对和后转向架框架的横向运动影响.如图6（c），当二系横向阻尼不大于5×104N·s·m－1时，高铁的临界速度受到后转向架框架的横向运动和横摆运动的影响；当二系横向阻尼超过5×104N·s·m－1之后，后转向架后轮对的横摆运动和前转向架框架的横摆运动成为影响高铁临界速度的主要因素.如图6（d），后转向架框架的横向运动和横摆运动限制了高铁的临界速度.

从图6可以得出结论：高铁临界速度分别受后转向架框架的临界速度和后转向架轮对临界速度的影响.

图5 车速与阻尼比的关系曲线图Figure 5 Relationship between speed and damping ratio

图6 悬架参数与临界速度的关系图Figure 6 Relationship between suspension parameters and critical speed

从图7中可以得出，二系横向阻尼对提高临界速度起着至关重要的作用.然而，传统的被动二系横向阻尼器将被半主动磁流变阻尼器所取代，如图8.

图7 临界速度与阻尼的关系图Figure 7 Relationship between critical speed and damping

图8 二系横向阻尼器Figure 8 Secondary lateral damping

2.2 基于磁流变液阻尼器的半主动悬架系统

基于磁流变液阻尼器的半主动悬架系统结构如图9.

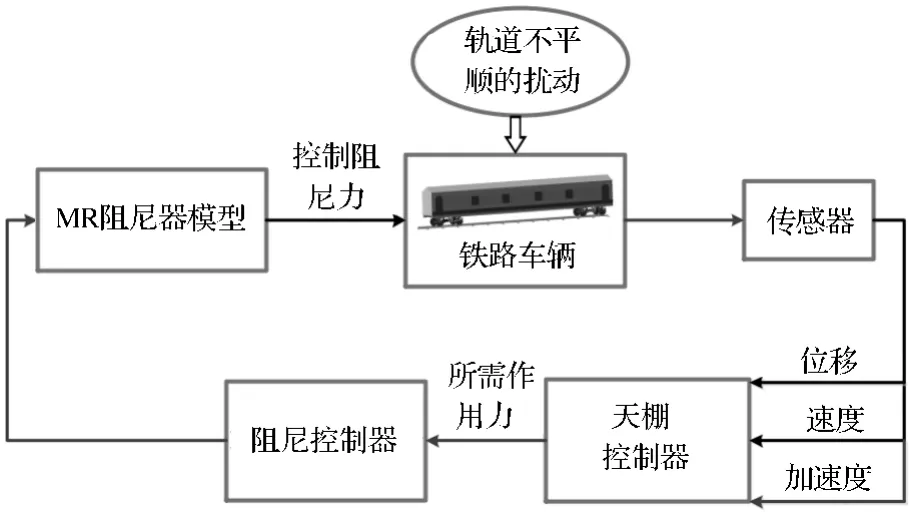
图9 基于磁流变液阻尼器的半主动悬架系统结构图Figure 9 Semi active suspension system structure diagram based on MR damper

图10（a）、（b）分别为搭载被动阻尼器和磁流变液阻尼器高铁对振动的响应曲线.从图10可以看到，在磁流变液阻尼器替代被动阻尼器后，高铁临界速度从275km／h增长到330km／h.

图10 不同阻尼器下高铁对振动的响应Figure 10 Response of high speed rail to vibration with different dampers

2.3 变刚度变阻尼悬架在高铁上的应用

变刚度变阻尼悬架系统不论是从理论角度还是实验角度都已经被验证比只变阻尼悬架系统能更有效的减振，如图11.但现有的变刚度变阻尼器件因为其本身的局限性不能应用于高铁.因此目前没有实际可用于高铁的变刚度变阻尼装置.所以目前需要解决以下问题：

图11 变刚度阻尼悬架Figure 11 Variable stiffness damping suspension

1）探究变刚度变阻尼悬架是否可以有效的应用于高铁；

2）如果有效，开发应用于高铁的变刚度变阻尼装置.

2.3.1 实验仿真

控制系统原理图如图12.

四种悬架系统的振动情况如图13和图14，从四种悬架系统的比较结果可以看出，变刚度变阻尼悬架能够最有效的减小高铁振动.因此目前面对的最大挑战就是设计开发实际可用于高铁的变刚度变阻尼装置.

图15分别展示了两种不同的变刚度变阻尼装置的结构设计.

图12 控制系统Figure 12 Control system

图13 四种悬架系统的加速度比较Figure 13 Acceleration comparison of four suspension systems

图14 四种悬架系统的加速度均方根比较Figure 14 Acceleration RMS comparison of four suspension systems

图15 两种结构设计图Figure 15 Structure of two designs

2.3.1.1 结构1的设计

变刚度变阻尼减震器的结构1的工作原理如图16，实物如图17，测试装备如图18.

图16 结构1的工作原理图Figure 16 Working principle of structure 1

图17 变刚度变阻尼减振器Figure 17 Variable stiffness variable damping shock absorber

图18 结构1的测试装备Figure 18 Experiment setup of structure 1

变刚度性能测试结果如图19，当电流从0A增加到1A时，有效刚度从8.7kN／m增加到24.5kN／m.

变阻尼性能测试结果如图20，当电流从0A增加到2A时，有效阻尼从16.2kN／（m·s－1）增加到29.7kN／（m·s－1）.

图19 变刚度性能测试结果Figure 19 Test results of variable stiffness performance

图20 变阻尼性能测试结果Figure 20 Test results of variable damping performance

对结构1进行数学建模，模型如图21.

图21 结构1的数学模型图Figure 21 Mathematical model of structure 1

其中，x2满足以下关系式：

参数（f1，f2，C1，和C2）和电流之间的函数关系如下：

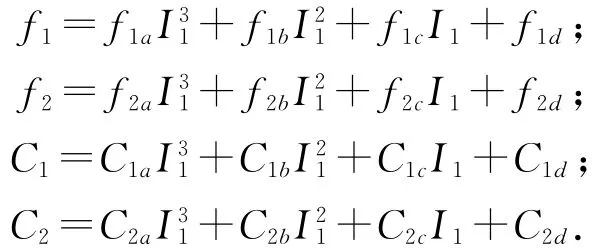
2.3.1.2 结构2的设计

变刚度变阻尼减震器的结构2的实物如图22，测试装置如图23.

图22 变刚度变阻尼减振器Figure 22 Variable stiffness variable damping shock absorber

图23 结构2的测试装备Figure 23 Experiment setup of structure 2

变刚度性能测试结果如图24，变阻尼性能测试结果如图25.

图24 变刚度性能测试结果Figure 24 Test results of variable stiffness performance

图25 变阻尼性能测试结果Figure 25 Test results of variable damping performance

2.3.2 结论

1）从仿真结果和理论分析可以看出二系横向悬架参数和一系纵向刚度是影响临界速度的主要因素.

2）相比于传统的被动二系横向阻尼器，磁流变液阻尼器能更好地提高高铁稳定性.

3）设计并加工了两种新型变刚度变阻尼减振器.仿真结果表明这两种减振器能够有效提高高铁乘坐舒适度.

3 建筑物智能隔震系统

基础隔震的概念在过去的50年中已经成为现实.更多新型的隔震概念和机制也纷纷兴起.

基础隔震的基本概念是将上部建筑和下部结构分离，是目前最普遍最有效的保护建筑物和桥梁的防震技术，被广泛应用于地震多发国家的土木结构的保护.目前基础隔震主要面临两方面的问题，一是地震的不可预测性和复杂多样的特点，二是传统的被动隔振器不能根据地震特点实现实时自我调节.所以我们研究的目标是将磁流变弹性体应用于隔震系统，开发具有高可调性的智能隔震器.

磁流变弹性体隔震器具有横向刚度可被外部磁场实时可控和节能两方面的优点.其工作原理是使被保护建筑物的自然频率尽可能的远离激振频率.以图26中的系统为例，整个系统的自然频率为

其中，keff＝f1（I），即磁流变弹性体的有效刚度是电流的函数，因此系统自然频率也是电流的函数，即f0＝f（I）.

图26 磁流变弹性体隔震系统Figure 26 Magnetorheological elastomer isolation system

3.1 多层磁流变弹性体隔震器

单层磁流变弹性体隔震器的例子［1］如图27，它存在三方面的局限性：1）竖直支撑能力有限；2）有效刚度变化范围小；3）横向剪切位移小，横向灵活性受限制.

图27 单层磁流变弹性体隔震器Figure 27 Single layer magnetorheological elastomer isolator

针对单层磁流变弹性体隔震器的局限性，设计了多层磁流变弹性体隔震器，其结构设计［2］如图28.它采用多层橡胶支座（LRB）的经典结构，用磁流变弹性体替代传统橡胶，利用电磁线圈产生磁场.多层磁流变弹性体隔震器具备以下优点：

图28 多层磁流变弹性体隔震器Figure 28 Multi layer magnetorheological elastomer isolator

1）经典的多层结构具有很强的竖直方向承载能力以及很大的竖直方向的刚度，同时，这种多层结构还具有比较软的横向刚度；

2）磁流变弹性体的机械性能在磁场作用下变化迅速，并使得隔震器具有很好的横向灵活性；

3）横向刚度变化范围大.

对多层磁流变弹性体隔震器进行实验测试，实验装置如图29.

图29 实验装置示意图Figure 29 Experimental apparatus

对多层磁流变弹性体隔震器的性能测试分为振幅依赖性、频率依赖性和磁场依赖性三方面，测试结果分别为图30、图31和图32.

1）振幅依赖性：在激振频率和应用电流值不变的情况下，磁滞回线的斜率（有效刚度）随着激振振幅的增大而减小.

2）频率依赖性：磁滞回线的闭合面积（等效阻尼）随着激振频率的增加而增加.

3）磁场依赖性：实验结果表明这种新型磁流变弹性体隔震器横向刚度最大变化率可达1730%，输出力最大变化率可达1579%.

图30 振幅依赖性测试结果Figure 30 Amplitude dependence test results

图31 频率振幅依赖性测试结果Figure 31 Frequency dependence test results

图32 磁场依赖性测试结果Figure 32 Magnetic field dependence test results

对多层磁流变弹性体隔震器进行数学建模，模型如图33，表达式为：

其中：k0—弹簧刚度；c0—系统阻尼系数；α∈（0，1）—磁滞回线的线性程度；

A，n，β以及γ属于无量纲参数，主要控制磁滞回线的形状.

在提出的唯象模型中，一共有六个参数需要辨识.选择的辨识方法是MATLAB－Simulink中的最小二乘法结合信赖域反射算法，其优化目标是最小化输出力的均方根

其中：N—输入输出对的个数，Fp—模型预测的输出力，Fe—实验测得的输出力.模型参数辨识结果如表1，拟合效果如图34.

图33 数学模型Figure 33 Mathematical model

表1 模型参数辨识结果Table 1 Model parameter identification results

图34 拟合效果图Figure 34 Fitting effect

图35表示输出力的追踪图，以及模型预测力和实验所得力之间的误差随时间的变化曲线.可以看出误差浮动在可接受的变化范围内.

图36给出多组拟合结果，进一步验证所提唯象模型描述多层磁流变弹性体隔震器的能力［3］.

图35 输出力追踪图Figure 35 Output force tracing

图36 多组拟合结果Figure 36 Different fitting results

磁流变弹性体隔震器仍面临巨大挑战，即使在通常状态下磁流变弹性体隔震器必须要一直通电才能提供足够大的刚度来保持建筑物的稳定性，这种要求将会造成巨大的能量浪费.因此一种具有“负刚度”特性的磁流变弹性体隔震器亟需开发.这种隔震器在通常状态下可以提供足够大的刚度而不需要能量消耗，并且当地震发生时能提供比较软的刚度以达到分离上层建筑和下部结构的目的.

3.2 具有“负刚度”特性的磁流变弹性体隔震器

3.2.1 结构设计

具有“负刚度”特性的磁流变弹性体隔震器设计亮点是永磁铁和电磁线圈的混合系统，如图37.该结构的理论基础是磁场可叠加性和电磁场的方向和大小是可控的.

图37 结构设计图Figure 37 Structure design

具有“负刚度”特性的磁流变弹性体隔震器的工作原理如图38.（a）中电磁线圈产生的电磁场的方向与永磁场的方向相同，电流越大，两个磁场的叠加总和越大，此时，隔震器的刚度随电流的增大而增大.（b）中电磁线圈产生的电磁场的方向与永磁场的方向相反.在一定范围内，电流越大，两个磁场的叠加总和越小.此时，隔震器的刚度随电流的增大而变小.隔振器样机如图39.

3.2.2 性能测试

对隔震器进行性能测试，分别是振幅依赖性、电磁场依赖性、传递率以及有效刚度与所加电流的关系，测试结果分别为图40、图41、图42和图43.

图38 工作原理图Figure 38 Working principle

图39 样机Figure 39 Prototype

1）振幅依赖性：随着激励振幅的增大，磁滞回线的非线性趋于明显.这是由于橡胶基质之间的弹性抵抗力以及铁粒子之间的电磁吸引力阻止了磁流变弹性体的链结构的扩展和延伸.

2）电磁场依赖性：当电流为最大值4A时，有效刚度为最小值.最大刚度与最小刚度之间的变化率达182.4%.

3）传递率：从图42中可以看出，自然频率随着电流的增大而减小.自然频率的最大值和最小值之间的变化率达135%.

4）有效刚度与所加电流的关系.

图40 振幅依赖性测试结果Figure 40 Amplitude dependence test results

图41 电磁场依赖性测试结果Figure 41 Electromagnetic field dependence test results

图42 传递性测试结果Figure 42 Transmissibility test results

3.2.3 实验验证

三层楼建筑物模型如图44，该模型系统的动态方程如式（7）.

图44 三层建筑物模型Figure 44 Scaled three story building with MRE isolators

模糊控制的推理规则如表2.

表2 模糊控制的推理规则Table 2 Fuzzy inference rules

被动与半主动磁流变弹性体隔震器之间的比较如图45，在模糊控制作用下，层间位移和每层楼的对地加速度都明显的变小.

图45 被动与半主动磁流变弹性体隔震器的比较Figure 45 Comparison between passive and semi active MRF isolator

图46表示的是整个实验部分的实验装置.测量地震信号从地面到第一层楼的传递率所用的激振信号是正弦扫频信号.图47中分别展示了半主动和被动控制条件下的传递率.可以观察到，半主动作用下的传递率（绿色的曲线）明显比被动作用下的传递率低.

图46 实验装置Figure 46 Photograph of the practical experimental setup

图48表示的是在固定基座，被动和半主动三种控制状态下的三楼与一楼的相对位移.可以明显的看出，在固定基座的情况下，相对位移最大，说明楼体晃动最大；而在半主动控制下，相对位移

图47 半主动和被动控制条件下的传递率Figure 47 Transmissibility of earthquake motion to the building for passive and semi－active cases

在整个时间段内保持最小.

图48 三种控制状态下的相对位移Figure 48 Relative displacement for the three control conditions

图49分别表示三楼与二楼在三种控制条件下的对地加速度响应.可以明显的看出，在固定基座的情况下，三楼与二楼的加速度幅值在整个时间段内最大，而半主动控制下的加速度始终保持最小.

图49 对地加速度响应Figure 49 Acceleration response of floor

3.3 结论

1）经实验验证，提出的新型磁流变弹性体隔震器能够实现“负刚度”变化，即：能够在通常状态下提供大刚度保持上层建筑的稳定；在地震发生时，又能提供小刚度使上层建筑和下部结构分离，起到保护上层建筑的目的.同时，这种新型隔震器在通常状态下不需要能源消耗，达到了节能的目的.

2）这种新型磁流变弹性体隔震器不仅能实现“负刚度”，当反方向电流信号应用于此隔震器时，其横向刚度也会在一定程度内随着电流的增大而增大.

3）经仿真和实验验证，此磁流变弹性体隔震器能够有效的减小振动，保护建筑物.

4 基于磁流变弹性体的调谐质量阻尼器在建筑物上的应用

4.1 优点

基于隔震器的多层结构，我们开发了一种新型的多层结构的基于磁流变弹性体的调谐质量阻尼器，如图50.它的优点是：

1）其刚度可控性使得此调谐质量阻尼器能够适应不同的风载和地震；

2）比传统的调谐质量阻尼器更有效，其中振子和电磁线圈都可以充当减振的有效质量；

3）振子更具灵活性，具有更大的振动振幅.

图50 调谐质量阻尼器结构Figure 50 Tuned mass damper structure

4.2 性能测试

对调谐质量阻尼器结构进行测试，测试装置如图51，测试结果如图52，此调谐质量阻尼器的自然频率可以从3.1Hz变化到7.1Hz.

图51 性能测试装置Figure 51 Experimental set up for property test

图52 传递率Figure 52 Transmissibility

4.3 建模

系统数学模型如图53，表达式如式（8）.

模糊控制器的控制逻辑如表3.

表3 模糊控制器的控制逻辑Table 3 Fuzzy logic controller

图53 建筑物数学模型Figure 53 Mathematical model of the scaled building

4.4 仿真结果

1）激振信号为扫频信号：如图54，在特定电流（0A，0.5A，1A，1.5A等）作用下的阻尼器都被定义为被动阻尼器.从图中可以看出，每个电流状态下的传递率都有一个最低点，这个最低点即此状态下调谐质量阻尼器的最佳吸振点.可以看出最佳吸振点在自然频率附近，当激振频率远离任何一个状态下的自然频率时，传递率就会明显上升.而由半主动控制下的传递率可以看出，此条传递率曲线一直保持最小，不会随着激振频率的变化有突然的上升.这个结果充分说明了半主动调谐质量阻尼器能够很好的追踪激振频率，降低地面到楼层的传递率.

2）激振信号为模拟地震信号：如图55，在特定电流（0A，0.5A，1A，1.5A等）作用下的阻尼器都被定义为被动阻尼器.两图分别表示了每个楼层的加速度以及对地位移.可以从图中明显的看出，无论是加速度还是相对位移，半主动控制下的响应都保持最小值.

4.5 实验验证

实验装置图如图56.

图54 传递率Figure 54 Transmissibility

图55 第三层楼相对地面的峰值Figure 55 Peak values of three floors with respect to the ground

图56 实验装置图Figure 56 Photograph of the practical experimental setup

实验结果如下：

1）激振信号为扫频信号：对应于前面的仿真结果，如图57，在特定电流（0A，0.5A，1A，1.5 A等）作用下的阻尼器都被定义为被动阻尼器.从图中可以看出，半主动控制下的阻尼器可以将各个电流状态下的传递率的最低点（即吸振点）连接起来，得到一条最优传递率.这充分说明半主动调谐质量阻尼器能够很好的追踪激振频率，降低地面到楼层的传递率.

2）激振信号为模拟地震信号：图58（a）、（b）分别为三楼与地面间的相对位移以及二楼与地面间的相对位移.可以看出，无论是三楼还是二楼，在没有调谐质量阻尼器时，其相对位移的峰值最大；在被动调谐质量阻尼器（此处没有电流作用时被定义为被动调谐质量阻尼器）作用下，相对位移峰值比没有调谐质量阻尼器时的小，而在半主动控制作用下，其相对位移是最小的，说明在模糊控制作用下，提出的磁流变弹性体调谐质量阻尼器能够有效的减小楼层与地面间的相对位移.

3）激振信号为模拟地震信号：从图59可以看出，在某些时段，没有调谐质量阻尼器情况下的加速度响应与应用了被动调谐质量阻尼器情况下的响应不相上下.然而，半主动控制下的加速度始终是最小的.

图57 实验获取的传递率Figure 57 Experimentally obtained transmissibility

图58 地面和楼层间的相对位移Figure 58 Relative displacement between ground and floor

图59 楼层的加速度Figure 59 Acceleration of floor

4）激振信号为模拟地震信号：图60为在八种控制条件下，每层楼的加速度信号和层间相对位移峰值.可以看出，半主动控制下的加速度信号和相对位移信号峰值最小.

图60 不同控制条件下的建筑物楼层峰值Figure 60 Peak of the building floors with different TMDs

4.6 结 论

1）此基于磁流变弹性体的调谐质量阻尼器在不同的电流信号作用下能够实现移频.

2）经仿真和实验验证：相比于传统的调谐质量阻尼器，这种新型设计能够更有效的保护建筑物，降低地震对建筑物的伤害.

［1］BEHROOZ M，WANG Xiaojie，GORDANINEJAD F.Performance of a new magnetorheological elastomer isolation system［J］.Smart Materials and Structures，2014，23（4）：045014.

［2］LI Yancheng，LI Jianchun，TIAN Tongfei，et al.A highly adjustable magnetorheological elastomer base isolator for applications of real－time adaptive control［J］.Smart Materials and Structures，2013，22（9）：095020.

［3］YANG Jian，DU Haiping，LI Weihua，et al.Experimental study and modeling of a novel magnetorheological elastomer isolator［J］.Smart Materials and Structures，2013，22（11）：117001.