面板数据的灰色矩阵相似关联模型及其应用

崔立志，刘思峰

(1.安徽工业大学商学院，安徽 马鞍山 243032；2.南京航空航天大学经济与管理学院，江苏 南京 211106)

面板数据的灰色矩阵相似关联模型及其应用

崔立志1，刘思峰2

(1.安徽工业大学商学院，安徽 马鞍山 243032；2.南京航空航天大学经济与管理学院，江苏 南京 211106)

根据灰色关联分析的基本思想，在定义了面板数据矩阵表现形式的基础上，以指标为研究对象，从个体和时间两个维度分别衡量了相关因素矩阵与系统特征行为矩阵之间的发展速度指数和增长速度指数的接近程度，并以此作为关联度的度量，将灰色关联分析由传统的向量空间拓展到矩阵空间，提出了面板数据的灰色矩阵相似关联模型，并讨论了其性质。最后以CO2排放为例，通过测算中部六省2005—2012年碳排放量，建立了中部地区碳排放影响因素的灰色矩阵相似关联模型，实例表明，该模型简单，且具有良好的应用性。

灰色矩阵相似关联度； 发展速度指数；增长速度指数；碳排放

1 引言

灰色关联分析是灰色系统理论的重要组成部分，也是灰色系统分析、灰色决策、灰色聚类的基石。它是研究系统内部因素之间关联程度的一种数学模型，其基本思想是根据数据序列曲线的几何形状判断不同序列之间的联系是否紧密[1]。自从邓聚龙教授提出灰色关联分析模型以来，众多学者相继加入到灰色关联研究中来，把研究范围从早期的点关联系数模型扩展到全局视角的灰色关联分析模型，取得了不少有价值的研究成果，如灰色绝对(相对)关联度模型[2-3]、B型关联度模型[4]、C型关联度模型[5]、T型关联度模型[6]、灰熵关联度模型[7]、灰色欧几里德关联度[8]、斜率关联度模型[9]以及比较分析几种关联度模型具有的性质[10-13]和应用[14-15]。这些学者从不同的方面对关联度进行了认真的研究，都取得了一定的应用效果，但是以上研究主要适用于截面数据与时间序列数据的关联分析。由于现实中存在的大量实际问题和科学难题需要运用矩阵数据、面板数据等分析方法去研究解决，因此研究高维场数据的关联分析问题是一个有价值的研究方向[16]。从现有研究来看，主要研究思路有：第一，把已有关联模型与其他方法，如AHP，SVM等结合，从而拓宽灰色关联模型的应用范围[17-18]；第二，直接把曲线之间关系拓展到曲面之间关系，通过探讨面板数据几何特征的三角曲面簇表示方法，分析了三维空间中面板数据的各指标几何相似性，从而建立三维灰色绝对关联模型[19]，这种扩展的灰色关联分析主要受到指标行为矩阵序列对应的曲面簇的表示方式的影响，也就是说曲面簇表示方式不同会影响到关联度；第三，为了体现多指标面板数据的时空特征，综合考虑个体的指标动态发展水平和变异程度，利用“水平”距离、“增量”距离和“变异”距离对面板数据时空演变的相似性进行测度，建立灰色矩阵关联分析模型[20]，尽管该关联度全面考虑了面板数据的绝对量指标、增量指标和时序波动性，但是存在集结困难问题；第四，借鉴凹凸性的数学描述，利用黑塞矩阵的半正定性在三维空间中定义凸度，以相关因素序列之间的相对凹凸度的接近性作为关联度的度量，建立了灰色凸关联分析模型[21]，显然以相对凸度定义的关联度存在从连续形式向离散形式跳跃而产生的偏差。总之，上述研究拓展了灰色关联分析的适用范围，同时也丰富了面板数据的灰色关联模型。

面板数据广泛地存在经济与管理问题研究中，是现实生活中常见的数据形式之一。它是截面数据和时间序列的组合，具有截面维度和时间维度的特征。因此，面板数据表征的对象间相似性的度量可以从截面维度和时间维度综合考虑，充分挖掘多指标面板数据蕴涵的两个维度的信息。本文受灰色关联分析的主要研究成果及基本思想的启发，充分利用面板数据两个维度的信息，从分析事物发展规律的角度出发，基于参考序列和比较序列的相对差异程度建立了面板数据的灰色关联模型，最后利用该关联模型对中部地区六省的CO2排放影响因素进行分析。

2 面板数据的灰色关联分析模型

2.1 面板数据的矩阵序列

面板数据是由多个个体(对象)在多个指标的不同时点上的指标值构成的集合，反映了所有个体在相应指标下的发展水平及其发展动态。从横截面来看，同一时点的指标值反映了不同个体的截面发展水平；从纵剖面看，是每个指标的动态发展水平；从几何角度看，可以把每个个体的各个指标在不同时点上的观测值与三维空间中的点一一对应。因此，对于面板数据中的每个研究对象，能够得到如下的矩阵。

定义1 设有M个对象，每个研究对象有N指标，观测期数为T。面板数据中第i个对象第m个指标在t时期(时点)的指标值记为xi(m,t)>0，其中i=1,2,…,N，m=1,2,…,M，t=1,2,…,T，则称：

(1)

为指标m的数据矩阵，那么所有的指标对应的数据矩阵X=(X1,X2,…,XN)称为面板数据的矩阵序列。若在每个时期每个指标上的对象都一样，则为平衡面板数据的矩阵序列；反之，则称为非平衡面板数据的矩阵序列。

本文主要研究平衡面板数据的矩阵序列，对于非平衡面板数据的矩阵序列，可以用预测方法(如GM(1,1)等)补齐所有缺失值，然后按照平衡面板数据的矩阵序列处理方式进行。

显然当M=1，即只有一个对象时，面板数据就退化为关于对象的时间序列；当T=1，即只有一期时，面板数据就退化为关于指标的截面数据。因此，面板数据的矩阵序列是对截面数据或时间序列在维数上的扩充。

定义2 若i为指标序号，则Xi(m)为对象m在指标i上的观测值，即：

Xi(m)=(xi(m,1),…,xi(m,T))T

(2)

Xi(m)称为对象m的行为指标序列,则面板数据的矩阵可以表述为Xi=(Xi(1),Xi(2),…,Xi(M))T，表示所有对象i在指标m上的观测值。

定义3 若t为时期序号，则Xi(t)为指标i在所有对象上的观测值，即：

Xi(t)=(xi(1,t),…,xi(M,t))T

(3)

Xi(t)称为指标m的行为时间序列。面板数据的矩阵可以表述为Xi=(Xi(1),Xi(2),…,Xi(T))，表示所有时期的指标观测值。

2.2 面板数据的截面维度和时间维度特征及表征

面板数据的矩阵序列中每个矩阵代表了相应的系统行为指标。矩阵的列描述每个对象在某一时期指标的截面特征，而矩阵的行反映对象的时间特征。在利用面板数据进行灰色关联分析时，要体现面板数据的截面和时间维度特征。为了能够准确刻画面板数据的维度特征，本文利用相异度(Dissimilarity)对对象之间的相似性进行反向度量，相异度越小，则相似性越大[22]。一方面，从截面维度考察不同对象间指标的发展速度差异，以相对发展速度指数来表征；另一方面，从时间维度衡量指标增长速度差异，以动态增长速度来表征，分别见定义4和定义5。

定义4 以发展水平指数来表示对象i和j之间发展水平差异：

(4)

其中Δij(m,t)=xi(m,t)-xj(m,t)。Δij(m,t)表示观测值在同一时期的发展水平差异，它是从截面维度考察了不同对象之间的发展水平差异。d1ij(m,t)表示i和j相对发展速度的差异程度。显然若指标随着时间都呈同向变化，即变异程度较小，则两者越相似；反之两者变化方向相反，则变异程度较大，两者的相似性也较差。

定义5 对象i和j之间的动态增长速度指数为：

(5)

其中Δi(m,t)=xi(m,t)-xi(m,t-1)，Δj(m,t)=xj(m,t)-xj(m,t-1)，t=2,3,…,T。Δi(m,t)和Δj(m,t)分别为表示指标两个相邻时期的增量，它衡量了指标的动态增长情况。d2ij(m,t)表示i和j的观测值增长的变异程度，显然若指标随着时间都呈同向变化，即变异程度较小，则两者越相似；反之两者变化方向相反，则变异程度较大，两者的相似性也较差。

在利用定义4和5时，首先必须对不同指标进行无量纲处理，常用的无量纲处理有初值化、均值化等，具体参考相关文献，本文采用初值化处理方式。d1ij(m,t)和d2ij(m,t)能够很好地表征相应指标发展水平及其变化趋势上的差异程度。

2.3 面板数据的灰色关联模型

定义6设正的系统行为矩阵序列Xi，i=1,2,…,N如定义1，并假设X0为正的系统特征行为矩阵，而X1,X2,…,XN为分别系统相关因素矩阵。则称:

(6)

(7)

为Xi和X0在点(m,t)的灰色矩阵相似关联系数，其中d1i0(m,t)和d2i0(m,t)类似定义4和5。则称:

(8)

(9)

分别为发展速度关联度和增长速度关联度。称综合关联度:

γi0=ω1γ1i0+ω2γ2i0

(10)

为灰色矩阵相似关联度，其中0≤ω1≤1 ，0≤ω2≤1，且ω1+ω2=1 。若有γi0≥γj0，则称相关因素Xi与X0的关联优于因素Xj与X0的关联，记Xi≻Xj，其中称“≻”为由灰色矩阵关联度导出的关联序。

定理1 面板数据的灰色矩阵关联度具有以下基本性质：(1)规范性，0<γi0≤1；(2)对称性；(3)接近性；(4)可比性；(5)唯一性。

灰色矩阵相似关联度模型不仅考虑了面板数据的发展水平差异和增长速度差异，而且构建了基于多指标面板数据相似性测度的计算模型。

3 实例分析

了解中部地区二氧化碳排放现状及其主要影响因素，既是实现低碳发展的内在需要，也有助于实行中部地区节能减排和改善环境质量。

从现有研究文献来看，识别碳排放的关键影响因素并对其效应进行准确的测度，既是采取碳减排行动的重要基础，也是气候变化领域研究的主要内容之一。因此，众多学者加入到碳排放影响因素研究中来，取得了丰硕的成果[23-26]。本文利用灰色矩阵关联模型对中部地区二氧化碳的主要影响因素进行分析，样本区间为2005—2012年，选取二氧化碳排放量、人口规模、人均GDP、能源强度和城市化水平等五个指标。

由于没有直接公布我国及其省域的CO2排放量，因此必须运用相关方法进行估算，估算方法参照IPCC(2006)以及国家发展改革委员会能源研究所的方法，对中部地区六省的2005—2012年CO2排放量进行测算。本文主要考虑人类活动导致的CO2排放，即人工排放。人工排放CO2主要来自化石能源消费和水泥生产过程。由于水泥主要是由石灰石高温煅烧而来，而石灰石的主要成分是CaCO3，CaCO3经过高温煅烧会释放大量CO2，即CaCO3→CaO+CO2↑。

化石能源燃烧产生的CO2排放的计算公式为：

(11)

水泥生产过程排放CO2的计算公式：

CC=Q×EF

(12)

其中CC表示水泥生产过程中由于发生的化学反应而产生的CO2排放量；Q表示水泥的产量，单位为万吨；EF表示水泥生产过程的CO2排放系数。

因此，本文测算中部六省的CO2排放量主要包括能源直接燃烧产生的CO2排放量和水泥行业生产过程中石灰石煅烧而产生的CO2排放量，不包含水泥生产过程中消耗的能源燃烧而产生的CO2排放量。

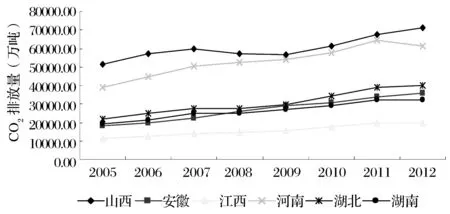
图1 中部六省CO2排放量

根据式(9)和(10)测算得到中部六省2005—2012年的CO2排放，见图1。中部地区的碳排放基本上处趋势，山西省碳排放居六省之首，2012年碳排放达到7.1亿吨；其次是河南、湖北、安徽和湖南紧随其后，江西省碳排放最少。

根据相关文献选取影响碳排放的一些重要因素包括：人口规模、人均GDP、城市化水平、能源强度。这些指标中人口规模，是个时点序列，以年末人口数来表示；人均GDP，通过价格指数换算，剔除通货膨胀因素，以2005年不变价格表示；城市化水平以城市人口占比表示；能源强度通常以单位GDP能耗表示，在本文的计算中GDP采用2005年不变价格。能源强度不仅是衡量能源效率提高的重要指标，而且直接影响着碳排放。从图2可以看出，山西能源强度最高，其能源强度在2吨标准煤/万元以上，江西能源强度最低，其能源强度从2005年的1.057吨标准煤/万元下降到2012年的0.769标准煤/万元；另外，中部六省能源强度都呈下降趋势，2012年能

源强度达到1吨标准煤/万元以下的有江西、安徽和河南。

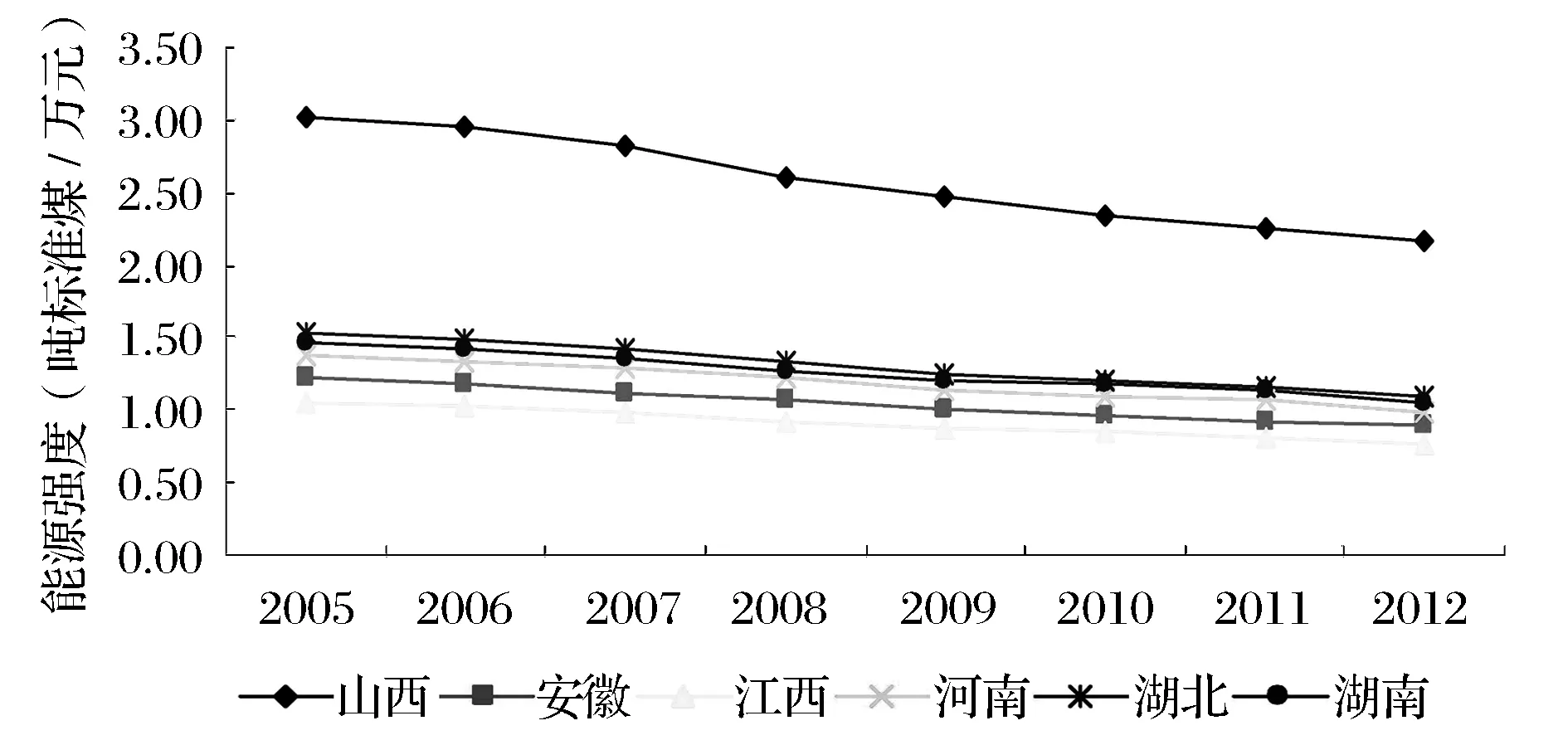
图2 中部六省以2005年不变价计算的能源强度

所有数据来源于相关的《中国统计年鉴》、《中国能源统计年鉴》以及各省的统计年鉴。

根据本文提出的灰色矩阵相似关联模型计算中部六省CO2排放量与人口规模、人均GDP、能源强度和城市化水平之间的关联度，见表1所示。

从表1可以看出，中部地区的各个省份的人口规模、人均GDP、城市化水平与CO2排放量的关联度比较高。

第一，从各个地区来看，山西省CO2排放量与人口规模、人均GDP、能源强度和城市化之间的关联度由高到低依次为：城市化水平≻人口规模≻人均GDP≻能源强度；安徽省关联序为：人均GDP≻城市化水平≻人口规模≻能源强度；江西省关联序为：人均GDP≻城市化水平≻人口规模≻能源强度；河南省关联序为：人均GDP≻城市化水平≻人口规模≻能源强度；湖北省关联序为：人均GDP≻城市化水平≻人口规模≻能源强度；湖南省关联序为：人均GDP≻城市化水平≻人口规模≻能源强度。从指标上来看，CO2排放量与人口规模关联度比较大，关联度都达到0.8以上，其中最大的关联度是山西省，达到0.918；CO2排放量与人均GDP关联度比较大，除了山西的关联度接近0.9以外，其他五省的关联度高于0.9；CO2排放量与能源强度关联度较小，关联度最小的是河南省，仅为0.565，CO2排放量与城市化水平关联度也比较大，达到0.85以上。

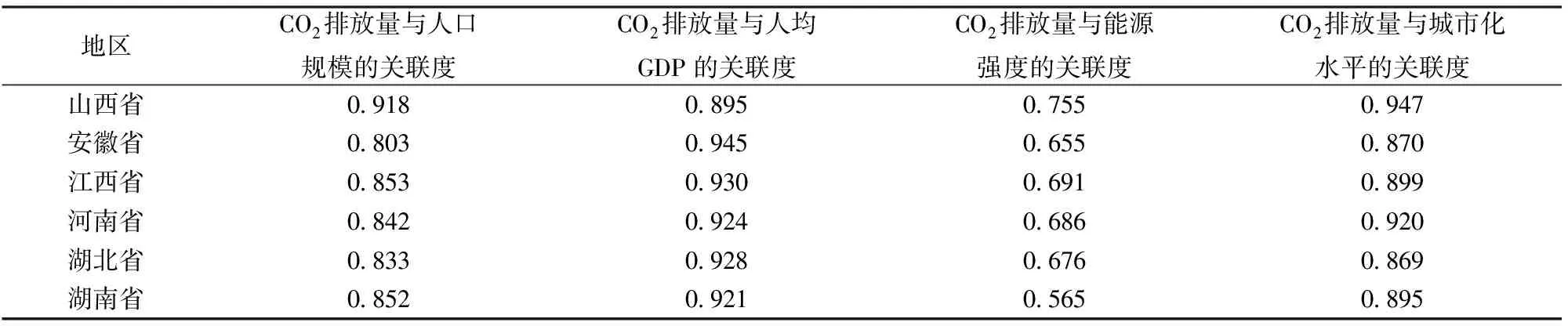
表1 中部地区各省CO2排放量与主要因素的关联度

第二，与大多数文献研究一致，人口对二氧化碳排放具有显著的影响。根据本文的研究，人口规模对碳排放的关联度在0.8以上。中部地区庞大的人口基数是二氧化碳排放量逐年增长的主要原因之一。中部六省中山西省的人口与碳排放关联度最大，主要是因为其年均人口增幅最大，为0.923%。较高的人口增长会对能源产生越来越多的需求，进而由能源消费产生的碳排放也比较多。

第三，中部地区经济快速增长，根据测算，以2005年不变价计算的样本期年均人均GDP增速分别为：山西9.839%，安徽11.974%，江西10.446%，河南10.627%，湖北11.564%，湖南10.849%，中部六省增速全部高于同期全国8.58%的增长率。因此，中部地区经济高速发展，必然伴随着对能源消费的巨大需求，进而二氧化碳排放总量也快速上升，主要表现为人均GDP和碳排放的关联度非常大，其中关联度最大的是安徽省，这与安徽省经济增长速度在中部地区排名第一息息相关。

第四，城市化水平也是影响中部地区碳排放的主要因素之一。随着经济的快速发展，中部地区的城市化水平也在不断提高。到2012年，山西和湖北城市化水平最高，都超过50%。城市化是经济社会发展中的重要内容，它会导致人们生产生活方式和土地利用类型发生变化，进而影响碳排放。一方面，人们在城镇化进程中会提高自身的消费水平和生活习惯，这会增加对能源的消费，推动碳排放的增长，另一方面，人口城镇化伴随耕地、林地等的占用，使得土地用途发生变化，导致这些土地从“碳汇”转变为“碳源”。

第五，能源强度反映了经济增长过程中能源利用效益，也即经济增长在多大程度上依赖于高能耗产业。从中部六省来看，山西省能源强度最大，超过2吨标准煤/万元，山西省能源强度和碳排放关联度最大，达到0.755，这与山西省的实际情况相符。山西省作为我国煤炭生产大省和能源基地，高能耗和高排放的煤炭产业山西省的支柱产业，在国民经济中占有重要地位。

4 结语

本文在灰色关联理论基本思想的启发下，充分利用面板数据的截面维度和时间维度，提出了用发展速度指数和增长速度指数来表征面板数据的时空特征，并在此基础上建立了灰色矩阵相似关联模型，该模型具有规范性、唯一性、对称性和相似性等性质。最后利用该模型对我国中部地区六省CO2排放的主要成因进行了分析，通过实例验证了该模型的有效性。研究结果表明：① 该灰色关联模型不仅计算简单，计算量小，在实际中具有良好的实用性，而且进一步拓宽了灰色关联度模型的应用领域，为多指标面板数据的相似性测度提供了一种新思路；② 根据实证分析结果，本文认为中部地区应从影响碳排放的主要因素入手，寻求节能减排得有效途径。首先，在碳减排的战略中，人口总量的控制依然是一个重要的方面，进一步减缓人口增长速度有利于减少碳排放；其次，在中部地区经济的快速发展中，可以通过优化产业结构，大力发展低碳产业、第三产业和服务业，积极推进资源节约型和环境友好行社会建设从而改变中部地区粗放增长特征；再次，在城市化进程中，需要考虑环境资源的约束，并且提高土地等资源的集约利用，走资源节约型的城市化发展道路；最后，中部地区需要加强普及提高能源利用效率的低碳技术，可以借鉴国内外先进经验和技术，逐渐改变以煤炭为主的能演消费结构，推广使用清洁能源，实行清洁生产，各省可以优先推广和发展符合本省实际情况的节能减排技术。

[1] 邓聚龙.灰理论基础 [M]. 武汉:华中科技大学出版社, 2002.

[2] Liu Sifeng, lin Yi. Grey information: Theroy and practical application [M].London:Springer-Verlag, 2006.

[3] 刘勇，刘思峰， Forrest J. 一种新的灰色绝对关联度模型及其应用[J]. 中国管理科学, 2012, 20(5):173-177.

[4] 王清印. 灰色B型关联分析[J].华中理工大学学报,1989,17(6): 77-82.

[5] 王清印,赵秀恒. C型关联分析[J]. 华中理工大学学报,1999,27(3): 75-77.

[6] 唐五湘. T型关联度及其计算方法[J].数理统计与管理,1995,14(1): 34-37.

[7] 张岐山,郭喜江.灰关联熵分析方法[J].系统工程理论与实践,1996,8(8):7-11.

[8] 赵艳林,韦树英,梅占馨.灰色欧几里德关联度[J].广西大学学报(自然科学版),1998,23(1): 10-13.

[9] 党耀国,刘思峰.灰色斜率关联度的改进[J].中国工程科学,2004,6(3): 23-26.

[10] 肖新平.关于灰色关联度量化模型的理论研究和评论[J].系统工程理论与实践,1997,17(8): 76-81.

[11] 吕峰,刘翔,刘泉.七种灰色系统关联度的比较研究[J].武汉工业大学学报,2000,22(2): 41-43.

[12] 谢乃明,刘思峰. 几类关联度的平行性和一致性[J]. 系统工程,2007,25(8): 98-103.

[13] 崔杰,党耀国,刘思峰.几类关联度的平行性和一致性[J].系统工程,2009,27(4): 65-70.

[14] 胡彦蓉，刘洪久，吴冲. 大学生运动服装品牌忠诚度影响因素的灰色关联度分析[J]. 中国管理科学, 2013,(专辑): 31-37.

[15] Lu I J, .Lin S J, Lewis C. Grey relation analysis of motor vehicular energy consumption in Taiwan [J]. Energy Policy, 2008,(36): 2556-2561.

[16] 刘思峰,蔡华, 杨英杰，等. 灰色关联分析模型研究进展[J].系统工程理论与实践,2013,33(8):2041-2046.

[17] Wang Jiangjiang, Jing Youyin, Zhang Chunfa， et al. Integrated evaluation of distributed triple-generation systems using improved grey incidence approach[J]. Energy, 2008, 33(9): 1427-1437.

[18] Jiang Hui, He Wenwu. Grey relational grade in local support vector regression for financial time series prediction[J]. Expert System with Application, 2012,39(3): 2256-2262.

[19] 张可,刘思峰.灰色关联聚类在面板数据中的扩展及应用[J].系统工程理论与实践,2010,30(7):1253-1259.

[20] 钱吴永,王育红,党耀国等. 基于多指标面板数据的灰色矩阵关联模型及其应用[J].系统工程,2013,31(10):70-74.

[21] 吴利丰,刘思峰.基于灰色凸关联度的面板数据聚类方法及应用[J].控制与决策,2013,28(7):1033-1045.

[22] 张贤达. 矩阵分析与应用[M]. 2版. 北京：清华大学出版社，2013.

[23] 张毅，夏炎. 工业化过程中碳排放消费建设比的演变规律研究[J]. 中国管理科学, 2012,20(2): 159-166.

[24] 吴振信，谢晓晶，王书平. 经济增长、产业结构对碳排放的影响分析——基于中国省际面板数据[J]. 中国管理科学, 2012, 2(3): 161-166.

[25] 赵泉午，杨茜. 考虑CO2排放量的城市专业物流中心选址研究[J]. 中国管理科学，2014，22(7)：124-130.

[26] Wang Yiming, Zhang Pei, Huang Dake, et al. Convergence behavior of carbon dioxide emissons in China[J]. Economic Modelling, 2014, 43: 75-80.

Grey Matrix Similar Incidence Model for Panel Data and Its Application

CUI Li-zhi1，LIU Si-feng2

(1.Business School, Anhui University of Technology, Maanshan 243032, China；2. Nanjing University of Aeronautics and Astronautics, Nanjing 211106, China)

Grey incidence analysis is an important part of grey system theory which is used to ascertain the relationship grade between an inflential factor and the major behaviour factor. However, most of grey incidence models are mainly applied to the field in which the operational behaviour factor and relational factor are the cross-sectional data or time series data in a given system. Therefore, the grey model on pannel data is worth exploring that is the asscociated content in this paper.According to the basic idea of grey incidence of grey system theory, the degree of relative closeness of the development rate and growth rate indexes between the relative factor matrices and characteristic behavior matrix of the system is measured from two dimensions of individual and time on the basis of the definition of the matrix sequence of a discrete data sequence. With the measurement of grey incidence degree, the grey matrix similar incidence model of panel data is put forward from the traditional vector space to the matrix space and its properties are discussed. Finally, CO2emission is taken as an example where the data of carbon dioxide has been calculated for six provinces by the IPCC method in 2006 and the other data are from the Statistical Yearbook. And a grey matrix similar incidence model is established by measuring the CO2emission in 2005—2012 of six provinces in the central region in China. The real example shows its simplification and practicability. The empirical results show that people may take some main factors into account to abate carbon dioxide emission which are an effective way to implement energy saving and carbon emission reduction. For example, the central region can appropriately control the population scale but also put intensive economic development way that guide residents to live low carbon and improve the consciousness of energy conservation and carbon emission reduction.

degree of grey matrix similar incidence; development speed index; growth index; carbon emission

2014-07-11；

2014-12-15

教育部人文社会科学研究青年基金资助项目(11YJC630034)；安徽省自然科学基金资助项目(1208085QG132)

崔立志(1978-)，男(汉族)，安徽庐江人，安徽工业大学商学院博士，副教授，研究方向：灰色系统理论、数量经济学.

1003-207(2015)11-0171-06

10.16381/j.cnki.issn1003-207x.2015.11.021

N94

A